Class octonion

• Acknowledgements
• Header File
• Test Program
• Synopsis
• Template class octonion
• octonion specializations
• octonion member functions
• octonion member operators
• octonion non-member operations
• octonion value operations
• octonion transcendentals
• History
• To Do

Octonions, like quaternions, are a relative of complex numbers.

Octonions see some use in theoretical physics.

In practical terms, an octonion is simply an octuple of real numbers , which we can write in the form , where , and are the same objects as for quaternions, and , , and are distinct objects which play essentially the same kind of role as (or or ).

An addition and a multiplication is defined on the set of octonions, which generalize their quaternionic counterparts. The main novelty this time is that the multiplication is not only not commutative, is now not even associative (i.e. there are quaternions , and such that ). A way of remembering things is by using the following multiplication table:

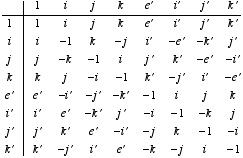
Octonions (and their kin) are described in far more details in this other document (with errata and addenda).

Some traditional constructs, such as the exponential, carry over without too much change into the realms of octonions, but other, such as taking a square root, do not (the fact that the exponential has a closed form is a result of the author, but the fact that the exponential exists at all for octonions is known since quite a long time ago).

Acknowledgements

The mathematical text has been typeset with Nisus Writer. Jens Maurer has helped with portability and standard adherence, and was the Review Manager for this library. More acknowledgements in the History section. Thank you to all who contributed to the discution about this library.

Header File

The interface and implementation are both supplied by the header file octonion.h.

Test Program

The octonion_test.cpp test program tests octonions specialisations for float, double and long double (sample output).

If you define the symbol BOOST_OCTONION_TEST_VERBOSE, you will get additional output (verbose output); this will only be helpfull if you enable message output at the same time, of course (by uncommenting the relevant line in the test or by adding --log_level=messages to your command line,...). In that case, and if you are running interactively, you may in addition define the symbol BOOST_INTERACTIVE_TEST_INPUT_ITERATOR to interactively test the input operator with input of your choice from the standard input (instead of hard-coding it in the test).

Synopsis

namespace boost
{
	namespace math
	{
		
		template<typename T> class octonion;
		template<>           class octonion<float>;
		template<>           class octonion<double>; 
		template<>           class octonion<long double>; 
		
		// operators
		
		template<typename T> inline octonion<T> operator + (T const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator + (octonion<T> const & lhs, T const & rhs);
		template<typename T> inline octonion<T> operator + (::std::complex<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator + (octonion<T> const & lhs, ::std::complex<T> const & rhs);
		template<typename T> inline octonion<T> operator + (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator + (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
		template<typename T> inline octonion<T> operator + (octonion<T> const & lhs, octonion<T> const & rhs);
		
		template<typename T> inline octonion<T> operator - (T const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator - (octonion<T> const & lhs, T const & rhs);
		template<typename T> inline octonion<T> operator - (::std::complex<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator - (octonion<T> const & lhs, ::std::complex<T> const & rhs);
		template<typename T> inline octonion<T> operator - (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator - (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
		template<typename T> inline octonion<T> operator - (octonion<T> const & lhs, octonion<T> const & rhs);
		
		template<typename T> inline octonion<T> operator * (T const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator * (octonion<T> const & lhs, T const & rhs);
		template<typename T> inline octonion<T> operator * (::std::complex<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator * (octonion<T> const & lhs, ::std::complex<T> const & rhs);
		template<typename T> inline octonion<T> operator * (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator * (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
		template<typename T> inline octonion<T> operator * (octonion<T> const & lhs, octonion<T> const & rhs);
		
		template<typename T> inline octonion<T> operator / (T const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator / (octonion<T> const & lhs, T const & rhs);
		template<typename T> inline octonion<T> operator / (::std::complex<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator / (octonion<T> const & lhs, ::std::complex<T> const & rhs);
		template<typename T> inline octonion<T> operator / (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline octonion<T> operator / (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
		template<typename T> inline octonion<T> operator / (octonion<T> const & lhs, octonion<T> const & rhs); 
		
		template<typename T> inline octonion<T> operator + (octonion<T> const & o);
		template<typename T> inline octonion<T> operator - (octonion<T> const & o); 
		
		template<typename T> inline bool operator == (T const & lhs, octonion<T> const & rhs);
		template<typename T> inline bool operator == (octonion<T> const & lhs, T const & rhs);
		template<typename T> inline bool operator == (::std::complex<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline bool operator == (octonion<T> const & lhs, ::std::complex<T> const & rhs);
		template<typename T> inline bool operator == (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline bool operator == (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
		template<typename T> inline bool operator == (octonion<T> const & lhs, octonion<T> const & rhs);
		
		template<typename T> inline bool operator != (T const & lhs, octonion<T> const & rhs);
		template<typename T> inline bool operator != (octonion<T> const & lhs, T const & rhs);
		template<typename T> inline bool operator != (::std::complex<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline bool operator != (octonion<T> const & lhs, ::std::complex<T> const & rhs);
		template<typename T> inline bool operator != (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
		template<typename T> inline bool operator != (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
		template<typename T> inline bool operator != (octonion<T> const & lhs, octonion<T> const & rhs); 
		
		template<typename T, typename charT, class traits>
		::std::basic_istream<charT,traits> &	operator >> (::std::basic_istream<charT,traits> & is, octonion<T> & o);
		
		template<typename T, typename charT, class traits>
		::std::basic_ostream<charT,traits> &	operator << (::std::basic_ostream<charT,traits> & os, octonion<T> const & o);
		
		// values
		
		template<typename T>	inline T		real(octonion<T> const & o);
		template<typename T>	inline octonion<T>	unreal(octonion<T> const & o);
		
		template<typename T>	inline T		sup(octonion<T> const & o);
		template<typename T>	inline T		l1(octonion<T>const & o);	
		template<typename T>	inline T		abs(octonion<T> const & o);
		template<typename T>	inline T		norm(octonion<T>const  & o);
		template<typename T>	inline octonion<T>	conj(octonion<T> const & o);
		
		template<typename T>	inline octonion<T>	spherical(T const & rho, T const & theta, T const & phi1, T const & phi2, T const & phi3, T const & phi4, T const & phi5, T const & phi6);
		template<typename T>	inline octonion<T>	multipolar(T const & rho1, T const & theta1, T const & rho2, T const & theta2, T const & rho3, T const & theta3, T const & rho4, T const & theta4);
		template<typename T>	inline octonion<T>	cylindrical(T const & r, T const & angle, T const & h1, T const & h2, T const & h3, T const & h4, T const & h5, T const & h6);
		
		// transcendentals
		
		template<typename T>	inline octonion<T>	exp(octonion<T> const & o);
		template<typename T>	inline octonion<T>	cos(octonion<T> const & o);
		template<typename T>	inline octonion<T>	sin(octonion<T> const & o);
		template<typename T>	inline octonion<T>	tan(octonion<T> const & o);
		template<typename T>	inline octonion<T>	cosh(octonion<T> const & o);
		template<typename T>	inline octonion<T>	sinh(octonion<T> const & o);
		template<typename T>	inline octonion<T>	tanh(octonion<T> const & o);
		
		template<typename T>	octonion<T>		pow(octonion<T> const & o, int n);
		
	}
}

Template class octonion

namespace boost
{
	namespace math
	{
	
		template<typename T>
		class octonion
		{
		public:
			
			typedef T value_type;
			
			explicit		octonion(T const & requested_a = T(), T const & requested_b = T(), T const & requested_c = T(), T const & requested_d = T(), T const & requested_e = T(), T const & requested_f = T(), T const & requested_g = T(), T const & requested_h = T());
			explicit		octonion(::std::complex<T> const & z0, ::std::complex<T> const & z1 = ::std::complex<T>(), ::std::complex<T> const & z2 = ::std::complex<T>(), ::std::complex<T> const & z3 = ::std::complex<T>());
			explicit		octonion(::boost::math::quaternion<T> const & q0, ::boost::math::quaternion<T> const & q1 = ::boost::math::quaternion<T>());
			template<typename X> explicit	octonion(octonion<X> const & a_recopier);
			
			T			real() const;
			octonion<T>		unreal() const;
			
			T			R_component_1() const;
			T			R_component_2() const;
			T			R_component_3() const;
			T			R_component_4() const;
			T			R_component_5() const;
			T			R_component_6() const;
			T			R_component_7() const;
			T			R_component_8() const;
			
			::std::complex<T>	C_component_1() const;
			::std::complex<T>	C_component_2() const;
			::std::complex<T>	C_component_3() const;
			::std::complex<T>	C_component_4() const;
			
			::boost::math::quaternion<T>	H_component_1() const;
			::boost::math::quaternion<T>	H_component_2() const;
			
			octonion<T> &	operator = (octonion<T> const  & a_affecter);
			template<typename X>	octonion<T> &	operator = (octonion<X> const  & a_affecter);
			octonion<T> &	operator = (T const  & a_affecter);
			octonion<T> &	operator = (::std::complex<T> const & a_affecter);
			octonion<T> &	operator = (::boost::math::quaternion<T> const & a_affecter);
			
			octonion<T> &	operator += (T const & rhs);
			octonion<T> &	operator += (::std::complex<T> const & rhs);
			octonion<T> &	operator += (::boost::math::quaternion<T> const & rhs);
			template<typename X>	octonion<T> &	operator += (octonion<X> const & rhs);
			
			octonion<T> &	operator -= (T const & rhs);
			octonion<T> &	operator -= (::std::complex<T> const & rhs);
			octonion<T> &	operator -= (::boost::math::quaternion<T> const & rhs);
			template<typename X>	octonion<T> &	operator -= (octonion<X> const & rhs);
			
			octonion<T> &	operator *= (T const & rhs);
			octonion<T> &	operator *= (::std::complex<T> const & rhs);
			octonion<T> &	operator *= (::boost::math::quaternion<T> const & rhs);
			template<typename X>	octonion<T> &	operator *= (octonion<X> const & rhs);
			
			octonion<T> &	operator /= (T const & rhs);
			octonion<T> &	operator /= (::std::complex<T> const & rhs);
			octonion<T> &	operator /= (::boost::math::quaternion<T> const & rhs);
			template<typename X>	octonion<T> &	operator /= (octonion<X> const & rhs);
			
		};
		
	}
}

octonion specializations

namespace boost
{
	namespace math
	{
		
		template<>
		class octonion<float>
		{
		public:
			
			typedef float value_type;
			
			explicit		octonion(float const & requested_a = 0.0f, float const & requested_b = 0.0f, float const & requested_c = 0.0f, float const & requested_d = 0.0f, float const & requested_e = 0.0f, float const & requested_f = 0.0f, float const & requested_g = 0.0f, float const & requested_h = 0.0f);
			explicit		octonion(::std::complex<float> const & z0, ::std::complex<float> const & z1 = ::std::complex<float>(), ::std::complex<float> const & z2 = ::std::complex<float>(), ::std::complex<float> const & z3 = ::std::complex<float>());
			explicit		octonion(::boost::math::quaternion<float> const & q0, ::boost::math::quaternion<float> const & q1 = ::boost::math::quaternion<float>());
			explicit		octonion(octonion<double> const & a_recopier);
			explicit		octonion(octonion<long double> const & a_recopier);
			
			float			real() const;
			octonion<float>	unreal() const;
			
			float			R_component_1() const;
			float			R_component_2() const;
			float			R_component_3() const;
			float			R_component_4() const;
			float			R_component_5() const;
			float			R_component_6() const;
			float			R_component_7() const;
			float			R_component_8() const;
			
			::std::complex<float>	C_component_1() const;
			::std::complex<float>	C_component_2() const;
			::std::complex<float>	C_component_3() const;
			::std::complex<float>	C_component_4() const;
			
			::boost::math::octonion<float>	H_component_1() const;
			::boost::math::octonion<float>	H_component_2() const;
			
			octonion<float> &	operator = (octonion<float> const & a_affecter);
			template<typename X>	octonion<float> &	operator = (octonion<X>const  & a_affecter);
			octonion<float> &	operator = (float const & a_affecter);
			octonion<float> &	operator = (::std::complex<float> const & a_affecter);
			octonion<float> &	operator = (::boost::math::quaternion<float> const & a_affecter);
			
			octonion<float> &	operator += (float const & rhs);
			octonion<float> &	operator += (::std::complex<float> const & rhs);
			template<typename X>	octonion<float> &	operator += (octonion<X> const & rhs);
			
			octonion<float> &	operator -= (float const & rhs);
			octonion<float> &	operator -= (::std::complex<float> const & rhs);
			octonion<float> &	operator -= (::boost::math::quaternion<float> const & rhs);
			template<typename X>	octonion<float> &	operator -= (octonion<X> const & rhs);
			
			octonion<float> &	operator *= (float const & rhs);
			octonion<float> &	operator *= (::std::complex<float> const & rhs);
			octonion<float> &	operator *= (::boost::math::quaternion<float> const & rhs);
			template<typename X>	octonion<float> &	operator *= (octonion<X> const & rhs);
			
			octonion<float> &	operator /= (float const & rhs);
			octonion<float> &	operator /= (::std::complex<float> const & rhs);
			octonion<float> &	operator /= (::boost::math::quaternion<float> const & rhs);
			template<typename X>	octonion<float> &	operator /= (octonion<X> const & rhs);
		};
		
		
		template<>
		class octonion<double>
		{
		public:
			
			typedef double value_type;
			
			explicit		octonion(double const & requested_a = 0.0, double const & requested_b = 0.0, double const & requested_c = 0.0, double const & requested_d = 0.0, double const & requested_e = 0.0, double const & requested_f = 0.0, double const & requested_g = 0.0, double const & requested_h = 0.0);
			explicit		octonion(::std::complex<double> const & z0, ::std::complex<double> const & z1 = ::std::complex<double>(), ::std::complex<double> const & z2 = ::std::complex<double>(), ::std::complex<double> const & z3 = ::std::complex<double>());
			explicit		octonion(::boost::math::quaternion<double> const & q0, ::boost::math::quaternion<double> const & q1 = ::boost::math::quaternion<double>());
			explicit		octonion(octonion<float> const & a_recopier);
			explicit		octonion(octonion<long double> const & a_recopier);
			
			double			real() const;
			octonion<double>	unreal() const;
			
			double			R_component_1() const;
			double			R_component_2() const;
			double			R_component_3() const;
			double			R_component_4() const;
			double			R_component_5() const;
			double			R_component_6() const;
			double			R_component_7() const;
			double			R_component_8() const;
			
			::std::complex<double>	C_component_1() const;
			::std::complex<double>	C_component_2() const;
			::std::complex<double>	C_component_3() const;
			::std::complex<double>	C_component_4() const;
			
			::boost::math::quaternion<double>	H_component_1() const;
			::boost::math::quaternion<double>	H_component_2() const;
			
			octonion<double> &	operator = (octonion<double> const & a_affecter);
			template<typename X>	octonion<double> &	operator = (octonion<X> const & a_affecter);
			octonion<double> &	operator = (double const & a_affecter);
			octonion<double> &	operator = (::std::complex<double> const & a_affecter);
			octonion<double> &	operator = (::boost::math::quaternion<double> const & a_affecter);
			
			octonion<double> &	operator += (double const & rhs);
			octonion<double> &	operator += (::std::complex<double> const & rhs);
			octonion<double> &	operator += (::boost::math::quaternion<double> const & rhs);
			template<typename X> octonion<double> &	operator += (octonion<X> const & rhs);
			
			octonion<double> &	operator -= (double const & rhs);
			octonion<double> &	operator -= (::std::complex<double> const & rhs);
			octonion<double> &	operator -= (::boost::math::quaternion<double> const & rhs);
			template<typename X> octonion<double> &	operator -= (octonion<X> const & rhs);
			
			octonion<double> &	operator *= (double const & rhs);
			octonion<double> &	operator *= (::std::complex<double> const & rhs);
			octonion<double> &	operator *= (::boost::math::quaternion<double> const & rhs);
			template<typename X> octonion<double> &	operator *= (octonion<X> const & rhs);
			
			octonion<double> &	operator /= (double const & rhs);
			octonion<double> &	operator /= (::std::complex<double> const & rhs);
			octonion<double> &	operator /= (::boost::math::quaternion<double> const & rhs);
			template<typename X>	octonion<double> &	operator /= (octonion<X> const & rhs);
		};
		
		
		template<>
		class octonion<long double>
		{
		public:
			
			typedef long double value_type;
			
			explicit			octonion(long double const & requested_a = 0.0L, long double const & requested_b = 0.0L, long double const & requested_c = 0.0L, long double const & requested_d = 0.0L, long double const & requested_e = 0.0L, long double const & requested_f = 0.0L, long double const & requested_g = 0.0L, long double const & requested_h = 0.0L);
			explicit			octonion(	::std::complex<long double> const & z0, ::std::complex<long double> const & z1 = ::std::complex<long double>(), ::std::complex<long double> const & z2 = ::std::complex<long double>(), ::std::complex<long double> const & z3 = ::std::complex<long double>());
			explicit			octonion(	::boost::math::quaternion<long double> const & q0, ::boost::math::quaternion<long double> const & z1 = ::boost::math::quaternion<long double>());
			explicit			octonion(octonion<float> const & a_recopier);
			explicit			octonion(octonion<double> const & a_recopier);
			
			long double			real() const;
			octonion<long double>		unreal() const;
			
			long double			R_component_1() const;
			long double			R_component_2() const;
			long double			R_component_3() const;
			long double			R_component_4() const;
			long double			R_component_5() const;
			long double			R_component_6() const;
			long double			R_component_7() const;
			long double			R_component_8() const;
			
			::std::complex<long double>	C_component_1() const;
			::std::complex<long double>	C_component_2() const;
			::std::complex<long double>	C_component_3() const;
			::std::complex<long double>	C_component_4() const;
			
			::boost::math::quaternion<long double>	H_component_1() const;
			::boost::math::quaternion<long double>	H_component_2() const;
			
			octonion<long double> &	operator = (octonion<long double> const & a_affecter);
			template<typename X>	octonion<long double> &	operator = (octonion<X> const & a_affecter);
			octonion<long double> &	operator = (long double const & a_affecter);
			octonion<long double> &	operator = (::std::complex<long double> const & a_affecter);
			octonion<long double> &	operator = (::boost::math::quaternion<long double> const & a_affecter);
			
			octonion<long double> &	operator += (long double const & rhs);
			octonion<long double> &	operator += (::std::complex<long double> const & rhs);
			octonion<long double> &	operator += (::boost::math::quaternion<long double> const & rhs);
			template<typename X>	octonion<long double> &	operator += (octonion<X> const & rhs);
			
			octonion<long double> &	operator -= (long double const & rhs);
			octonion<long double> &	operator -= (::std::complex<long double> const & rhs);
			octonion<long double> &	operator -= (::boost::math::quaternion<long double> const & rhs);
			template<typename X>	octonion<long double> &	operator -= (octonion<X> const & rhs);
			
			octonion<long double> &	operator *= (long double const & rhs);
			octonion<long double> &	operator *= (::std::complex<long double> const & rhs);
			octonion<long double> &	operator *= (::boost::math::quaternion<long double> const & rhs);
			template<typename X>	octonion<long double> &	operator *= (octonion<X> const & rhs);
			
			octonion<long double> &	operator /= (long double const & rhs);
			octonion<long double> &	operator /= (::std::complex<long double> const & rhs);
			octonion<long double> &	operator /= (::boost::math::quaternion<long double> const & rhs);
			template<typename X>	octonion<long double> &	operator /= (octonion<X> const & rhs);
		};
		
	}
}

octonion typedefs

value_type

typedef T value_type;

Template version.

typedef float value_type;

Float specialization version.

typedef double value_type;

Double specialization version.

typedef long double value_type;

Long double specialization version.

These provide easy acces to the type the template is built upon.

octonion member functions

Constructors

explicit		octonion(T const & requested_a = T(), T const & requested_b = T(), T const & requested_c = T(), T const & requested_d = T(), T const & requested_e = T(), T const & requested_f = T(), T const & requested_g = T(), T const & requested_h = T());
explicit		octonion(::std::complex<T> const & z0, ::std::complex<T> const & z1 = ::std::complex<T>(), ::std::complex<T> const & z2 = ::std::complex<T>(), ::std::complex<T> const & z3 = ::std::complex<T>());
explicit		octonion(::boost::math::quaternion<T> const & q0, ::boost::math::quaternion<T> const & q1 = ::boost::math::quaternion<T>());
template<typename X> explicit	octonion(octonion<X> const & a_recopier);

Template version.

explicit		octonion(float const & requested_a = 0.0f, float const & requested_b = 0.0f, float const & requested_c = 0.0f, float const & requested_d = 0.0f, float const & requested_e = 0.0f, float const & requested_f = 0.0f, float const & requested_g = 0.0f, float const & requested_h = 0.0f);
explicit		octonion(::std::complex<float> const & z0, ::std::complex<float> const & z1 = ::std::complex<float>(), ::std::complex<float> const & z2 = ::std::complex<float>(), ::std::complex<float> const & z3 = ::std::complex<float>());
explicit		octonion(::boost::math::quaternion<float> const & q0, ::boost::math::quaternion<float> const & q1 = ::boost::math::quaternion<float>());
explicit		octonion(octonion<double> const & a_recopier); 
explicit		octonion(octonion<long double> const & a_recopier);

Float specialization version.

explicit		octonion(double const & requested_a = 0.0, double const & requested_b = 0.0, double const & requested_c = 0.0, double const & requested_d = 0.0, double const & requested_e = 0.0, double const & requested_f = 0.0, double const & requested_g = 0.0, double const & requested_h = 0.0);
explicit		octonion(::std::complex<double> const & z0, ::std::complex<double> const & z1 = ::std::complex<double>(), ::std::complex<double> const & z2 = ::std::complex<double>(), ::std::complex<double> const & z3 = ::std::complex<double>());
explicit		octonion(::boost::math::quaternion<double> const & q0, ::boost::math::quaternion<double> const & q1 = ::boost::math::quaternion<double>());
explicit		octonion(octonion<float> const & a_recopier);
explicit		octonion(octonion<long double> const & a_recopier);

Double specialization version.

explicit		octonion(long double const & requested_a = 0.0L, long double const & requested_b = 0.0L, long double const & requested_c = 0.0L, long double const & requested_d = 0.0L, long double const & requested_e = 0.0L, long double const & requested_f = 0.0L, long double const & requested_g = 0.0L, long double const & requested_h = 0.0L);
explicit		octonion(	::std::complex<long double> const & z0, ::std::complex<long double> const & z1 = ::std::complex<long double>(), ::std::complex<long double> const & z2 = ::std::complex<long double>(), ::std::complex<long double> const & z3 = ::std::complex<long double>());
explicit		octonion(::boost::math::quaternion<long double> const & q0, ::boost::math::quaternion<long double> const & q1 = ::boost::math::quaternion<long double>());
explicit		octonion(octonion<float> const & a_recopier);
explicit		octonion(octonion<double> const & a_recopier);

Long double specialization version.

A default constructor is provided for each form, which initializes each component to the default values for their type (i.e. zero for floating numbers). This constructor can also accept one to eight base type arguments. A constructor is also provided to build octonions from one to four complex numbers sharing the same base type, and another taking one or two quaternionssharing the same base type. The unspecialized template also sports a templarized copy constructor, while the specialized forms have copy constructors from the other two specializations, which are explicit when a risk of precision loss exists. For the unspecialized form, the base type's constructors must not throw.

Destructors and untemplated copy constructors (from the same type) are provided by the compiler. Converting copy constructors make use of a templated helper function in a "detail" subnamespace.

Other member functions

T			real() const;
octonion<T>		unreal() const;

Like complex number, octonions do have a meaningful notion of "real part", but unlike them there is no meaningful notion of "imaginary part". Instead there is an "unreal part" which itself is a octonion, and usually nothing simpler (as opposed to the complex number case). These are returned by the first two functions.

T			R_component_1() const;
T			R_component_2() const;
T			R_component_3() const;
T			R_component_4() const;
T			R_component_5() const;
T			R_component_6() const;
T			R_component_7() const;
T			R_component_8() const;

A octonion having eight real components, these are returned by these eight functions. Hence real and R_component_1 return the same value.

::std::complex<T>	C_component_1() const;
::std::complex<T>	C_component_2() const;
::std::complex<T>	C_component_3() const;
::std::complex<T>	C_component_4() const;

A octonion likewise has four complex components. Actually, octonions are indeed a (left) vector field over the complexes, but beware, as for any octonion we also have (note the minus sign in the last factor). What the C_component_n functions return, however, are the complexes which could be used to build the octonion using the constructor, and not the components of the octonion on the basis .

::boost::math::quaternion<T>	H_component_1() const;
::boost::math::quaternion<T>	H_component_2() const;

Likewise, for any octonion we also have , though there is no meaningful vector-space-like structure based on the quaternions. What the H_component_n functions return are the quaternions which could be used to build the octonion using the constructor.

octonion member operators

Assignment operators

octonion<T> & operator = (octonion<T> const & a_affecter);
template<typename X> octonion<T> & operator = (octonion<X> const & a_affecter);
octonion<T> & operator = (T const & a_affecter);
octonion<T> & operator = (::std::complex<T> const & a_affecter);
octonion<T> & operator = (::boost::math::quaternion<T> const & a_affecter);

These perform the expected assignment, with type modification if necessary (for instance, assigning from a base type will set the real part to that value, and all other components to zero). For the unspecialized form, the base type's assignment operators must not throw.

Other member operators

octonion<T> &	operator += (T const & rhs)
octonion<T> &	operator += (::std::complex<T> const & rhs);
octonion<T> &	operator += (::boost::math::quaternion<T> const & rhs);
template<typename X>	octonion<T> &	operator += (octonion<X> const & rhs);

These perform the mathematical operation (*this)+rhs and store the result in *this. The unspecialized form has exception guards, which the specialized forms do not, so as to insure exception safety. For the unspecialized form, the base type's assignment operators must not throw.

octonion<T> &	operator -= (T const & rhs)
octonion<T> &	operator -= (::std::complex<T> const & rhs);
octonion<T> &	operator -= (::boost::math::quaternion<T> const & rhs);
template<typename X>	octonion<T> &	operator -= (octonion<X> const & rhs);

These perform the mathematical operation (*this)-rhs and store the result in *this. The unspecialized form has exception guards, which the specialized forms do not, so as to insure exception safety. For the unspecialized form, the base type's assignment operators must not throw.

octonion<T> &	operator *= (T const & rhs)
octonion<T> &	operator *= (::std::complex<T> const & rhs);
octonion<T> &	operator *= (::boost::math::quaternion<T> const & rhs);
template<typename X>	octonion<T> &	operator *= (octonion<X> const & rhs);

These perform the mathematical operation (*this)*rhs in this order (order is important as multiplication is not commutative for octonions) and store the result in *this. The unspecialized form has exception guards, which the specialized forms do not, so as to insure exception safety. For the unspecialized form, the base type's assignment operators must not throw. Also, for clarity's sake, you should always group the factors in a multiplication by groups of two, as the multiplication is not even associative on the octonions (though there are of course cases where this does not matter, it usually does).

octonion<T> &	operator /= (T const & rhs)
octonion<T> &	operator /= (::std::complex<T> const & rhs);
octonion<T> &	operator /= (::boost::math::quaternion<T> const & rhs);
template<typename X>	octonion<T> &	operator /= (octonion<X> const & rhs);

These perform the mathematical operation (*this)*inverse_of(rhs) in this order (order is important as multiplication is not commutative for octonions) and store the result in *this. The unspecialized form has exception guards, which the specialized forms do not, so as to insure exception safety. For the unspecialized form, the base type's assignment operators must not throw. As for the multiplication, remember to group any two factors using parenthesis.

octonion non-member operations

template<typename T>	inline octonion<T>	operator + (octonion<T> const & o);

This unary operator simply returns o.

template<typename T>	inline octonion<T>	operator - (octonion<T> const & o);

This unary operator returns the opposite of o.

template<typename T>	inline octonion<T>	operator + (T const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator + (octonion<T> const & lhs, T const & rhs);
template<typename T>	inline octonion<T>	operator + (::std::complex<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator + (octonion<T> const & lhs, ::std::complex<T> const & rhs);
template<typename T>	inline octonion<T>	operator + (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator + (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
template<typename T>	inline octonion<T>	operator + (octonion<T> const & lhs, octonion<T> const & rhs);

These operators return octonion<T>(lhs) += rhs.

template<typename T>	inline octonion<T>	operator - (T const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator - (octonion<T> const & lhs, T const & rhs);
template<typename T>	inline octonion<T>	operator - (::std::complex<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator - (octonion<T> const & lhs, ::std::complex<T> const & rhs);
template<typename T>	inline octonion<T>	operator - (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator - (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
template<typename T>	inline octonion<T>	operator - (octonion<T> const & lhs, octonion<T> const & rhs);

These operators return octonion<T>(lhs) -= rhs.

template<typename T>	inline octonion<T>	operator * (T const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator * (octonion<T> const & lhs, T const & rhs);
template<typename T>	inline octonion<T>	operator * (::std::complex<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator * (octonion<T> const & lhs, ::std::complex<T> const & rhs);
template<typename T>	inline octonion<T>	operator * (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator * (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
template<typename T>	inline octonion<T>	operator * (octonion<T> const & lhs, octonion<T> const & rhs);

These operators return octonion<T>(lhs) *= rhs.

template<typename T>	inline octonion<T>	operator / (T const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator / (octonion<T> const & lhs, T const & rhs);
template<typename T>	inline octonion<T>	operator / (::std::complex<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator / (octonion<T> const & lhs, ::std::complex<T> const & rhs);
template<typename T>	inline octonion<T>	operator / (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline octonion<T>	operator / (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
template<typename T>	inline octonion<T>	operator / (octonion<T> const & lhs, octonion<T> const & rhs);

These operators return octonion<T>(lhs) /= rhs. It is of course still an error to divide by zero...

template<typename T>	inline bool	operator == (T const & lhs, octonion<T> const & rhs);
template<typename T>	inline bool	operator == (octonion<T> const & lhs, T const & rhs);
template<typename T>	inline bool	operator == (::std::complex<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline bool	operator == (octonion<T> const & lhs, ::std::complex<T> const & rhs);
template<typename T>	inline bool	operator == (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline bool	operator == (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
template<typename T>	inline bool	operator == (octonion<T> const & lhs, octonion<T> const & rhs);

These return true if and only if the four components of octonion<T>(lhs) are equal to their counterparts in octonion<T>(rhs). As with any floating-type entity, this is essentially meaningless.

template<typename T>	inline bool	operator != (T const & lhs, octonion<T> const & rhs);
template<typename T>	inline bool	operator != (octonion<T> const & lhs, T const & rhs);
template<typename T>	inline bool	operator != (::std::complex<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline bool	operator != (octonion<T> const & lhs, ::std::complex<T> const & rhs);
template<typename T>	inline bool	operator != (::boost::math::quaternion<T> const & lhs, octonion<T> const & rhs);
template<typename T>	inline bool	operator != (octonion<T> const & lhs, ::boost::math::quaternion<T> const & rhs);
template<typename T>	inline bool	operator != (octonion<T> const & lhs, octonion<T> const & rhs);

These return true if and only if octonion<T>(lhs) == octonion<T>(rhs) is false. As with any floating-type entity, this is essentially meaningless.

template<typename T, typename charT, class traits>
::std::basic_istream<charT,traits> &	operator >> (::std::basic_istream<charT,traits> & is, octonion<T> & o);

Extracts an octonion o. We accept any format which seems reasonable. However, since this leads to a great many ambiguities, decisions were made to lift these. In case of doubt, stick to lists of reals.

The input values must be convertible to T. If bad input is encountered, calls is.setstate(ios::failbit) (which may throw ios::failure (27.4.5.3)).

Returns is.

template<typename T, typename charT, class traits>
::std::basic_ostream<charT,traits> &	operator << (::std::basic_ostream<charT,traits> & os, octonion<T> const & o);

Inserts the octonion o onto the stream os as if it were implemented as follows:

	template<typename T, typename charT, class traits>
	::std::basic_ostream<charT,traits> &	operator << (	::std::basic_ostream<charT,traits> & os,
								octonion<T> const & o)
					{
						::std::basic_ostringstream<charT,traits>	s;
						
						s.flags(os.flags());
						s.imbue(os.getloc());
						s.precision(os.precision());
						
						s << '('	<< o.R_component_1() << ','
								<< o.R_component_2() << ','
								<< o.R_component_3() << ','
								<< o.R_component_4() << ','
								<< o.R_component_5() << ','
								<< o.R_component_6() << ','
								<< o.R_component_7() << ','
								<< o.R_component_8() << ')';
									
						return os << s.str();
					}

octonion value operations

template<typename T>	inline T		real(octonion<T> const & o);
template<typename T>	inline octonion<T>	unreal(octonion<T> const & o);

These return o.real() and o.unreal() respectively.

template<typename T>	inline octonion<T>	conj(octonion<T> const & o);

This returns the conjugate of the octonion.

template<typename T>	inline T	 	sup(octonion<T> const & o);

This return the sup norm (the greatest among abs(o.R_component_1())...abs(o.R_component_8())) of the octonion.

template<typename T>	inline T	 	l1(octonion<T> const & o);

This return the l1 norm (abs(o.R_component_1())+...+abs(o.R_component_8())) of the octonion.

template<typename T>	inline T	 	abs(octonion<T> const & o);

This return the magnitude (Euclidian norm) of the octonion.

template<typename T>	inline T		norm(octonion<T>const  & o);

This return the (Cayley) norm of the octonion. The term "norm" might be confusing, as most people associate it with the Euclidian norm (and quadratic functionals). For this version of (the mathematical objects known as) octonions, the Euclidian norm (also known as magnitude) is the square root of the Cayley norm.

template<typename T>	inline octonion<T>	spherical(T const & rho, T const & theta, T const & phi1, T const & phi2, T const & phi3, T const & phi4, T const & phi5, T const & phi6);
template<typename T>	inline octonion<T>	multipolar(T const & rho1, T const & theta1, T const & rho2, T const & theta2, T const & rho3, T const & theta3, T const & rho4, T const & theta4);
template<typename T>	inline octonion<T>	cylindrical(T const & r, T const & angle, T const & h1, T const & h2, T const & h3, T const & h4, T const & h5, T const & h6);

These build octonions in a way similar to the way polar builds complex numbers, as there is no strict equivalent to polar coordinates for octonions.

spherical is a simple transposition of polar, it takes as inputs a (positive) magnitude and a point on the hypersphere, given by three angles. The first of these, theta has a natural range of -pi to +pi, and the other two have natural ranges of -pi/2 to +pi/2 (as is the case with the usual spherical coordinates in R^3). Due to the many symmetries and periodicities, nothing untoward happens if the magnitude is negative or the angles are outside their natural ranges. The expected degeneracies (a magnitude of zero ignores the angles settings...) do happen however.

cylindrical is likewise a simple transposition of the usual cylindrical coordinates in R^3, which in turn is another derivative of planar polar coordinates. The first two inputs are the polar coordinates of the first C component of the octonion. The third and fourth inputs are placed into the third and fourth R components of the octonion, respectively.

multipolar is yet another simple generalization of polar coordinates. This time, both C components of the octonion are given in polar coordinates.

In this version of our implementation of octonions, there is no analogue of the complex value operation arg as the situation is somewhat more complicated.

octonion transcendentals

There is no log or sqrt provided for octonions in this implementation, and pow is likewise restricted to integral powers of the exponent. There are several reasons to this: on the one hand, the equivalent of analytic continuation for octonions ("branch cuts") remains to be investigated thoroughly (by me, at any rate...), and we wish to avoid the nonsense introduced in the standard by exponentiations of complexes by complexes (which is well defined, but not in the standard...). Talking of nonsense, saying that pow(0,0) is "implementation defined" is just plain brain-dead...

We do, however provide several transcendentals, chief among which is the exponential. That it allows for a "closed formula" is a result of the author (the existence and definition of the exponential, on the octonions among others, on the other hand, is a few centuries old). Basically, any converging power series with real coefficients which allows for a closed formula in C can be transposed to O. More transcendentals of this type could be added in a further revision upon request. It should be noted that it is these functions which force the dependency upon the boost/math/special_functions/sinc.hpp and the boost/math/special_functions/sinhc.hpp headers.

exp

template<typename T>	inline octonion<T>	exp(octonion<T> const & o);

Computes the exponential of the octonion.

cos

template<typename T>	inline octonion<T>	cos(octonion<T> const & o);

Computes the cosine of the octonion

sin

template<typename T>	inline octonion<T>	sin(octonion<T> const & o);

Computes the sine of the octonion.

tan

template<typename T>	inline octonion<T>	tan(octonion<T> const & o);

Computes the tangent of the octonion.

cosh

template<typename T>	inline octonion<T>	cosh(octonion<T> const & o);

Computes the hyperbolic cosine of the octonion.

sinh

template<typename T>	inline octonion<T>	sinh(octonion<T> const & o);

Computes the hyperbolic sine of the octonion.

tanh

template<typename T>	inline octonion<T>	tanh(octonion<T> const & o);

Computes the hyperbolic tangent of the octonion.

pow

template<typename T>	octonion<T>		pow(octonion<T> const & o, int n);

Computes the n-th power of the octonion q.

History

• 1.5.7 - 25/02/2003: transitionned to the unit test framework; <boost/config.hpp> now included by the library header (rather than the test files), via <boost/math/quaternion.hpp>.
• 1.5.6 - 15/10/2002: Gcc2.95.x and stlport on linux compatibility by Alkis Evlogimenos ([email protected]).
• 1.5.5 - 27/09/2002: Microsoft VCPP 7 compatibility, by Michael Stevens ([email protected]); requires the /Za compiler option.
• 1.5.4 - 19/09/2002: fixed problem with multiple inclusion (in different translation units); attempt at an improved compatibility with Microsoft compilers, by Michael Stevens ([email protected]) and Fredrik Blomqvist; other compatibility fixes.
• 1.5.3 - 01/02/2002: bugfix and Gcc 2.95.3 compatibility by Douglas Gregor ([email protected]).
• 1.5.2 - 07/07/2001: introduced namespace math.
• 1.5.1 - 07/06/2001: (end of Boost review) now includes <boost/math/special_functions/sinc.hpp> and <boost/math/special_functions/sinhc.hpp> instead of <boost/special_functions.hpp>; corrected bug in sin (Daryle Walker); removed check for self-assignment (Gary Powel); made converting functions explicit (Gary Powel); added overflow guards for division operators and abs (Peter Schmitteckert); added sup and l1; used Vesa Karvonen's CPP metaprograming technique to simplify code.
• 1.5.0 - 23/03/2001: boostification, inlining of all operators except input, output and pow, fixed exception safety of some members (template version).
• 1.4.0 - 09/01/2001: added tan and tanh.
• 1.3.1 - 08/01/2001: cosmetic fixes.
• 1.3.0 - 12/07/2000: pow now uses Maarten Hilferink's ([email protected]) algorithm.
• 1.2.0 - 25/05/2000: fixed the division operators and output; changed many signatures.
• 1.1.0 - 23/05/2000: changed sinc into sinc_pi; added sin, cos, sinh, cosh.
• 1.0.0 - 10/08/1999: first public version.

To Do

• Improve testing.
• Rewrite input operatore using Spirit (creates a dependency).
• Put in place an Expression Template mechanism (perhaps borrowing from uBlas).

Revised 25 Feb 2003

© Copyright Hubert Holin 2001-2003. Permission to copy, use, modify, sell and distribute this document is granted provided this copyright notice appears in all copies. This software is provided "as is" without express or implied  warranty, and with no claim as to its suitability for any purpose.