Public-key algorithms are asymmetric algorithms and, therefore, are based on the use of two different keys, instead of just one. In public-key cryptography, the two keys are called the private key and the public key
Private key: This key must be know only by its owner.
Public key: This key is known to everyone (it is public)
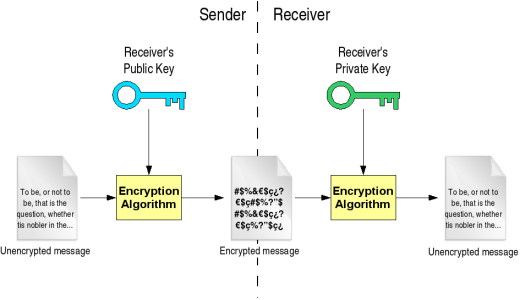
Relation between both keys: What one key encrypts, the other one decrypts, and vice versa. That means that if you encrypt something with my public key (which you would know, because it's public :-), I would need my private key to decrypt the message.
In a basic secure conversation using public-key cryptography, the sender encrypts the message using the receiver's public key. Remember that this key is known to everyone. The encrypted message is sent to the receiving end, who will decrypt the message with his private key. Only the receiver can decrypt the message because no one else has the private key. Also, notice how the encryption algorithm is the same at both ends: what is encrypted with one key is decrypted with the other key using the same algorithm.
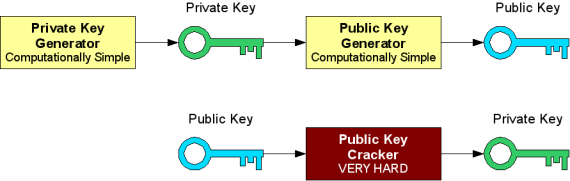
Public-key systems have a clear advantage over symmetric algorithms: there is no need to agree on a common key for both the sender and the receiver. As seen in the previous example, if someone wants to receive an encrypted message, the sender only needs to know the receiver's public key (which the receiver will provide; publishing the public key in no way compromises the secure transmission). As long as the receiver keeps the private key secret, no one but the receiver will be able to decrypt the messages encrypted with the corresponding public key. This is due to the fact that, in public-key systems, it is relatively easy to compute the public key from the private key, but very hard to compute the private key from the public key (which is the one everyone knows). In fact, some algorithms need several months (and even years) of constant computation to obtain the private key from the public key.
Another important advantage is that, unlike symmetric algorithms, public-key systems can guarantee integrity and authentication, not only privacy. The basic communication seen above only guarantees privacy. We will shortly see how integrity and authentication fit into public-key systems.
The main disadvantage of using public-key systems is that they are not as fast as symmetric algorithms.
Integrity is guaranteed in public-key systems by using digital signatures. A digital signature is a piece of data which is attached to a message and which can be used to find out if the message was tampered with during the conversation (e.g. through the intervention of a malicious user)
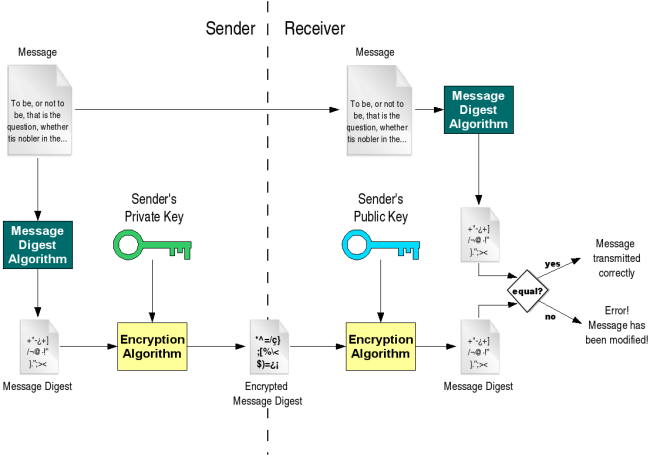
The digital signature for a message is generated in two steps:
A message digest is generated. A message digest is a 'summary' of the message we are going to transmit, and has two important properties: (1) It is always smaller than the message itself and (2) Even the slightest change in the message produces a different digest. The message digest is generated using a set of hashing algorithms.
The message digest is encrypted using the sender's private key. The resulting encrypted message digest is the digital signature.
The digital signature is attached to the message, and sent to the receiver. The receiver then does the following:
Using the sender's public key, decrypts the digital signature to obtain the message digest generated by the sender.
Uses the same message digest algorithm used by the sender to generate a message digest of the received message.
Compares both message digests (the one sent by the sender as a digital signature, and the one generated by the receiver). If they are not exactly the same, the message has been tampered with by a third party. We can be sure that the digital signature was sent by the sender (and not by a malicious user) because only the sender's public key can decrypt the digital signature (which was encrypted by the sender's private key; remember that what one key encrypts, the other one decrypts, and vice versa). If decrypting using the public key renders a faulty message digest, this means that either the message or the message digest are not exactly what the sender sent.
Using public-key cryptography in this manner ensures integrity, because we have a way of knowing if the message we received is exactly what was sent by the sender. However, notice how the above example guarantees only integrity. The message itself is sent unencrypted. This is not necessarily a bad thing: in some cases we might not be interested in keeping the data private, we simply want to make sure it isn't tampered with. To add privacy to this conversation, we would simply need to encrypt the message as explained in the first diagram.
The above example does guarantee, to a certain extent, the authenticity of the sender. Since only the sender's public key can decrypt the digital signature (encrypted with the sender's private key). However, the only thing this guarantees is that whoever sent the message has the private key corresponding to the public key we used to decrypt the digital signature. Although this public key might have been advertised as belonging to the sender, how can we be absolutely certain? Maybe the sender isn't really who he claims to be, but just someone impersonating the sender.
Some security scenarios might consider that the 'weak authentication' shown in the previous example is sufficient. However, other scenarios might require that there is absolutely no doubt about a user's identity. This is achieved with digital certificates, which are explained in the next page.