Natural Language Processing
| Authors: | Steven Bird, Ewan Klein, Edward Loper |
|---|---|
| Version: | 0.9.5 (draft only, please send feedback to authors) |
| Copyright: | © 2001-2008 the authors |
| License: | Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License |
| Revision: | |
| Date: |
Contents
- Preface
- 1. Introduction to Natural Language Processing and Python
- 2. Words: The Building Blocks of Language
- 3. Categorizing and Tagging Words
- 4. Data-Intensive Language Processing
- 5. Structured Programming in Python
- 6. Partial Parsing and Interpretation
- 7. Context Free Grammars and Parsing
- 8. Chart Parsing and Probabilistic Parsing
- 9. Applied Programming in Python
- 10. Feature Based Grammar
- 11. Logical Semantics
- 12. Linguistic Data Management (DRAFT)
- 13. Conclusion
- Appendix: Regular Expressions
- Appendix: Text Processing with Unicode
- Appendix: NLP in Python vs other Programming Languages
- Appendix: NLTK Modules and Corpora
- Appendix: Python and NLTK Cheat Sheet (Draft)
Preface
This is a book about Natural Language Processing. By natural language we mean a language that is used for everyday communication by humans; languages like English, Hindi or Portuguese. In contrast to artificial languages such as programming languages and logical formalisms, natural languages have evolved as they pass from generation to generation, and are hard to pin down with explicit rules. We will take Natural Language Processing (or NLP for short) in a wide sense to cover any kind of computer manipulation of natural language. At one extreme, it could be as simple as counting the number of times the letter t occurs in a paragraph of text. At the other extreme, NLP might involve "understanding" complete human utterances, at least to the extent of being able to give useful responses to them.
Most human knowledge — and most human communication — is represented and expressed using language. Technologies based on NLP are becoming increasingly widespread. For example, handheld computers (PDAs) support predictive text and handwriting recognition; web search engines give access to information locked up in unstructured text; machine translation allows us to retrieve texts written in Chinese and read them in Spanish. By providing more natural human-machine interfaces, and more sophisticated access to stored information, language processing has come to play a central role in the multilingual information society.
This book provides a comprehensive introduction to the field of NLP. It can be used for individual study or as the textbook a course on natural language processing or computational linguistics. The book is intensely practical, containing hundreds of fully-worked examples and graded exercises. It is based on the Python programming language together with an open source library called the Natural Language Toolkit NLTK. NLTK includes software, data, and documentation, all freely downloadable from http://nltk.org/. Distributions are provided for Windows, Macintosh and Unix platforms. We encourage you, the reader, to download Python and NLTK, and try out the examples and exercises along the way.
Audience
This book is intended for a diverse range of people who want to learn how to write programs that analyze written language:
| New to Programming?: | |
|---|---|
| The book is suitable for readers with no prior knowledge of programming, and the early chapters contain many examples that you can simply copy and try for yourself, together with graded exercises. If you decide you need a more general introduction to Python, we recommend you read Learning Python (O'Reilly) in conjunction with this book. | |
| New to Python?: | Experienced programmers can quickly learn enough Python using this book to get immersed in natural language processing. All relevant Python features are carefully explained and exemplified, and you will quickly come to appreciate Python's suitability for this application area. |
| Already dreaming in Python?: | |
| Simply skip the Python introduction, and dig into the interesting language analysis material that starts in Chapter 2. Soon you'll be applying your skills to this exciting new application area. | |
Emphasis
This book is a practical introduction to NLP. You will learn by example, write real programs, and grasp the value of being able to test an idea through implementation. If you haven't learnt already, this book will teach you programming. Unlike other programming books, we provide extensive illustrations and exercises from NLP. The approach we have taken is also principled, in that we cover the theoretical underpinnings and don't shy away from careful linguistic and computational analysis. We have tried to be pragmatic in striking a balance between theory and application, and alternate between the two several times each chapter, identifying the connections but also the tensions. Finally, we recognize that you won't get through this unless it is also pleasurable, so we have tried to include many applications and examples that are interesting and entertaining, sometimes whimsical.
What You Will Learn
By digging into the material presented here, you will learn:
- how simple programs can help you manipulate and analyze language data, and how to write these programs;
- how key concepts from NLP and linguistics are used to describe and analyse language;
- how data structures and algorithms are used in NLP;
- how language data is stored in standard formats, and how data can be used to evaluate the performance of NLP techniques.
Depending on your background, and your motivation for being interested in NLP, you will gain different kinds of skills and knowledge from this book, as set out below:
| Goals | Background | |
| Arts and Humanities | Science and Engineering | |
| Language Analysis | Programming to manage language data, explore linguistic models, and test empirical claims | Language as a source of interesting problems in data modeling, data mining, and knowledge discovery |
| Language Technology | Learning to program, with applications to familiar problems, to work in language technology or other technical field | Knowledge of linguistic algorithms and data structures for high quality, maintainable language processing software |
Organization
The book is structured into three parts, as follows:
- Part 1: Basics
- In this part, we focus on processing text, recognizing and categorizing words, and how to deal with large amounts of language data.
- Part 2: Parsing
- Here, we deal with grammatical structure in text: how words combine to make phrases and sentences, and how to automatically parse text into such structures.
- Part 3: Advanced Topics
- This final part of the book contains chapters that address selected topics in NLP in more depth and to a more advanced level. By design, the chapters in this part can be read independently of each other.
The three parts have a common structure: they start off with a chapter on programming, followed by three chapters on various topics in NLP. The programming chapters are foundational, and you must master this material before progressing further.
Each chapter consists of an introduction, a sequence of sections that progress from elementary to advanced material, and finally a summary and suggestions for further reading. Most sections include exercises that are graded according to the following scheme: ☼ is for easy exercises that involve minor modifications to supplied code samples or other simple activities; ◑ is for intermediate exercises that explore an aspect of the material in more depth, requiring careful analysis and design; ★ is for difficult, open-ended tasks that will challenge your understanding of the material and force you to think independently (readers new to programming are encouraged to skip these); ☺ is for non-programming exercises for reflection or discussion. The exercises are important for consolidating the material in each section, and we strongly encourage you to try a few before continuing with the rest of the chapter.
Why Python?
Python is a simple yet powerful programming language with excellent functionality for processing linguistic data. Python can be downloaded for free from http://www.python.org/.
Here is a five-line Python program that takes text input and prints all the words ending in ing:
|
This program illustrates some of the main features of Python. First, whitespace is used to nest lines of code, thus the line starting with if falls inside the scope of the previous line starting with for; this ensures that the ing test is performed for each word. Second, Python is object-oriented; each variable is an entity that has certain defined attributes and methods. For example, the value of the variable line is more than a sequence of characters. It is a string object that has a method (or operation) called split() that we can use to break a line into its words. To apply a method to an object, we write the object name, followed by a period, followed by the method name; i.e., line.split(). Third, methods have arguments expressed inside parentheses. For instance, in the example above, split() had no argument because we were splitting the string wherever there was white space, and we could therefore use empty parentheses. To split a string into sentences delimited by a period, we would write split('.'). Finally, and most importantly, Python is highly readable, so much so that it is fairly easy to guess what the above program does even if you have never written a program before.
We chose Python because it has a shallow learning curve, its syntax and semantics are transparent, and it has good string-handling functionality. As a scripting language, Python facilitates interactive exploration. As an object-oriented language, Python permits data and methods to be encapsulated and re-used easily. As a dynamic language, Python permits attributes to be added to objects on the fly, and permits variables to be typed dynamically, facilitating rapid development. Python comes with an extensive standard library, including components for graphical programming, numerical processing, and web data processing.
Python is heavily used in industry, scientific research, and education around the world. Python is often praised for the way it facilitates productivity, quality, and maintainability of software. A collection of Python success stories is posted at http://www.python.org/about/success/.
NLTK defines an infrastructure that can be used to build NLP programs in Python. It provides basic classes for representing data relevant to natural language processing; standard interfaces for performing tasks such as word tokenization, part-of-speech tagging, and syntactic parsing; and standard implementations for each task which can be combined to solve complex problems.
NLTK comes with extensive documentation. In addition to the book you are reading right now, the website http://nltk.org/ provides API documentation which covers every module, class and function in the toolkit, specifying parameters and giving examples of usage. The website also provides module guides; these contain extensive examples and test cases, and are intended for users, developers and instructors.
Learning Python for Natural Language Processing
This book contains self-paced learning materials including many examples and exercises. An effective way to learn is simply to work through the materials. The program fragments can be copied directly into a Python interactive session. Any questions concerning the book, or Python and NLP more generally, can be posted to the NLTK-Users mailing list (see http://nltk.org/).
| Python Environments: | |
|---|---|
| The easiest way to start developing Python code, and to run interactive Python demonstrations, is to use the simple editor and interpreter GUI that comes with Python called IDLE, the Integrated DeveLopment Environment for Python. | |
| NLTK Community: | NLTK has a large and growing user base. There are mailing lists for announcements about NLTK, for developers and for teachers. http://nltk.org/ lists many courses around the world where NLTK and materials from this book have been adopted, a useful source of extra materials including slides and exercises. |
The Design of NLTK
NLTK was designed with four primary goals in mind:
| Simplicity: | We have tried to provide an intuitive and appealing framework along with substantial building blocks, so you can gain a practical knowledge of NLP without getting bogged down in the tedious house-keeping usually associated with processing annotated language data. We have provided software distributions for several platforms, along with platform-specific instructions, to make the toolkit easy to install. |
|---|---|
| Consistency: | We have made a significant effort to ensure that all the data structures and interfaces are consistent, making it easy to carry out a variety of tasks using a uniform framework. |
| Extensibility: | The toolkit easily accommodates new components, whether those components replicate or extend existing functionality. Moreover, the toolkit is organized so that it is usually obvious where extensions would fit into the toolkit's infrastructure. |
| Modularity: | The interaction between different components of the toolkit uses simple, well-defined interfaces. It is possible to complete individual projects using small parts of the toolkit, without needing to understand how they interact with the rest of the toolkit. This allows students to learn how to use the toolkit incrementally throughout a course. Modularity also makes it easier to change and extend the toolkit. |
Contrasting with these goals are three non-requirements — potentially useful features that we have deliberately avoided. First, while the toolkit provides a wide range of functions, it is not intended to be encyclopedic; there should be a wide variety of ways in which students can extend the toolkit. Second, while the toolkit should be efficient enough that students can use their NLP systems to perform meaningful tasks, it does not need to be highly optimized for runtime performance; such optimizations often involve more complex algorithms, and sometimes require the use of programming languages like C or C++. This would make the toolkit less accessible and more difficult to install. Third, we have tried to avoid clever programming tricks, since clear implementations are preferable to ingenious yet indecipherable ones.
For Instructors
Natural Language Processing (NLP) is often taught within the confines of a single-semester course at advanced undergraduate level or postgraduate level. Many instructors have found that it is difficult to cover both the theoretical and practical sides of the subject in such a short span of time. Some courses focus on theory to the exclusion of practical exercises, and deprive students of the challenge and excitement of writing programs to automatically process language. Other courses are simply designed to teach programming for linguists, and do not manage to cover any significant NLP content. NLTK was originally developed to address this problem, making it feasible to cover a substantial amount of theory and practice within a single-semester course, even if students have no prior programming experience.
A significant fraction of any NLP syllabus deals with algorithms and data structures. On their own these can be rather dry, but NLTK brings them to life with the help of interactive graphical user interfaces making it possible to view algorithms step-by-step. Most NLTK components include a demonstration which performs an interesting task without requiring any special input from the user. An effective way to deliver the materials is through interactive presentation of the examples, entering them in a Python session, observing what they do, and modifying them to explore some empirical or theoretical issue.
The book contains hundreds of examples and exercises which can be used as the basis for student assignments. The simplest exercises involve modifying a supplied program fragment in a specified way in order to answer a concrete question. At the other end of the spectrum, NLTK provides a flexible framework for graduate-level research projects, with standard implementations of all the basic data structures and algorithms, interfaces to dozens of widely used data-sets (corpora), and a flexible and extensible architecture.
We believe this book is unique in providing a comprehensive framework for students to learn about NLP in the context of learning to program. What sets these materials apart is the tight coupling of the chapters and exercises with NLTK, giving students — even those with no prior programming experience — a practical introduction to NLP. Once completing these materials, students will be ready to attempt one of the more advanced textbooks, such as Speech and Language Processing, by Jurafsky and Martin (Prentice Hall, 2008).
| Suggested Course Plans; Lectures/Lab Sessions per Chapter | ||
|---|---|---|
| Chapter | Linguists | Computer Scientists |
| 1 Introduction | 1 | 1 |
| 2 Programming | 4 | 1 |
| 3 Words | 2-3 | 2 |
| 4 Tagging | 2 | 2 |
| 5 Data-Intensive Language Processing | 0-2 | 2 |
| 6 Structured Programming | 2-4 | 1 |
| 7 Chunking | 2 | 2 |
| 8 Grammars and Parsing | 2-6 | 2-4 |
| 9 Advanced Parsing | 1-4 | 3 |
| 10-14 Advanced Topics | 2-8 | 2-16 |
| Total | 18-36 | 18-36 |
Acknowledgments
NLTK was originally created as part of a computational linguistics course in the Department of Computer and Information Science at the University of Pennsylvania in 2001. Since then it has been developed and expanded with the help of dozens of contributors. It has now been adopted in courses in dozens of universities, and serves as the basis of many research projects.
In particular, we're grateful to the following people for their feedback, comments on earlier drafts, advice, contributions: Michaela Atterer, Greg Aumann, Kenneth Beesley, Ondrej Bojar, Trevor Cohn, Grev Corbett, James Curran, Jean Mark Gawron, Baden Hughes, Gwillim Law, Mark Liberman, Christopher Maloof, Stefan Müller, Stuart Robinson, Jussi Salmela, Rob Speer. Many others have contributed to the toolkit, and they are listed at http://nltk.org/. We are grateful to many colleagues and students for feedback on the text.
We are grateful to the US National Science Foundation, the Linguistic Data Consortium, and the Universities of Pennsylvania, Edinburgh, and Melbourne for supporting our work on this book.
About the Authors

Figure I.1: Edward Loper, Ewan Klein, and Steven Bird, Stanford, July 2007
Steven Bird is Associate Professor in the Department of Computer Science and Software Engineering at the University of Melbourne, and Senior Research Associate in the Linguistic Data Consortium at the University of Pennsylvania. After completing his undergraduate training in computer science and mathematics at the University of Melbourne, Steven went to the University of Edinburgh to study computational linguistics, and completed his PhD in 1990 under the supervision of Ewan Klein. He later moved to Cameroon to conduct linguistic fieldwork on the Grassfields Bantu languages. More recently, he spent several years as Associate Director of the Linguistic Data Consortium where he led an R&D team to create models and tools for large databases of annotated text. Back at Melbourne University, he leads a language technology research group and lectures in algorithms and Python programming. Steven is Vice President of the Association for Computational Linguistics.
Ewan Klein is Professor of Language Technology in the School of Informatics at the University of Edinburgh. He completed a PhD on formal semantics at the University of Cambridge in 1978. After some years working at the Universities of Sussex and Newcastle upon Tyne, Ewan took up a teaching position at Edinburgh. He was involved in the establishment of Edinburgh's Language Technology Group 1993, and has been closely associated with it ever since. From 2000–2002, he took leave from the University to act as Research Manager for the Edinburgh-based Natural Language Research Group of Edify Corporation, Santa Clara, and was responsible for spoken dialogue processing. Ewan is a past President of the European Chapter of the Association for Computational Linguistics and was a founding member and Coordinator of the European Network of Excellence in Human Language Technologies (ELSNET). He has been involved in leading numerous academic-industrial collaborative projects, the most recent of which is a biological text mining initiative funded by ITI Life Sciences, Scotland, in collaboration with Cognia Corporation, NY.
Edward Loper is a doctoral student in the Department of Computer and Information Sciences at the University of Pennsylvania, conducting research on machine learning in natural language processing. Edward was a student in Steven's graduate course on computational linguistics in the fall of 2000, and went on to be a TA and share in the development of NLTK. In addition to NLTK, he has helped develop other major packages for documenting and testing Python software, epydoc and doctest.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
Introduction to Part I
Part I covers the linguistic and computational analysis of words. You will learn how to extract the words out of documents and text collections in multiple languages, automatically categorize them as nouns, verbs, etc, and access their meanings. Part I also introduces the required programming skills along with basic statistical methods.
1 Introduction to Natural Language Processing and Python
1.1 The Language Challenge
Today, people from all walks of life — including professionals, students, and the general population — are confronted by unprecedented volumes of information, the vast bulk of which is stored as unstructured text. In 2003, it was estimated that the annual production of books amounted to 8 Terabytes. (A Terabyte is 1,000 Gigabytes, i.e., equivalent to 1,000 pickup trucks filled with books.) It would take a human being about five years to read the new scientific material that is produced every 24 hours. Although these estimates are based on printed materials, increasingly the information is also available electronically. Indeed, there has been an explosion of text and multimedia content on the World Wide Web. For many people, a large and growing fraction of work and leisure time is spent navigating and accessing this universe of information.
The presence of so much text in electronic form is a huge challenge to NLP. Arguably, the only way for humans to cope with the information explosion is to exploit computational techniques that can sift through huge bodies of text.
Although existing search engines have been crucial to the growth and popularity of the Web, humans require skill, knowledge, and some luck, to extract answers to such questions as What tourist sites can I visit between Philadelphia and Pittsburgh on a limited budget? What do expert critics say about digital SLR cameras? What predictions about the steel market were made by credible commentators in the past week? Getting a computer to answer them automatically is a realistic long-term goal, but would involve a range of language processing tasks, including information extraction, inference, and summarization, and would need to be carried out on a scale and with a level of robustness that is still beyond our current capabilities.
1.1.1 The Richness of Language
Language is the chief manifestation of human intelligence. Through language we express basic needs and lofty aspirations, technical know-how and flights of fantasy. Ideas are shared over great separations of distance and time. The following samples from English illustrate the richness of language:
| (1) |
|
Thanks to this richness, the study of language is part of many disciplines outside of linguistics, including translation, literary criticism, philosophy, anthropology and psychology. Many less obvious disciplines investigate language use, such as law, hermeneutics, forensics, telephony, pedagogy, archaeology, cryptanalysis and speech pathology. Each applies distinct methodologies to gather observations, develop theories and test hypotheses. Yet all serve to deepen our understanding of language and of the intellect that is manifested in language.
The importance of language to science and the arts is matched in significance by the cultural treasure embodied in language. Each of the world's ~7,000 human languages is rich in unique respects, in its oral histories and creation legends, down to its grammatical constructions and its very words and their nuances of meaning. Threatened remnant cultures have words to distinguish plant subspecies according to therapeutic uses that are unknown to science. Languages evolve over time as they come into contact with each other and they provide a unique window onto human pre-history. Technological change gives rise to new words like blog and new morphemes like e- and cyber-. In many parts of the world, small linguistic variations from one town to the next add up to a completely different language in the space of a half-hour drive. For its breathtaking complexity and diversity, human language is as a colorful tapestry stretching through time and space.
1.1.2 The Promise of NLP
As we have seen, NLP is important for scientific, economic, social, and cultural reasons. NLP is experiencing rapid growth as its theories and methods are deployed in a variety of new language technologies. For this reason it is important for a wide range of people to have a working knowledge of NLP. Within industry, it includes people in human-computer interaction, business information analysis, and Web software development. Within academia, this includes people in areas from humanities computing and corpus linguistics through to computer science and artificial intelligence. We hope that you, a member of this diverse audience reading these materials, will come to appreciate the workings of this rapidly growing field of NLP and will apply its techniques in the solution of real-world problems.
This book presents a carefully-balanced selection of theoretical foundations and practical applications, and equips readers to work with large datasets, to create robust models of linguistic phenomena, and to deploy them in working language technologies. By integrating all of this into the Natural Language Toolkit (NLTK), we hope this book opens up the exciting endeavor of practical natural language processing to a broader audience than ever before.
The rest of this chapter provides a non-technical overview of Python and will cover the basic programming knowledge needed for the rest of the chapters in Part 1. It contains many examples and exercises; there is no better way to learn to program than to dive in and try these yourself. You should then feel confident in adapting the example for your own purposes. Before you know it you will be programming!
1.2 Computing with Language
As we will see, it is easy to get our hands on large quantities of text. What can we do with it, assuming we can write some simple programs? Here we will treat the text as data for the programs we write, programs that manipulate and analyze it in a variety of interesting ways. The first step is to get started with the Python interpreter.
1.2.1 Getting Started
One of the friendly things about Python is that it allows you to type directly into the interactive interpreter — the program that will be running your Python programs. You can run the Python interpreter using a simple graphical interface called the Interactive DeveLopment Environment (IDLE). On a Mac you can find this under Applications -> MacPython, and on Windows under All Programs -> Python. Under Unix you can run Python from the shell by typing python. The interpreter will print a blurb about your Python version; simply check that you are running Python 2.4 or greater (here it is 2.5):
|
Note
If you are unable to run the Python interpreter, you probably don't have Python installed correctly. Please visit http://nltk.org/ for detailed instructions.
The >>> prompt indicates that the Python interpreter is now waiting for input. Let's begin by using the Python prompt as a calculator:
|
Once the interpreter has finished calculating the answer and displaying it, the prompt reappears. This means the Python interpreter is waiting for another instruction.
Try a few more expressions of your own. You can use asterisk (*) for multiplication and slash (/) for division, and parentheses for bracketing expressions. One strange thing you might come across is that division doesn't always behave how you expect:
|
The second case is surprising because we would expect the answer to be 0.333333. We will come back to why that is the case later on in this chapter. For now, let's simply observe that these examples demonstrate how you can work interactively with the interpreter, allowing you to experiment and explore. Also, as you will see later, your intuitions about numerical expressions will be useful for manipulating other kinds of data in Python.
You should also try nonsensical expressions to see how the interpreter handles it:
|
Here we have produced a syntax error. It doesn't make sense to end an instruction with a plus sign. The Python interpreter indicates the line where the problem occurred.
1.2.2 Searching Text
Now that we can use the Python interpreter, let's see how we can harness its power to process text. The first step is to type a line of magic at the Python prompt, telling the interpreter to load some texts for us to explore: from nltk.text import *. After printing a welcome message, it loads the text of several books, including Moby Dick. We can ask the interpreter to give us some information about it, such as title and word length, by typing text1, and len(text1):
|
We can examine the contents of the book in a variety of ways. A concordance view shows us a given word in its context. Here we look up the word monstrous. Try seaching for other words; you can use the up-arrow key to access the previous command and modify the word being searched.
|
You can now try concordance searches on some of the other texts we have included. For example, to search Sense and Sensibility by Jane Austen, for the word affection, use: text2.concordance('affection'). Search the book of Genesis to find out how long some people lived, using: text3.concordance('lived'). You could look at text4, the US Presidential Inaugural Addresses to see examples of English dating back to 1789, and search for words like nation, terror, god. We've also included text5, the NPS Chat Corpus: search this for unconventional words like im, ur, lol.
Once you've spent some time examining these texts, we hope you have a new sense of the richness and diversity of language. In the next chapter you will learn how to access a broader range of text, including text in languages other than English.
If we can find words in a text, we can also take note of their position within the text. We produce a dispersion plot, where each bar represents an instance of a word and each row represents the entire text. In Figure 1.1 we see characteristically different roles played by the male and female protagonists in Sense and Sensibility. In Figure 1.2 we see some striking patterns of word usage over the last 220 years. You can produce these plots as shown below. You might like to try different words, and different texts.
|
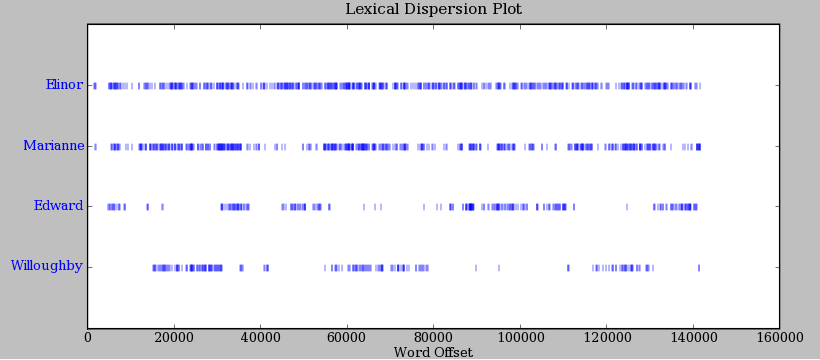
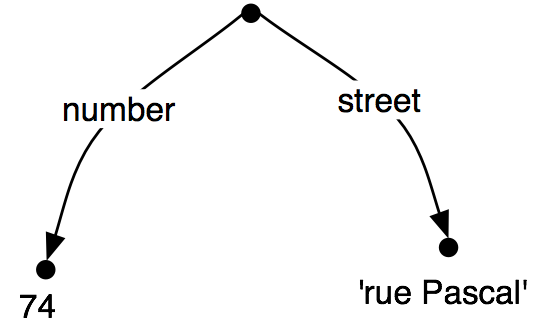
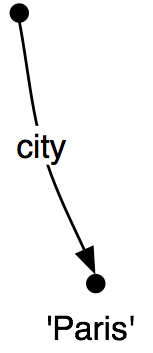
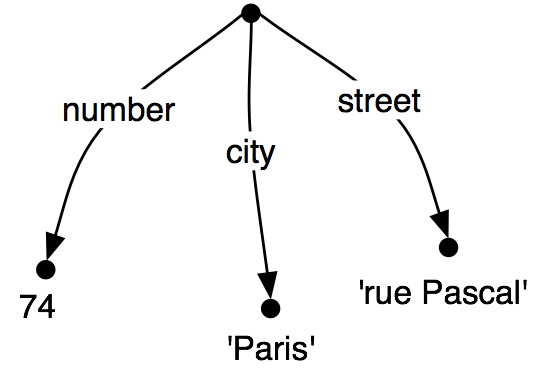
Figure 1.1: Lexical Dispersion Plot for Main Protagonists in Sense and Sensibility
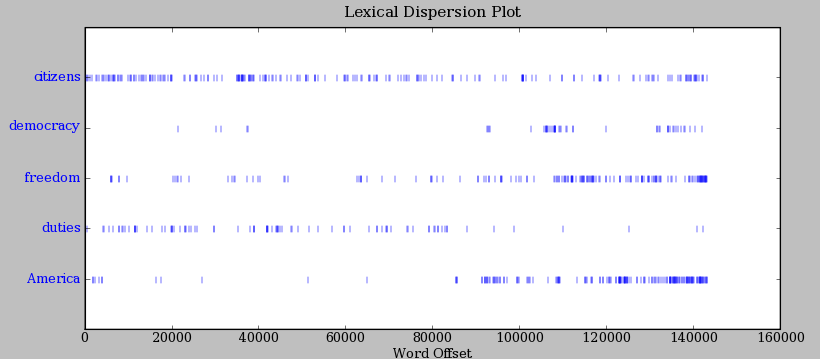
Figure 1.2: Lexical Dispersion Plot for Words in Presidential Inaugural Addresses
A concordance permits us to see words in context, e.g. we saw that monstrous appeared in the context the monstrous pictures. What other words appear in the same contexts that monstrous appears in? We can find out as follows:
|
Observe that we get different results for different books.
Now, just for fun, let's try generating some random text in the various styles we have just seen. To do this, we type the name of the text followed by the "generate" function, e.g. text3.generate():
|
Note that first time you run this, it is slow because it gathers statistics about word sequences. Each time you run it, you will get different output text. Now try generating random text in the style of an inaugural address or an internet chat room.
Note
When text is printed, punctuation has been split off from the previous word. Although this is not correct formatting for English text, we do this to make it clear that punctuation does not belong to the word. This is called "tokenization", and we will learn more about it in Chapter 2.
1.2.3 Counting Vocabulary
The most obvious fact about texts that emerges from the previous section is that they differ in the vocabulary they use. In this section we will see how to use the computer to count the words in a text, in a variety of useful ways. As before you will jump right in and experiment with the Python interpreter, even though you may not have studied Python systematically yet.
Let's begin by finding out the length of a text from start to finish, in terms of the words and punctuation symbols that appear. Let's look at the text of Moby Dick:
|
That's a quarter of a million words long! How many distinct words does this text contain? To work this out in Python we have to pose the question slightly differently. The vocabulary of a text is just the set of words that it uses, and in Python we can list the vocabulary of text3 with the command: set(text3). This will produce many screens of words. Now try the following:
|
Thus we can see a sorted list of vocabulary items beginning with various punctuation symbols. We can find out the size of the vocabulary by asking for the length of the set. Finally, we can calculate a measure of the lexical richness of the text and learn that each word is used 16 times on average.
We might like to repeat the last of these calculations on several texts, but it is tedious to keep retyping this line for different texts. Instead, we can come up with our own name for this task, e.g. "score", and define a function that can be re-used as often as we like:
|
Note
The Python interpreter changes the prompt from >>> to ... after encountering the colon at the end of the first line. The ... prompt indicates that Python expects an indented code block to appear next. It is up to you to do the indentation, by typing four spaces. To finish the indented block just enter a blank line.
Notice that we used the score function by typing its name, followed by an open parenthesis, the name of the text, then a close parenthesis. This is just what we did for the len and set functions earlier. These parentheses will show up often: their role is to separate the name of a task — such as score — from the data that the task is to be performed on — such as text3.
Now that we've had an initial sample of language processing in Python, we will continue with a systematic introduction to the language.
1.3 Python Basics: Strings and Variables
1.3.1 Representing text
We can't simply type text directly into the interpreter because it would try to interpret the text as part of the Python language:
|
Here we see an error message. Note that the interpreter is confused about the position of the error, and points to the end of the string rather than the start.
Python represents a piece of text using a string. Strings are delimited — or separated from the rest of the program — by quotation marks:
|
We can use either single or double quotation marks, as long as we use the same ones on either end of the string.
Now we can perform calculator-like operations on strings. For example, adding two strings together seems intuitive enough that you could guess the result:
|
When applied to strings, the + operation is called concatenation. It produces a new string that is a copy of the two original strings pasted together end-to-end. Notice that concatenation doesn't do anything clever like insert a space between the words. The Python interpreter has no way of knowing that you want a space; it does exactly what it is told. Given the example of +, you might be able guess what multiplication will do:
|
The point to take from this (apart from learning about strings) is that in Python, intuition about what should work gets you a long way, so it is worth just trying things to see what happens. You are very unlikely to break anything, so just give it a go.
1.3.2 Storing and Reusing Values
After a while, it can get quite tiresome to keep retyping Python statements over and over again. It would be nice to be able to store the value of an expression like 'Hi' + 'Hi' + 'Hi' so that we can use it again. We do this by saving results to a location in the computer's memory, and giving the location a name. Such a named place is called a variable. In Python we create variables by assignment, which involves putting a value into the variable:
In line ![[1]](callouts/callout1.gif) we have created a variable called msg (short for 'message')
and set it to have the string value 'Hello World'. We used the
= operation, which assigns the value of the expression on
the right to the variable on the left. Notice the Python interpreter
does not print any output; it only prints output when the statement
returns a value, and an assignment statement returns no value. In line
we have created a variable called msg (short for 'message')
and set it to have the string value 'Hello World'. We used the
= operation, which assigns the value of the expression on
the right to the variable on the left. Notice the Python interpreter
does not print any output; it only prints output when the statement
returns a value, and an assignment statement returns no value. In line
![[2]](callouts/callout2.gif) we inspect the contents of the variable by naming it on
the command line: that is, we use the name msg. The interpreter
prints out the contents of the variable in line
we inspect the contents of the variable by naming it on
the command line: that is, we use the name msg. The interpreter
prints out the contents of the variable in line ![[3]](callouts/callout3.gif) .
.
Variables stand in for values, so instead of writing 'Hi' * 3 we could assign variable msg the value 'Hi', and num the value 3, then perform the multiplication using the variable names:
|
The names we choose for the variables are up to us. Instead of msg and num, we could have used any names we like:
|
Thus, the reason for choosing meaningful variable names is to help you — and anyone who reads your code — to understand what it is meant to do. Python does not try to make sense of the names; it blindly follows your instructions, and does not object if you do something potentially confusing such as assigning a variable two the value 3, with the assignment statement: two = 3.
Note that we can also assign a new value to a variable just by using assignment again:
|
Here we have taken the value of msg, multiplied it by 3 and then stored that new string (HiHiHi) back into the variable msg.
1.3.3 Printing and Inspecting Strings
So far, when we have wanted to look at the contents of a variable or see the result of a calculation, we have just typed the variable name into the interpreter. We can also see the contents of msg using print msg:
|
On close inspection, you will see that the quotation marks that indicate that Hello World is a string are missing in the second case. That is because inspecting a variable, by typing its name into the interactive interpreter, prints out the Python representation of a value. In contrast, the print statement only prints out the value itself, which in this case is just the text contained in the string.
In fact, you can use a sequence of comma-separated expressions in a print statement:
|
Note
If you have created some variable v and want to find out about it, then type help(v) to read the help entry for this kind of object. Type dir(v) to see a list of operations that are defined on the object.
You need to be a little bit careful in your choice of names (or identifiers) for Python variables. Some of the things you might try will cause an error. First, you should start the name with a letter, optionally followed by digits (0 to 9) or letters. Thus, abc23 is fine, but 23abc will cause a syntax error. You can use underscores (both within and at the start of the variable name), but not a hyphen, since this gets interpreted as an arithmetic operator. A second problem is shown in the following snippet.
|
Why is there an error here? Because not is reserved as one of Python's 30 odd keywords. These are special identifiers that are used in specific syntactic contexts, and cannot be used as variables. It is easy to tell which words are keywords if you use IDLE, since they are helpfully highlighted in orange.
1.3.4 Creating Programs with a Text Editor
The Python interative interpreter performs your instructions as soon as you type them. Often, it is better to compose a multi-line program using a text editor, then ask Python to run the whole program at once. Using IDLE, you can do this by going to the File menu and opening a new window. Try this now, and enter the following one-line program:
msg = 'Hello World'
Save this program in a file called test.py, then go to the Run menu, and select the command Run Module. The result in the main IDLE window should look like this:
|
Now, where is the output showing the value of msg? The answer is that the program in test.py will show a value only if you explicitly tell it to, using the print command. So add another line to test.py so that it looks as follows:
msg = 'Hello World' print msg
Select Run Module again, and this time you should get output that looks like this:
|
From now on, you have a choice of using the interactive interpreter or a text editor to create your programs. It is often convenient to test your ideas using the interpreter, revising a line of code until it does what you expect, and consulting the interactive help facility. Once you're ready, you can paste the code (minus any >>> prompts) into the text editor, continue to expand it, and finally save the program in a file so that you don't have to retype it in again later.
1.3.5 Exercises
☼ Start up the Python interpreter (e.g. by running IDLE). Try the examples in section 1.2, then experiment with using Python as a calculator.
☼ Try the examples in this section, then try the following.
Create a variable called msg and put a message of your own in this variable. Remember that strings need to be quoted, so you will need to type something like:
>>> msg = "I like NLP!"
Now print the contents of this variable in two ways, first by simply typing the variable name and pressing enter, then by using the print command.
Try various arithmetic expressions using this string, e.g. msg + msg, and 5 * msg.
Define a new string hello, and then try hello + msg. Change the hello string so that it ends with a space character, and then try hello + msg again.
☺ Discuss the steps you would go through to find the ten most frequent words in a two-page document.
1.4 Slicing and Dicing
Strings are so important that we will spend some more time on them. Here we will learn how to access the individual characters that make up a string, how to pull out arbitrary substrings, and how to reverse strings.
1.4.1 Accessing Individual Characters
The positions within a string are numbered, starting from zero. To access a position within a string, we specify the position inside square brackets:
|
This is called indexing or subscripting the string. The position we specify inside the square brackets is called the index. We can retrieve not only letters but any character, such as the space at index 5.
Note
Be careful to distinguish between the string ' ', which is a single whitespace character, and '', which is the empty string.
The fact that strings are indexed from zero may seem counter-intuitive. You might just want to think of indexes as giving you the position in a string immediately before a character, as indicated in Figure 1.3.

Figure 1.3: String Indexing
Now, what happens when we try to access an index that is outside of the string?
|
The index of 11 is outside of the range of valid indices (i.e., 0 to 10) for the string 'Hello World'. This results in an error message. This time it is not a syntax error; the program fragment is syntactically correct. Instead, the error occurred while the program was running. The Traceback message indicates which line the error occurred on (line 1 of "standard input"). It is followed by the name of the error, IndexError, and a brief explanation.
In general, how do we know what we can index up to? If we know the length of the string is n, the highest valid index will be n-1. We can get access to the length of the string using the built-in len() function.
|
Informally, a function is a named snippet of code that provides a service to our program when we call or execute it by name. We call the len() function by putting parentheses after the name and giving it the string msg we want to know the length of. Because len() is built into the Python interpreter, IDLE colors it purple.
We have seen what happens when the index is too large. What about when it is too small? Let's see what happens when we use values less than zero:
|
This does not generate an error. Instead, negative indices work from the end of the string, so -1 indexes the last character, which is 'd'.
|
Now the computer works out the location in memory relative to the string's address plus its length, subtracting the index, e.g. 3136 + 11 - 1 = 3146. We can also visualize negative indices as shown in Figure 1.4.
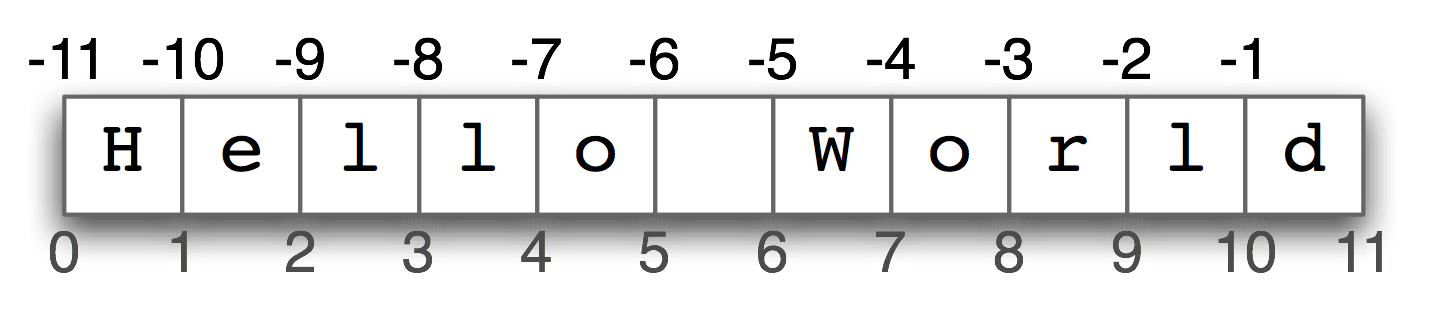
Figure 1.4: Negative Indices
Thus we have two ways to access the characters in a string, from the start or the end. For example, we can access the space in the middle of Hello and World with either msg[5] or msg[-6]; these refer to the same location, because 5 = len(msg) - 6.
1.4.2 Accessing Substrings
In NLP we usually want to access more than one character at a time. This is also pretty simple; we just need to specify a start and end index. For example, the following code accesses the substring starting at index 1, up to (but not including) index 4:
|
The notation :4 is known as a slice. Here we see the characters are 'e', 'l' and 'l' which correspond to msg[1], msg[2] and msg[3], but not msg[4]. This is because a slice starts at the first index but finishes one before the end index. This is consistent with indexing: indexing also starts from zero and goes up to one before the length of the string. We can see this by slicing with the value of len():
|
We can also slice with negative indices — the same basic rule of starting from the start index and stopping one before the end index applies; here we stop before the space character:
|
Python provides two shortcuts for commonly used slice values. If the start index is 0 then you can leave it out, and if the end index is the length of the string then you can leave it out:
|
The first example above selects the first three characters from the string, and the second example selects from the character with index 6, namely 'W', to the end of the string.
1.4.3 Exercises
☼ Define a string s = 'colorless'. Write a Python statement that changes this to "colourless" using only the slice and concatenation operations.
☼ Try the slice examples from this section using the interactive interpreter. Then try some more of your own. Guess what the result will be before executing the command.
☼ We can use the slice notation to remove morphological endings on words. For example, 'dogs'[:-1] removes the last character of dogs, leaving dog. Use slice notation to remove the affixes from these words (we've inserted a hyphen to indicate the affix boundary, but omit this from your strings): dish-es, run-ning, nation-ality, un-do, pre-heat.
☼ We saw how we can generate an IndexError by indexing beyond the end of a string. Is it possible to construct an index that goes too far to the left, before the start of the string?
☼ We can also specify a "step" size for the slice. The following returns every second character within the slice, in a forward or reverse direction:
>>> msg[6:11:2] 'Wrd' >>> msg[10:5:-2] 'drW' >>>
Experiment with different step values.
☼ What happens if you ask the interpreter to evaluate msg[::-1]? Explain why this is a reasonable result.
1.5 Strings, Sequences, and Sentences
We have seen how words like Hello can be stored as a string 'Hello'. Whole sentences can also be stored in strings, and manipulated as before, as we can see here for Chomsky's famous nonsense sentence:
|
However, it turns out to be a bad idea to treat a sentence as a sequence of its characters, because this makes it too inconvenient to access the words. Instead, we would prefer to represent a sentence as a sequence of its words; as a result, indexing a sentence accesses the words, rather than characters. We will see how to do this now.
1.5.1 Lists
A list is designed to store a sequence of values. A list is similar to a string in many ways except that individual items don't have to be just characters; they can be arbitrary strings, integers or even other lists.
A Python list is represented as a sequence of comma-separated items, delimited by square brackets. Here are some lists:
|
We can also store sentences and phrases using lists. Let's create part of Chomsky's sentence as a list and put it in a variable cgi:
|
Because lists and strings are both kinds of sequence, they can be processed in similar ways; just as strings support len(), indexing and slicing, so do lists. The following example applies these familiar operations to the list cgi:
|
Here, cgi[-5] generates an error, because the fifth-last item in a three item list would occur before the list started, i.e., it is undefined. We can also slice lists in exactly the same way as strings:
|
Lists can be concatenated just like strings. Here we will put the resulting list into a new variable chomsky. The original variable cgi is not changed in the process:
|
Now, lists and strings do not have exactly the same functionality. Lists have the added power that you can change their elements. Let's imagine that we want to change the 0th element of cgi to 'colorful', we can do that by assigning the new value to the index cgi[0]:
|
On the other hand if we try to do that with a string — changing the 0th character in msg to 'J' — we get:
|
This is because strings are immutable — you can't change a string once you have created it. However, lists are mutable, and their contents can be modified at any time. As a result, lists support a number of operations, or methods, that modify the original value rather than returning a new value. A method is a function that is associated with a particular object. A method is called on the object by giving the object's name, then a period, then the name of the method, and finally the parentheses containing any arguments. For example, in the following code we use the sort() and reverse() methods:
|
As you will see, the prompt reappears immediately on the line after chomsky.sort() and chomsky.reverse(). That is because these methods do not produce a new list, but instead modify the original list stored in the variable chomsky.
Lists also have an append() method for adding items to the end of the list and an index() method for finding the index of particular items in the list:
|
Finally, just as a reminder, you can create lists of any values you like. As you can see in the following example for a lexical entry, the values in a list do not even have to have the same type (though this is usually not a good idea, as we will explain in Section 5.2).
|
1.5.2 Working on Sequences One Item at a Time
We have shown you how to create lists, and how to index and manipulate them in various ways. Often it is useful to step through a list and process each item in some way. We do this using a for loop. This is our first example of a control structure in Python, a statement that controls how other statements are run:
|
The for loop has the general form: for variable in sequence followed by a colon, then an indented block of code. The first time through the loop, the variable is assigned to the first item in the sequence, i.e. num has the value 1. This program runs the statement print 'The number is', num for this value of num, before returning to the top of the loop and assigning the second item to the variable. Once all items in the sequence have been processed, the loop finishes.
Now let's try the same idea with a list of words:
|
The first time through this loop, the variable is assigned the value 'colorless'. This program runs the statement print len(word), word[-1], word for this value, to produce the output line: 9 s colorless. This process is known as iteration. Each iteration of the for loop starts by assigning the next item of the list chomsky to the loop variable word. Then the indented body of the loop is run. Here the body consists of a single command, but in general the body can contain as many lines of code as you want, so long as they are all indented by the same amount. (We recommend that you always use exactly 4 spaces for indentation, and that you never use tabs.)
We can run another for loop over the Chomsky nonsense sentence, and calculate the average word length. As you will see, this program uses the len() function in two ways: to count the number of characters in a word, and to count the number of words in a phrase. Note that x += y is shorthand for x = x + y; this idiom allows us to increment the total variable each time the loop is run.
|
We can also write for loops to iterate over the characters in strings. This print statement ends with a trailing comma, which is how we tell Python not to print a newline at the end.
|
A note of caution: we have now iterated over words and characters, using expressions like for word in sent: and for char in sent:. Remember that, to Python, word and char are meaningless variable names, and we could just as well have written for foo123 in sent:. The interpreter simply iterates over the items in the sequence, quite oblivious to what kind of object they represent, e.g.:
|
However, you should try to choose 'sensible' names for loop variables because it will make your code more readable.
1.5.3 String Formatting
The output of a program is usually structured to make the information easily digestible by a reader. Instead of running some code and then manually inspecting the contents of a variable, we would like the code to tabulate some output. We already saw this above in the first for loop example that used a list of words, where each line of output was similar to 5 p sleep, consisting of a word length, the last character of the word, then the word itself.
There are many ways we might want to format such output. For instance, we might want to place the length value in parentheses after the word, and print all the output on a single line:
|
However, this approach has a couple of problems. First, the print statement intermingles variables and punctuation, making it a little difficult to read. Second, the output has spaces around every item that was printed. A cleaner way to produce structured output uses Python's string formatting expressions. Before diving into clever formatting tricks, however, let's look at a really simple example. We are going to use a special symbol, %s, as a placeholder in strings. Once we have a string containing this placeholder, we follow it with a single % and then a value v. Python then returns a new string where v has been slotted in to replace %s:
|
In fact, we can have a number of placeholders, but following the % operator we need to specify exactly the same number of values. Note that the parentheses are required.
|
We can also provide the values for the placeholders indirectly. Here's an example using a for loop:
|
We oversimplified things when we said that placeholders were of the form %s; in fact, this is a complex object, called a conversion specifier. This has to start with the % character, and ends with conversion character such as s` or ``d. The %s specifier tells Python that the corresponding variable is a string (or should be converted into a string), while the %d specifier indicates that the corresponding variable should be converted into a decimal representation. The string containing conversion specifiers is called a format string.
Picking up on the print example that we opened this section with, here's how we can use two different kinds of conversion specifier:
|
To summarize, string formatting is accomplished with a three-part object having the syntax: format % values. The format section is a string containing format specifiers such as %s and %d that Python will replace with the supplied values. The values section of a formatting string is a parenthesized list containing exactly as many items as there are format specifiers in the format section. In the case that there is just one item, the parentheses can be left out. (We will discuss Python's string-formatting expressions in more detail in Section 5.3.2).
In the above example, we used a trailing comma to suppress the printing of a newline. Suppose, on the other hand, that we want to introduce some additional newlines in our output. We can accomplish this by inserting the "special" character \n into the print string:
|
1.5.4 Converting Between Strings and Lists
Often we want to convert between a string containing a space-separated list of words and a list of strings. Let's first consider turning a list into a string. One way of doing this is as follows:
|
One drawback of this approach is that we have an unwanted space at the start of s. It is more convenient to use the join() method. We specify the string to be used as the "glue", followed by a period, followed by the join() function.
|
So ' '.join(chomsky) means: take all the items in chomsky and concatenate them as one big string, using ' ' as a spacer between the items.
Now let's try to reverse the process: that is, we want to convert a string into a list. Again, we could start off with an empty list [] and append() to it within a for loop. But as before, there is a more succinct way of achieving the same goal. This time, we will split the new string sent on whitespace:
To consolidate your understanding of joining and splitting strings, let's try the same thing using a semicolon as the separator:
|
To be honest, many people find the notation for join() rather unintuitive. There is another function for converting lists to strings, again called join() which is called directly on the list. It uses whitespace by default as the "glue". However, we need to explicitly import this function into our code. One way of doing this is as follows:
|
Here, we imported something called string, and then called the function string.join(). In passing, if we want to use something other than whitespace as "glue", we just specify this as a second parameter:
|
We will see other examples of statements with import later in this chapter. In general, we use import statements when we want to get access to Python code that doesn't already come as part of core Python. This code will exist somewhere as one or more files. Each such file corresponds to a Python module — this is a way of grouping together code and data that we regard as reusable. When you write down some Python statements in a file, you are in effect creating a new Python module. And you can make your code depend on another module by using the import statement. In our example earlier, we imported the module string and then used the join() function from that module. By adding string. to the beginning of join(), we make it clear to the Python interpreter that the definition of join() is given in the string module. An alternative, and equally valid, approach is to use the from module import identifier statement, as shown in the next example:
|
In this case, the name join is added to all the other identifier that we have defined in the body of our programme, and we can use it to call a function like any other.
Note
If you are creating a file to contain some of your Python code, do not name your file nltk.py: it may get imported in place of the "real" NLTK package. (When it imports modules, Python first looks in the current folder / directory.)
1.5.5 Mini-Review
Strings and lists are both kind of sequence. As such, they can both be indexed and sliced:
|
Similarly, strings can be concatenated and so can lists (though not with each other!):
|
What's the difference between strings and lists as far as NLP is concerned? As we will see in Chapter 2, when we open a file for reading into a Python program, what we get initially is a string, corresponding to the contents of the whole file. If we try to use a for loop to process the elements of this string, all we can pick out are the individual characters in the string — we don't get to choose the granularity. By contrast, the elements of a list can be as big or small as we like: for example, they could be paragraphs, sentence, phrases, words, characters. So lists have this huge advantage, that we can be really flexible about the elements they contain, and correspondingly flexible about what the downstream processing will act on. So one of the first things we are likely to do in a piece of NLP code is convert a string into a list (of strings). Conversely, when we want to write our results to a file, or to a terminal, we will usually convert them to a string.
1.5.6 Exercises
☼ Using the Python interactive interpreter, experiment with the examples in this section. Think of a sentence and represent it as a list of strings, e.g. ['Hello', 'world']. Try the various operations for indexing, slicing and sorting the elements of your list. Extract individual items (strings), and perform some of the string operations on them.
☼ Split sent on some other character, such as 's'.
☼ We pointed out that when phrase is a list, phrase.reverse() returns a modified version of phrase rather than a new list. On the other hand, we can use the slice trick mentioned in the exercises for the previous section, [::-1] to create a new reversed list without changing phrase. Show how you can confirm this difference in behavior.
☼ We have seen how to represent a sentence as a list of words, where each word is a sequence of characters. What does phrase1[2][2] do? Why? Experiment with other index values.
☼ Write a for loop to print out the characters of a string, one per line.
☼ What is the difference between calling split on a string with no argument or with ' ' as the argument, e.g. sent.split() versus sent.split(' ')? What happens when the string being split contains tab characters, consecutive space characters, or a sequence of tabs and spaces? (In IDLE you will need to use '\t' to enter a tab character.)
☼ Create a variable words containing a list of words. Experiment with words.sort() and sorted(words). What is the difference?
☼ Earlier, we asked you to use a text editor to create a file called test.py, containing the single line msg = 'Hello World'. If you haven't already done this (or can't find the file), go ahead and do it now. Next, start up a new session with the Python interpreter, and enter the expression msg at the prompt. You will get an error from the interpreter. Now, try the following (note that you have to leave off the .py part of the filename):
>>> from test import msg >>> msg
This time, Python should return with a value. You can also try import test, in which case Python should be able to evaluate the expression test.msg at the prompt.
◑ Process the list chomsky using a for loop, and store the result in a new list lengths. Hint: begin by assigning the empty list to lengths, using lengths = []. Then each time through the loop, use append() to add another length value to the list.
◑ Define a variable silly to contain the string: 'newly formed bland ideas are inexpressible in an infuriating way'. (This happens to be the legitimate interpretation that bilingual English-Spanish speakers can assign to Chomsky's famous phrase, according to Wikipedia). Now write code to perform the following tasks:
- Split silly into a list of strings, one per word, using Python's split() operation, and save this to a variable called bland.
- Extract the second letter of each word in silly and join them into a string, to get 'eoldrnnnna'.
- Combine the words in bland back into a single string, using join(). Make sure the words in the resulting string are separated with whitespace.
- Print the words of silly in alphabetical order, one per line.
◑ The index() function can be used to look up items in sequences. For example, 'inexpressible'.index('e') tells us the index of the first position of the letter e.
- What happens when you look up a substring, e.g. 'inexpressible'.index('re')?
- Define a variable words containing a list of words. Now use words.index() to look up the position of an individual word.
- Define a variable silly as in the exercise above. Use the index() function in combination with list slicing to build a list phrase consisting of all the words up to (but not including) in in silly.
1.6 Making Decisions
So far, our simple programs have been able to manipulate sequences of words, and perform some operation on each one. We applied this to lists consisting of a few words, but the approach works the same for lists of arbitrary size, containing thousands of items. Thus, such programs have some interesting qualities: (i) the ability to work with language, and (ii) the potential to save human effort through automation. Another useful feature of programs is their ability to make decisions on our behalf; this is our focus in this section.
1.6.1 Making Simple Decisions
Most programming languages permit us to execute a block of code when a conditional expression, or if statement, is satisfied. In the following program, we have created a variable called word containing the string value 'cat'. The if statement then checks whether the condition len(word) < 5 is true. Because the conditional expression is true, the body of the if statement is invoked and the print statement is executed.
|
If we change the conditional expression to len(word) >= 5, to check that the length of word is greater than or equal to 5, then the conditional expression will no longer be true, and the body of the if statement will not be run:
|
The if statement, just like the for statement above is a control structure. An if statement is a control structure because it controls whether the code in the body will be run. You will notice that both if and for have a colon at the end of the line, before the indentation begins. That's because all Python control structures end with a colon.
What if we want to do something when the conditional expression is not true? The answer is to add an else clause to the if statement:
|
Finally, if we want to test multiple conditions in one go, we can use an elif clause that acts like an else and an if combined:
|
It's worth noting that in the condition part of an if statement, a nonempty string or list is evaluated as true, while an empty string or list evaluates as false.
|
That is, we don't need to say if len(element) > 0: in the condition.
What's the difference between using if...elif as opposed to using a couple of if statements in a row? Well, consider the following situation:
|
Since the if clause of the statement is satisfied, Python never tries to evaluate the elif clause, so we never get to print out 2. By contrast, if we replaced the elif by an if, then we would print out both 1 and 2. So an elif clause potentially gives us more information than a bare if clause; when it evaluates to true, it tells us not only that the condition is satisfied, but also that the condition of the main if clause was not satisfied.
1.6.2 Conditional Expressions
Python supports a wide range of operators like < and >= for testing the relationship between values. The full set of these relational operators are shown in Table 1.1.
Operator Relationship < less than <= less than or equal to == equal to (note this is two not one = sign) != not equal to > greater than >= greater than or equal to Table 1.1
Conditional Expressions
Normally we use conditional expressions as part of an if statement. However, we can test these relational operators directly at the prompt:
|
Here we see that these expressions have Boolean values, namely True or False. not is a Boolean operator, and flips the truth value of Boolean statement.
Strings and lists also support conditional operators:
|
Strings also have methods for testing what appears at the beginning and the end of a string (as opposed to just anywhere in the string:
|
1.6.3 Iteration, Items, and if
Now it is time to put some of the pieces together. We are going to take the string 'how now brown cow' and print out all of the words ending in 'ow'. Let's build the program up in stages. The first step is to split the string into a list of words:
|
Next, we need to iterate over the words in the list. Just so we don't get ahead of ourselves, let's print each word, one per line:
|
The next stage is to only print out the words if they end in the string 'ow'. Let's check that we know how to do this first:
|
Now we are ready to put an if statement inside the for loop. Here is the complete program:
|
As you can see, even with this small amount of Python knowledge it is possible to develop useful programs. The key idea is to develop the program in pieces, testing that each one does what you expect, and then combining them to produce whole programs. This is why the Python interactive interpreter is so invaluable, and why you should get comfortable using it.
1.6.4 A Taster of Data Types
Integers, strings and lists are all kinds of data types in Python, and have types int, str and list respectively. In fact, every value in Python has a type. Python's type() function will tell you what an object's type is:
|
The type determines what operations you can perform on the data value. So, for example, we have seen that we can index strings and lists, but we can't index integers:
|
The fact that this is a problem with types is signalled by the class of error, i.e., TypeError; an object being "unsubscriptable" means we can't index into it.
Similarly, we can concatenate strings with strings, and lists with lists, but we cannot concatenate strings with lists:
|
You may also have noticed that our analogy between operations on strings and numbers at the beginning of this chapter broke down pretty soon:
|
These error messages are another example of Python telling us that we have got our data types in a muddle. In the first case, we are told that the operation of substraction (i.e., -) cannot apply to objects of type str, while in the second, we are told that division cannot take str and int as its two operands.
1.6.5 Exercises
☼ Assign a new value to sentence, namely the string 'she sells sea shells by the sea shore', then write code to perform the following tasks:
- Print all words beginning with 'sh':
- Print all words longer than 4 characters.
- Generate a new sentence that adds the popular hedge word 'like' before every word beginning with 'se'. Your result should be a single string.
☼ Write code to abbreviate text by removing all the vowels. Define sentence to hold any string you like, then initialize a new string result to hold the empty string ''. Now write a for loop to process the string, one character at a time, and append any non-vowel characters to the result string.
☼ We pointed out that when empty strings and empty lists occur in the condition part of an if clause, they evaluate to false. In this case, they are said to be occuring in a Boolean context. Experiment with different kind of non-Boolean expressions in Boolean contexts, and see whether they evaluate as true or false.
☼ Review conditional expressions, such as 'row' in 'brown' and 'row' in ['brown', 'cow'].
- Define sent to be the string 'colorless green ideas sleep furiously', and use conditional expressions to test for the presence of particular words or substrings.
- Now define words to be a list of words contained in the sentence, using sent.split(), and use conditional expressions to test for the presence of particular words or substrings.
◑ Write code to convert text into hAck3r, where characters are mapped according to the following table:
Input:
e
i
o
l
s
.
ate
Output:
3
1
0
|
5
5w33t!
8
Table 1.2
1.7 Getting Organized
Strings and lists are a simple way to organize data. In particular, they map from integers to values. We can "look up" a character in a string using an integer, and we can look up a word in a list of words using an integer. These cases are shown in Figure 1.5.

Figure 1.5: Sequence Look-up
However, we need a more flexible way to organize and access our data. Consider the examples in Figure 1.6.

Figure 1.6: Dictionary Look-up
In the case of a phone book, we look up an entry using a name, and get back a number. When we type a domain name in a web browser, the computer looks this up to get back an IP address. A word frequency table allows us to look up a word and find its frequency in a text collection. In all these cases, we are mapping from names to numbers, rather than the other way round as with indexing into sequences. In general, we would like to be able to map between arbitrary types of information. Table 1.3 lists a variety of linguistic objects, along with what they map.
Linguistic Object Maps from to Document Index Word List of pages (where word is found) Thesaurus Word sense List of synonyms Dictionary Headword Entry (part of speech, sense definitions, etymology) Comparative Wordlist Gloss term Cognates (list of words, one per language) Morph Analyzer Surface form Morphological analysis (list of component morphemes) Table 1.3
Linguistic Objects as Mappings from Keys to Values
Most often, we are mapping from a string to some structured object. For example, a document index maps from a word (which we can represent as a string), to a list of pages (represented as a list of integers). In this section, we will see how to represent such mappings in Python.
1.7.1 Accessing Data with Data
Python provides a dictionary data type that can be used for mapping between arbitrary types.
Note
A Python dictionary is somewhat like a linguistic dictionary — they both give you a systematic means of looking things up, and so there is some potential for confusion. However, we hope that it will usually be clear from the context which kind of dictionary we are talking about.
Here we define pos to be an empty dictionary and then add three entries to it, specifying the part-of-speech of some words. We add entries to a dictionary using the familiar square bracket notation:
|
So, for example, pos['colorless'] = 'adj' says that the look-up value of 'colorless' in pos is the string 'adj'.
To look up a value in pos, we again use indexing notation, except now the thing inside the square brackets is the item whose value we want to recover:
|
The item used for look-up is called the key, and the data that is returned is known as the value. As with indexing a list or string, we get an exception when we try to access the value of a key that does not exist:
|
This raises an important question. Unlike lists and strings, where we can use len() to work out which integers will be legal indices, how do we work out the legal keys for a dictionary? Fortunately, we can check whether a key exists in a dictionary using the in operator:
|
Notice that we can use not in to check if a key is missing. Be careful with the in operator for dictionaries: it only applies to the keys and not their values. If we check for a value, e.g. 'adj' in pos, the result is False, since 'adj' is not a key. We can loop over all the entries in a dictionary using a for loop.
|
We can see what the contents of the dictionary look like by inspecting the variable pos. Note the presence of the colon character to separate each key from its corresponding value:
|
Here, the contents of the dictionary are shown as key-value pairs. As you can see, the order of the key-value pairs is different from the order in which they were originally entered. This is because dictionaries are not sequences but mappings. The keys in a mapping are not inherently ordered, and any ordering that we might want to impose on the keys exists independently of the mapping. As we shall see later, this gives us a lot of flexibility.
We can use the same key-value pair format to create a dictionary:
|
Using the dictionary methods keys(), values() and items(), we can access the keys and values as separate lists, and also the key-value pairs:
|
Note that keys are forced to be unique. Suppose we try to use a dictionary to store the fact that the word content is both a noun and a verb:
|
Initially, pos['content'] is given the value 'n', and this is immediately overwritten with the new value 'v'. In other words, there is only one entry for 'content'. If we wanted to store multiple values in that entry, we could use a list, e.g. pos['content'] = ['n', 'v'].
1.7.2 Counting with Dictionaries
The values stored in a dictionary can be any kind of object, not just a string — the values can even be dictionaries. The most common kind is actually an integer. It turns out that we can use a dictionary to store counters for many kinds of data. For instance, we can have a counter for all the letters of the alphabet; each time we get a certain letter we increment its corresponding counter:
|
Observe that in is used here in two different ways: for letter in phrase iterates over every letter, running the body of the for loop. Inside this loop, the conditional expression if letter not in count checks whether the letter is missing from the dictionary. If it is missing, we create a new entry and set its value to zero: count[letter] = 0. Now we are sure that the entry exists, and it may have a zero or non-zero value. We finish the body of the for loop by incrementing this particular counter using the += assignment operator. Finally, we print the dictionary, to see the letters and their counts. This method of maintaining many counters will find many uses, and you will become very familiar with it. To make counting much easier, we can use defaultdict, a special kind of container introduced in Python 2.5. This is also included in NLTK for the benefit of readers who are using Python 2.4, and can be imported as shown below.
|
Note
Calling defaultdict(int) creates a special kind of dictionary. When that dictionary is accessed with a non-existent key — i.e. the first time a particular letter is encountered — then int() is called to produce the initial value for this key (i.e. 0). You can test this by running the above code, then typing count['X'] and seeing that it returns a zero value (and not a KeyError as in the case of normal Python dictionaries). The function defaultdict is very handy and will be used in many places later on.
There are other useful ways to display the result, such as sorting alphabetically by the letter:
|
Note
The function sorted() is similar to the sort() method on sequences, but rather than sorting in-place, it produces a new sorted copy of its argument. Moreover, as we will see very soon, sorted() will work on a wider variety of data types, including dictionaries.
1.7.3 Getting Unique Entries
Sometimes, we don't want to count at all, but just want to make a record of the items that we have seen, regardless of repeats. For example, we might want to compile a vocabulary from a document. This is a sorted list of the words that appeared, regardless of frequency. At this stage we have two ways to do this. The first uses lists, while the second uses sets.
|
There is a better way to do this task using Python's set data type. We can convert sentence into a set, using set(sentence):
|
The order of items in a set is not significant, and they will usually appear in a different order to the one they were entered in. The main point here is that converting a list to a set removes any duplicates. We convert it back into a list, sort it, and print. Here is the complete program:
|
Here we have seen that there is sometimes more than one way to solve a problem with a program. In this case, we used three different built-in data types, a list, a dictionary, and a set. The set data type mostly closely modeled our task, so it required the least amount of work.
1.7.4 Scaling Up
We can use dictionaries to count word occurrences. For example, the following code uses NLTK's corpus reader to load Macbeth and count the frequency of each word. Before we can use NLTK we need to tell Python to load it, using the statement import nltk.
|
You will learn more about accessing corpora in Section 2.2.3. For now, you just need to know that gutenberg.words() returns a list of words, in this case from Shakespeare's play Macbeth, and we are iterating over this list using a for loop. We convert each word to lowercase using the string method word.lower(), and use a dictionary to maintain a set of counters, one per word. Now we can inspect the contents of the dictionary to get counts for particular words:
|
1.7.5 Exercises
- ☺ Review the mappings in Table 1.3. Discuss any other examples of mappings you can think of. What type of information do they map from and to?
- ☼ Using the Python interpreter in interactive mode, experiment with the examples in this section. Create a dictionary d, and add some entries. What happens if you try to access a non-existent entry, e.g. d['xyz']?
- ☼ Try deleting an element from a dictionary, using the syntax del d['abc']. Check that the item was deleted.
- ☼ Create a dictionary e, to represent a single lexical entry for some word of your choice. Define keys like headword, part-of-speech, sense, and example, and assign them suitable values.
- ☼ Create two dictionaries, d1 and d2, and add some entries to each. Now issue the command d1.update(d2). What did this do? What might it be useful for?
- ◑ Write a program that takes a sentence expressed as a single string, splits it and counts up the words. Get it to print out each word and the word's frequency, one per line, in alphabetical order.
1.8 Regular Expressions
For a moment, imagine that you are editing a large text, and you have strong dislike of repeated occurrences of the word very. How could you find all such cases in the text? To be concrete, let's suppose that we assign the following text to the variable s:
|
Python's triple quotes """ are used here since they allow us to break a string across lines.
One approach to our task would be to convert the string into a list, and look for adjacent items that are both equal to the string 'very'. We use the range(n) function in this example to create a list of consecutive integers from 0 up to, but not including, n:
|
However, such an approach is not very flexible or convenient. In this section, we will present Python's regular expression module re, which supports powerful search and substitution inside strings. As a gentle introduction, we will start out using a utility function re_show() to illustrate how regular expressions match against substrings. re_show() takes two arguments, a pattern that it is looking for, and a string in which the pattern might occur.
|
(We have only displayed the first part of s that is returned, since the rest is irrelevant for the moment.) As you can see, re_show places curly braces around the first occurrence it has found of the string 'very very'. So an important part of what re_show is doing is searching for any substring of s that matches the pattern in its first argument.
Now we might want to modify the example so that re_show highlights cases where there are two or more adjacent sequences of 'very'. To do this, we need to use a regular expression operator, namely '+'. If s is a string, then s+ means: 'match one or more occurrences of s'. Let's first look at the case where s is a single character, namely the letter 'o':
|
'o+' is our first proper regular expression. You can think of it as matching an infinite set of strings, namely the set {'o', 'oo', 'ooo', ...}. But we would really like to match sequences of least two 'o's; for this, we need the regular expression 'oo+', which matches any string consisting of 'o' followed by one or more occurrences of o.
|
Let's return to the task of identifying multiple occurrences of 'very'. Some initially plausible candidates won't do what we want. For example, 'very+' would match 'veryyy' (but not 'very very'), since the + scopes over the immediately preceding expression, in this case 'y'. To widen the scope of +, we need to use parentheses, as in '(very)+'. Will this match 'very very'? No, because we've forgotten about the whitespace between the two words; instead, it will match strings like 'veryvery'. However, the following does work:
|
Characters preceded by a \, such as '\s', have a special interpretation inside regular expressions; thus, '\s' matches a whitespace character. We could have used ' ' in our pattern, but '\s' is better practice in general. One reason is that the sense of "whitespace" we are using is more general than you might have imagined; it includes not just inter-word spaces, but also tabs and newlines. If you try to inspect the variable s, you might initially get a shock:
|
You might recall that '\n' is a special character that corresponds to a newline in a string. The following example shows how newline is matched by '\s'.
|
Python's re.findall(patt, s) function is a useful way to find all the substrings in s that are matched by patt. Before illustrating, let's introduce two further special characters, '\d' and '\w': the first will match any digit, and the second will match any alphanumeric character. Before we can use re.findall() we have to load Python's regular expression module, using import re.
|
As you will see, the second example matches three-letter words. However, this regular expression is not quite what we want. First, the leading and trailing spaces are extraneous. Second, it will fail to match against strings such as 'the San', where two three-letter words are adjacent. To solve this problem, we can use another special character, namely '\b'. This is sometimes called a "zero-width" character; it matches against the empty string, but only at the beginning and end of words:
|
Note
This example uses a Python raw string: r'\b\w\w\w\b'. The specific justification here is that in an ordinary string, \b is interpreted as a backspace character. Python will convert it to a backspace in a regular expression unless you use the r prefix to create a raw string as shown above. Another use for raw strings is to match strings that include backslashes. Suppose we want to match 'either\or'. In order to create a regular expression, the backslash needs to be escaped, since it is a special character; so we want to pass the pattern \\ to the regular expression interpreter. But to express this as a Python string literal, each backslash must be escaped again, yielding the string '\\\\'. However, with a raw string, this reduces down to r'\\'.
Returning to the case of repeated words, we might want to look for cases involving 'very' or 'really', and for this we use the disjunction operator |.
|
In addition to the matches just illustrated, the regular expression '((very|really)\s)+' will also match cases where the two disjuncts occur with each other, such as the string 'really very really '.
Let's now look at how to perform substitutions, using the re.sub() function. In the first instance we replace all instances of l with s. Note that this generates a string as output, and doesn't modify the original string. Then we replace any instances of green with red.
|
We can also disjoin individual characters using a square bracket notation. For example, [aeiou] matches any of a, e, i, o, or u, that is, any vowel. The expression [^aeiou] matches any single character that is not a vowel. In the following example, we match sequences consisting of a non-vowel followed by a vowel.
|
Using the same regular expression, the function re.findall() returns a list of all the substrings in sent that are matched:
|
1.8.1 Groupings
Returning briefly to our earlier problem with unwanted whitespace around three-letter words, we note that re.findall() behaves slightly differently if we create groups in the regular expression using parentheses; it only returns strings that occur within the groups:
|
The same device allows us to select only the non-vowel characters that appear before a vowel:
|
By delimiting a second group in the regular expression, we can even generate pairs (or tuples) that we may then go on and tabulate.
|
Our next example also makes use of groups. One further special character is the so-called wildcard element, '.'; this has the distinction of matching any single character (except '\n'). Given the string s3, our task is to pick out login names and email domains:
|
The task is made much easier by the fact that all the email addresses in the example are delimited by angle brackets, and we can exploit this feature in our regular expression:
|
Since '.' matches any single character, '.+' will match any non-empty string of characters, including punctuation symbols such as the period.
One question that might occur to you is how do we specify a match against a period? The answer is that we have to place a '\' immediately before the '.' in order to escape its special interpretation.
|
Now, let's suppose that we wanted to match occurrences of both 'Google' and 'google' in our sample text. If you have been following up till now, you would reasonably expect that this regular expression with a disjunction would do the trick: '(G|g)oogle'. But look what happens when we try this with re.findall():
|
What is going wrong? We innocently used the parentheses to indicate the scope of the operator '|', but re.findall() has interpreted them as marking a group. In order to tell re.findall() "don't try to do anything special with these parentheses", we need an extra piece of notation:
|
Placing '?:' immediately after the opening parenthesis makes it explicit that the parentheses are just being used for scoping.
1.8.2 Practice Makes Perfect
Regular expressions are very flexible and very powerful. However, they often don't do what you expect. For this reason, you are strongly encouraged to try out a variety of tasks using re_show() and re.findall() in order to develop your intuitions further; the exercises below should help get you started. We suggest that you build up a regular expression in small pieces, rather than trying to get it completely right first time. Here are some operators and sequences that are commonly used in natural language processing.
Commonly-used Operators and Sequences * Zero or more, e.g. a*, [a-z]* + One or more, e.g. a+, [a-z]+ ? Zero or one (i.e. optional), e.g. a?, [a-z]? [..] A set or range of characters, e.g. [aeiou], [a-z0-9] (..) Grouping parentheses, e.g. (the|a|an) \b Word boundary (zero width) \d Any decimal digit (\D is any non-digit) \s Any whitespace character (\S is any non-whitespace character) \w Any alphanumeric character (\W is any non-alphanumeric character \t The tab character \n The newline character Table 1.4
1.8.3 Exercises
☼ Describe the class of strings matched by the following regular expressions. Note that '*' means: match zero or more occurrences of the preceding regular expression.
- [a-zA-Z]+
- [A-Z][a-z]*
- \d+(\.\d+)?
- ([bcdfghjklmnpqrstvwxyz][aeiou][bcdfghjklmnpqrstvwxyz])*
- \w+|[^\w\s]+
Test your answers using re_show().
☼ Write regular expressions to match the following classes of strings:
- A single determiner (assume that a, an, and the are the only determiners).
- An arithmetic expression using integers, addition, and multiplication, such as 2*3+8.
◑ The above example of extracting (name, domain) pairs from text does not work when there is more than one email address on a line, because the + operator is "greedy" and consumes too much of the input.
- Experiment with input text containing more than one email address per line, such as that shown below. What happens?
- Using re.findall(), write another regular expression to extract email addresses, replacing the period character with a range or negated range, such as [a-z]+ or [^ >]+.
- Now try to match email addresses by changing the regular expression .+ to its "non-greedy" counterpart, .+?
>>> s = """ ... austen-emma.txt:hart@vmd.cso.uiuc.edu (internet) hart@uiucvmd (bitnet) ... austen-emma.txt:Internet (72600.2026@compuserve.com); TEL: (212-254-5093) ... austen-persuasion.txt:Editing by Martin Ward (Martin.Ward@uk.ac.durham) ... blake-songs.txt:Prepared by David Price, email ccx074@coventry.ac.uk ... """
◑ Write code to convert text into Pig Latin. This involves two steps: move any consonant (or consonant cluster) that appears at the start of the word to the end, then append ay, e.g. string → ingstray, idle → idleay. http://en.wikipedia.org/wiki/Pig_Latin
◑ Write code to convert text into hAck3r again, this time using regular expressions and substitution, where e → 3, i → 1, o → 0, l → |, s → 5, . → 5w33t!, ate → 8. Normalize the text to lowercase before converting it. Add more substitutions of your own. Now try to map s to two different values: $ for word-initial s, and 5 for word-internal s.
★ Read the Wikipedia entry on Soundex. Implement this algorithm in Python.
1.9 Summary
- Text is represented in Python using strings, and we type these with single or double quotes: 'Hello', "World".
- The characters of a string are accessed using indexes, counting from zero: 'Hello World'[1] gives the value e. The length of a string is found using len().
- Substrings are accessed using slice notation: 'Hello World'[1:5] gives the value ello. If the start index is omitted, the substring begins at the start of the string; if the end index is omitted, the slice continues to the end of the string.
- Sequences of words are represented in Python using lists of strings: ['colorless', 'green', 'ideas']. We can use indexing, slicing and the len() function on lists.
- Strings can be split into lists: 'Hello World'.split() gives ['Hello', 'World']. Lists can be joined into strings: '/'.join(['Hello', 'World']) gives 'Hello/World'.
- Lists can be sorted in-place: words.sort(). To produce a separate, sorted copy, use: sorted(words).
- We process each item in a string or list using a for statement: for word in phrase. This must be followed by the colon character and an indented block of code, to be executed each time through the loop.
- We test a condition using an if statement: if len(word) < 5. This must be followed by the colon character and an indented block of code, to be executed only if the condition is true.
- A dictionary is used to map between arbitrary types of information, such as a string and a number: freq['cat'] = 12. We create dictionaries using the brace notation: pos = {}, pos = {'furiously': 'adv', 'ideas': 'n', 'colorless': 'adj'}.
- Some functions are not available by default, but must be accessed using Python's import statement.
- Regular expressions are a powerful and flexible method of specifying patterns. Once we have imported the re module, we can use re.findall() to find all substrings in a string that match a pattern, and we can use re.sub() to replace substrings of one sort with another.
1.10 Further Reading
1.10.1 Python
Two freely available online texts are the following:
- Josh Cogliati, Non-Programmer's Tutorial for Python, http://en.wikibooks.org/wiki/Non-Programmer's_Tutorial_for_Python/Contents
- Allen B. Downey, Jeffrey Elkner and Chris Meyers, How to Think Like a Computer Scientist: Learning with Python, http://www.ibiblio.org/obp/thinkCSpy/
An Introduction to Python [Rossum & Jr., 2006] is a Python tutorial by Guido van Rossum, the inventor of Python and Fred L. Drake, Jr., the official editor of the Python documentation. It is available online at http://docs.python.org/tut/tut.html. A more detailed but still introductory text is [Lutz & Ascher, 2003], which covers the essential features of Python, and also provides an overview of the standard libraries.
[Beazley, 2006] is a succinct reference book; although not suitable as an introduction to Python, it is an excellent resource for intermediate and advanced programmers.
Finally, it is always worth checking the official Python Documentation at http://docs.python.org/.
1.10.2 Regular Expressions
There are many references for regular expressions, both practical and theoretical. [Friedl, 2002] is a comprehensive and detailed manual in using regular expressions, covering their syntax in most major programming languages, including Python.
For an introductory tutorial to using regular expressions in Python with the re module, see A. M. Kuchling, Regular Expression HOWTO, http://www.amk.ca/python/howto/regex/.
Chapter 3 of [Mertz, 2003] provides a more extended tutorial on Python's facilities for text processing with regular expressions.
http://www.regular-expressions.info/ is a useful online resource, providing a tutorial and references to tools and other sources of information.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
2 Words: The Building Blocks of Language
2.1 Introduction
Language can be divided up into pieces of varying sizes, ranging from morphemes to paragraphs. In this chapter we will focus on words, the most fundamental level for NLP. Just what are words, and how should we represent them in a machine? These questions may seem trivial, but we'll see that there are some important issues involved in defining and representing words. Once we've tackled them, we're in a good position to do further processing, such as find related words and analyze the style of a text (this chapter), to categorize words (Chapter 3), to group them into phrases (Chapter 6 and Part II), and to do a variety of data-intensive language processing tasks (Chapter 4).
In the following sections, we will explore the division of text into words; the distinction between types and tokens; sources of text data including files, the web, and linguistic corpora; accessing these sources using Python and NLTK; stemming and normalization; the WordNet lexical database; and a variety of useful programming tasks involving words.
Note
From this chapter onwards, our program samples will assume you begin your interactive session or your program with: import nltk, re, pprint
2.2 Tokens, Types and Texts
In Chapter chap-programming, we showed how a string could be split into a list of words. Once we have derived a list, the len() function will count the number of words it contains:
|
This process of segmenting a string of characters into words is known as tokenization. Tokenization is a prelude to pretty much everything else we might want to do in NLP, since it tells our processing software what our basic units are. We will discuss tokenization in more detail shortly.
We also pointed out that we could compile a list of the unique vocabulary items in a string by using set() to eliminate duplicates:
|
So if we ask how many words there are in sentence, we get different answers depending on whether we count duplicates. Clearly we are using different senses of "word" here. To help distinguish between them, let's introduce two terms: token and type. A word token is an individual occurrence of a word in a concrete context; it exists in time and space. A word type is a more abstract; it's what we're talking about when we say that the three occurrences of the in sentence are "the same word."
Something similar to a type-token distinction is reflected in the following snippet of Python:
|
The operator == tests whether two expressions are equal, and in this case, it is testing for string-identity. This is the notion of identity that was assumed by our use of set() above. By contrast, the is operator tests whether two objects are stored in the same location of memory, and is therefore analogous to token-identity. When we used split() to turn a string into a list of words, our tokenization method was to say that any strings that are delimited by whitespace count as a word token. But this simple approach doesn't always give the desired results. Also, testing string-identity isn't a very useful criterion for assigning tokens to types. We therefore need to address two questions in more detail: Tokenization: Which substrings of the original text should be treated as word tokens? Type definition: How do we decide whether two tokens have the same type?
To see the problems with our first stab at defining tokens and types in sentence, let's look at the actual tokens we found:
|
Observe that 'time' and 'time.' are incorrectly treated as distinct types since the trailing period has been bundled with the rest of the word. Although '--' is some kind of token, it's not a word token. Additionally, 'This' and 'this' are incorrectly distinguished from each other, because of a difference in capitalization that should be ignored.
If we turn to languages other than English, tokenizing text is even more challenging. In Chinese text there is no visual representation of word boundaries. Consider the following three-character string: 爱国人 (in pinyin plus tones: ai4 "love" (verb), guo3 "country", ren2 "person"). This could either be segmented as [爱国]人, "country-loving person" or as 爱[国人], "love country-person."
The terms token and type can also be applied to other linguistic entities. For example, a sentence token is an individual occurrence of a sentence; but a sentence type is an abstract sentence, without context. If I say the same sentence twice, I have uttered two sentence tokens but only used one sentence type. When the kind of token or type is obvious from context, we will simply use the terms token and type.
To summarize, we cannot just say that two word tokens have the same type if they are the same string of characters. We need to consider a variety of factors in determining what counts as the same word, and we need to be careful in how we identify tokens in the first place.
Up till now, we have relied on getting our source texts by defining a string in a fragment of Python code. However, this is impractical for all but the simplest of texts, and makes it hard to present realistic examples. So how do we get larger chunks of text into our programs? In the rest of this section, we will see how to extract text from files, from the web, and from the corpora distributed with NLTK.
2.2.1 Extracting Text from Files
It is easy to access local files in Python. As an exercise, create a file called corpus.txt using a text editor, and enter the following text:
Hello World! This is a test file.
Be sure to save the file as plain text. You also need to make sure that you have saved the file in the same directory or folder in which you are running the Python interactive interpreter.
Note
If you are using IDLE, you can easily create this file by selecting the New Window command in the File menu, typing the required text into this window, and then saving the file as corpus.txt in the first directory that IDLE offers in the pop-up dialogue box.
The next step is to open a file using the built-in function open() which takes two arguments, the name of the file, here corpus.txt, and the mode to open the file with ('r' means to open the file for reading, and 'U' stands for "Universal", which lets us ignore the different conventions used for marking newlines).
|
Note
If the interpreter cannot find your file, it will give an error like this:
|
To check that the file that you are trying to open is really in the right directory, use IDLE's Open command in the File menu; this will display a list of all the files in the directory where IDLE is running. An alternative is to examine the current directory from within Python:
|
There are several methods for reading the file. The following uses the method read() on the file object f; this reads the entire contents of a file into a string.
|
Recall that the '\n' characters are newlines; this is equivalent to pressing Enter on a keyboard and starting a new line. Note that we can open and read a file in one step:
|
We can also read a file one line at a time using the for loop construct:
|
Here we use the slice [:-1] to remove the newline character at the end of the input line.
2.2.2 Extracting Text from the Web
Opening a web page is not much different to opening a file, except that we use urlopen():
|
Web pages are usually in HTML format. To extract the text, we need to strip out the HTML markup, i.e. remove all material enclosed in angle brackets. Let's digress briefly to consider how to carry out this task using regular expressions. Our first attempt might look as follows:
|
So the regular expression '<.*>' is intended to match a pair of left and right angle brackets, with a string of any characters intervening. However, look at what the result is:
|
What has happened here? The problem is twofold. First, the wildcard '.' matches any character other than '\n', so it will match '>' and '<'. Second, the '*' operator is "greedy", in the sense that it matches as many characters as it can. In the above example, '.*' will return not the shortest match, namely 'title', but the longest match, 'title>BBC NEWS | News Front Page</title'. To get the shortest match we have to use the '*?' operator. We will also normalize whitespace, replacing any sequence of spaces, tabs or newlines ('\s+') with a single space character.
|
Note
Note that your output for the above code may differ from ours, because the BBC home page may have been changed since this example was created.
You will probably find it useful to borrow the structure of the above code snippet for future tasks involving regular expressions: each time through a series of substitutions, the result of operating on page gets assigned as the new value of page. This approach allows us to decompose the transformations we need into a series of simple regular expression substitutions, each of which can be tested and debugged on its own.
Note
Getting text out of HTML is a sufficiently common task that NLTK provides a helper function nltk.clean_html(), which takes an HTML string and returns text.
2.2.3 Extracting Text from NLTK Corpora
NLTK is distributed with several corpora and corpus samples and many are supported by the corpus package. Here we use a selection of texts from the Project Gutenberg electronic text archive, and list the files it contains:
|
We can count the number of tokens for each text in our Gutenberg sample as follows:
|
Note
It is possible to use the methods described in section 2.2.1 along with nltk.data.find() method to access and read the corpus files directly. The method described in this section is superior since it takes care of tokenization and conveniently skips over the Gutenberg file header.
But note that this has several disadvantages. The ones that come to mind immediately are: (i) The corpus reader automatically strips out the Gutenberg header; this version doesn't. (ii) The corpus reader uses a somewhat smarter method to break lines into words; this version just splits on whitespace. (iii) Using the corpus reader, you can also access the documents by sentence or paragraph; doing that by hand, you'd need to do some extra work.
The Brown Corpus was the first million-word, part-of-speech tagged electronic corpus of English, created in 1961 at Brown University. Each of the sections a through r represents a different genre, as shown in Table 2.1.
| Sec | Genre | Sec | Genre | Sec | Genre |
|---|---|---|---|---|---|
| a | Press: Reportage | b | Press: Editorial | c | Press: Reviews |
| d | Religion | e | Skill and Hobbies | f | Popular Lore |
| g | Belles-Lettres | h | Government | j | Learned |
| k | Fiction: General | k | Fiction: General | l | Fiction: Mystery |
| m | Fiction: Science | n | Fiction: Adventure | p | Fiction: Romance |
| r | Humor |
We can access the corpus as a list of words, or a list of sentences (where each sentence is itself just a list of words). We can optionally specify a section of the corpus to read:
|
NLTK comes with corpora for many languages, though in some cases you will need to learn how to manipulate character encodings in Python before using these corpora.
|
Before concluding this section, we return to the original topic of distinguishing tokens and types. Now that we can access substantial quantities of text, we will give a preview of the interesting computations we will be learning how to do (without yet explaining all the details). Listing 2.1 computes vocabulary growth curves for US Presidents, shown in Figure 2.1 (a color figure in the online version). These curves show the number of word types seen after n word tokens have been read.
Note
Listing 2.1 uses the PyLab package which supports sophisticated plotting functions with a MATLAB-style interface. For more information about this package please see http://matplotlib.sourceforge.net/. The listing also uses the yield statement, which will be explained in Chapter 5.
| ||
| ||
Listing 2.1 (vocabulary_growth.py): Vocabulary Growth in State-of-the-Union Addresses |
Figure 2.1: Vocabulary Growth in State-of-the-Union Addresses
2.2.4 Exercises
- ☼ Create a small text file, and write a program to read it and print it with a line number at the start of each line. (Make sure you don't introduce an extra blank line between each line.)
- ☼ Use the corpus module to read austen-persuasion.txt. How many word tokens does this book have? How many word types?
- ☼ Use the Brown corpus reader nltk.corpus.brown.words() or the Web text corpus reader nltk.corpus.webtext.words() to access some sample text in two different genres.
- ☼ Use the Brown corpus reader nltk.corpus.brown.sents() to find sentence-initial examples of the word however. Check whether these conform to Strunk and White's prohibition against sentence-initial however used to mean "although".
- ☼ Read in the texts of the State of the Union addresses, using the state_union corpus reader. Count occurrences of men, women, and people in each document. What has happened to the usage of these words over time?
- ◑ Write code to read a file and print the lines in reverse order, so that the last line is listed first.
- ◑ Read in some text from a corpus, tokenize it, and print the list of all wh-word types that occur. (wh-words in English are used in questions, relative clauses and exclamations: who, which, what, and so on.) Print them in order. Are any words duplicated in this list, because of the presence of case distinctions or punctuation?
- ◑ Write code to access a favorite webpage and extract some text from it. For example, access a weather site and extract the forecast top temperature for your town or city today.
- ◑ Write a function unknown() that takes a URL as its argument, and returns a list of unknown words that occur on that webpage. In order to do this, extract all substrings consisting of lowercase letters (using re.findall()) and remove any items from this set that occur in the words corpus (nltk.corpus.words). Try to categorize these words manually and discuss your findings.
- ◑ Examine the results of processing the URL http://news.bbc.co.uk/ using the regular expressions suggested above. You will see that there is still a fair amount of non-textual data there, particularly Javascript commands. You may also find that sentence breaks have not been properly preserved. Define further regular expressions that improve the extraction of text from this web page.
- ◑ Take a copy of the http://news.bbc.co.uk/ over three different days, say at two-day intervals. This should give you three different files, bbc1.txt, bbc2.txt and bbc3.txt, each corresponding to a different snapshot of world events. Collect the 100 most frequent word tokens for each file. What can you tell from the changes in frequency?
- ◑ Define a function ghits() that takes a word as its argument and builds a Google query string of the form http://www.google.com/search?q=word. Strip the HTML markup and normalize whitespace. Search for a substring of the form Results 1 - 10 of about, followed by some number n, and extract n. Convert this to an integer and return it.
- ◑ Try running the various chatbots included with NLTK, using nltk.chat.demo(). How intelligent are these programs? Take a look at the program code and see if you can discover how it works. You can find the code online at: http://nltk.org/nltk/chat/.
- ★ Define a function find_language() that takes a string as its argument, and returns a list of languages that have that string as a word. Use the udhr corpus and limit your searches to files in the Latin-1 encoding.
2.3 Tokenization and Normalization
Tokenization, as we saw, is the task of extracting a sequence of elementary tokens that constitute a piece of language data. In our first attempt to carry out this task, we started off with a string of characters, and used the split() method to break the string at whitespace characters. Recall that "whitespace" covers not only inter-word space, but also tabs and newlines. We pointed out that tokenization based solely on whitespace is too simplistic for most applications. In this section we will take a more sophisticated approach, using regular expressions to specify which character sequences should be treated as words. We will also look at ways to normalize tokens.
2.3.1 Tokenization with Regular Expressions
The function nltk.tokenize.regexp_tokenize() takes a text string and a regular expression, and returns the list of substrings that match the regular expression. To define a tokenizer that includes punctuation as separate tokens, we could do the following:
|
The regular expression in this example will match a sequence consisting of one or more word characters \w+. It will also match a sequence consisting of one or more punctuation characters (or non-word, non-space characters [^\w\s]+). This is another negated range expression; it matches one or more characters that are not word characters (i.e., not a match for \w) and not a whitespace character (i.e., not a match for \s). We use the disjunction operator | to combine these into a single complex expression \w+|[^\w\s]+.
There are a number of ways we could improve on this regular expression. For example, it currently breaks $22.50 into four tokens; we might want it to treat this as a single token. Similarly, U.S.A. should count as a single token. We can deal with these by adding further cases to the regular expression. For readability we will break it up and insert comments, and insert the special (?x) "verbose flag" so that Python knows to strip out the embedded whitespace and comments.
|
It is sometimes more convenient to write a regular expression matching the material that appears between tokens, such as whitespace and punctuation. The nltk.tokenize.regexp_tokenize() function permits an optional boolean parameter gaps; when set to True the pattern is matched against the gaps. For example, we could define a whitespace tokenizer as follows:
|
It is more convenient to call NLTK's whitespace tokenizer directly, as nltk.WhitespaceTokenizer(text). (However, in this case is generally better to use Python's split() method, defined on strings: text.split().)
2.3.2 Lemmatization and Normalization
Earlier we talked about counting word tokens, and completely ignored the rest of the sentence in which these tokens appeared. Thus, for an example like I saw the saw, we would have treated both saw tokens as instances of the same type. However, one is a form of the verb see, and the other is the name of a cutting instrument. How do we know that these two forms of saw are unrelated? One answer is that as speakers of English, we know that these would appear as different entries in a dictionary. Another, more empiricist, answer is that if we looked at a large enough number of texts, it would become clear that the two forms have very different distributions. For example, only the noun saw will occur immediately after determiners such as the. Distinct words that have the same written form are called homographs. We can distinguish homographs with the help of context; often the previous word suffices. We will explore this idea of context briefly, before addressing the main topic of this section.
As a first approximation to discovering the distribution of a word, we can look at all the bigrams it occurs in. A bigram is simply a pair of words. For example, in the sentence She sells sea shells by the sea shore, the bigrams are She sells, sells sea, sea shells, shells by, by the, the sea, sea shore. Let's consider all bigrams from the Brown Corpus that have the word often as first element. Here is a small selection, ordered by their counts:
often , 16 often a 10 often in 8 often than 7 often the 7 often been 6 often do 5 often called 4 often appear 3 often were 3 often appeared 2 often are 2 often did 2 often is 2 often appears 1 often call 1
In the topmost entry, we see that often is frequently followed by a comma. This suggests that often is common at the end of phrases. We also see that often precedes verbs, presumably as an adverbial modifier. We might conclude that when saw appears in the context often saw, then saw is being used as a verb.
You will also see that this list includes different grammatical forms of the same verb. We can form separate groups consisting of appear ~ appears ~ appeared; call ~ called; do ~ did; and been ~ were ~ are ~ is. It is common in linguistics to say that two forms such as appear and appeared belong to a more abstract notion of a word called a lexeme; by contrast, appeared and called belong to different lexemes. You can think of a lexeme as corresponding to an entry in a dictionary, and a lemma as the headword for that entry. By convention, small capitals are used when referring to a lexeme or lemma: appear.
Although appeared and called belong to different lexemes, they do have something in common: they are both past tense forms. This is signaled by the segment -ed, which we call a morphological suffix. We also say that such morphologically complex forms are inflected. If we strip off the suffix, we get something called the stem, namely appear and call respectively. While appeared, appears and appearing are all morphologically inflected, appear lacks any morphological inflection and is therefore termed the base form. In English, the base form is conventionally used as the lemma for a word.
Our notion of context would be more compact if we could group different forms of the various verbs into their lemmas; then we could study which verb lexemes are typically modified by a particular adverb. Lemmatization — the process of mapping words to their lemmas — would yield the following picture of the distribution of often. Here, the counts for often appear (3), often appeared (2) and often appears (1) are combined into a single line.
often , 16 often a 10 often be 13 often in 8 often than 7 often the 7 often do 7 often appear 6 often call 5
Lemmatization is a rather sophisticated process that uses rules for the regular word patterns, and table look-up for the irregular patterns. Within NLTK, we can use off-the-shelf stemmers, such as the Porter Stemmer, the Lancaster Stemmer, and the stemmer that comes with WordNet, e.g.:
|
Stemmers for other languages are added to NLTK as they are contributed, e.g. the RSLP Portuguese Stemmer, nltk.RSLPStemmer().
Lemmatization and stemming are special cases of normalization. They identify a canonical representative for a set of related word forms. Normalization collapses distinctions. Exactly how we normalize words depends on the application. Often, we convert everything into lower case so that we can ignore the written distinction between sentence-initial words and the rest of the words in the sentence. The Python string method lower() will accomplish this for us:
|
A final issue for normalization is the presence of contractions, such as didn't. If we are analyzing the meaning of a sentence, it would probably be more useful to normalize this form to two separate forms: did and n't (or not).
2.3.3 Transforming Lists
Lemmatization and normalization involve applying the same operation to each word token in a text. List comprehensions are a convenient Python construct for doing this. Here we lowercase each word:
|
A list comprehension usually has the form [item.foo() for item in sequence], or [foo(item) for item in sequence]. It creates a list but applying an operation to every item in the supplied sequence. Here we rewrite the loop for identifying verb stems that we saw in the previous section:
|
Now we can eliminate repeats using set(), by passing the list comprehension as an argument. We can actually leave out the square brackets, as will be explained further in Chapter 9.
|
This syntax might be reminiscent of the notation used for building sets, e.g. {(x,y) | x2 + y2 = 1}. (We will return to sets later in Section 9). Just as this set definition incorporates a constraint, list comprehensions can constrain the items they include. In the next example we remove some non-content words from a list of words:
|
Now we can combine the two ideas (constraints and normalization), to pull out the content words and normalize them.
|
List comprehensions can build nested structures too. For example, the following code builds a list of tuples, where each tuple consists of a word and its stem.
|
2.3.4 Sentence Segmentation
Manipulating texts at the level of individual words often presupposes the ability to divide a text into individual sentences. As we have seen, some corpora already provide access at the sentence level. In the following example, we compute the average number of words per sentence in the Brown Corpus:
|
In other cases, the text is only available as a stream of characters. Before doing word tokenization, we need to do sentence segmentation. NLTK facilitates this by including the Punkt sentence segmenter [Tibor & Jan, 2006], along with supporting data for English. Here is an example of its use in segmenting the text of a novel:
|
Notice that this example is really a single sentence, reporting the speech of Mr Lucian Gregory. However, the quoted speech contains several sentences, and these have been split into individual strings. This is reasonable behavior for most applications.
2.3.5 Exercises
☼ Regular expression tokenizers: Save some text into a file corpus.txt. Define a function load(f) that reads from the file named in its sole argument, and returns a string containing the text of the file.
- Use nltk.tokenize.regexp_tokenize() to create a tokenizer that tokenizes the various kinds of punctuation in this text. Use a single regular expression, with inline comments using the re.VERBOSE flag.
- Use nltk.tokenize.regexp_tokenize() to create a tokenizer that tokenizes the following kinds of expression: monetary amounts; dates; names of people and companies.
☼ Rewrite the following loop as a list comprehension:
>>> sent = ['The', 'dog', 'gave', 'John', 'the', 'newspaper'] >>> result = [] >>> for word in sent: ... word_len = (word, len(word)) ... result.append(word_len) >>> result [('The', 3), ('dog', 3), ('gave', 4), ('John', 4), ('the', 3), ('newspaper', 9)]
◑ Use the Porter Stemmer to normalize some tokenized text, calling the stemmer on each word. Do the same thing with the Lancaster Stemmer and see if you observe any differences.
◑ Consider the numeric expressions in the following sentence from the MedLine corpus: The corresponding free cortisol fractions in these sera were 4.53 +/- 0.15% and 8.16 +/- 0.23%, respectively. Should we say that the numeric expression 4.53 +/- 0.15% is three words? Or should we say that it's a single compound word? Or should we say that it is actually nine words, since it's read "four point five three, plus or minus fifteen percent"? Or should we say that it's not a "real" word at all, since it wouldn't appear in any dictionary? Discuss these different possibilities. Can you think of application domains that motivate at least two of these answers?
◑ Readability measures are used to score the reading difficulty of a text, for the purposes of selecting texts of appropriate difficulty for language learners. Let us define μw to be the average number of letters per word, and μs to be the average number of words per sentence, in a given text. The Automated Readability Index (ARI) of the text is defined to be: 4.71 * `` |mu|\ :subscript:`w` ``+ 0.5 * `` |mu|\ :subscript:`s` ``- 21.43. Compute the ARI score for various sections of the Brown Corpus, including section f (popular lore) and j (learned). Make use of the fact that nltk.corpus.brown.words() produces a sequence of words, while nltk.corpus.brown.sents() produces a sequence of sentences.
★ Obtain raw texts from two or more genres and compute their respective reading difficulty scores as in the previous exercise. E.g. compare ABC Rural News and ABC Science News (nltk.corpus.abc). Use Punkt to perform sentence segmentation.
★ Rewrite the following nested loop as a nested list comprehension:
>>> words = ['attribution', 'confabulation', 'elocution', ... 'sequoia', 'tenacious', 'unidirectional'] >>> vsequences = set() >>> for word in words: ... vowels = [] ... for char in word: ... if char in 'aeiou': ... vowels.append(char) ... vsequences.add(''.join(vowels)) >>> sorted(vsequences) ['aiuio', 'eaiou', 'eouio', 'euoia', 'oauaio', 'uiieioa']
2.4 Counting Words: Several Interesting Applications
Now that we can count words (tokens or types), we can write programs to perform a variety of useful tasks, to study stylistic differences in language use, differences between languages, and even to generate random text.
Before getting started, we need to see how to get Python to count the number of occurrences of each word in a document.
In line ![[1]](callouts/callout1.gif) we initialize the dictionary.
Then for each word in each sentence we increment a counter (line
we initialize the dictionary.
Then for each word in each sentence we increment a counter (line ![[2]](callouts/callout2.gif) ).
To view the contents of the dictionary, we can iterate over its keys and print
each entry (here just for the first 5 entries, line
).
To view the contents of the dictionary, we can iterate over its keys and print
each entry (here just for the first 5 entries, line ![[3]](callouts/callout3.gif) ).
).
2.4.1 Frequency Distributions
This style of output and our counts object are just different forms of the same abstract structure — a collection of items and their frequencies — known as a frequency distribution. Since we will often need to count things, NLTK provides a FreqDist() class. We can write the same code more conveniently as follows:
|
Some of the methods defined on NLTK frequency distributions are shown in Table 2.2.
| Name | Sample | Description |
|---|---|---|
| Count | fd['the'] | number of times a given sample occurred |
| Frequency | fd.freq('the') | frequency of a given sample |
| N | fd.N() | number of samples |
| Samples | list(fd) | list of distinct samples recorded (also fd.keys()) |
| Max | fd.max() | sample with the greatest number of outcomes |
This output isn't very interesting. Perhaps it would be more informative to list the most frequent word tokens first. Now a FreqDist object is just a kind of dictionary, so we can easily get its key-value pairs and sort them by decreasing values, as follows:
|
Note the arguments of the sorted() function (line ![[1]](callouts/callout1.gif) ): itemgetter(1)
returns a function that can be called on any sequence object to return the item at position 1;
reverse=True performs the sort in reverse order. Together, these ensure that the
word with the highest frequency is listed first. This reversed sort by frequency is
such a common requirement that it is built into the FreqDist object.
Listing 2.2 demonstrates this, and also prints rank and cumulative frequency.
): itemgetter(1)
returns a function that can be called on any sequence object to return the item at position 1;
reverse=True performs the sort in reverse order. Together, these ensure that the
word with the highest frequency is listed first. This reversed sort by frequency is
such a common requirement that it is built into the FreqDist object.
Listing 2.2 demonstrates this, and also prints rank and cumulative frequency.
| ||
| ||
Listing 2.2 (print_freq.py): Words and Cumulative Frequencies, in Order of Decreasing Frequency |
Unfortunately the output in Listing 2.2 is surprisingly dull. A mere handful of tokens account for a third of the text. They just represent the plumbing of English text, and are completely uninformative! How can we find words that are more indicative of a text? As we will see in the exercises for this section, we can modify the program to discard the non-content words. In the next section we see another approach.
2.4.2 Stylistics
Stylistics is a broad term covering literary genres and varieties of language use. Here we will look at a document collection that is categorized by genre, and try to learn something about the patterns of word usage. For example, Table 2.3 was constructed by counting the number of times various modal words appear in different sections of the corpus:
| Genre | can | could | may | might | must | will |
|---|---|---|---|---|---|---|
| skill and hobbies | 273 | 59 | 130 | 22 | 83 | 259 |
| humor | 17 | 33 | 8 | 8 | 9 | 13 |
| fiction: science | 16 | 49 | 4 | 12 | 8 | 16 |
| press: reportage | 94 | 86 | 66 | 36 | 50 | 387 |
| fiction: romance | 79 | 195 | 11 | 51 | 46 | 43 |
| religion | 84 | 59 | 79 | 12 | 54 | 64 |
Observe that the most frequent modal in the reportage genre is will, suggesting a focus on the future, while the most frequent modal in the romance genre is could, suggesting a focus on possibilities.
We can also measure the lexical diversity of a genre, by calculating the ratio of word types and word tokens, as shown in Table 2.4. Genres with lower diversity have a higher number of tokens per type, thus we see that humorous prose is almost twice as lexically diverse as romance prose.
| Genre | Token Count | Type Count | Ratio |
|---|---|---|---|
| skill and hobbies | 82345 | 11935 | 6.9 |
| humor | 21695 | 5017 | 4.3 |
| fiction: science | 14470 | 3233 | 4.5 |
| press: reportage | 100554 | 14394 | 7.0 |
| fiction: romance | 70022 | 8452 | 8.3 |
| religion | 39399 | 6373 | 6.2 |
We can carry out a variety of interesting explorations simply by counting words. In fact, the field of Corpus Linguistics focuses heavily on creating and interpreting such tables of word counts.
2.4.3 Aside: Defining Functions
It often happens that part of a program needs to be used several times over. For example, suppose we were writing a program that needed to be able to form the plural of a singular noun, and that this needed to be done at various places during the program. Rather than repeating the same code several times over, it is more efficient (and reliable) to localize this work inside a function. A function is a programming construct that can be called with one or more inputs and which returns an output. We define a function using the keyword def followed by the function name and any input parameters, followed by a colon; this in turn is followed by the body of the function. We use the keyword return to indicate the value that is produced as output by the function. The best way to convey this is with an example. Our function plural() in Listing 2.3 takes a singular noun and generates a plural form (one which is not always correct).
| ||
| ||
Listing 2.3 (plural.py): Example of a Python function |
(There is much more to be said about ways of defining functions, but we will defer this until Section 5.4.)
2.4.4 Lexical Dispersion
Word tokens vary in their distribution throughout a text. We can visualize word distributions to get an overall sense of topics and topic shifts. For example, consider the pattern of mention of the main characters in Jane Austen's Sense and Sensibility: Elinor, Marianne, Edward and Willoughby. The following plot contains four rows, one for each name, in the order just given. Each row contains a series of lines, drawn to indicate the position of each token.

Figure 2.2: Lexical Dispersion Plot for the Main Characters in Sense and Sensibility
As you can see, Elinor and Marianne appear rather uniformly throughout the text, while Edward and Willoughby tend to appear separately. Here is the code that generated the above plot.
|
2.4.5 Comparing Word Lengths in Different Languages
We can use a frequency distribution to examine the distribution of word lengths in a corpus. For each word, we find its length, and increment the count for words of this length.
|
Now we can call print_length_dist on a text to print the distribution of word lengths. We see that the most frequent word length for the English sample is 3 characters, while the most frequent length for the Finnish sample is 5-6 characters.
|
This is an intriguing area for exploration, and so in Listing 2.4 we look at it on a larger scale using the Universal Declaration of Human Rights corpus, which has text samples from over 300 languages. (Note that the names of the files in this corpus include information about character encoding; here we will use texts in ISO Latin-1.) The output is shown in Figure 2.3 (a color figure in the online version).
| ||
| ||
Listing 2.4 (word_len_dist.py): Cumulative Word Length Distributions for Several Languages |
Figure 2.3: Cumulative Word Length Distributions for Several Languages
2.4.6 Generating Random Text with Style
We have used frequency distributions to count the number of occurrences of each word in a text. Here we will generalize this idea to look at the distribution of words in a given context. A conditional frequency distribution is a collection of frequency distributions, each one for a different condition. Here the condition will be the preceding word.
In Listing 2.5, we've defined a function train_model() that uses ConditionalFreqDist() to count words as they appear relative to the context defined by the preceding word (stored in prev). It scans the corpus, incrementing the appropriate counter, and updating the value of prev. The function generate_model() contains a simple loop to generate text: we set an initial context, pick the most likely token in that context as our next word (using max()), and then use that word as our new context. This simple approach to text generation tends to get stuck in loops; another method would be to randomly choose the next word from among the available words.
| ||
| ||
Listing 2.5 (random.py): Generating Random Text in the Style of Genesis |
2.4.7 Collocations
Collocations are pairs of content words that occur together more often than one would expect if the words of a document were scattered randomly. We can find collocations by counting how many times a pair of words w1, w2 occurs together, compared to the overall counts of these words (this program uses a heuristic related to the mutual information measure, http://www.collocations.de/) In Listing 2.6 we try this for the files in the webtext corpus.
| ||
| ||
Listing 2.6 (collocations.py): A Simple Program to Find Collocations |
2.4.8 Exercises
☺ Compare the lexical dispersion plot with Google Trends, which shows the frequency with which a term has been referenced in news reports or been used in search terms over time.
☼ Pick a text, and explore the dispersion of particular words. What does this tell you about the words, or the text?
☼ The program in Listing 2.2 used a dictionary of word counts. Modify the code that creates these word counts so that it ignores non-content words. You can easily get a list of words to ignore with:
>>> ignored_words = nltk.corpus.stopwords.words('english')
☼ Modify the generate_model() function in Listing 2.5 to use Python's random.choose() method to randomly pick the next word from the available set of words.
☼ The demise of teen language: Read the BBC News article: UK's Vicky Pollards 'left behind' http://news.bbc.co.uk/1/hi/education/6173441.stm. The article gives the following statistic about teen language: "the top 20 words used, including yeah, no, but and like, account for around a third of all words." Use the program in Listing 2.2 to find out how many word types account for a third of all word tokens, for a variety of text sources. What do you conclude about this statistic? Read more about this on LanguageLog, at http://itre.cis.upenn.edu/~myl/languagelog/archives/003993.html.
◑ Write a program to find all words that occur at least three times in the Brown Corpus.
◑ Write a program to generate a table of token/type ratios, as we saw in Table 2.4. Include the full set of Brown Corpus genres (nltk.corpus.brown.categories()). Which genre has the lowest diversity (greatest number of tokens per type)? Is this what you would have expected?
◑ Modify the text generation program in Listing 2.5 further, to do the following tasks:
- Store the n most likely words in a list lwords then randomly choose a word from the list using random.choice().
- Select a particular genre, such as a section of the Brown Corpus, or a genesis translation, one of the Gutenberg texts, or one of the Web texts. Train the model on this corpus and get it to generate random text. You may have to experiment with different start words. How intelligible is the text? Discuss the strengths and weaknesses of this method of generating random text.
- Now train your system using two distinct genres and experiment with generating text in the hybrid genre. Discuss your observations.
◑ Write a program to print the most frequent bigrams (pairs of adjacent words) of a text, omitting non-content words, in order of decreasing frequency.
◑ Write a program to create a table of word frequencies by genre, like the one given above for modals. Choose your own words and try to find words whose presence (or absence) is typical of a genre. Discuss your findings.
◑ Zipf's Law: Let f(w) be the frequency of a word w in free text. Suppose that all the words of a text are ranked according to their frequency, with the most frequent word first. Zipf's law states that the frequency of a word type is inversely proportional to its rank (i.e. f.r = k, for some constant k). For example, the 50th most common word type should occur three times as frequently as the 150th most common word type.
- Write a function to process a large text and plot word frequency against word rank using pylab.plot. Do you confirm Zipf's law? (Hint: it helps to use a logarithmic scale). What is going on at the extreme ends of the plotted line?
- Generate random text, e.g. using random.choice("abcdefg "), taking care to include the space character. You will need to import random first. Use the string concatenation operator to accumulate characters into a (very) long string. Then tokenize this string, and generate the Zipf plot as before, and compare the two plots. What do you make of Zipf's Law in the light of this?
◑ Exploring text genres: Investigate the table of modal distributions and look for other patterns. Try to explain them in terms of your own impressionistic understanding of the different genres. Can you find other closed classes of words that exhibit significant differences across different genres?
◑ Write a function tf() that takes a word and the name of a section of the Brown Corpus as arguments, and computes the text frequency of the word in that section of the corpus.
★ Authorship identification: Reproduce some of the results of [Zhao & Zobel, 2007].
★ Gender-specific lexical choice: Reproduce some of the results of http://www.clintoneast.com/articles/words.php
2.5 WordNet: An English Lexical Database
WordNet is a semantically-oriented dictionary of English, similar to a traditional thesaurus but with a richer structure. WordNet groups words into synonym sets, or synsets, each with its own definition and with links to other synsets. WordNet 3.0 data is distributed with NLTK, and includes 117,659 synsets.
Although WordNet was originally developed for research in psycholinguistics, it is widely used in NLP and Information Retrieval. WordNets are being developed for many other languages, as documented at http://www.globalwordnet.org/.
2.5.1 Senses and Synonyms
Consider the following sentence:
| (2) | Benz is credited with the invention of the motorcar. |
If we replace motorcar in (2) by automobile, the meaning of the sentence stays pretty much the same:
| (3) | Benz is credited with the invention of the automobile. |
Since everything else in the sentence has remained unchanged, we can conclude that the words motorcar and automobile have the same meaning, i.e. they are synonyms.
In order to look up the senses of a word, we need to pick a part of speech for the word. WordNet contains four dictionaries: N (nouns), V (verbs), ADJ (adjectives), and ADV (adverbs). To simplify our discussion, we will focus on the N dictionary here. Let's look up motorcar in the N dictionary.
|
The variable car is now bound to a Word object. Words will often have more than sense, where each sense is represented by a synset. However, motorcar only has one sense in WordNet, as we can discover using len(). We can then find the synset (a set of lemmas), the words it contains, and a gloss.
|
The wordnet module also defines Synsets. Let's look at a word which is polysemous; that is, which has multiple synsets:
|
2.5.2 The WordNet Hierarchy
WordNet synsets correspond to abstract concepts, which may or may not have corresponding words in English. These concepts are linked together in a hierarchy. Some are very general, such as Entity, State, Event — these are called unique beginners. Others, such as gas guzzler and hatchback, are much more specific. A small portion of a concept hierarchy is illustrated in Figure 2.4. The edges between nodes indicate the hypernym/hyponym relation; the dotted line at the top is intended to indicate that artifact is a non-immediate hypernym of motorcar.

Figure 2.4: Fragment of WordNet Concept Hierarchy
WordNet makes it easy to navigate between concepts. For example, given a concept like motorcar, we can look at the concepts that are more specific; the (immediate) hyponyms. Here is one way to carry out this navigation:
|
We can also move up the hierarchy, by looking at broader concepts than motorcar, e.g. the immediate hypernym of a concept:
|
We can also look for the hypernyms of hypernyms. In fact, from any synset we can trace (multiple) paths back to a unique beginner. Synsets have a method for doing this, called tree(), which produces a nested list structure.
|
A related method closure() produces a flat version of this structure, with repeats eliminated. Both of these functions take an optional depth argument that permits us to limit the number of steps to take. (This is important when using unbounded relations like SIMILAR.) Table 2.5 lists the most important lexical relations supported by WordNet; see dir(wordnet) for a full list.
| Hypernym | more general | animal is a hypernym of dog |
| Hyponym | more specific | dog is a hyponym of animal |
| Meronym | part of | door is a meronym of house |
| Holonym | has part | house is a holonym of door |
| Synonym | similar meaning | car is a synonym of automobile |
| Antonym | opposite meaning | like is an antonym of dislike |
| Entailment | necessary action | step is an entailment of walk |
Recall that we can iterate over the words of a synset, with for word in synset. We can also test if a word is in a dictionary, e.g. if word in wordnet.V. As our last task, let's put these together to find "animal words" that are used as verbs. Since there are a lot of these, we will cut this off at depth 4. Can you think of the animal and verb sense of each word?
|
NLTK also includes VerbNet, a hierarhical verb lexicon linked to WordNet. It can be accessed with nltk.corpus.verbnet.
2.5.3 WordNet Similarity
We would expect that the semantic similarity of two concepts would correlate with the length of the path between them in WordNet. The wordnet package includes a variety of measures that incorporate this basic insight. For example, path_similarity assigns a score in the range 0–1, based on the shortest path that connects the concepts in the hypernym hierarchy (-1 is returned in those cases where a path cannot be found). A score of 1 represents identity, i.e., comparing a sense with itself will return 1.
|
Several other similarity measures are provided in wordnet: Leacock-Chodorow, Wu-Palmer, Resnik, Jiang-Conrath, and Lin. For a detailed comparison of various measures, see [Budanitsky & Hirst, 2006].
2.5.4 Exercises
- ☼ Familiarize yourself with the WordNet interface, by reading the documentation available via help(wordnet). Try out the text-based browser, wordnet.browse().
- ☼ Investigate the holonym / meronym relations for some nouns. Note that there are three kinds (member, part, substance), so access is more specific, e.g., wordnet.MEMBER_MERONYM, wordnet.SUBSTANCE_HOLONYM.
- ☼ The polysemy of a word is the number of senses it has. Using WordNet, we can determine that the noun dog has 7 senses with: len(nltk.wordnet.N['dog']). Compute the average polysemy of nouns, verbs, adjectives and adverbs according to WordNet.
- ◑ What is the branching factor of the noun hypernym hierarchy? (For all noun synsets that have hyponyms, how many do they have on average?)
- ◑ Define a function supergloss(s) that takes a synset s as its argument and returns a string consisting of the concatenation of the glosses of s, all hypernyms of s, and all hyponyms of s.
- ◑ Write a program to score the similarity of two nouns as the depth of their first common hypernym.
- ★ Use one of the predefined similarity measures to score the similarity of each of the following pairs of words. Rank the pairs in order of decreasing similarity. How close is your ranking to the order given here? (Note that this order was established experimentally by [Miller & Charles, 1998].)
- ::
- car-automobile, gem-jewel, journey-voyage, boy-lad, coast-shore, asylum-madhouse, magician-wizard, midday-noon, furnace-stove, food-fruit, bird-cock, bird-crane, tool-implement, brother-monk, lad-brother, crane-implement, journey-car, monk-oracle, cemetery-woodland, food-rooster, coast-hill, forest-graveyard, shore-woodland, monk-slave, coast-forest, lad-wizard, chord-smile, glass-magician, rooster-voyage, noon-string.
- ★ Write a program that processes a text and discovers cases where a word has been used with a novel sense. For each word, compute the wordnet similarity between all synsets of the word and all synsets of the words in its context. (Note that this is a crude approach; doing it well is an open research problem.)
2.6 Conclusion
In this chapter we saw that we can do a variety of interesting language processing tasks that focus solely on words. Tokenization turns out to be far more difficult than expected. No single solution works well across-the-board, and we must decide what counts as a token depending on the application domain. We also looked at normalization (including lemmatization) and saw how it collapses distinctions between tokens. In the next chapter we will look at word classes and automatic tagging.
2.7 Summary
- we can read text from a file f using text = open(f).read()
- we can read text from a URL u using text = urlopen(u).read()
- NLTK comes with many corpora, e.g. the Brown Corpus, corpus.brown.
- a word token is an individual occurrence of a word in a particular context
- a word type is the vocabulary item, independent of any particular use of that item
- tokenization is the segmentation of a text into basic units — or tokens — such as words and punctuation.
- tokenization based on whitespace is inadequate for many applications because it bundles punctuation together with words
- lemmatization is a process that maps the various forms of a word (such as appeared, appears) to the canonical or citation form of the word, also known as the lexeme or lemma (e.g. appear).
- a frequency distribution is a collection of items along with their frequency counts (e.g. the words of a text and their frequency of appearance).
- WordNet is a semantically-oriented dictionary of English, consisting of synonym sets — or synsets — and organized into a hierarchical network.
2.8 Further Reading
For a more extended treatment of regular expressions, see A. To learn about Unicode, see B.
For more examples of processing words with NLTK, please see the guides at http://nltk.org/doc/guides/tokenize.html, http://nltk.org/doc/guides/stem.html, and http://nltk.org/doc/guides/wordnet.html. A guide on accessing NLTK corpora is available at: http://nltk.org/doc/guides/corpus.html. Chapters 2 and 3 of [Jurafsky & Martin, 2008] contain more advanced material on regular expressions and morphology.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
3 Categorizing and Tagging Words
3.1 Introduction
In Chapter 2 we dealt with words in their own right. We looked at the distribution of often, identifying the words that follow it; we noticed that often frequently modifies verbs. In fact, it is a member of a whole class of verb-modifying words, the adverbs. Before we delve into this terminology, let's write a program that takes a word and finds other words that appear in the same context (Listing 3.1). For example, given the word woman, the program will find all contexts where woman appears in the corpus, such as the woman saw, then searches for other words that appear in those contexts.
When we run dist_sim() on a few words, we find other words having similar distribution: searching for woman finds man and several other nouns; searching for bought finds verbs; searching for over finds prepositions; searching for the finds determiners. These labels — which may be familiar from grammar lessons — are not just terms invented by grammarians, but labels for groups of words that arise directly from the text. These groups of words are so important that they have several names, all in common use: word classes, lexical categories, and parts of speech. We'll use these names interchangeably.
| ||
| ||
Listing 3.1 (dist_sim.py): Program for Distributional Similarity |
One of the notable features of the Brown corpus is that all the words have been tagged for their part-of-speech. Now, instead of just looking at the words that immediately follow often, we can look at the part-of-speech tags (or POS tags). Table 3.1 lists the top eight, ordered by frequency, along with explanations of each tag. As we can see, the majority of words following often are verbs.
| Tag | Freq | Example | Comment |
|---|---|---|---|
| vbn | 61 | burnt, gone | verb: past participle |
| vb | 51 | make, achieve | verb: base form |
| vbd | 36 | saw, looked | verb: simple past tense |
| jj | 30 | ambiguous, acceptable | adjective |
| vbz | 24 | sees, goes | verb: third-person singular present |
| in | 18 | by, in | preposition |
| at | 18 | a, this | article |
| , | 16 | , | comma |
The process of classifying words into their parts-of-speech and labeling them accordingly is known as part-of-speech tagging, POS-tagging, or simply tagging. The collection of tags used for a particular task is known as a tag set. Our emphasis in this chapter is on exploiting tags, and tagging text automatically.
Automatic tagging has several applications. We have already seen an example of how to exploit tags in corpus analysis — we get a clear understanding of the distribution of often by looking at the tags of adjacent words. Automatic tagging also helps predict the behavior of previously unseen words. For example, if we encounter the word blogging we can probably infer that it is a verb, with the root blog, and likely to occur after forms of the auxiliary to be (e.g. he was blogging). Parts of speech are also used in speech synthesis and recognition. For example, wind/NN, as in the wind blew, is pronounced with a short vowel, whereas wind/VB, as in to wind the clock, is pronounced with a long vowel. Other examples can be found where the stress pattern differs depending on whether the word is a noun or a verb, e.g. contest, insult, present, protest, rebel, suspect. Without knowing the part of speech we cannot be sure of pronouncing the word correctly.
In the next section we will see how to access and explore the Brown Corpus. Following this we will take a closer look at the linguistics of word classes. The rest of the chapter will deal with automatic tagging: simple taggers, evaluation, and n-gram taggers.
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint
3.2 Getting Started with Tagging
Several large corpora, such as the Brown Corpus and portions of the Wall Street Journal, have been tagged for part-of-speech, and we will be able to process this tagged data. Tagged corpus files typically contain text of the following form (this example is from the Brown Corpus):
The/at grand/jj jury/nn commented/vbd on/in a/at number/nn of/in other/ap topics/nns ,/, among/in them/ppo the/at Atlanta/np and/cc Fulton/np-tl County/nn-tl purchasing/vbg departments/nns which/wdt it/pps said/vbd ``/`` are/ber well/ql operated/vbn and/cc follow/vb generally/rb accepted/vbn practices/nns which/wdt inure/vb to/in the/at best/jjt interest/nn of/in both/abx governments/nns ''/'' ./.
Note
The NLTK Brown Corpus reader converts part-of-speech tags to uppercase, as this has become standard practice since the Brown Corpus was published.
3.2.1 Representing Tags and Reading Tagged Corpora
By convention in NLTK, a tagged token is represented using a Python tuple. Python tuples are just like lists, except for one important difference: tuples cannot be changed in place, for example by sort() or reverse(). In other words, like strings, they are immutable. Tuples are formed with the comma operator, and typically enclosed using parentheses. Like lists, tuples can be indexed and sliced:
|
A tagged token is represented using a tuple consisting of just two items. We can create one of these special tuples from the standard string representation of a tagged token, using the function str2tuple():
|
We can construct a list of tagged tokens directly from a string. The first
step is to tokenize the string
to access the individual word/tag strings, and then to convert
each of these into a tuple (using str2tuple()). We do this in
two ways. The first method, starting at line ![[1]](callouts/callout1.gif) , initializes
an empty list tagged_words, loops over the word/tag tokens, converts them into
tuples, appends them to tagged_words, and finally displays the result.
The second method, on line
, initializes
an empty list tagged_words, loops over the word/tag tokens, converts them into
tuples, appends them to tagged_words, and finally displays the result.
The second method, on line ![[2]](callouts/callout2.gif) , uses a list comprehension to do
the same work in a way that is not only more compact, but also more readable.
(List comprehensions were introduced in section 2.3.3).
, uses a list comprehension to do
the same work in a way that is not only more compact, but also more readable.
(List comprehensions were introduced in section 2.3.3).
|
We can access several tagged corpora directly from Python. If a corpus contains tagged text, then it will have a tagged_words() method. Please see the README file included with each corpus for documentation of its tagset.
|
Tagged corpora for several other languages are distributed with NLTK, including Chinese, Hindi, Portuguese, Spanish, Dutch and Catalan. These usually contain non-ASCII text, and Python always displays this in hexadecimal when printing a larger structure such as a list.
|
If your environment is set up correctly, with appropriate editors and fonts, you should be able to display individual strings in a human-readable way. For example, Figure 3.1 shows the output of the demonstration code (nltk.corpus.indian.demo()).

Figure 3.1: POS-Tagged Data from Four Indian Languages
If the corpus is also segmented into sentences, it will have a tagged_sents() method that returns a list of tagged sentences. This will be useful when we come to training automatic taggers, as they typically function on a sentence at a time.
3.2.2 Nouns and Verbs
Linguists recognize several major categories of words in English, such as nouns, verbs, adjectives and determiners. In this section we will discuss the most important categories, namely nouns and verbs.
Nouns generally refer to people, places, things, or concepts, e.g.: woman, Scotland, book, intelligence. Nouns can appear after determiners and adjectives, and can be the subject or object of the verb, as shown in Table 3.2.
| Word | After a determiner | Subject of the verb |
|---|---|---|
| woman | the woman who I saw yesterday ... | the woman sat down |
| Scotland | the Scotland I remember as a child ... | Scotland has five million people |
| book | the book I bought yesterday ... | this book recounts the colonization of Australia |
| intelligence | the intelligence displayed by the child ... | Mary's intelligence impressed her teachers |
Nouns can be classified as common nouns and proper nouns. Proper nouns identify particular individuals or entities, e.g. Moses and Scotland. Common nouns are all the rest. Another distinction exists between count nouns and mass nouns. Count nouns are thought of as distinct entities that can be counted, such as pig (e.g. one pig, two pigs, many pigs). They cannot occur with the word much (i.e. *much pigs). Mass nouns, on the other hand, are not thought of as distinct entities (e.g. sand). They cannot be pluralized, and do not occur with numbers (e.g. *two sands, *many sands). However, they can occur with much (i.e. much sand).
Verbs are words that describe events and actions, e.g. fall, eat in Table 3.3. In the context of a sentence, verbs express a relation involving the referents of one or more noun phrases.
| Word | Simple | With modifiers and adjuncts (italicized) |
|---|---|---|
| fall | Rome fell | Dot com stocks suddenly fell like a stone |
| eat | Mice eat cheese | John ate the pizza with gusto |
Verbs can be classified according to the number of arguments (usually noun phrases) that they require. The word fall is intransitive, requiring exactly one argument (the entity that falls). The word eat is transitive, requiring two arguments (the eater and the eaten). Other verbs are more complex; for instance put requires three arguments, the agent doing the putting, the entity being put somewhere, and a location. We will return to this topic when we come to look at grammars and parsing (see Chapter 7).
In the Brown Corpus, verbs have a range of possible tags, e.g.: give/VB (present), gives/VBZ (present, 3ps), giving/VBG (present continuous; gerund) gave/VBD (simple past), and given/VBN (past participle). We will discuss these tags in more detail in a later section.
3.2.3 Nouns and Verbs in Tagged Corpora
Now that we are able to access tagged corpora, we can write simple programs to garner statistics about the tags. In this section we will focus on the nouns and verbs.
What are the 10 most common verbs? We can write a program to find all words tagged with VB, VBZ, VBG, VBD or VBN.
|
Let's study nouns, and find the most frequent nouns of each noun part-of-speech type. The program in Listing 3.2 finds all tags starting with NN, and provides a few example words for each one. Observe that there are many noun tags; the most important of these have $ for possessive nouns, S for plural nouns (since plural nouns typically end in s), P for proper nouns.
| ||
| ||
Listing 3.2 (findtags.py): Program to Find the Most Frequent Noun Tags |
Some tags contain a plus sign; these are compound tags, and are assigned to words that contain two parts normally treated separately. Some tags contain a minus sign; this indicates disjunction.
3.2.4 The Default Tagger
The simplest possible tagger assigns the same tag to each token. This may seem to be a rather banal step, but it establishes an important baseline for tagger performance. In order to get the best result, we tag each word with the most likely word. (This kind of tagger is known as a majority class classifier). What then, is the most frequent tag? We can find out using a simple program:
|
Now we can create a tagger, called default_tagger, that tags everything as NN.
|
This is a simple algorithm, and it performs poorly when used on its own. On a typical corpus, it will tag only about an eighth of the tokens correctly:
|
Default taggers assign their tag to every single word, even words that have never been encountered before. As it happens, most new words are nouns. Thus, default taggers help to improve the robustness of a language processing system. We will return to them later, in the context of our discussion of backoff.
3.2.5 Exercises
- ☼ Working with someone else, take turns to pick a word that can be either a noun or a verb (e.g. contest); the opponent has to predict which one is likely to be the most frequent in the Brown corpus; check the opponent's prediction, and tally the score over several turns.
- ◑ Write programs to process the Brown Corpus and find answers to the following
questions:
- Which nouns are more common in their plural form, rather than their singular form? (Only consider regular plurals, formed with the -s suffix.)
- Which word has the greatest number of distinct tags. What are they, and what do they represent?
- List tags in order of decreasing frequency. What do the 20 most frequent tags represent?
- Which tags are nouns most commonly found after? What do these tags represent?
- ◑ Generate some statistics for tagged data to answer the following questions:
- What proportion of word types are always assigned the same part-of-speech tag?
- How many words are ambiguous, in the sense that they appear with at least two tags?
- What percentage of word occurrences in the Brown Corpus involve these ambiguous words?
- ◑ Above we gave an example of the nltk.tag.accuracy() function. It has two
arguments, a tagger and some tagged text, and it works out how accurately
the tagger performs on this text. For example, if the supplied tagged text
was [('the', 'DT'), ('dog', 'NN')] and the tagger produced the output
[('the', 'NN'), ('dog', 'NN')], then the accuracy score would be 0.5.
Can you figure out how the nltk.tag.accuracy() function works?
- A tagger takes a list of words as input, and produces a list of tagged words as output. However, nltk.tag.accuracy() is given correctly tagged text as its input. What must the nltk.tag.accuracy() function do with this input before performing the tagging?
- Once the supplied tagger has created newly tagged text, how would nltk.tag.accuracy() go about comparing it with the original tagged text and computing the accuracy score?
3.3 Looking for Patterns in Words
3.3.1 Some Morphology
English nouns can be morphologically complex. For example, words like books and women are plural. Words with the -ness suffix are nouns that have been derived from adjectives, e.g. happiness and illness. The -ment suffix appears on certain nouns derived from verbs, e.g. government and establishment.
English verbs can also be morphologically complex. For instance, the present participle of a verb ends in -ing, and expresses the idea of ongoing, incomplete action (e.g. falling, eating). The -ing suffix also appears on nouns derived from verbs, e.g. the falling of the leaves (this is known as the gerund). In the Brown corpus, these are tagged VBG.
The past participle of a verb often ends in -ed, and expresses the idea of a completed action (e.g. walked, cried). These are tagged VBD.
Common tag sets often capture some morpho-syntactic information; that is, information about the kind of morphological markings that words receive by virtue of their syntactic role. Consider, for example, the selection of distinct grammatical forms of the word go illustrated in the following sentences:
| (4) |
|
Each of these forms — go, goes, gone, and went — is morphologically distinct from the others. Consider the form, goes. This cannot occur in all grammatical contexts, but requires, for instance, a third person singular subject. Thus, the following sentences are ungrammatical.
| (5) |
|
By contrast, gone is the past participle form; it is required after have (and cannot be replaced in this context by goes), and cannot occur as the main verb of a clause.
| (6) |
|
We can easily imagine a tag set in which the four distinct grammatical forms just discussed were all tagged as VB. Although this would be adequate for some purposes, a more fine-grained tag set will provide useful information about these forms that can be of value to other processors that try to detect syntactic patterns from tag sequences. As we noted at the beginning of this chapter, the Brown tag set does in fact capture these distinctions, as summarized in Table 3.4.
| Form | Category | Tag |
|---|---|---|
| go | base | VB |
| goes | 3rd singular present | VBZ |
| gone | past participle | VBN |
| going | gerund | VBG |
| went | simple past | VBD |
In addition to this set of verb tags, the various forms of the verb to be have special tags: be/BE, being/BEG, am/BEM, been/BEN and was/BEDZ. All told, this fine-grained tagging of verbs means that an automatic tagger that uses this tag set is in effect carrying out a limited amount of morphological analysis.
Most part-of-speech tag sets make use of the same basic categories, such as noun, verb, adjective, and preposition. However, tag sets differ both in how finely they divide words into categories, and in how they define their categories. For example, is might be tagged simply as a verb in one tag set; but as a distinct form of the lexeme BE in another tag set (as in the Brown Corpus). This variation in tag sets is unavoidable, since part-of-speech tags are used in different ways for different tasks. In other words, there is no one 'right way' to assign tags, only more or less useful ways depending on one's goals. More details about the Brown corpus tag set can be found in the Appendix at the end of this chapter.
3.3.2 The Regular Expression Tagger
The regular expression tagger assigns tags to tokens on the basis of matching patterns. For instance, we might guess that any word ending in ed is the past participle of a verb, and any word ending with 's is a possessive noun. We can express these as a list of regular expressions:
|
Note that these are processed in order, and the first one that matches is applied.
Now we can set up a tagger and use it to tag some text.
|
How well does this do?
|
The regular expression is a catch-all that tags everything as a noun. This is equivalent to the default tagger (only much less efficient). Instead of re-specifying this as part of the regular expression tagger, is there a way to combine this tagger with the default tagger? We will see how to do this later, under the heading of backoff taggers.
3.3.3 Exercises
- ☼ Search the web for "spoof newspaper headlines", to find such gems as: British Left Waffles on Falkland Islands, and Juvenile Court to Try Shooting Defendant. Manually tag these headlines to see if knowledge of the part-of-speech tags removes the ambiguity.
- ☼ Satisfy yourself that there are restrictions on the distribution of go and went, in the sense that they cannot be freely interchanged in the kinds of contexts illustrated in (4d).
- ◑ Write code to search the Brown Corpus for particular words and phrases
according to tags, to answer the following questions:
- Produce an alphabetically sorted list of the distinct words tagged as MD.
- Identify words that can be plural nouns or third person singular verbs (e.g. deals, flies).
- Identify three-word prepositional phrases of the form IN + DET + NN (eg. in the lab).
- What is the ratio of masculine to feminine pronouns?
- ◑ In the introduction we saw a table involving frequency counts for the verbs adore, love, like, prefer and preceding qualifiers such as really. Investigate the full range of qualifiers (Brown tag QL) that appear before these four verbs.
- ◑ We defined the regexp_tagger that can be used as a fall-back tagger for unknown words. This tagger only checks for cardinal numbers. By testing for particular prefix or suffix strings, it should be possible to guess other tags. For example, we could tag any word that ends with -s as a plural noun. Define a regular expression tagger (using nltk.RegexpTagger) that tests for at least five other patterns in the spelling of words. (Use inline documentation to explain the rules.)
- ◑ Consider the regular expression tagger developed in the exercises in the previous section. Evaluate the tagger using nltk.tag.accuracy(), and try to come up with ways to improve its performance. Discuss your findings. How does objective evaluation help in the development process?
- ★ There are 264 distinct words in the Brown Corpus having exactly
three possible tags.
- Print a table with the integers 1..10 in one column, and the number of distinct words in the corpus having 1..10 distinct tags.
- For the word with the greatest number of distinct tags, print out sentences from the corpus containing the word, one for each possible tag.
- ★ Write a program to classify contexts involving the word must according to the tag of the following word. Can this be used to discriminate between the epistemic and deontic uses of must?
3.4 Baselines and Backoff
So far the performance of our simple taggers has been disappointing. Before we embark on a process to get 90+% performance, we need to do two more things. First, we need to establish a more principled baseline performance than the default tagger, which was too simplistic, and the regular expression tagger, which was too arbitrary. Second, we need a way to connect multiple taggers together, so that if a more specialized tagger is unable to assign a tag, we can "back off" to a more generalized tagger.
3.4.1 The Lookup Tagger
A lot of high-frequency words do not have the NN tag. Let's find some of these words and their tags. The following code takes a list of sentences and counts up the words, and prints the 100 most frequent words:
|
Next, let's inspect the tags that these words have. First we will do this in the most obvious (but highly inefficient) way:
|
A much better approach is to set up a dictionary that maps each of the 100 most frequent words to its most likely tag. We can do this by setting up a frequency distribution cfd over the tagged words, i.e. the frequency of the different tags that occur with each word.
|
Now for any word that appears in this section of the corpus, we can determine its most likely tag:
|
Finally, we can create and evaluate a simple tagger that assigns tags to words based on this table:
|
This is surprisingly good; just knowing the tags for the 100 most frequent words enables us to tag nearly half of all words correctly! Let's see what it does on some untagged input text:
|
Notice that a lot of these words have been assigned a tag of None. That is because they were not among the 100 most frequent words. In these cases we would like to assign the default tag of NN, a process known as backoff.
3.4.2 Backoff
How do we combine these taggers? We want to use the lookup table first, and if it is unable to assign a tag, then use the default tagger. We do this by specifying the default tagger as an argument to the lookup tagger. The lookup tagger will call the default tagger just in case it can't assign a tag itself.
|
We will return to this technique in the context of a broader discussion on combining taggers in Section 3.5.6.
3.4.3 Choosing a Good Baseline
We can put all this together to write a simple (but somewhat inefficient) program to create and evaluate lookup taggers having a range of sizes, as shown in Listing 3.3. We include a backoff tagger that tags everything as a noun. A consequence of using this backoff tagger is that the lookup tagger only has to store word/tag pairs for words other than nouns.
| ||
| ||
Listing 3.3 (baseline_tagger.py): Lookup Tagger Performance with Varying Model Size |
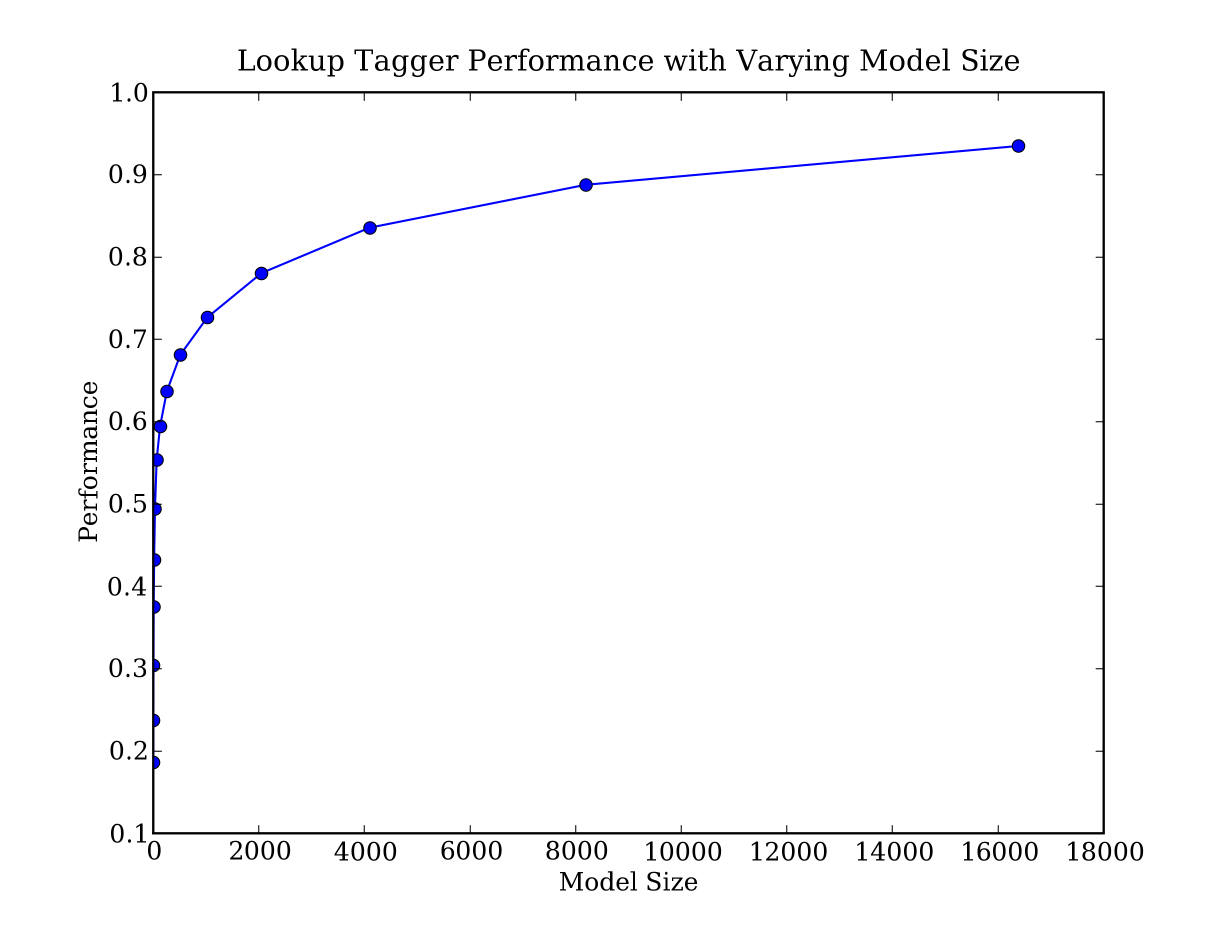
Figure 3.2: Lookup Tagger
Observe that performance initially increases rapidly as the model size grows, eventually reaching a plateau, when large increases in model size yield little improvement in performance. (This example used the pylab plotting package; we will return to this later in Section 5.3.4).
3.4.4 Exercises
- ◑ Explore the following issues that arise in connection with the lookup tagger:
- What happens to the tagger performance for the various model sizes when a backoff tagger is omitted?
- Consider the curve in Figure 3.2; suggest a good size for a lookup tagger that balances memory and performance. Can you come up with scenarios where it would be preferable to minimize memory usage, or to maximize performance with no regard for memory usage?
- ◑ What is the upper limit of performance for a lookup tagger, assuming no limit to the size of its table? (Hint: write a program to work out what percentage of tokens of a word are assigned the most likely tag for that word, on average.)
3.5 Getting Better Coverage
3.5.1 More English Word Classes
Two other important word classes are adjectives and adverbs. Adjectives describe nouns, and can be used as modifiers (e.g. large in the large pizza), or in predicates (e.g. the pizza is large). English adjectives can be morphologically complex (e.g. fallV+ing in the falling stocks). Adverbs modify verbs to specify the time, manner, place or direction of the event described by the verb (e.g. quickly in the stocks fell quickly). Adverbs may also modify adjectives (e.g. really in Mary's teacher was really nice).
English has several categories of closed class words in addition to prepositions, such as articles (also often called determiners) (e.g., the, a), modals (e.g., should, may), and personal pronouns (e.g., she, they). Each dictionary and grammar classifies these words differently.
Part-of-speech tags are closely related to the notion of word class used in syntax. The assumption in linguistics is that every distinct word type will be listed in a lexicon (or dictionary), with information about its pronunciation, syntactic properties and meaning. A key component of the word's properties will be its class. When we carry out a syntactic analysis of an example like fruit flies like a banana, we will look up each word in the lexicon, determine its word class, and then group it into a hierarchy of phrases, as illustrated in the following parse tree.
Syntactic analysis will be dealt with in more detail in Part II. For now, we simply want to make the connection between the labels used in syntactic parse trees and part-of-speech tags. Table 3.5 shows the correspondence:
| Word Class Label | Brown Tag | Word Class |
|---|---|---|
| Det | AT | article |
| N | NN | noun |
| V | VB | verb |
| Adj | JJ | adjective |
| P | IN | preposition |
| Card | CD | cardinal number |
| -- | . | sentence-ending punctuation |
3.5.2 Some Diagnostics
Now that we have examined word classes in detail, we turn to a more basic question: how do we decide what category a word belongs to in the first place? In general, linguists use three criteria: morphological (or formal); syntactic (or distributional); semantic (or notional). A morphological criterion is one that looks at the internal structure of a word. For example, -ness is a suffix that combines with an adjective to produce a noun. Examples are happy → happiness, ill → illness. So if we encounter a word that ends in -ness, this is very likely to be a noun.
A syntactic criterion refers to the contexts in which a word can occur. For example, assume that we have already determined the category of nouns. Then we might say that a syntactic criterion for an adjective in English is that it can occur immediately before a noun, or immediately following the words be or very. According to these tests, near should be categorized as an adjective:
| (7) |
|
A familiar example of a semantic criterion is that a noun is "the name of a person, place or thing". Within modern linguistics, semantic criteria for word classes are treated with suspicion, mainly because they are hard to formalize. Nevertheless, semantic criteria underpin many of our intuitions about word classes, and enable us to make a good guess about the categorization of words in languages that we are unfamiliar with. For example, if we all we know about the Dutch verjaardag is that it means the same as the English word birthday, then we can guess that verjaardag is a noun in Dutch. However, some care is needed: although we might translate zij is vandaag jarig as it's her birthday today, the word jarig is in fact an adjective in Dutch, and has no exact equivalent in English!
All languages acquire new lexical items. A list of words recently added to the Oxford Dictionary of English includes cyberslacker, fatoush, blamestorm, SARS, cantopop, bupkis, noughties, muggle, and robata. Notice that all these new words are nouns, and this is reflected in calling nouns an open class. By contrast, prepositions are regarded as a closed class. That is, there is a limited set of words belonging to the class (e.g., above, along, at, below, beside, between, during, for, from, in, near, on, outside, over, past, through, towards, under, up, with), and membership of the set only changes very gradually over time.
3.5.3 Unigram Tagging
Unigram taggers are based on a simple statistical algorithm:
for each token, assign the tag that is most likely for
that particular token. For example, it will assign the tag JJ to any
occurrence of the word frequent, since frequent is used as an
adjective (e.g. a frequent word) more often than it is used as a
verb (e.g. I frequent this cafe).
A unigram tagger behaves just like a lookup tagger (Section 3.4.1),
except there is a more convenient technique for setting it up,
called training. In the following code sample,
we initialize and train a unigram tagger (line ![[1]](callouts/callout1.gif) ),
use it to tag a sentence, then finally compute the tagger's overall accuracy:
),
use it to tag a sentence, then finally compute the tagger's overall accuracy:
|
3.5.4 Affix Taggers
Affix taggers are like unigram taggers, except they are trained on word prefixes or suffixes of a specified length. (NB. Here we use prefix and suffix in the string sense, not the morphological sense.) For example, the following tagger will consider suffixes of length 3 (e.g. -ize, -ion), for words having at least 5 characters.
|
3.5.5 N-Gram Taggers
When we perform a language processing task based on unigrams, we are using one item of context. In the case of tagging, we only consider the current token, in isolation from any larger context. Given such a model, the best we can do is tag each word with its a priori most likely tag. This means we would tag a word such as wind with the same tag, regardless of whether it appears in the context the wind or to wind.
An n-gram tagger is a generalization of a unigram tagger whose context is the current word together with the part-of-speech tags of the n-1 preceding tokens, as shown in Figure 3.3. The tag to be chosen, tn, is circled, and the context is shaded in grey. In the example of an n-gram tagger shown in Figure 3.3, we have n=3; that is, we consider the tags of the two preceding words in addition to the current word. An n-gram tagger picks the tag that is most likely in the given context.
Figure 3.3: Tagger Context
Note
A 1-gram tagger is another term for a unigram tagger: i.e., the context used to tag a token is just the text of the token itself. 2-gram taggers are also called bigram taggers, and 3-gram taggers are called trigram taggers.
The NgramTagger class uses a tagged training corpus to determine which part-of-speech tag is most likely for each context. Here we see a special case of an n-gram tagger, namely a bigram tagger. First we train it, then use it to tag untagged sentences:
|
As with the other taggers, n-gram taggers assign the tag None to any token whose context was not seen during training.
As n gets larger, the specificity of the contexts increases, as does the chance that the data we wish to tag contains contexts that were not present in the training data. This is known as the sparse data problem, and is quite pervasive in NLP. Thus, there is a trade-off between the accuracy and the coverage of our results (and this is related to the precision/recall trade-off in information retrieval).
Note
n-gram taggers should not consider context that crosses a sentence boundary. Accordingly, NLTK taggers are designed to work with lists of sentences, where each sentence is a list of words. At the start of a sentence, tn-1 and preceding tags are set to None.
3.5.6 Combining Taggers
One way to address the trade-off between accuracy and coverage is to use the more accurate algorithms when we can, but to fall back on algorithms with wider coverage when necessary. For example, we could combine the results of a bigram tagger, a unigram tagger, and a regexp_tagger, as follows:
- Try tagging the token with the bigram tagger.
- If the bigram tagger is unable to find a tag for the token, try the unigram tagger.
- If the unigram tagger is also unable to find a tag, use a default tagger.
Most NLTK taggers permit a backoff-tagger to be specified. The backoff-tagger may itself have a backoff tagger:
|
Note
We specify the backoff tagger when the tagger is initialized, so that training can take advantage of the backoff tagger. Thus, if the bigram tagger would assign the same tag as its unigram backoff tagger in a certain context, the bigram tagger discards the training instance. This keeps the bigram tagger model as small as possible. We can further specify that a tagger needs to see more than one instance of a context in order to retain it, e.g. nltk.BigramTagger(sents, cutoff=2, backoff=t1) will discard contexts that have only been seen once or twice.
3.5.7 Tagging Unknown Words
Our approach to tagging unknown words still uses backoff to a regular-expression tagger or a default tagger. These are unable to make use of context. Thus, if our tagger encountered the word blog, not seen during training, it would assign it a tag regardless of whether this word appeared in the context the blog or to blog. How can we do better with these unknown words, or out-of-vocabulary items?
A useful method to tag unknown words based on context is to limit the vocabulary of a tagger to the most frequent n words, and to replace every other word with a special word UNK. During training, a unigram tagger will probably learn that this "word" is usually a noun. However, the n-gram taggers will detect contexts in which it has some other tag. For example, if the preceding word is to (tagged TO), then UNK will probably be tagged as a verb. Full exploration of this method is left to the exercises.
3.5.8 Storing Taggers
Training a tagger on a large corpus may take several minutes. Instead of training a tagger every time we need one, it is convenient to save a trained tagger in a file for later re-use. Let's save our tagger t2 to a file t2.pkl.
|
Now, in a separate Python process, we can load our saved tagger.
|
Now let's check that it can be used for tagging.
|
3.5.9 Exercises
- ☼ Train a unigram tagger and run it on some new text. Observe that some words are not assigned a tag. Why not?
- ☼ Train an affix tagger AffixTagger() and run it on some new text. Experiment with different settings for the affix length and the minimum word length. Can you find a setting that seems to perform better than the one described above? Discuss your findings.
- ☼ Train a bigram tagger with no backoff tagger, and run it on some of the training data. Next, run it on some new data. What happens to the performance of the tagger? Why?
- ◑ Write a program that calls AffixTagger() repeatedly, using different settings for the affix length and the minimum word length. What parameter values give the best overall performance? Why do you think this is the case?
- ◑ How serious is the sparse data problem? Investigate the performance of n-gram taggers as n increases from 1 to 6. Tabulate the accuracy score. Estimate the training data required for these taggers, assuming a vocabulary size of 105 and a tagset size of 102.
- ◑ Obtain some tagged data for another language, and train and evaluate a variety of taggers on it. If the language is morphologically complex, or if there are any orthographic clues (e.g. capitalization) to word classes, consider developing a regular expression tagger for it (ordered after the unigram tagger, and before the default tagger). How does the accuracy of your tagger(s) compare with the same taggers run on English data? Discuss any issues you encounter in applying these methods to the language.
- ★
Create a default tagger and various unigram and n-gram taggers,
incorporating backoff, and train them on part of the Brown corpus.
- Create three different combinations of the taggers. Test the accuracy of each combined tagger. Which combination works best?
- Try varying the size of the training corpus. How does it affect your results?
- ★
Our approach for tagging an unknown word has been to consider the letters of the word
(using RegexpTagger() and AffixTagger()), or to ignore the word altogether and tag
it as a noun (using nltk.DefaultTagger()). These methods will not do well for texts having
new words that are not nouns.
Consider the sentence I like to blog on Kim's blog. If blog is a new
word, then looking at the previous tag (TO vs NP$) would probably be helpful.
I.e. we need a default tagger that is sensitive to the preceding tag.
- Create a new kind of unigram tagger that looks at the tag of the previous word, and ignores the current word. (The best way to do this is to modify the source code for UnigramTagger(), which presumes knowledge of Python classes discussed in Section 9.)
- Add this tagger to the sequence of backoff taggers (including ordinary trigram and bigram taggers that look at words), right before the usual default tagger.
- Evaluate the contribution of this new unigram tagger.
- ★ Write code to preprocess tagged training data, replacing all but the most frequent n words with the special word UNK. Train an n-gram backoff tagger on this data, then use it to tag some new text. Note that you will have to preprocess the text to replace unknown words with UNK, and post-process the tagged output to replace the UNK words with the words from the original input.
3.6 Summary
- Words can be grouped into classes, such as nouns, verbs, adjectives, and adverbs. These classes are known as lexical categories or parts of speech. Parts of speech are assigned short labels, or tags, such as NN, VB,
- The process of automatically assigning parts of speech to words in text is called part-of-speech tagging, POS tagging, or just tagging.
- Some linguistic corpora, such as the Brown Corpus, have been POS tagged.
- A variety of tagging methods are possible, e.g. default tagger, regular expression tagger, unigram tagger and n-gram taggers. These can be combined using a technique known as backoff.
- Taggers can be trained and evaluated using tagged corpora.
- Part-of-speech tagging is an important, early example of a sequence classification task in NLP: a classification decision at any one point in the sequence makes use of words and tags in the local context.
3.7 Further Reading
For more examples of tagging with NLTK, please see the guide at http://nltk.org/doc/guides/tag.html. Chapters 4 and 5 of [Jurafsky & Martin, 2008] contain more advanced material on n-grams and part-of-speech tagging.
There are several other important approaches to tagging involving Transformation-Based Learning, Markov Modeling, and Finite State Methods. (We will discuss some of these in Chapter 4.) In Chapter 6 we will see a generalization of tagging called chunking in which a contiguous sequence of words is assigned a single tag.
Part-of-speech tagging is just one kind of tagging, one that does not depend on deep linguistic analysis. There are many other kinds of tagging. Words can be tagged with directives to a speech synthesizer, indicating which words should be emphasized. Words can be tagged with sense numbers, indicating which sense of the word was used. Words can also be tagged with morphological features. Examples of each of these kinds of tags are shown below. For space reasons, we only show the tag for a single word. Note also that the first two examples use XML-style tags, where elements in angle brackets enclose the word that is tagged.
- Speech Synthesis Markup Language (W3C SSML): That is a <emphasis>big</emphasis> car!
- SemCor: Brown Corpus tagged with WordNet senses: Space in any <wf pos="NN" lemma="form" wnsn="4">form</wf> is completely measured by the three dimensions. (Wordnet form/nn sense 4: "shape, form, configuration, contour, conformation")
- Morphological tagging, from the Turin University Italian Treebank: E' italiano , come progetto e realizzazione , il primo (PRIMO ADJ ORDIN M SING) porto turistico dell' Albania .
Tagging exhibits several properties that are characteristic of natural language processing. First, tagging involves classification: words have properties; many words share the same property (e.g. cat and dog are both nouns), while some words can have multiple such properties (e.g. wind is a noun and a verb). Second, in tagging, disambiguation occurs via representation: we augment the representation of tokens with part-of-speech tags. Third, training a tagger involves sequence learning from annotated corpora. Finally, tagging uses simple, general, methods such as conditional frequency distributions and transformation-based learning.
Note that tagging is also performed at higher levels. Here is an example of dialogue act tagging, from the NPS Chat Corpus [Forsyth & Martell, 2007], included with NLTK.
List of available taggers: http://www-nlp.stanford.edu/links/statnlp.html
3.8 Appendix: Brown Tag Set
Table 3.6 gives a sample of closed class words, following the classification of the Brown Corpus. (Note that part-of-speech tags may be presented as either upper-case or lower-case strings — the case difference is not significant.)
| AP | determiner/pronoun, post-determiner | many other next more last former little several enough most least only very few fewer past same |
| AT | article | the an no a every th' ever' ye |
| CC | conjunction, coordinating | and or but plus & either neither nor yet 'n' and/or minus an' |
| CS | conjunction, subordinating | that as after whether before while like because if since for than until so unless though providing once lest till whereas whereupon supposing albeit then |
| IN | preposition | of in for by considering to on among at through with under into regarding than since despite ... |
| MD | modal auxiliary | should may might will would must can could shall ought need wilt |
| PN | pronoun, nominal | none something everything one anyone nothing nobody everybody everyone anybody anything someone no-one nothin' |
| PPL | pronoun, singular, reflexive | itself himself myself yourself herself oneself ownself |
| PP$ | determiner, possessive | our its his their my your her out thy mine thine |
| PP$$ | pronoun, possessive | ours mine his hers theirs yours |
| PPS | pronoun, personal, nom, 3rd pers sng | it he she thee |
| PPSS | pronoun, personal, nom, not 3rd pers sng | they we I you ye thou you'uns |
| WDT | WH-determiner | which what whatever whichever |
| WPS | WH-pronoun, nominative | that who whoever whosoever what whatsoever |
3.8.1 Acknowledgments
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
4 Data-Intensive Language Processing
Note
this chapter is currently in preparation
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
Introduction to Part II
Part II covers the linguistic and computational analysis of sentences. We will see that sentences have systematic structure; we use this to communicate who did what to whom. Linguistic structures are formalized using context-free grammars, and processed computationally using parsers. Various extensions are covered, including chart parsers and probabilistic parsers. Part II also introduces the techniques in structured programming needed for implementing grammars and parsers.
5 Structured Programming in Python
5.1 Introduction
In Part I you had an intensive introduction to Python (Chapter 1) followed by chapters on words, tags, and chunks (Chapters 2-6). These chapters contain many examples and exercises that should have helped you consolidate your Python skills and apply them to simple NLP tasks. So far our programs — and the data we have been processing — have been relatively unstructured. In Part II we will focus on structure: i.e. structured programming with structured data.
In this chapter we will review key programming concepts and explain many of the minor points that could easily trip you up. More fundamentally, we will introduce important concepts in structured programming that help you write readable, well-organized programs that you and others will be able to re-use. Each section is independent, so you can easily select what you most need to learn and concentrate on that. As before, this chapter contains many examples and exercises (and as before, some exercises introduce new material). Readers new to programming should work through them carefully and consult other introductions to programming if necessary; experienced programmers can quickly skim this chapter.
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint
5.2 Back to the Basics
Let's begin by revisiting some of the fundamental operations and data structures required for natural language processing in Python. It is important to appreciate several finer points in order to write Python programs that are not only correct but also idiomatic — by this, we mean using the features of the Python language in a natural and concise way. To illustrate, here is a technique for iterating over the members of a list by initializing an index i and then incrementing the index each time we pass through the loop:
|
Although this does the job, it is not idiomatic Python. By contrast, Python's for statement allows us to achieve the same effect much more succinctly:
|
We'll start with the most innocuous operation of all: assignment. Then we will look at sequence types in detail.
5.2.1 Assignment
Python's assignment statement operates on values. But what is a value? Consider the following code fragment:
This code shows that when we write word2 = word1 in line ![[1]](callouts/callout1.gif) ,
the value of word1 (the string 'Monty') is assigned to word2.
That is, word2 is a copy of word1, so when we overwrite
word1 with a new string 'Python' in line
,
the value of word1 (the string 'Monty') is assigned to word2.
That is, word2 is a copy of word1, so when we overwrite
word1 with a new string 'Python' in line ![[2]](callouts/callout2.gif) , the value
of word2 is not affected.
, the value
of word2 is not affected.
However, assignment statements do not always involve making copies in this way.
An important subtlety of Python is that the "value" of a structured object
(such as a list) is actually a reference to the object. In the
following example, line ![[1]](callouts/callout1.gif) assigns the reference of list1 to the new variable list2.
When we modify something inside list1 on line
assigns the reference of list1 to the new variable list2.
When we modify something inside list1 on line ![[2]](callouts/callout2.gif) , we can see
that the contents of list2 have also been changed.
, we can see
that the contents of list2 have also been changed.
|
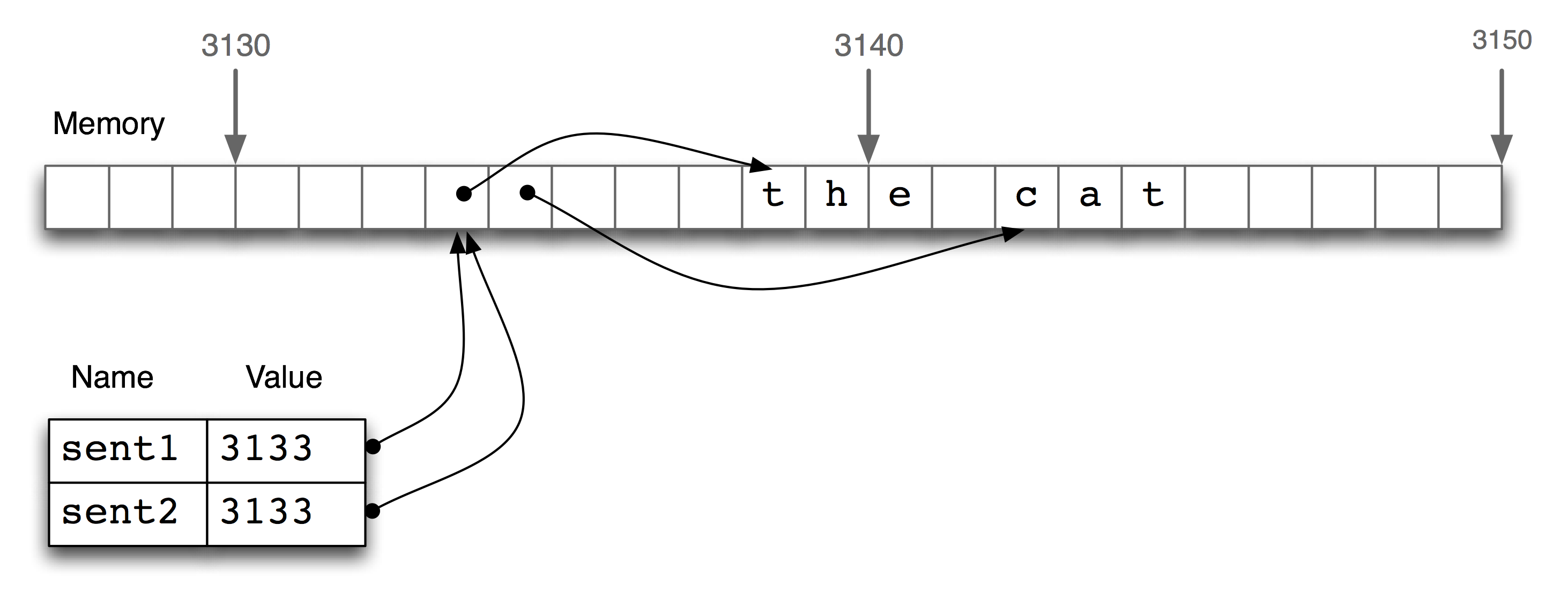
Figure 5.1: List Assignment and Computer Memory
Thus line ![[1]](callouts/callout1.gif) does not copy the contents of the
variable, only its "object reference".
To understand what is going on here, we need to
know how lists are stored in the computer's memory.
In Figure 5.1, we see that a list sent1 is
a reference to an object stored at location 3133 (which is
itself a series of pointers to other locations holding strings).
When we assign sent2 = sent1, it is just the object reference
3133 that gets copied.
does not copy the contents of the
variable, only its "object reference".
To understand what is going on here, we need to
know how lists are stored in the computer's memory.
In Figure 5.1, we see that a list sent1 is
a reference to an object stored at location 3133 (which is
itself a series of pointers to other locations holding strings).
When we assign sent2 = sent1, it is just the object reference
3133 that gets copied.
5.2.2 Sequences: Strings, Lists and Tuples
We have seen three kinds of sequence object: strings, lists, and tuples. As sequences, they have some common properties: they can be indexed and they have a length:
|
We can iterate over the items in a sequence s in a variety of useful ways, as shown in Table 5.1.
| Python Expression | Comment |
|---|---|
| for item in s | iterate over the items of s |
| for item in sorted(s) | iterate over the items of s in order |
| for item in set(s) | iterate over unique elements of s |
| for item in reversed(s) | iterate over elements of s in reverse |
| for item in set(s).difference(t) | iterate over elements of s not in t |
| for item in random.shuffle(s) | iterate over elements of s in random order |
The sequence functions illustrated in Table 5.1 can be combined in various ways; for example, to get unique elements of s sorted in reverse, use reversed(sorted(set(s))).
We can convert between these sequence types. For example, tuple(s) converts any kind of sequence into a tuple, and list(s) converts any kind of sequence into a list. We can convert a list of strings to a single string using the join() function, e.g. ':'.join(words).
Notice in the above code sample that we computed multiple values on a single line, separated by commas. These comma-separated expressions are actually just tuples — Python allows us to omit the parentheses around tuples if there is no ambiguity. When we print a tuple, the parentheses are always displayed. By using tuples in this way, we are implicitly aggregating items together.
In the next example, we use tuples to re-arrange the contents of our list. (We can omit the parentheses because the comma has higher precedence than assignment.)
|
This is an idiomatic and readable way to move items inside a list. It is equivalent to the following traditional way of doing such tasks that does not use tuples (notice that this method needs a temporary variable tmp).
|
As we have seen, Python has sequence functions such as sorted() and reversed() that rearrange the items of a sequence. There are also functions that modify the structure of a sequence and which can be handy for language processing. Thus, zip() takes the items of two sequences and "zips" them together into a single list of pairs. Given a sequence s, enumerate(s) returns an iterator that produces a pair of an index and the item at that index.
|
5.2.3 Combining Different Sequence Types
Let's combine our knowledge of these three sequence types, together with list comprehensions, to perform the task of sorting the words in a string by their length.
|
Each of the above lines of code contains a significant feature.
Line ![[1]](callouts/callout1.gif) demonstrates that a simple string is actually
an object with methods defined on it, such as split().
Line
demonstrates that a simple string is actually
an object with methods defined on it, such as split().
Line ![[2]](callouts/callout2.gif) shows the construction of a list of tuples,
where each tuple consists of a number (the word length) and the
word, e.g. (3, 'the'). Line
shows the construction of a list of tuples,
where each tuple consists of a number (the word length) and the
word, e.g. (3, 'the'). Line ![[3]](callouts/callout3.gif) sorts the list,
modifying the list in-place. Finally, line
sorts the list,
modifying the list in-place. Finally, line ![[4]](callouts/callout4.gif) discards
the length information then joins the words back into a single string.
discards
the length information then joins the words back into a single string.
We began by talking about the commonalities in these sequence types, but the above code illustrates important differences in their roles. First, strings appear at the beginning and the end: this is typical in the context where our program is reading in some text and producing output for us to read. Lists and tuples are used in the middle, but for different purposes. A list is typically a sequence of objects all having the same type, of arbitrary length. We often use lists to hold sequences of words. In contrast, a tuple is typically a collection of objects of different types, of fixed length. We often use a tuple to hold a record, a collection of different fields relating to some entity. This distinction between the use of lists and tuples takes some getting used to, so here is another example:
|
Here, a lexicon is represented as a list because it is a collection of objects of a single type — lexical entries — of no predetermined length. An individual entry is represented as a tuple because it is a collection of objects with different interpretations, such as the orthographic form, the part of speech, and the pronunciations represented in the SAMPA computer readable phonetic alphabet. Note that these pronunciations are stored using a list. (Why?)
The distinction between lists and tuples has been described in terms of usage. However, there is a more fundamental difference: in Python, lists are mutable, while tuples are immutable. In other words, lists can be modified, while tuples cannot. Here are some of the operations on lists that do in-place modification of the list. None of these operations is permitted on a tuple, a fact you should confirm for yourself.
|
5.2.4 Stacks and Queues
Lists are a particularly versatile data type. We can use lists to implement higher-level data types such as stacks and queues. A stack is a container that has a last-in-first-out policy for adding and removing items (see Figure 5.2).
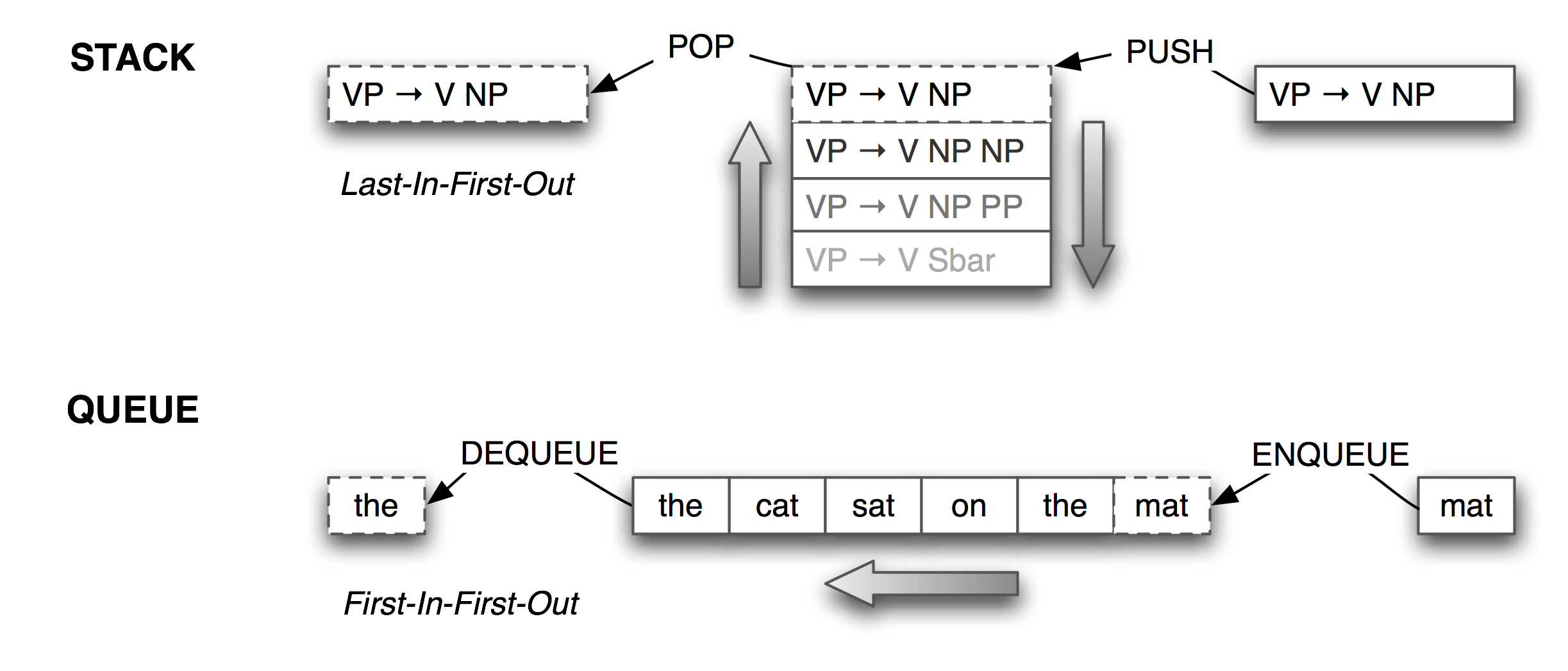
Figure 5.2: Stacks and Queues
Stacks are used to keep track of the current context in computer processing of natural languages (and programming languages too). We will seldom have to deal with stacks explicitly, as the implementation of NLTK parsers, treebank corpus readers, (and even Python functions), all use stacks behind the scenes. However, it is important to understand what stacks are and how they work.
| ||
| ||
Listing 5.1 (check_parens.py): Check parentheses are balanced |
In Python, we can treat a list as a stack by limiting ourselves to the three operations defined on stacks: append(item) (to push item onto the stack), pop() to pop the item off the top of the stack, and [-1] to access the item on the top of the stack. Listing 5.1 processes a sentence with phrase markers, and checks that the parentheses are balanced. The loop pushes material onto the stack when it gets an open parenthesis, and pops the stack when it gets a close parenthesis. We see that two are left on the stack at the end; i.e. the parentheses are not balanced.
Although Listing 5.1 is a useful illustration of stacks, it is overkill because we could have done a direct count: phrase.count('(') == phrase.count(')'). However, we can use stacks for more sophisticated processing of strings containing nested structure, as shown in Listing 5.2. Here we build a (potentially deeply-nested) list of lists. Whenever a token other than a parenthesis is encountered, we add it to a list at the appropriate level of nesting. The stack cleverly keeps track of this level of nesting, exploiting the fact that the item at the top of the stack is actually shared with a more deeply nested item. (Hint: add diagnostic print statements to the function to help you see what it is doing.)
| ||
| ||
Listing 5.2 (convert_parens.py): Convert a nested phrase into a nested list using a stack |
Lists can be used to represent another important data structure. A queue is a container that has a first-in-first-out policy for adding and removing items (see Figure 5.2). Queues are used for scheduling activities or resources. As with stacks, we will seldom have to deal with queues explicitly, as the implementation of NLTK n-gram taggers (Section 3.5.5) and chart parsers (Section 8.2) use queues behind the scenes. However, we will take a brief look at how queues are implemented using lists.
|
5.2.5 More List Comprehensions
You may recall that in Chapter 2, we introduced list comprehensions, with examples like the following:
|
List comprehensions are a convenient and readable way to express list operations in Python, and they have a wide range of uses in natural language processing. In this section we will see some more examples. The first of these takes successive overlapping slices of size n (a sliding window) from a list (pay particular attention to the range of the variable i).
|
You can also use list comprehensions for a kind of multiplication (or cartesian product). Here we generate all combinations of two determiners, two adjectives, and two nouns. The list comprehension is split across three lines for readability.
|
The above example contains three independent for loops. These loops have no variables in common, and we could have put them in any order. We can also have nested loops with shared variables. The next example iterates over all sentences in a section of the Brown Corpus, and for each sentence, iterates over each word.
|
As you will see, the list comprehension in this example contains a final if clause that allows us to filter out any words that fail to meet the specified condition.
Another way to use loop variables is to ignore them! This is
the standard method for building multidimensional structures.
For example, to build an array with m rows and n columns,
where each cell is a set, we would use a nested list comprehension,
as shown in line ![[1]](callouts/callout1.gif) below. Observe that the loop variables
i and j are not used anywhere in the expressions preceding the
for clauses.
below. Observe that the loop variables
i and j are not used anywhere in the expressions preceding the
for clauses.
|
Sometimes we use a list comprehension as part of a larger aggregation task. In the following example we calculate the average length of words in part of the Brown Corpus. Notice that we don't bother storing the list comprehension in a temporary variable, but use it directly as an argument to the average() function.
|
Now that we have reviewed the sequence types, we have one more fundamental data type to revisit.
5.2.6 Dictionaries
As you have already seen, the dictionary data type can be used in a variety of language processing tasks (e.g. Section 1.7). However, we have only scratched the surface. Dictionaries have many more applications than you might have imagined.
Note
The dictionary data type is often known by the name associative array. A normal array maps from integers (the keys) to arbitrary data types (the values), while an associative array places no such constraint on keys. Keys can be strings, tuples, or other more deeply nested structure. Python places the constraint that keys must be immutable.
Let's begin by comparing dictionaries with tuples. Tuples allow access by position; to access the part-of-speech of the following lexical entry we just have to know it is found at index position 1. However, dictionaries allow access by name:
|
In this case, dictionaries are little more than a convenience. We can even simulate access by name using well-chosen constants, e.g.:
|
This method works when there is a closed set of keys and the keys are known in advance. Dictionaries come into their own when we are mapping from an open set of keys, which happens when the keys are drawn from an unrestricted vocabulary or where they are generated by some procedure. Listing 5.3 illustrates the first of these. The function mystery() begins by initializing a dictionary called groups, then populates it with words. We leave it as an exercise for the reader to work out what this function computes. For now, it's enough to note that the keys of this dictionary are an open set, and it would not be feasible to use a integer keys, as would be required if we used lists or tuples for the representation.
| ||
| ||
Listing 5.3 (mystery.py): Mystery program |
Listing 5.3 illustrates two important idioms, which we already
touched on in Chapter 1. First, dictionary keys
are unique; in order to store multiple items in a single entry we
define the value to be a list or a set, and simply update the value each
time we want to store another item (line ![[3]](callouts/callout3.gif) ). Second, if a key does
not yet exist in a dictionary (line
). Second, if a key does
not yet exist in a dictionary (line ![[1]](callouts/callout1.gif) ) we must explicitly add it
and give it an initial value (line
) we must explicitly add it
and give it an initial value (line ![[2]](callouts/callout2.gif) ).
).
The second important use of dictionaries is for mappings that involve compound keys. Suppose we want to categorize a series of linguistic observations according to two or more properties. We can combine the properties using a tuple and build up a dictionary in the usual way, as exemplified in Listing 5.4.
| ||
Listing 5.4 (compound_keys.py): Illustration of compound keys |
5.2.7 Exercises
☼ Find out more about sequence objects using Python's help facility. In the interpreter, type help(str), help(list), and help(tuple). This will give you a full list of the functions supported by each type. Some functions have special names flanked with underscore; as the help documentation shows, each such function corresponds to something more familiar. For example x.__getitem__(y) is just a long-winded way of saying x[y].
☼ Identify three operations that can be performed on both tuples and lists. Identify three list operations that cannot be performed on tuples. Name a context where using a list instead of a tuple generates a Python error.
☼ Find out how to create a tuple consisting of a single item. There are at least two ways to do this.
☼ Create a list words = ['is', 'NLP', 'fun', '?']. Use a series of assignment statements (e.g. words[1] = words[2]) and a temporary variable tmp to transform this list into the list ['NLP', 'is', 'fun', '!']. Now do the same transformation using tuple assignment.
☼ Does the method for creating a sliding window of n-grams behave correctly for the two limiting cases: n = 1, and n = len(sent)?
◑ Create a list of words and store it in a variable sent1. Now assign sent2 = sent1. Modify one of the items in sent1 and verify that sent2 has changed.
- Now try the same exercise but instead assign sent2 = sent1[:]. Modify sent1 again and see what happens to sent2. Explain.
- Now define text1 to be a list of lists of strings (e.g. to represent a text consisting of multiple sentences. Now assign text2 = text1[:], assign a new value to one of the words, e.g. text1[1][1] = 'Monty'. Check what this did to text2. Explain.
- Load Python's deepcopy() function (i.e. from copy import deepcopy), consult its documentation, and test that it makes a fresh copy of any object.
◑ Write code that starts with a string of words and results in a new string consisting of the same words, but where the first word swaps places with the second, and so on. For example, 'the cat sat on the mat' will be converted into 'cat the on sat mat the'.
◑ Initialize an n-by-m list of lists of empty strings using list multiplication, e.g. word_table = [[''] * n] * m. What happens when you set one of its values, e.g. word_table[1][2] = "hello"? Explain why this happens. Now write an expression using range() to construct a list of lists, and show that it does not have this problem.
◑ Write code to initialize a two-dimensional array of sets called word_vowels and process a list of words, adding each word to word_vowels[l][v] where l is the length of the word and v is the number of vowels it contains.
◑ Write code that builds a dictionary of dictionaries of sets.
◑ Use sorted() and set() to get a sorted list of tags used in the Brown corpus, removing duplicates.
◑ Read up on Gematria, a method for assigning numbers to words, and for mapping between words having the same number to discover the hidden meaning of texts (http://en.wikipedia.org/wiki/Gematria, http://essenes.net/gemcal.htm).
Write a function gematria() that sums the numerical values of the letters of a word, according to the letter values in letter_vals:
- letter_vals = {'a':1, 'b':2, 'c':3, 'd':4, 'e':5, 'f':80, 'g':3, 'h':8,
'i':10, 'j':10, 'k':20, 'l':30, 'm':40, 'n':50, 'o':70, 'p':80, 'q':100, 'r':200, 's':300, 't':400, 'u':6, 'v':6, 'w':800, 'x':60, 'y':10, 'z':7}
Use the method from Listing 5.3 to index English words according to their values.
Process a corpus (e.g. nltk.corpus.state_union) and for each document, count how many of its words have the number 666.
Write a function decode() to process a text, randomly replacing words with their Gematria equivalents, in order to discover the "hidden meaning" of the text.
★ Extend the example in Listing 5.4 in the following ways:
- Define two sets verbs and preps, and add each verb and preposition as they are encountered. (Note that you can add an item to a set without bothering to check whether it is already present.)
- Create nested loops to display the results, iterating over verbs and prepositions in sorted order. Generate one line of output per verb, listing prepositions and attachment ratios as follows: raised: about 0:3, at 1:0, by 9:0, for 3:6, from 5:0, in 5:5...
- We used a tuple to represent a compound key consisting of two strings. However, we could have simply concatenated the strings, e.g. key = verb + ":" + prep, resulting in a simple string key. Why is it better to use tuples for compound keys?
5.3 Presenting Results
Often we write a program to report a single datum, such as a particular element in a corpus that meets some complicated criterion, or a single summary statistic such as a word-count or the performance of a tagger. More often, we write a program to produce a structured result, such as a tabulation of numbers or linguistic forms, or a reformatting of the original data. When the results to be presented are linguistic, textual output is usually the most natural choice. However, when the results are numerical, it may be preferable to produce graphical output. In this section you will learn about a variety of ways to present program output.
5.3.1 Strings and Formats
We have seen that there are two ways to display the contents of an object:
|
The print command yields Python's attempt to produce the most human-readable form of an object. The second method — naming the variable at a prompt — shows us a string that can be used to recreate this object. It is important to keep in mind that both of these are just strings, displayed for the benefit of you, the user. They do not give us any clue as to the actual internal representation of the object.
There are many other useful ways to display an object as a string of characters. This may be for the benefit of a human reader, or because we want to export our data to a particular file format for use in an external program.
Formatted output typically contains a combination of variables and pre-specified strings, e.g. given a dictionary wordcount consisting of words and their frequencies we could do:
|
Apart from the problem of unwanted whitespace, print statements that contain alternating variables and constants can be difficult to read and maintain. A better solution is to use formatting strings:
|
5.3.2 Lining Things Up
So far our formatting strings have contained specifications of fixed width, such as %6s, a string that is padded to width 6 and right-justified. We can include a minus sign to make it left-justified. In case we don't know in advance how wide a displayed value should be, the width value can be replaced with a star in the formatting string, then specified using a variable:
|
Other control characters are used for decimal integers and floating point numbers. Since the percent character % has a special interpretation in formatting strings, we have to precede it with another % to get it in the output:
|
An important use of formatting strings is for tabulating data.
The program in Listing 5.5 iterates over five genres of the Brown Corpus.
For each token having the md tag we increment a count. To do this we
have used ConditionalFreqDist(), where the condition is the current genre
and the event is the modal, i.e. this constructs a frequency distribution of
the modal verbs in each genre.
Line ![[1]](callouts/callout1.gif) identifies a small set of modals of interest, and calls
the function tabulate() that
processes the data structure to output the required counts.
Note that we have been careful to separate the language processing
from the tabulation of results.
identifies a small set of modals of interest, and calls
the function tabulate() that
processes the data structure to output the required counts.
Note that we have been careful to separate the language processing
from the tabulation of results.
| ||
| ||
Listing 5.5 (modal_tabulate.py): Frequency of Modals in Different Sections of the Brown Corpus |
There are some interesting patterns in the table produced by Listing 5.5. For instance, compare row d (government literature) with row n (adventure literature); the former is dominated by the use of can, may, must, will while the latter is characterized by the use of could and might. With some further work it might be possible to guess the genre of a new text automatically, simply using information about the distribution of modal verbs.
Our next example, in Listing 5.6, generates a concordance display. We use the left/right justification of strings and the variable width to get vertical alignment of a variable-width window.
[TODO: explain ValueError exception]
| ||
| ||
Listing 5.6 (concordance.py): Simple Concordance Display |
5.3.3 Writing Results to a File
We have seen how to read text from files (Section 2.2.1). It is often useful to write output to files as well. The following code opens a file output.txt for writing, and saves the program output to the file.
|
When we write non-text data to a file we must convert it to a string first. We can do this conversion using formatting strings, as we saw above. We can also do it using Python's backquote notation, which converts any object into a string. Let's write the total number of words to our file, before closing it.
|
5.3.4 Graphical Presentation
So far we have focused on textual presentation and the use of formatted print statements to get output lined up in columns. It is often very useful to display numerical data in graphical form, since this often makes it easier to detect patterns. For example, in Listing 5.5 we saw a table of numbers showing the frequency of particular modal verbs in the Brown Corpus, classified by genre. In Listing 5.7 we present the same information in graphical format. The output is shown in Figure 5.3 (a color figure in the online version).
Note
Listing 5.7 uses the PyLab package which supports sophisticated plotting functions with a MATLAB-style interface. For more information about this package please see http://matplotlib.sourceforge.net/.
| ||
| ||
Listing 5.7 (modal_plot.py): Frequency of Modals in Different Sections of the Brown Corpus |
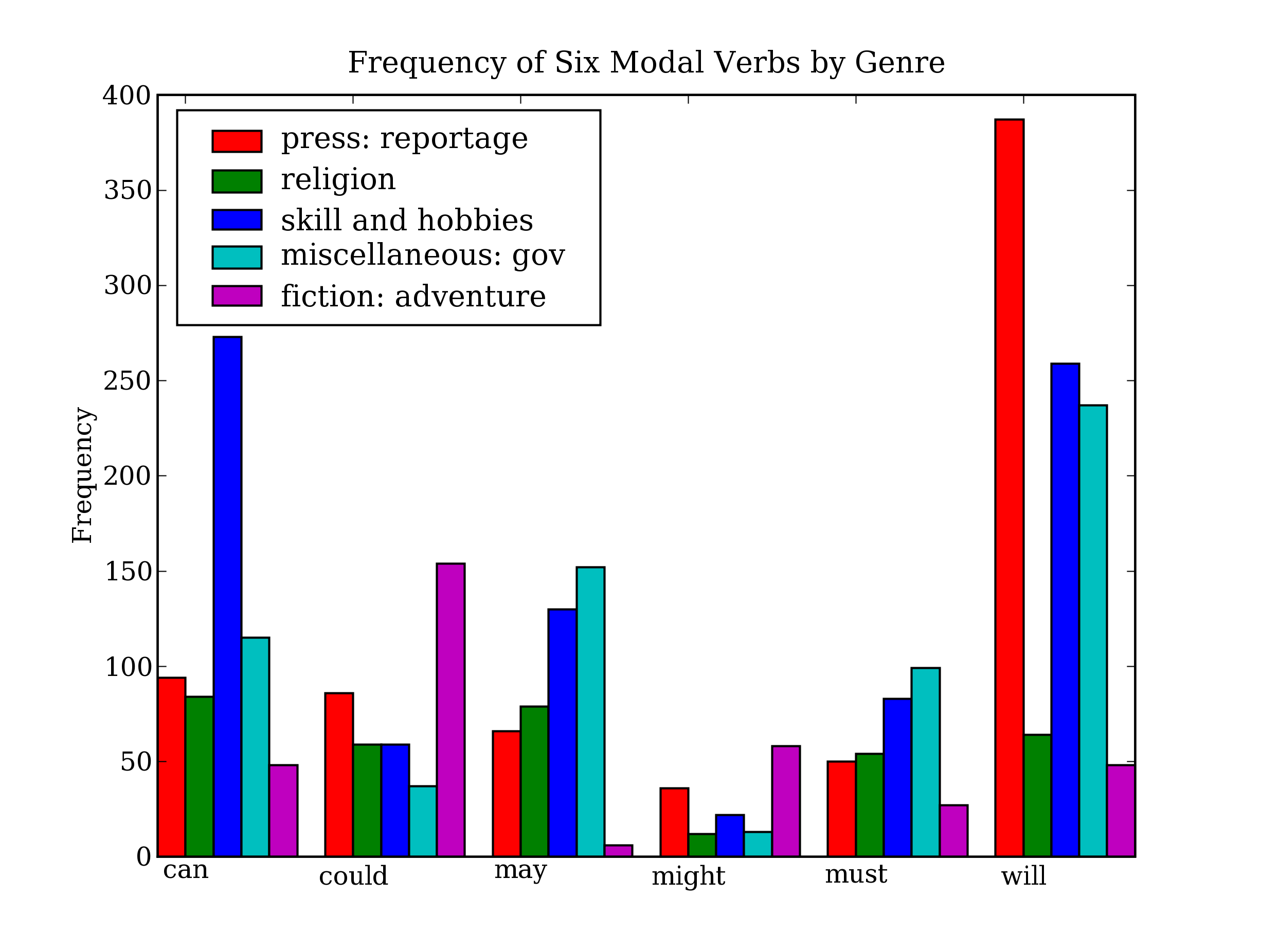
Figure 5.3: Bar Chart Showing Frequency of Modals in Different Sections of Brown Corpus
From the bar chart it is immediately obvious that may and must have almost identical relative frequencies. The same goes for could and might.
5.3.5 Exercises
- ☼ Write code that removes whitespace at the beginning and end of a
string, and normalizes whitespace between words to be a single
space character.
- do this task using split() and join()
- do this task using regular expression substitutions
- ☼ What happens when the formatting strings %6s and %-6s are used to display strings that are longer than six characters?
- ☼ We can use a dictionary to specify the values to be substituted into a formatting string. Read Python's library documentation for formatting strings (http://docs.python.org/lib/typesseq-strings.html), and use this method to display today's date in two different formats.
- ◑ Listing 3.3 in Chapter 3 plotted a curve showing change in the performance of a lookup tagger as the model size was increased. Plot the performance curve for a unigram tagger, as the amount of training data is varied.
5.4 Functions
Once you have been programming for a while, you will find that you need to perform a task that you have done in the past. In fact, over time, the number of completely novel things you have to do in creating a program decreases significantly. Half of the work may involve simple tasks that you have done before. Thus it is important for your code to be re-usable. One effective way to do this is to abstract commonly used sequences of steps into a function, as we briefly saw in Chapter 1.
For example, suppose we find that we often want to read text from an HTML file. This involves several steps: opening the file, reading it in, normalizing whitespace, and stripping HTML markup. We can collect these steps into a function, and give it a name such as get_text():
| ||
Listing 5.8 (get_text.py): Read text from a file |
Now, any time we want to get cleaned-up text from an HTML file, we can just call get_text() with the name of the file as its only argument. It will return a string, and we can assign this to a variable, e.g.: contents = get_text("test.html"). Each time we want to use this series of steps we only have to call the function.
Notice that a function definition consists of the keyword def (short for "define"), followed by the function name, followed by a sequence of parameters enclosed in parentheses, then a colon. The following lines contain an indented block of code, the function body.
Using functions has the benefit of saving space in our program. More importantly, our choice of name for the function helps make the program readable. In the case of the above example, whenever our program needs to read cleaned-up text from a file we don't have to clutter the program with four lines of code, we simply need to call get_text(). This naming helps to provide some "semantic interpretation" — it helps a reader of our program to see what the program "means".
Notice that the above function definition contains a string. The first string inside a function definition is called a docstring. Not only does it document the purpose of the function to someone reading the code, it is accessible to a programmer who has loaded the code from a file:
- get_text(file)
- Read text from a file, normalizing whitespace and stripping HTML markup.
We have seen that functions help to make our work reusable and readable. They also help make it reliable. When we re-use code that has already been developed and tested, we can be more confident that it handles a variety of cases correctly. We also remove the risk that we forget some important step, or introduce a bug. The program that calls our function also has increased reliability. The author of that program is dealing with a shorter program, and its components behave transparently.
- [More: overview of section]
5.4.1 Function Arguments
- multiple arguments
- named arguments
- default values
Python is a dynamically typed language. It does not force us to declare the type of a variable when we write a program. This feature is often useful, as it permits us to define functions that are flexible about the type of their arguments. For example, a tagger might expect a sequence of words, but it wouldn't care whether this sequence is expressed as a list, a tuple, or an iterator.
However, often we want to write programs for later use by others, and want to program in a defensive style, providing useful warnings when functions have not been invoked correctly. Observe that the tag() function in Listing 5.9 behaves sensibly for string arguments, but that it does not complain when it is passed a dictionary.
| ||
| ||
Listing 5.9 (tag1.py): A tagger that tags anything |
It would be helpful if the author of this function took some extra steps to ensure that the word parameter of the tag() function is a string. A naive approach would be to check the type of the argument and return a diagnostic value, such as Python's special empty value, None, as shown in Listing 5.10.
| ||
Listing 5.10 (tag2.py): A tagger that only tags strings |
However, this approach is dangerous because the calling program may not detect the error, and the diagnostic return value may be propagated to later parts of the program with unpredictable consequences. A better solution is shown in Listing 5.11.
| ||
Listing 5.11 (tag3.py): A tagger that generates an error message when not passed a string |
This produces an error that cannot be ignored, since it halts program execution. Additionally, the error message is easy to interpret. (We will see an even better approach, known as "duck typing" in Chapter 9.)
Another aspect of defensive programming concerns the return statement of a function. In order to be confident that all execution paths through a function lead to a return statement, it is best to have a single return statement at the end of the function definition. This approach has a further benefit: it makes it more likely that the function will only return a single type. Thus, the following version of our tag() function is safer:
|
A return statement can be used to pass multiple values back to the calling program, by packing them into a tuple. Here we define a function that returns a tuple consisting of the average word length of a sentence, and the inventory of letters used in the sentence. It would have been clearer to write two separate functions.
|
Functions do not need to have a return statement at all. Some functions do their work as a side effect, printing a result, modifying a file, or updating the contents of a parameter to the function. Consider the following three sort functions; the last approach is dangerous because a programmer could use it without realizing that it had modified its input.
|
5.4.2 An Important Subtlety
Back in Section 5.2.1 you saw that in Python, assignment works on values, but that the value of a structured object is a reference to that object. The same is true for functions. Python interprets function parameters as values (this is known as call-by-value). Consider Listing 5.12. Function set_up() has two parameters, both of which are modified inside the function. We begin by assigning an empty string to w and an empty dictionary to p. After calling the function, w is unchanged, while p is changed:
| ||
| ||
To understand why w was not changed, it is necessary to understand call-by-value. When we called set_up(w, p), the value of w (an empty string) was assigned to a new variable word. Inside the function, the value of word was modified. However, that had no effect on the external value of w. This parameter passing is identical to the following sequence of assignments:
|
In the case of the structured object, matters are quite different. When we called set_up(w, p), the value of p (an empty dictionary) was assigned to a new local variable properties. Since the value of p is an object reference, both variables now reference the same memory location. Modifying something inside properties will also change p, just as if we had done the following sequence of assignments:
|
Thus, to understand Python's call-by-value parameter passing, it is enough to understand Python's assignment operation. We will address some closely related issues in our later discussion of variable scope (Section 9).
5.4.3 Functional Decomposition
Well-structured programs usually make extensive use of functions. When a block of program code grows longer than 10-20 lines, it is a great help to readability if the code is broken up into one or more functions, each one having a clear purpose. This is analogous to the way a good essay is divided into paragraphs, each expressing one main idea.
Functions provide an important kind of abstraction. They allow us to group multiple actions into a single, complex action, and associate a name with it. (Compare this with the way we combine the actions of go and bring back into a single more complex action fetch.) When we use functions, the main program can be written at a higher level of abstraction, making its structure transparent, e.g.
|
Appropriate use of functions makes programs more readable and maintainable. Additionally, it becomes possible to reimplement a function — replacing the function's body with more efficient code — without having to be concerned with the rest of the program.
Consider the freq_words function in Listing 5.13. It updates the contents of a frequency distribution that is passed in as a parameter, and it also prints a list of the n most frequent words.
| ||
| ||
This function has a number of problems. The function has two side-effects: it modifies the contents of its second parameter, and it prints a selection of the results it has computed. The function would be easier to understand and to reuse elsewhere if we initialize the FreqDist() object inside the function (in the same place it is populated), and if we moved the selection and display of results to the calling program. In Listing 5.14 we refactor this function, and simplify its interface by providing a single url parameter.
| ||
| ||
Note that we have now simplified the work of freq_words to the point that we can do its work with three lines of code:
|
5.4.4 Documentation (notes)
- some guidelines for literate programming (e.g. variable and function naming)
- documenting functions (user-level and developer-level documentation)
5.4.5 Functions as Arguments
So far the arguments we have passed into functions have been simple objects like strings, or structured objects like lists. These arguments allow us to parameterize the behavior of a function. As a result, functions are very flexible and powerful abstractions, permitting us to repeatedly apply the same operation on different data. Python also lets us pass a function as an argument to another function. Now we can abstract out the operation, and apply a different operation on the same data. As the following examples show, we can pass the built-in function len() or a user-defined function last_letter() as parameters to another function:
|
Surprisingly, len and last_letter are objects that can be passed around like lists and dictionaries. Notice that parentheses are only used after a function name if we are invoking the function; when we are simply passing the function around as an object these are not used.
Python provides us with one more way to define functions as arguments to other functions, so-called lambda expressions. Supposing there was no need to use the above last_letter() function in multiple places, and thus no need to give it a name. We can equivalently write the following:
|
Our next example illustrates passing a function to the sorted() function. When we call the latter with a single argument (the list to be sorted), it uses the built-in lexicographic comparison function cmp(). However, we can supply our own sort function, e.g. to sort by decreasing length.
|
In 5.2.5 we saw an example of filtering out some items in a list comprehension, using an if test. Similarly, we can restrict a list to just the lexical words, using [word for word in sent if is_lexical(word)]. This is a little cumbersome as it mentions the word variable three times. A more compact way to express the same thing is as follows.
|
The function is_lexical(word) returns True just in case word, when normalized to lowercase, is not in the given list. This function is itself used as an argument to filter(). The filter() function applies its first argument (a function) to each item of its second (a sequence), only passing it through if the function returns true for that item. Thus filter(f, seq) is equivalent to [item for item in seq if apply(f,item) == True].
Another helpful function, which like filter() applies a function to a sequence, is map(). Here is a simple way to find the average length of a sentence in a section of the Brown Corpus:
|
Instead of len(), we could have passed in any other function we liked:
|
Instead of using filter() to call a named function is_vowel, we can define a lambda expression as follows:
|
5.4.6 Exercises
- ☼ Review the answers that you gave for the exercises in 5.2, and rewrite the code as one or more functions.
- ◑ In this section we saw examples of some special functions such as filter() and map(). Other functions in this family are zip() and reduce(). Find out what these do, and write some code to try them out. What uses might they have in language processing?
- ◑ Write a function that takes a list of words (containing duplicates) and returns a list of words (with no duplicates) sorted by decreasing frequency. E.g. if the input list contained 10 instances of the word table and 9 instances of the word chair, then table would appear before chair in the output list.
- ◑ Write a function that takes a text and a vocabulary as its arguments and returns the set of words that appear in the text but not in the vocabulary. Both arguments can be represented as lists of strings. Can you do this in a single line, using set.difference()?
- ◑ As you saw, zip() combines two lists into a single list of pairs. What happens when the lists are of unequal lengths? Define a function myzip() that does something different with unequal lists.
- ◑ Import the itemgetter() function from the operator module in Python's standard library (i.e. from operator import itemgetter). Create a list words containing several words. Now try calling: sorted(words, key=itemgetter(1)), and sorted(words, key=itemgetter(-1)). Explain what itemgetter() is doing.
5.5 Algorithm Design Strategies
A major part of algorithmic problem solving is selecting or adapting an appropriate algorithm for the problem at hand. Whole books are written on this topic (e.g. [Levitin, 2004]) and we only have space to introduce some key concepts and elaborate on the approaches that are most prevalent in natural language processing.
The best known strategy is known as divide-and-conquer. We attack a problem of size n by dividing it into two problems of size n/2, solve these problems, and combine their results into a solution of the original problem. Figure 5.4 illustrates this approach for sorting a list of words.
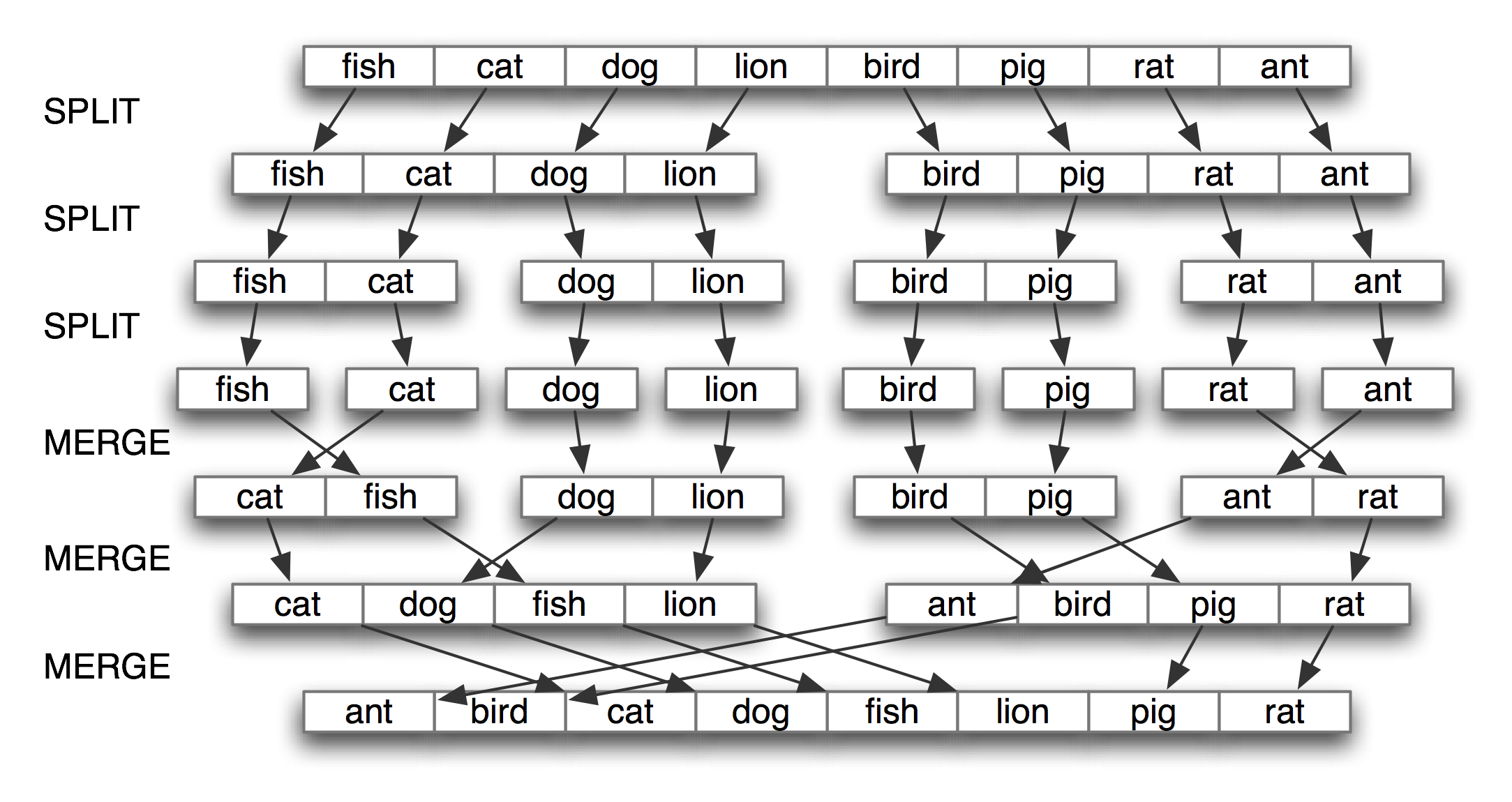
Figure 5.4: Sorting by Divide-and-Conquer (Mergesort)
Another strategy is decrease-and-conquer. In this approach, a small amount of work on a problem of size n permits us to reduce it to a problem of size n/2. Figure 5.5 illustrates this approach for the problem of finding the index of an item in a sorted list.
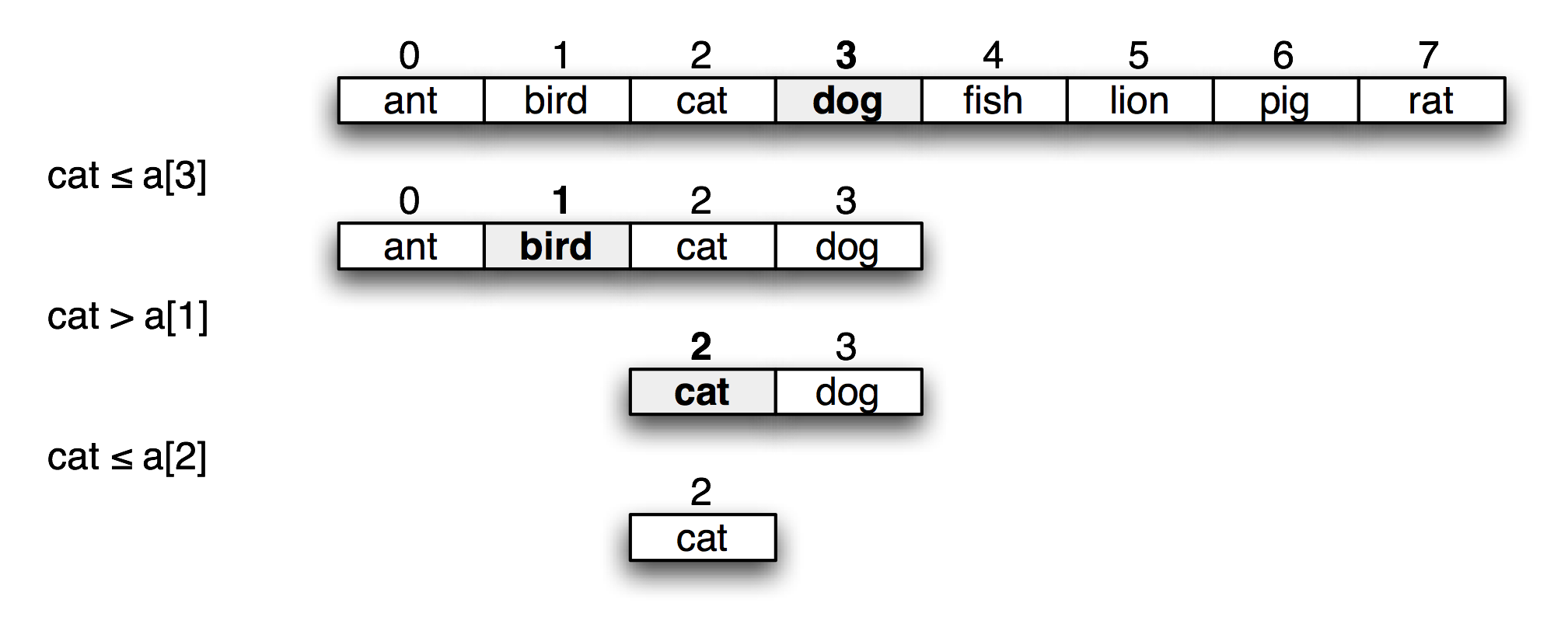
Figure 5.5: Searching by Decrease-and-Conquer (Binary Search)
A third well-known strategy is transform-and-conquer. We attack a problem by transforming it into an instance of a problem we already know how to solve. For example, in order to detect duplicates entries in a list, we can pre-sort the list, then look for adjacent identical items, as shown in Listing 5.15. Our approach to n-gram chunking in Section 6.5 is another case of transform and conquer (why?).
| ||
| ||
Listing 5.15 (presorting.py): Presorting a list for duplicate detection |
5.5.1 Recursion (notes)
We first saw recursion in Chapter 2, in a function that navigated the hypernym hierarchy of WordNet...
Iterative solution:
|
Recursive solution (base case, induction step)
|
[Simple example of recursion on strings.]
Generating all permutations of words, to check which ones are grammatical:
|
5.5.2 Deeply Nested Objects (notes)
We can use recursive functions to build deeply-nested objects. Building a letter trie, Listing 5.16.
| ||
| ||
Listing 5.16 (trie.py): Building a Letter Trie |
5.5.3 Dynamic Programming
Dynamic programming is a general technique for designing algorithms which is widely used in natural language processing. The term 'programming' is used in a different sense to what you might expect, to mean planning or scheduling. Dynamic programming is used when a problem contains overlapping sub-problems. Instead of computing solutions to these sub-problems repeatedly, we simply store them in a lookup table. In the remainder of this section we will introduce dynamic programming, but in a rather different context to syntactic parsing.
Pingala was an Indian author who lived around the 5th century B.C., and wrote a treatise on Sanskrit prosody called the Chandas Shastra. Virahanka extended this work around the 6th century A.D., studying the number of ways of combining short and long syllables to create a meter of length n. He found, for example, that there are five ways to construct a meter of length 4: V4 = {LL, SSL, SLS, LSS, SSSS}. Observe that we can split V4 into two subsets, those starting with L and those starting with S, as shown in (8).
| (8) |
V4 =
LL, LSS
i.e. L prefixed to each item of V2 = {L, SS}
SSL, SLS, SSSS
i.e. S prefixed to each item of V3 = {SL, LS, SSS}
|
| ||
| ||
Listing 5.17 (virahanka.py): Three Ways to Compute Sanskrit Meter |
With this observation, we can write a little recursive function called virahanka1() to compute these meters, shown in Listing 5.17. Notice that, in order to compute V4 we first compute V3 and V2. But to compute V3, we need to first compute V2 and V1. This call structure is depicted in (9).
| (9) |  |
As you can see, V2 is computed twice. This might not seem like a significant problem, but it turns out to be rather wasteful as n gets large: to compute V20 using this recursive technique, we would compute V2 4,181 times; and for V40 we would compute V2 63,245,986 times! A much better alternative is to store the value of V2 in a table and look it up whenever we need it. The same goes for other values, such as V3 and so on. Function virahanka2() implements a dynamic programming approach to the problem. It works by filling up a table (called lookup) with solutions to all smaller instances of the problem, stopping as soon as we reach the value we're interested in. At this point we read off the value and return it. Crucially, each sub-problem is only ever solved once.
Notice that the approach taken in virahanka2() is to solve smaller problems on the way to solving larger problems. Accordingly, this is known as the bottom-up approach to dynamic programming. Unfortunately it turns out to be quite wasteful for some applications, since it may compute solutions to sub-problems that are never required for solving the main problem. This wasted computation can be avoided using the top-down approach to dynamic programming, which is illustrated in the function virahanka3() in Listing 5.17. Unlike the bottom-up approach, this approach is recursive. It avoids the huge wastage of virahanka1() by checking whether it has previously stored the result. If not, it computes the result recursively and stores it in the table. The last step is to return the stored result. The final method is to use a Python decorator called memoize, which takes care of the housekeeping work done by virahanka3() without cluttering up the program.
This concludes our brief introduction to dynamic programming. We will encounter it again in Chapter 8.
5.5.4 Timing (notes)
We can easily test the efficiency gains made by the use of dynamic programming, or any other putative performance enhancement, using the timeit module:
|
[MORE]
5.5.5 Exercises
◑ Write a recursive function lookup(trie, key) that looks up a key in a trie, and returns the value it finds. Extend the function to return a word when it is uniquely determined by its prefix (e.g. vanguard is the only word that starts with vang-, so lookup(trie, 'vang') should return the same thing as lookup(trie, 'vanguard')).
◑ Read about string edit distance and the Levenshtein Algorithm. Try the implementation provided in nltk.edit_dist(). How is this using dynamic programming? Does it use the bottom-up or top-down approach? [See also http://norvig.com/spell-correct.html]
◑ The Catalan numbers arise in many applications of combinatorial mathematics, including the counting of parse trees (Chapter 8). The series can be defined as follows: C0 = 1, and Cn+1 = Σ0..n (CiCn-i).
- Write a recursive function to compute nth Catalan number Cn
- Now write another function that does this computation using dynamic programming
- Use the timeit module to compare the performance of these functions as n increases.
★ Write a recursive function that pretty prints a trie in alphabetically sorted order, as follows
chat: 'cat' --ien: 'dog' -???: ???
★ Write a recursive function that processes text, locating the uniqueness point in each word, and discarding the remainder of each word. How much compression does this give? How readable is the resulting text?
5.6 Conclusion
[TO DO]
5.7 Further Reading
http://docs.python.org/lib/typesseq-strings.html
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
6 Partial Parsing and Interpretation
6.1 Introduction
In processing natural language, we are looking for structure and meaning. Two of the most common methods are segmentation and labeling. Recall that in tokenization, we segment a sequence of characters into tokens, while in tagging we label each of these tokens. Moreover, these two operations of segmentation and labeling go hand in hand. We break up a stream of characters into linguistically meaningful segments (e.g., words) so that we can classify those segments with their part-of-speech categories. The result of such classification is represented by adding a label (e.g., part-of-speech tag) to the segment in question.
We will see that many tasks can be construed as a combination of segmentation and labeling. However, this involves generalizing our notion of segmentation to encompass sequences of tokens. Suppose that we are trying to recognize the names of people, locations and organizations in a piece of text (a task that is usually called Named Entity Recognition). Many of these names will involve more than one token: Cecil H. Green, Escondido Village, Stanford University; indeed, some names may have sub-parts that are also names: Cecil H. Green Library, Escondido Village Conference Service Center. In Named Entity Recognition, therefore, we need to be able to identify the beginning and end of multi-token sequences.
Identifying the boundaries of specific types of word sequences is also required when we want to recognize pieces of syntactic structure. Suppose for example that as a preliminary to Named Entity Recognition, we have decided that it would be useful to just pick out noun phrases from a piece of text. To carry this out in a complete way, we would probably want to use a proper syntactic parser. But parsing can be quite challenging and computationally expensive — is there an easier alternative? The answer is Yes: we can look for sequences of part-of-speech tags in a tagged text, using one or more patterns that capture the typical ingredients of a noun phrase.
For example, here is some Wall Street Journal text with noun phrases marked using brackets:
| (10) | [ The/DT market/NN ] for/IN [ system-management/NN software/NN ] for/IN [ Digital/NNP ] [ 's/POS hardware/NN ] is/VBZ fragmented/JJ enough/RB that/IN [ a/DT giant/NN ] such/JJ as/IN [ Computer/NNP Associates/NNPS ] should/MD do/VB well/RB there/RB ./. |
From the point of view of theoretical linguistics, we seem to have been rather unorthodox in our use of the term "noun phrase"; although all the bracketed strings are noun phrases, not every noun phrase has been captured. We will discuss this issue in more detail shortly. For the moment, let's say that we are identifying noun "chunks" rather than full noun phrases.
In chunking, we carry out segmentation and labeling of multi-token sequences, as illustrated in Figure 6.1. The smaller boxes show word-level segmentation and labeling, while the large boxes show higher-level segmentation and labeling. It is these larger pieces that we will call chunks, and the process of identifying them is called chunking.

Figure 6.1: Segmentation and Labeling at both the Token and Chunk Levels
Like tokenization, chunking can skip over material in the input. Tokenization omits white space and punctuation characters. Chunking uses only a subset of the tokens and leaves others out.
In this chapter, we will explore chunking in some depth, beginning with the definition and representation of chunks. We will see regular expression and n-gram approaches to chunking, and will develop and evaluate chunkers using the CoNLL-2000 chunking corpus. Towards the end of the chapter, we will look more briefly at Named Entity Recognition and related tasks.
6.2 Defining and Representing Chunks
6.2.1 Chunking vs Parsing
Chunking is akin to parsing in the sense that it can be used to build hierarchical structure over text. There are several important differences, however. First, as noted above, chunking is not exhaustive, and typically ignores some items in the surface string. In fact, chunking is sometimes called partial parsing. Second, where parsing constructs nested structures that are arbitrarily deep, chunking creates structures of fixed depth (typically depth 2). These chunks often correspond to the lowest level of grouping identified in the full parse tree. This is illustrated in (11b) below, which shows an np chunk structure and a completely parsed counterpart:
| (11) |
|
A significant motivation for chunking is its robustness and efficiency relative to parsing. As we will see in Chapter 7, parsing has problems with robustness, given the difficulty in gaining broad coverage while minimizing ambiguity. Parsing is also relatively inefficient: the time taken to parse a sentence grows with the cube of the length of the sentence, while the time taken to chunk a sentence only grows linearly.
6.2.2 Representing Chunks: Tags vs Trees
As befits its intermediate status between tagging and parsing, chunk structures can be represented using either tags or trees. The most widespread file representation uses so-called IOB tags. In this scheme, each token is tagged with one of three special chunk tags, I (inside), O (outside), or B (begin). A token is tagged as B if it marks the beginning of a chunk. Subsequent tokens within the chunk are tagged I. All other tokens are tagged O. The B and I tags are suffixed with the chunk type, e.g. B-NP, I-NP. Of course, it is not necessary to specify a chunk type for tokens that appear outside a chunk, so these are just labeled O. An example of this scheme is shown in Figure 6.2.

Figure 6.2: Tag Representation of Chunk Structures
IOB tags have become the standard way to represent chunk structures in files, and we will also be using this format. Here is an example of the file representation of the information in Figure 6.2:
We PRP B-NP saw VBD O the DT B-NP little JJ I-NP yellow JJ I-NP dog NN I-NP
In this representation, there is one token per line, each with its part-of-speech tag and its chunk tag. We will see later that this format permits us to represent more than one chunk type, so long as the chunks do not overlap.
As we saw earlier, chunk structures can also be represented using trees. These have the benefit that each chunk is a constituent that can be manipulated directly. An example is shown in Figure 6.3:
Figure 6.3: Tree Representation of Chunk Structures
NLTK uses trees for its internal representation of chunks, and provides methods for reading and writing such trees to the IOB format. By now you should understand what chunks are, and how they are represented. In the next section, you will see how to build a simple chunker.
6.3 Chunking
A chunker finds contiguous, non-overlapping spans of related tokens and groups them together into chunks. Chunkers often operate on tagged texts, and use the tags to make chunking decisions. In this section we will see how to write a special type of regular expression over part-of-speech tags, and then how to combine these into a chunk grammar. Then we will set up a chunker to chunk some tagged text according to the grammar.
Chunking in NLTK begins with tagged tokens.
|
Next, we write regular expressions over tag sequences. The following example identifies noun phrases that consist of an optional determiner, followed by any number of adjectives, then a noun.
|
We create a chunker cp that can then be used repeatedly to parse tagged input. The result of chunking is a tree.
|
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint
6.3.1 Tag Patterns
A tag pattern is a sequence of part-of-speech tags delimited using angle brackets, e.g. <DT><JJ><NN>. Tag patterns are the same as the regular expression patterns we have already seen, except for two differences that make them easier to use for chunking. First, angle brackets group their contents into atomic units, so "<NN>+" matches one or more repetitions of the tag NN; and "<NN|JJ>" matches the NN or JJ. Second, the period wildcard operator is constrained not to cross tag delimiters, so that "<N.*>" matches any single tag starting with N, e.g. NN, NNS.
Now, consider the following noun phrases from the Wall Street Journal:
another/DT sharp/JJ dive/NN trade/NN figures/NNS any/DT new/JJ policy/NN measures/NNS earlier/JJR stages/NNS Panamanian/JJ dictator/NN Manuel/NNP Noriega/NNP
We can match these using a slight refinement of the first tag pattern above: <DT>?<JJ.*>*<NN.*>+. This can be used to chunk any sequence of tokens beginning with an optional determiner DT, followed by zero or more adjectives of any type JJ.* (including relative adjectives like earlier/JJR), followed by one or more nouns of any type NN.*. It is easy to find many more difficult examples:
his/PRP$ Mansion/NNP House/NNP speech/NN the/DT price/NN cutting/VBG 3/CD %/NN to/TO 4/CD %/NN more/JJR than/IN 10/CD %/NN the/DT fastest/JJS developing/VBG trends/NNS 's/POS skill/NN
Your challenge will be to come up with tag patterns to cover these and other examples. A good way to learn about tag patterns is via a graphical interface nltk.draw.rechunkparser.demo().
6.3.2 Chunking with Regular Expressions
The chunker begins with a flat structure in which no tokens are chunked. Patterns are applied in turn, successively updating the chunk structure. Once all of the patterns have been applied, the resulting chunk structure is returned. Listing 6.1 shows a simple chunk grammar consisting of two patterns. The first pattern matches an optional determiner or possessive pronoun (recall that | indicates disjunction), zero or more adjectives, then a noun. The second rule matches one or more proper nouns. We also define some tagged tokens to be chunked, and run the chunker on this input.
| ||
| ||
Listing 6.1 (chunker1.py): Simple Noun Phrase Chunker |
Note
The $ symbol is a special character in regular expressions, and therefore needs to be escaped with the backslash \ in order to match the tag PP$.
If a tag pattern matches at overlapping locations, the first match takes precedence. For example, if we apply a rule that matches two consecutive nouns to a text containing three consecutive nouns, then only the first two nouns will be chunked:
|
Once we have created the chunk for money market, we have removed the context that would have permitted fund to be included in a chunk. This issue would have been avoided with a more permissive chunk rule, e.g. NP: {<NN>+}.
6.3.3 Developing Chunkers
Creating a good chunker usually requires several rounds of development and testing, during which existing rules are refined and new rules are added. In order to diagnose any problems, it often helps to trace the execution of a chunker, using its trace argument. The tracing output shows the rules that are applied, and uses braces to show the chunks that are created at each stage of processing. In Listing 6.2, two chunk patterns are applied to the input sentence. The first rule finds all sequences of three tokens whose tags are DT, JJ, and NN, and the second rule finds any sequence of tokens whose tags are either DT or NN. We set up two chunkers, one for each rule ordering, and test them on the same input.
| ||
| ||
Listing 6.2 (chunker2.py): Two Noun Phrase Chunkers Having Identical Rules in Different Orders |
Observe that when we chunk material that is already partially chunked, the chunker will only create chunks that do not partially overlap existing chunks. In the case of cp2, the second rule did not find any chunks, since all chunks that matched its tag pattern overlapped with existing chunks. As you can see, you need to be careful to put chunk rules in the right order.
You may have noted that we have added explanatory comments, preceded by #, to each of our tag rules. Although it is not strictly necessary to do this, it's a helpful reminder of what a rule is meant to do, and it is used as a header line for the output of a rule application when tracing is on.
You might want to test out some of your rules on a corpus. One option is to use the Brown corpus. However, you need to remember that the Brown tagset is different from the Penn Treebank tagset that we have been using for our examples so far in this chapter; see Table 3.6 in Chapter 3 for a refresher. Because the Brown tagset uses NP for proper nouns, in this example we have followed Abney in labeling noun chunks as NX.
|
6.3.4 Exercises
- ☼ Chunk Grammar Development: Try developing a series of chunking rules using the graphical interface accessible via nltk.draw.rechunkparser.demo()
- ☼ Chunking Demonstration: Run the chunking demonstration: nltk.chunk.demo()
- ☼ IOB Tags: The IOB format categorizes tagged tokens as I, O and B. Why are three tags necessary? What problem would be caused if we used I and O tags exclusively?
- ☼ Write a tag pattern to match noun phrases containing plural head nouns, e.g. "many/JJ researchers/NNS", "two/CD weeks/NNS", "both/DT new/JJ positions/NNS". Try to do this by generalizing the tag pattern that handled singular noun phrases.
- ◑ Write a tag pattern to cover noun phrases that contain gerunds, e.g. "the/DT receiving/VBG end/NN", "assistant/NN managing/VBG editor/NN". Add these patterns to the grammar, one per line. Test your work using some tagged sentences of your own devising.
- ◑ Write one or more tag patterns to handle coordinated noun phrases, e.g. "July/NNP and/CC August/NNP", "all/DT your/PRP$ managers/NNS and/CC supervisors/NNS", "company/NN courts/NNS and/CC adjudicators/NNS".
6.4 Scaling Up
Now you have a taste of what chunking can do, but we have not explained how to carry out a quantitative evaluation of chunkers. For this, we need to get access to a corpus that has been annotated not only with parts-of-speech, but also with chunk information. We will begin by looking at the mechanics of converting IOB format into an NLTK tree, then at how this is done on a larger scale using a chunked corpus directly. We will see how to use the corpus to score the accuracy of a chunker, then look some more flexible ways to manipulate chunks. Our focus throughout will be on scaling up the coverage of a chunker.
6.4.1 Reading IOB Format and the CoNLL 2000 Corpus
Using the corpora module we can load Wall Street Journal text that has been tagged, then chunked using the IOB notation. The chunk categories provided in this corpus are np, vp and pp. As we have seen, each sentence is represented using multiple lines, as shown below:
he PRP B-NP accepted VBD B-VP the DT B-NP position NN I-NP ...
A conversion function chunk.conllstr2tree() builds a tree representation from one of these multi-line strings. Moreover, it permits us to choose any subset of the three chunk types to use. The example below produces only np chunks:
|

We can use the NLTK corpus module to access a larger amount of chunked text. The CoNLL 2000 corpus contains 270k words of Wall Street Journal text, divided into "train" and "test" portions, annotated with part-of-speech tags and chunk tags in the IOB format. We can access the data using an NLTK corpus reader called conll2000. Here is an example that reads the 100th sentence of the "train" portion of the corpus:
|
This showed three chunk types, for np, vp and pp. We can also select which chunk types to read:
|
6.4.2 Simple Evaluation and Baselines
Armed with a corpus, it is now possible to carry out some simple evaluation. We start off by establishing a baseline for the trivial chunk parser cp that creates no chunks:
|
This indicates that more than a third of the words are tagged with O (i.e., not in an np chunk). Now let's try a naive regular expression chunker that looks for tags (e.g., CD, DT, JJ, etc.) beginning with letters that are typical of noun phrase tags:
|
As you can see, this approach achieves pretty good results. In order to develop a more data-driven approach, let's define a function chunked_tags() that takes some chunked data and sets up a conditional frequency distribution. For each tag, it counts up the number of times the tag occurs inside an np chunk (the True case, where chtag is B-NP or I-NP), or outside a chunk (the False case, where chtag is O). It returns a list of those tags that occur inside chunks more often than outside chunks.
| ||
| ||
Listing 6.3 (chunker3.py): Capturing the conditional frequency of NP Chunk Tags |
The next step is to convert this list of tags into a tag pattern. To do this we need to "escape" all non-word characters, by preceding them with a backslash. Then we need to join them into a disjunction. This process would convert a tag list ['NN', 'NN\$'] into the tag pattern <NN|NN\$>. The following function does this work, and returns a regular expression chunker:
| ||
Listing 6.4 (chunker4.py): Deriving a Regexp Chunker from Training Data |
The final step is to train this chunker and test its accuracy (this time on the "test" portion of the corpus, i.e., data not seen during training):
|
6.4.3 Splitting and Merging (incomplete)
[Notes: the above approach creates chunks that are too large, e.g. the cat the dog chased would be given a single np chunk because it does not detect that determiners introduce new chunks. For this we would need a rule to split an np chunk prior to any determiner, using a pattern like: "NP: <.*>}{<DT>". We can also merge chunks, e.g. "NP: <NN>{}<NN>".]
6.4.4 Chinking
Sometimes it is easier to define what we don't want to include in a chunk than it is to define what we do want to include. In these cases, it may be easier to build a chunker using a method called chinking.
Following [Church, Young, & Bloothooft, 1996], we define a chink as a sequence of tokens that is not included in a chunk. In the following example, barked/VBD at/IN is a chink:
[ the/DT little/JJ yellow/JJ dog/NN ] barked/VBD at/IN [ the/DT cat/NN ]
Chinking is the process of removing a sequence of tokens from a chunk. If the sequence of tokens spans an entire chunk, then the whole chunk is removed; if the sequence of tokens appears in the middle of the chunk, these tokens are removed, leaving two chunks where there was only one before. If the sequence is at the beginning or end of the chunk, these tokens are removed, and a smaller chunk remains. These three possibilities are illustrated in Table 6.1.
| Entire chunk | Middle of a chunk | End of a chunk | |
| Input | [a/DT little/JJ dog/NN] | [a/DT little/JJ dog/NN] | [a/DT little/JJ dog/NN] |
| Operation | Chink "DT JJ NN" | Chink "JJ" | Chink "NN" |
| Pattern | "}DT JJ NN{" | "}JJ{" | "}NN{" |
| Output | a/DT little/JJ dog/NN | [a/DT] little/JJ [dog/NN] | [a/DT little/JJ] dog/NN |
In the following grammar, we put the entire sentence into a single chunk, then excise the chink:
| ||
| ||
Listing 6.5 (chinker.py): Simple Chinker |
A chunk grammar can use any number of chunking and chinking patterns in any order.
6.4.5 Multiple Chunk Types (incomplete)
So far we have only developed np chunkers. However, as we saw earlier in the chapter, the CoNLL chunking data is also annotated for pp and vp chunks. Here is an example, to show the structure we get from the corpus and the flattened version that will be used as input to the parser.
|
Now we can set up a multi-stage chunk grammar, as shown in Listing 6.6. It has a stage for each of the chunk types.
| ||
| ||
Listing 6.6 (multistage_chunker.py): A Multistage Chunker |
6.4.6 Evaluating Chunk Parsers
An easy way to evaluate a chunk parser is to take some already chunked text, strip off the chunks, rechunk it, and compare the result with the original chunked text. The ChunkScore.score() function takes the correctly chunked sentence as its first argument, and the newly chunked version as its second argument, and compares them. It reports the fraction of actual chunks that were found (recall), the fraction of hypothesized chunks that were correct (precision), and a combined score, the F-measure (the harmonic mean of precision and recall).
A number of different metrics can be used to evaluate chunk parsers. We will concentrate on a class of metrics that can be derived from two sets:
- guessed: The set of chunks returned by the chunk parser.
- correct: The correct set of chunks, as defined in the test corpus.
We will set up an analogy between the correct set of chunks and a user's so-called "information need", and between the set of returned chunks and a system's returned documents (cf precision and recall, from Chapter 4).
During evaluation of a chunk parser, it is useful to flatten a chunk structure into a tree consisting only of a root node and leaves:
|
We run a chunker over this flattened data, and compare the resulting chunked sentences with the originals, as follows:
|
ChunkScore is a class for scoring chunk parsers. It can be used to evaluate the output of a chunk parser, using precision, recall, f-measure, missed chunks, and incorrect chunks. It can also be used to combine the scores from the parsing of multiple texts. This is quite useful if we are parsing a text one sentence at a time. The following program listing shows a typical use of the ChunkScore class. In this example, chunkparser is being tested on each sentence from the Wall Street Journal tagged files.
|
The overall results of the evaluation can be viewed by printing the ChunkScore. Each evaluation metric is also returned by an accessor method: precision(), recall, f_measure, missed, and incorrect. The missed and incorrect methods can be especially useful when trying to improve the performance of a chunk parser. Here are the missed chunks:
|
Here are the incorrect chunks:
|
6.4.7 Exercises
- ◑ Chunker Evaluation:
Carry out the following evaluation tasks for
any of the chunkers you have developed earlier.
(Note that most chunking corpora contain some internal
inconsistencies, such that any reasonable rule-based approach
will produce errors.)
- Evaluate your chunker on 100 sentences from a chunked corpus, and report the precision, recall and F-measure.
- Use the chunkscore.missed() and chunkscore.incorrect() methods to identify the errors made by your chunker. Discuss.
- Compare the performance of your chunker to the baseline chunker discussed in the evaluation section of this chapter.
- ★ Transformation-Based Chunking: Apply the n-gram and Brill tagging methods to IOB chunk tagging. Instead of assigning POS tags to words, here we will assign IOB tags to the POS tags. E.g. if the tag DT (determiner) often occurs at the start of a chunk, it will be tagged B (begin). Evaluate the performance of these chunking methods relative to the regular expression chunking methods covered in this chapter.
6.4.8 Exercises
- ☼ Pick one of the three chunk types in the CoNLL corpus. Inspect the CoNLL corpus and try to observe any patterns in the POS tag sequences that make up this kind of chunk. Develop a simple chunker using the regular expression chunker nltk.RegexpParser. Discuss any tag sequences that are difficult to chunk reliably.
- ☼ An early definition of chunk was the material that occurs between chinks. Develop a chunker that starts by putting the whole sentence in a single chunk, and then does the rest of its work solely by chinking. Determine which tags (or tag sequences) are most likely to make up chinks with the help of your own utility program. Compare the performance and simplicity of this approach relative to a chunker based entirely on chunk rules.
- ◑ Develop a chunker for one of the chunk types in the CoNLL corpus using a regular-expression based chunk grammar RegexpChunk. Use any combination of rules for chunking, chinking, merging or splitting.
- ◑ Sometimes a word is incorrectly tagged, e.g. the head noun in "12/CD or/CC so/RB cases/VBZ". Instead of requiring manual correction of tagger output, good chunkers are able to work with the erroneous output of taggers. Look for other examples of correctly chunked noun phrases with incorrect tags.
- ★ We saw in the tagging chapter that it is possible to establish an upper limit to tagging performance by looking for ambiguous n-grams, n-grams that are tagged in more than one possible way in the training data. Apply the same method to determine an upper bound on the performance of an n-gram chunker.
- ★
Pick one of the three chunk types in the CoNLL corpus. Write functions
to do the following tasks for your chosen type:
- List all the tag sequences that occur with each instance of this chunk type.
- Count the frequency of each tag sequence, and produce a ranked list in order of decreasing frequency; each line should consist of an integer (the frequency) and the tag sequence.
- Inspect the high-frequency tag sequences. Use these as the basis for developing a better chunker.
- ★ The baseline chunker presented in the evaluation section tends to create larger chunks than it should. For example, the phrase: [every/DT time/NN] [she/PRP] sees/VBZ [a/DT newspaper/NN] contains two consecutive chunks, and our baseline chunker will incorrectly combine the first two: [every/DT time/NN she/PRP]. Write a program that finds which of these chunk-internal tags typically occur at the start of a chunk, then devise one or more rules that will split up these chunks. Combine these with the existing baseline chunker and re-evaluate it, to see if you have discovered an improved baseline.
- ★ Develop an np chunker that converts POS-tagged text into a list of tuples, where each tuple consists of a verb followed by a sequence of noun phrases and prepositions, e.g. the little cat sat on the mat becomes ('sat', 'on', 'NP')...
- ★
The Penn Treebank contains a section of tagged Wall Street Journal text
that has been chunked into noun phrases. The format uses square brackets,
and we have encountered it several times during this chapter.
The Treebank corpus can be accessed using:
for sent in nltk.corpus.treebank_chunk.chunked_sents(file). These are flat trees,
just as we got using nltk.corpus.conll2000.chunked_sents().
- The functions nltk.tree.pprint() and nltk.chunk.tree2conllstr() can be used to create Treebank and IOB strings from a tree. Write functions chunk2brackets() and chunk2iob() that take a single chunk tree as their sole argument, and return the required multi-line string representation.
- Write command-line conversion utilities bracket2iob.py and iob2bracket.py that take a file in Treebank or CoNLL format (resp) and convert it to the other format. (Obtain some raw Treebank or CoNLL data from the NLTK Corpora, save it to a file, and then use for line in open(filename) to access it from Python.)
6.5 N-Gram Chunking
Our approach to chunking has been to try to detect structure based on the part-of-speech tags. We have seen that the IOB format represents this extra structure using another kind of tag. The question arises as to whether we could use the same n-gram tagging methods we saw in Chapter 3, applied to a different vocabulary. In this case, rather than trying to determine the correct part-of-speech tag, given a word, we are trying to determine the correct chunk tag, given a part-of-speech tag.
The first step is to get the word,tag,chunk triples from the CoNLL 2000 corpus and map these to tag,chunk pairs:
|
We will now train two n-gram taggers over this data.
6.5.1 A Unigram Chunker
To start off, we train and score a unigram chunker on the above data, just as if it was a tagger:
|
This chunker does reasonably well. Let's look at the errors it makes. Consider the opening phrase of the first sentence of the CONLL chunking data, here shown with part-of-speech tags:
Confidence/NN in/IN the/DT pound/NN is/VBZ widely/RB expected/VBN to/TO take/VB another/DT sharp/JJ dive/NN
We can try out the unigram chunker on this first sentence by creating some "tokens" using [t for t,c in chunk_data[0]], then running our chunker over them using list(unigram_chunker.tag(tokens)). The unigram chunker only looks at the tags, and tries to add chunk tags. Here is what it comes up with:
NN/I-NP IN/B-PP DT/B-NP NN/I-NP VBZ/B-VP RB/O VBN/I-VP TO/B-PP VB/I-VP DT/B-NP JJ/I-NP NN/I-NP
Notice that it tags all instances of NN with I-NP, because nouns usually do not appear at the beginning of noun phrases in the training data. Thus, the first noun Confidence/NN is tagged incorrectly. However, pound/NN and dive/NN are correctly tagged as I-NP; they are not in the initial position that should be tagged B-NP. The chunker incorrectly tags widely/RB as O, and it incorrectly tags the infinitival to/TO as B-PP, as if it was a preposition starting a prepositional phrase.
6.5.2 A Bigram Chunker (incomplete)
[Why these problems might go away if we look at the previous chunk tag?]
Let's run a bigram chunker:
|
We can run the bigram chunker over the same sentence as before using list(bigram_chunker.tag(tokens)). Here is what it comes up with:
NN/B-NP IN/B-PP DT/B-NP NN/I-NP VBZ/B-VP RB/I-VP VBN/I-VP TO/I-VP VB/I-VP DT/B-NP JJ/I-NP NN/I-NP
This is 100% correct.
6.5.3 Exercises
- ◑ The bigram chunker scores about 90% accuracy. Study its errors and try to work out why it doesn't get 100% accuracy.
- ◑ Experiment with trigram chunking. Are you able to improve the performance any more?
- ★ An n-gram chunker can use information other than the current part-of-speech tag and the n-1 previous chunk tags. Investigate other models of the context, such as the n-1 previous part-of-speech tags, or some combination of previous chunk tags along with previous and following part-of-speech tags.
- ★ Consider the way an n-gram tagger uses recent tags to inform its tagging choice. Now observe how a chunker may re-use this sequence information. For example, both tasks will make use of the information that nouns tend to follow adjectives (in English). It would appear that the same information is being maintained in two places. Is this likely to become a problem as the size of the rule sets grows? If so, speculate about any ways that this problem might be addressed.
6.6 Cascaded Chunkers
So far, our chunk structures have been relatively flat. Trees consist of tagged tokens, optionally grouped under a chunk node such as NP. However, it is possible to build chunk structures of arbitrary depth, simply by creating a multi-stage chunk grammar. These stages are processed in the order that they appear. The patterns in later stages can refer to a mixture of part-of-speech tags and chunk types. Listing 6.7 has patterns for noun phrases, prepositional phrases, verb phrases, and sentences. This is a four-stage chunk grammar, and can be used to create structures having a depth of at most four.
| ||
| ||
Listing 6.7 (cascaded_chunker.py): A Chunker that Handles NP, PP, VP and S |
Unfortunately this result misses the vp headed by saw. It has other shortcomings too. Let's see what happens when we apply this chunker to a sentence having deeper nesting.
|
The solution to these problems is to get the chunker to loop over its patterns: after trying all of them, it repeats the process. We add an optional second argument loop to specify the number of times the set of patterns should be run:
|
This cascading process enables us to create deep structures. However, creating and debugging a cascade is quite difficult, and there comes a point where it is more effective to do full parsing (see Chapter 7).
6.7 Shallow Interpretation
The main form of shallow semantic interpretation that we will consider is Information Extraction. This refers to the task of converting unstructured data (e.g., unrestricted text) or semi-structured data (e.g., web pages marked up with HTML) into structured data (e.g., tables in a relational database). For example, let's suppose we are given a text containing the fragment (12), and let's also suppose we are trying to find pairs of entities X and Y that stand in the relation 'organization X is located in location Y'.
| (12) | ... said William Gale, an economist at the Brookings Institution, the research group in Washington. |
As a result of processing this text, we should be able to add the pair 〈Brookings Institution, Washington〉 to this relation. As we will see shortly, Information Extraction proceeds on the assumption that we are only looking for specific sorts of information, and these have been decided in advance. This limitation has been a necessary concession to allow the robust processing of unrestricted text.
Potential applications of Information Extraction are many, and include business intelligence, resume harvesting, media analysis, sentiment detection, patent search, and email scanning. A particularly important area of current research involves the attempt to extract structured data out of electronically-available scientific literature, most notably in the domain of biology and medicine.
Information Extraction is usually broken down into at least two major steps: Named Entity Recognition and Relation Extraction. Named Entities (NEs) are usually taken to be noun phrases that denote specific types of individuals such as organizations, persons, dates, and so on. Thus, we might use the following XML annotations to mark-up the NEs in (12):
| (13) | ... said <ne type='PERSON'>William Gale</ne>, an economist at the <ne type='ORGANIZATION'>Brookings Institution</ne>, the research group in <ne type='LOCATION'>Washington<ne>. |
How do we go about identifying NEs? Our first thought might be that we could look up candidate expressions in an appropriate list of names. For example, in the case of locations, we might try using a resource such as the Alexandria Gazetteer. Depending on the nature of our input data, this may be adequate — such a gazetteer is likely to have good coverage of international cities and many locations in the U.S.A., but will probably be missing the names of obscure villages in remote regions. However, a list of names for people or organizations will probably have poor coverage. New organizations, and new names for them, are coming into existence every day, so if we are trying to deal with contemporary newswire or blog entries, say, it is unlikely that we will be able to recognize many of the NEs by using gazetteer lookup.
A second consideration is that many NE terms are ambiguous. Thus May and North are likely to be parts of NEs for DATE and LOCATION, respectively, but could both be part of a PERSON NE; conversely Christian Dior looks like a PERSON NE but is more likely to be of type ORGANIZATION. A term like Yankee will be ordinary modifier in some contexts, but will be marked as an NE of type ORGANIZATION in the phrase Yankee infielders. To summarize, we cannot reliably detect NEs by looking them up in a gazetteer, and it is also hard to develop rules that will correctly recognize ambiguous NEs on the basis of their context of occurrence. Although lookup may contribute to a solution, most contemporary approaches to Named Entity Recognition treat it as a statistical classification task that requires training data for good performance. This task is facilitated by adopting an appropriate data representation, such as the IOB tags that we saw being deployed in the CoNLL chunk data (Chapter 6). For example, here are a representative few lines from the CONLL 2002 (conll2002) Dutch training data:
Eddy N B-PER Bonte N I-PER is V O woordvoerder N O van Prep O diezelfde Pron O Hogeschool N B-ORG . Punc O
As noted before, in this representation, there is one token per line, each with its part-of-speech tag and its NE tag. When NEs have been identified in a text, we then want to extract relations that hold between them. As indicated earlier, we will typically be looking for relations between specified types of NE. One way of approaching this task is to initially look for all triples of the form X, α, Y, where X and Y are NEs of the required types, and α is the string of words that intervenes between X and Y. We can then use regular expressions to pull out just those instances of α that express the relation that we are looking for. The following example searches for strings that contain the word in. The special character expression (?!\b.+ing\b) is a negative lookahead condition that allows us to disregard strings such as success in supervising the transition of, where in is followed by a gerundive verb.
|
Searching for the keyword works in reasonably well, though it will also retrieve false positives such as [ORG: House Transportation Committee] , secured the most money in the [LOC: New York]; there is unlikely to be simple string-based method of excluding filler strings such as this.
|
6.8 Conclusion
In this chapter we have explored efficient and robust methods that can identify linguistic structures in text. Using only part-of-speech information for words in the local context, a "chunker" can successfully identify simple structures such as noun phrases and verb groups. We have seen how chunking methods extend the same lightweight methods that were successful in tagging. The resulting structured information is useful in information extraction tasks and in the description of the syntactic environments of words. The latter will be invaluable as we move to full parsing.
There are a surprising number of ways to chunk a sentence using regular expressions. The patterns can add, shift and remove chunks in many ways, and the patterns can be sequentially ordered in many ways. One can use a small number of very complex rules, or a long sequence of much simpler rules. One can hand-craft a collection of rules, and one can write programs to analyze a chunked corpus to help in the development of such rules. The process is painstaking, but generates very compact chunkers that perform well and that transparently encode linguistic knowledge.
It is also possible to chunk a sentence using the techniques of n-gram tagging. Instead of assigning part-of-speech tags to words, we assign IOB tags to the part-of-speech tags. Bigram tagging turned out to be particularly effective, as it could be sensitive to the chunk tag on the previous word. This statistical approach requires far less effort than rule-based chunking, but creates large models and delivers few linguistic insights.
Like tagging, chunking cannot be done perfectly. For example, as pointed out by [Church, Young, & Bloothooft, 1996], we cannot correctly analyze the structure of the sentence I turned off the spectroroute without knowing the meaning of spectroroute; is it a kind of road or a type of device? Without knowing this, we cannot tell whether off is part of a prepositional phrase indicating direction (tagged B-PP), or whether off is part of the verb-particle construction turn off (tagged I-VP).
A recurring theme of this chapter has been diagnosis. The simplest kind is manual, when we inspect the tracing output of a chunker and observe some undesirable behavior that we would like to fix. Sometimes we discover cases where we cannot hope to get the correct answer because the part-of-speech tags are too impoverished and do not give us sufficient information about the lexical item. A second approach is to write utility programs to analyze the training data, such as counting the number of times a given part-of-speech tag occurs inside and outside an np chunk. A third approach is to evaluate the system against some gold standard data to obtain an overall performance score. We can even use this to parameterize the system, specifying which chunk rules are used on a given run, and tabulating performance for different parameter combinations. Careful use of these diagnostic methods permits us to optimize the performance of our system. We will see this theme emerge again later in chapters dealing with other topics in natural language processing.
6.9 Further Reading
For more examples of chunking with NLTK, please see the guide at http://nltk.org/doc/guides/chunk.html.
The popularity of chunking is due in great part to pioneering work by Abney e.g., [Church, Young, & Bloothooft, 1996]. Abney's Cass chunker is available at http://www.vinartus.net/spa/97a.pdf
The word chink initially meant a sequence of stopwords, according to a 1975 paper by Ross and Tukey [Church, Young, & Bloothooft, 1996].
The IOB format (or sometimes BIO Format) was developed for np chunking by [Ramshaw & Marcus, 1995], and was used for the shared np bracketing task run by the Conference on Natural Language Learning (CoNLL) in 1999. The same format was adopted by CoNLL 2000 for annotating a section of Wall Street Journal text as part of a shared task on np chunking.
Section 13.5 of [Jurafsky & Martin, 2008] contains a discussion of chunking.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
7 Context Free Grammars and Parsing
7.1 Introduction
Early experiences with the kind of grammar taught in school are sometimes perplexing. Your written work might have been graded by a teacher who red-lined all the grammar errors they wouldn't put up with. Like the plural pronoun or the dangling preposition in the last sentence, or sentences like this one that lack a main verb. If you learnt English as a second language, you might have found it difficult to discover which of these errors need to be fixed (or needs to be fixed?). Correct punctuation is an obsession for many writers and editors. It is easy to find cases where changing punctuation changes meaning. In the following example, the interpretation of a relative clause as restrictive or non-restrictive depends on the presence of commas alone:
| (14) |
|
In (14a), we assume there is just one presidential candidate, and say two things about her: that she was popular and that she smiled. In (14b), on the other hand, we use the description who was extremely popular as a means of identifying which of several possible candidates we are referring to.
It is clear that some of these rules are important. However, others seem to be vestiges of antiquated style. Consider the injunction that however — when used to mean nevertheless — must not appear at the start of a sentence. Pullum argues that Strunk and White [Strunk & White, 1999] were merely insisting that English usage should conform to "an utterly unimportant minor statistical detail of style concerning adverb placement in the literature they knew" [Pullum, 2005]. This is a case where, a descriptive observation about language use became a prescriptive requirement. In NLP we usually discard such prescriptions, and use grammar to formalize observations about language as it is used, particularly as it is used in corpora.
In this chapter we present the fundamentals of syntax, focusing on constituency and tree representations, before describing the formal notation of context free grammar. Next we present parsers as an automatic way to associate syntactic structures with sentences. Finally, we give a detailed presentation of simple top-down and bottom-up parsing algorithms available in NLTK. Before launching into the theory we present some more naive observations about grammar, for the benefit of readers who do not have a background in linguistics.
7.2 More Observations about Grammar
Another function of a grammar is to explain our observations about ambiguous sentences. Even when the individual words are unambiguous, we can put them together to create ambiguous sentences, as in (15b).
| (15) |
|
A grammar will be able to assign two structures to each sentence, accounting for the two possible interpretations.
Perhaps another kind of syntactic variation, word order, is easier to understand. We know that the two sentences Kim likes Sandy and Sandy likes Kim have different meanings, and that likes Sandy Kim is simply ungrammatical. Similarly, we know that the following two sentences are equivalent:
| (16) |
|
However, consider the semantically similar verbs filled and dumped. Now the word order cannot be altered (ungrammatical sentences are prefixed with an asterisk.)
| (17) |
|
A further notable fact is that we have no difficulty accessing the meaning of sentences we have never encountered before. It is not difficult to concoct an entirely novel sentence, one that has probably never been used before in the history of the language, and yet all speakers of the language will agree about its meaning. In fact, the set of possible sentences is infinite, given that there is no upper bound on length. Consider the following passage from a children's story, containing a rather impressive sentence:
You can imagine Piglet's joy when at last the ship came in sight of him. In after-years he liked to think that he had been in Very Great Danger during the Terrible Flood, but the only danger he had really been in was the last half-hour of his imprisonment, when Owl, who had just flown up, sat on a branch of his tree to comfort him, and told him a very long story about an aunt who had once laid a seagull's egg by mistake, and the story went on and on, rather like this sentence, until Piglet who was listening out of his window without much hope, went to sleep quietly and naturally, slipping slowly out of the window towards the water until he was only hanging on by his toes, at which moment, luckily, a sudden loud squawk from Owl, which was really part of the story, being what his aunt said, woke the Piglet up and just gave him time to jerk himself back into safety and say, "How interesting, and did she?" when -- well, you can imagine his joy when at last he saw the good ship, Brain of Pooh (Captain, C. Robin; 1st Mate, P. Bear) coming over the sea to rescue him... (from A.A. Milne In which Piglet is Entirely Surrounded by Water)
Our ability to produce and understand entirely new sentences, of arbitrary length, demonstrates that the set of well-formed sentences in English is infinite. The same case can be made for any human language.
This chapter presents grammars and parsing, as the formal and computational methods for investigating and modeling the linguistic phenomena we have been touching on (or tripping over). As we shall see, patterns of well-formedness and ill-formedness in a sequence of words can be understood with respect to the underlying phrase structure of the sentences. We can develop formal models of these structures using grammars and parsers. As before, the motivation is natural language understanding. How much more of the meaning of a text can we access when we can reliably recognize the linguistic structures it contains? Having read in a text, can a program 'understand' it enough to be able to answer simple questions about "what happened" or "who did what to whom." Also as before, we will develop simple programs to process annotated corpora and perform useful tasks.
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint
7.3 What's the Use of Syntax?
Earlier chapters focused on words: how to identify them, how to analyze their morphology, and how to assign them to classes via part-of-speech tags. We have also seen how to identify recurring sequences of words (i.e. n-grams). Nevertheless, there seem to be linguistic regularities that cannot be described simply in terms of n-grams.
In this section we will see why it is useful to have some kind of syntactic representation of sentences. In particular, we will see that there are systematic aspects of meaning that are much easier to capture once we have established a level of syntactic structure.
7.3.1 Syntactic Ambiguity
We have seen that sentences can be ambiguous. If we overheard someone say I went to the bank, we wouldn't know whether it was a river bank or a financial institution. This ambiguity concerns the meaning of the word bank, and is a kind of lexical ambiguity.
However, other kinds of ambiguity cannot be explained in terms of ambiguity of specific words. Consider a phrase involving an adjective with a conjunction: old men and women. Does old have wider scope than and, or is it the other way round? In fact, both interpretations are possible, and we can represent the different scopes using parentheses:
| (18) |
|
One convenient way of representing this scope difference at a structural level is by means of a tree diagram, as shown in (19b).
| (19) |
|
Note that linguistic trees grow upside down: the node labeled s is the root of the tree, while the leaves of the tree are labeled with the words.
In NLTK, you can easily produce trees like this yourself with the following commands:
|
We can construct other examples of syntactic ambiguity involving the coordinating conjunctions and and or, e.g. Kim left or Dana arrived and everyone cheered. We can describe this ambiguity in terms of the relative semantic scope of or and and.
For our third illustration of ambiguity, we look at prepositional phrases. Consider a sentence like: I saw the man with a telescope. Who has the telescope? To clarify what is going on here, consider the following pair of sentences:
| (20) |
|
In both cases, there is a prepositional phrase introduced by with. In the first case this phrase modifies the noun burglar, and in the second case it modifies the verb saw. We could again think of this in terms of scope: does the prepositional phrase (pp) just have scope over the np a burglar, or does it have scope over the whole verb phrase? As before, we can represent the difference in terms of tree structure:
| (21) |
|
In (21b)a, the pp attaches to the np, while in (21b)b, the pp attaches to the vp.
We can generate these trees in Python as follows:
|
We can discard the structure to get the list of leaves, and we can confirm that both trees have the same leaves (except for the last word). We can also see that the trees have different heights (given by the number of nodes in the longest branch of the tree, starting at s and descending to the words):
|
In general, how can we determine whether a prepositional phrase modifies the preceding noun or verb? This problem is known as prepositional phrase attachment ambiguity. The Prepositional Phrase Attachment Corpus makes it possible for us to study this question systematically. The corpus is derived from the IBM-Lancaster Treebank of Computer Manuals and from the Penn Treebank, and distills out only the essential information about pp attachment. Consider the sentence from the WSJ in (22a). The corresponding line in the Prepositional Phrase Attachment Corpus is shown in (22b).
| (22) |
|
That is, it includes an identifier for the original sentence, the head of the relevant verb phrase (i.e., including), the head of the verb's np object (three), the preposition (with), and the head noun within the prepositional phrase (cancer). Finally, it contains an "attachment" feature (N or V) to indicate whether the prepositional phrase attaches to (modifies) the noun phrase or the verb phrase. Here are some further examples:
| (23) | 47830 allow visits between families N 47830 allow visits on peninsula V 42457 acquired interest in firm N 42457 acquired interest in 1986 V |
The PP attachments in (23) can also be made explicit by using phrase groupings as in (24).
| (24) | allow (NP visits (PP between families)) allow (NP visits) (PP on peninsula) acquired (NP interest (PP in firm)) acquired (NP interest) (PP in 1986) |
Observe in each case that the argument of the verb is either a single complex expression (visits (between families)) or a pair of simpler expressions (visits) (on peninsula).
We can access the Prepositional Phrase Attachment Corpus from NLTK as follows:
|
If we go back to our first examples of pp attachment ambiguity, it appears as though it is the pp itself (e.g., with a gun versus with a telescope) that determines the attachment. However, we can use this corpus to find examples where other factors come into play. For example, it appears that the verb is the key factor in (25).
| (25) | 8582 received offer from group V 19131 rejected offer from group N |
7.3.2 Constituency
We claimed earlier that one of the motivations for building syntactic structure was to help make explicit how a sentence says "who did what to whom". Let's just focus for a while on the "who" part of this story: in other words, how can syntax tell us what the subject of a sentence is? At first, you might think this task is rather simple — so simple indeed that we don't need to bother with syntax. In a sentence such as The fierce dog bit the man we know that it is the dog that is doing the biting. So we could say that the noun phrase immediately preceding the verb is the subject of the sentence. And we might try to make this more explicit in terms of sequences part-of-speech tags. Let's try to come up with a simple definition of noun phrase; we might start off with something like this, based on our knowledge of noun phrase chunking (Chapter 6):
| (26) | dt jj* nn |
We're using regular expression notation here in the form of jj* to indicate a sequence of zero or more jjs. So this is intended to say that a noun phrase can consist of a determiner, possibly followed by some adjectives, followed by a noun. Then we can go on to say that if we can find a sequence of tagged words like this that precedes a word tagged as a verb, then we've identified the subject. But now think about this sentence:
| (27) | The child with a fierce dog bit the man. |
This time, it's the child that is doing the biting. But the tag sequence preceding the verb is:
| (28) | dt nn in dt jj nn |
Our previous attempt at identifying the subject would have incorrectly come up with the fierce dog as the subject. So our next hypothesis would have to be a bit more complex. For example, we might say that the subject can be identified as any string matching the following pattern before the verb:
| (29) | dt jj* nn (in dt jj* nn)* |
In other words, we need to find a noun phrase followed by zero or more sequences consisting of a preposition followed by a noun phrase. Now there are two unpleasant aspects to this proposed solution. The first is esthetic: we are forced into repeating the sequence of tags (dt jj* nn) that constituted our initial notion of noun phrase, and our initial notion was in any case a drastic simplification. More worrying, this approach still doesn't work! For consider the following example:
| (30) | The seagull that attacked the child with the fierce dog bit the man. |
This time the seagull is the culprit, but it won't be detected as subject by our attempt to match sequences of tags. So it seems that we need a richer account of how words are grouped together into patterns, and a way of referring to these groupings at different points in the sentence structure. This idea of grouping is often called syntactic constituency.
As we have just seen, a well-formed sentence of a language is more than an arbitrary sequence of words from the language. Certain kinds of words usually go together. For instance, determiners like the are typically followed by adjectives or nouns, but not by verbs. Groups of words form intermediate structures called phrases or constituents. These constituents can be identified using standard syntactic tests, such as substitution, movement and coordination. For example, if a sequence of words can be replaced with a pronoun, then that sequence is likely to be a constituent. According to this test, we can infer that the italicized string in the following example is a constituent, since it can be replaced by they:
| (31) |
|
In order to identify whether a phrase is the subject of a sentence, we can use the construction called Subject-Auxiliary Inversion in English. This construction allows us to form so-called Yes-No Questions. That is, corresponding to the statement in (32a), we have the question in (32b):
| (32) |
|
Roughly speaking, if a sentence already contains an auxiliary verb, such as has in (32a), then we can turn it into a Yes-No Question by moving the auxiliary verb 'over' the subject noun phrase to the front of the sentence. If there is no auxiliary in the statement, then we insert the appropriate form of do as the fronted auxiliary and replace the tensed main verb by its base form:
| (33) |
|
As we would hope, this test also confirms our earlier claim about the subject constituent of (30):
| (34) | Did the seagull that attacked the child with the fierce dog bite the man? |
To sum up then, we have seen that the notion of constituent brings a number of benefits. By having a constituent labeled noun phrase, we can provide a unified statement of the classes of word that constitute that phrase, and reuse this statement in describing noun phrases wherever they occur in the sentence. Second, we can use the notion of a noun phrase in defining the subject of sentence, which in turn is a crucial ingredient in determining the "who does what to whom" aspect of meaning.
7.3.3 More on Trees
A tree is a set of connected nodes, each of which is labeled with a category. It common to use a 'family' metaphor to talk about the relationships of nodes in a tree: for example, s is the parent of vp; conversely vp is a daughter (or child) of s. Also, since np and vp are both daughters of s, they are also sisters. Here is an example of a tree:
| (35) |  |
Although it is helpful to represent trees in a graphical format, for computational purposes we usually need a more text-oriented representation. We will use the same format as the Penn Treebank, a combination of brackets and labels:
|
Here, the node value is a constituent type (e.g., np or vp), and the children encode the hierarchical contents of the tree.
Although we will focus on syntactic trees, trees can be used to encode any homogeneous hierarchical structure that spans a sequence of linguistic forms (e.g. morphological structure, discourse structure). In the general case, leaves and node values do not have to be strings.
In NLTK, trees are created with the Tree constructor, which takes a node value and a list of zero or more children. Here's a couple of simple trees:
|
We can incorporate these into successively larger trees as follows:
|
Here are some of the methods available for tree objects:
|
The printed representation for complex trees can be difficult to read. In these cases, the draw method can be very useful. It opens a new window, containing a graphical representation of the tree. The tree display window allows you to zoom in and out; to collapse and expand subtrees; and to print the graphical representation to a postscript file (for inclusion in a document).
|
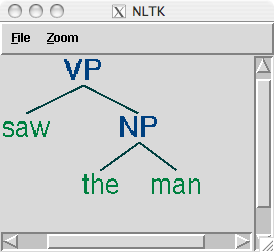
7.3.4 Treebanks (notes)
The corpus module defines the treebank corpus reader, which contains a 10% sample of the Penn Treebank corpus.
|
Listing 7.1 prints a tree object using whitespace formatting.
| ||
| ||
NLTK also includes a sample from the Sinica Treebank Corpus, consisting of 10,000 parsed sentences drawn from the Academia Sinica Balanced Corpus of Modern Chinese. Here is a code fragment to read and display one of the trees in this corpus.
|
| (36) | 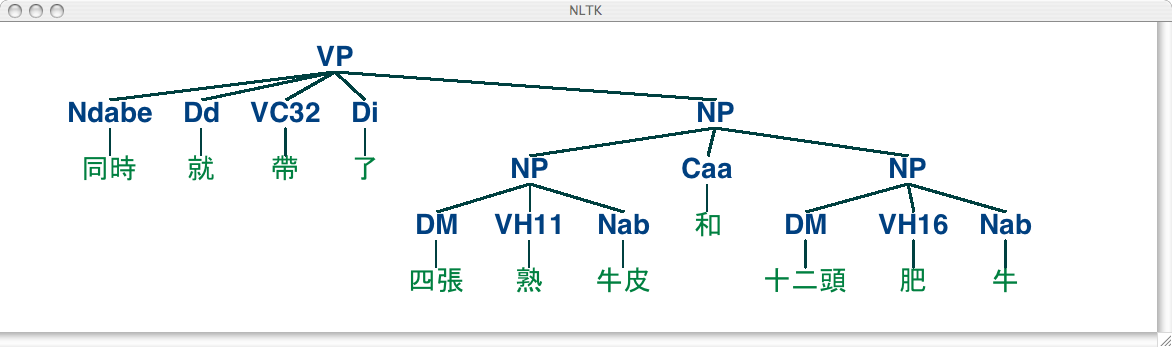 |
Note that we can read tagged text from a Treebank corpus, using the tagged() method:
|
7.3.5 Exercises
☼ Can you come up with grammatical sentences that have probably never been uttered before? (Take turns with a partner.) What does this tell you about human language?
☼ Recall Strunk and White's prohibition against sentence-initial however used to mean "although". Do a web search for however used at the start of the sentence. How widely used is this construction?
☼ Consider the sentence Kim arrived or Dana left and everyone cheered. Write down the parenthesized forms to show the relative scope of and and or. Generate tree structures corresponding to both of these interpretations.
☼ The Tree class implements a variety of other useful methods. See the Tree help documentation for more details, i.e. import the Tree class and then type help(Tree).
☼ Building trees:
- Write code to produce two trees, one for each reading of the phrase old men and women
- Encode any of the trees presented in this chapter as a labeled bracketing and use nltk.bracket_parse() to check that it is well-formed. Now use draw() to display the tree.
- As in (a) above, draw a tree for The woman saw a man last Thursday.
☼ Write a recursive function to traverse a tree and return the depth of the tree, such that a tree with a single node would have depth zero. (Hint: the depth of a subtree is the maximum depth of its children, plus one.)
☼ Analyze the A.A. Milne sentence about Piglet, by underlining all of the sentences it contains then replacing these with s (e.g. the first sentence becomes s when:lx` s). Draw a tree structure for this "compressed" sentence. What are the main syntactic constructions used for building such a long sentence?
◑ To compare multiple trees in a single window, we can use the draw_trees() method. Define some trees and try it out:
>>> from nltk.draw.tree import draw_trees >>> draw_trees(tree1, tree2, tree3)
◑ Using tree positions, list the subjects of the first 100 sentences in the Penn treebank; to make the results easier to view, limit the extracted subjects to subtrees whose height is 2.
◑ Inspect the Prepositional Phrase Attachment Corpus and try to suggest some factors that influence pp attachment.
◑ In this section we claimed that there are linguistic regularities that cannot be described simply in terms of n-grams. Consider the following sentence, particularly the position of the phrase in his turn. Does this illustrate a problem for an approach based on n-grams?
What was more, the in his turn somewhat youngish Nikolay Parfenovich also turned out to be the only person in the entire world to acquire a sincere liking to our "discriminated-against" public procurator. (Dostoevsky: The Brothers Karamazov)
◑ Write a recursive function that produces a nested bracketing for a tree, leaving out the leaf nodes, and displaying the non-terminal labels after their subtrees. So the above example about Pierre Vinken would produce: [[[NNP NNP]NP , [ADJP [CD NNS]NP JJ]ADJP ,]NP-SBJ MD [VB [DT NN]NP [IN [DT JJ NN]NP]PP-CLR [NNP CD]NP-TMP]VP .]S Consecutive categories should be separated by space.
- ◑ Download several electronic books from Project Gutenberg. Write a program to scan these texts for any extremely long sentences. What is the longest sentence you can find? What syntactic construction(s) are responsible for such long sentences?
- ★ One common way of defining the subject of a sentence s in English is as the noun phrase that is the daughter of s and the sister of vp. Write a function that takes the tree for a sentence and returns the subtree corresponding to the subject of the sentence. What should it do if the root node of the tree passed to this function is not s, or it lacks a subject?
7.4 Context Free Grammar
As we have seen, languages are infinite — there is no principled upper-bound on the length of a sentence. Nevertheless, we would like to write (finite) programs that can process well-formed sentences. It turns out that we can characterize what we mean by well-formedness using a grammar. The way that finite grammars are able to describe an infinite set uses recursion. (We already came across this idea when we looked at regular expressions: the finite expression a+ is able to describe the infinite set {a, aa, aaa, aaaa, ...}). Apart from their compactness, grammars usually capture important structural and distributional properties of the language, and can be used to map between sequences of words and abstract representations of meaning. Even if we were to impose an upper bound on sentence length to ensure the language was finite, we would probably still want to come up with a compact representation in the form of a grammar.
A grammar is a formal system that specifies which sequences of words are well-formed in the language, and that provides one or more phrase structures for well-formed sequences. We will be looking at context-free grammar (CFG), which is a collection of productions of the form s → np vp. This says that a constituent s can consist of sub-constituents np and vp. Similarly, the production v → 'saw' | ``'walked' means that the constituent v can consist of the string saw or walked. For a phrase structure tree to be well-formed relative to a grammar, each non-terminal node and its children must correspond to a production in the grammar.
7.4.1 A Simple Grammar
Let's start off by looking at a simple context-free grammar. By convention, the left-hand-side of the first production is the start-symbol of the grammar, and all well-formed trees must have this symbol as their root label.
| (37) | S → NP VP
NP → Det N | Det N PP
VP → V | V NP | V NP PP
PP → P NP
Det → 'the' | 'a'
N → 'man' | 'park' | 'dog' | 'telescope'
V → 'saw' | 'walked'
P → 'in' | 'with'
|
This grammar contains productions involving various syntactic categories, as laid out in Table 7.1.
| Symbol | Meaning | Example |
|---|---|---|
| S | sentence | the man walked |
| NP | noun phrase | a dog |
| VP | verb phrase | saw a park |
| PP | prepositional phrase | with a telescope |
| ... | ... | ... |
| Det | determiner | the |
| N | noun | dog |
| V | verb | walked |
| P | preposition | in |
In our following discussion of grammar, we will use the following terminology. The grammar consists of productions, where each production involves a single non-terminal (e.g. s, np), an arrow, and one or more non-terminals and terminals (e.g. walked). The productions are often divided into two main groups. The grammatical productions are those without a terminal on the right hand side. The lexical productions are those having a terminal on the right hand side. A special case of non-terminals are the pre-terminals, which appear on the left-hand side of lexical productions. We will say that a grammar licenses a tree if each non-terminal x with children y1 ... yn corresponds to a production in the grammar of the form: x → y1 ... yn.
In order to get started with developing simple grammars of your own, you will probably find it convenient to play with the recursive descent parser demo, nltk.draw.rdparser.demo(). The demo opens a window that displays a list of grammar productions in the left hand pane and the current parse diagram in the central pane:
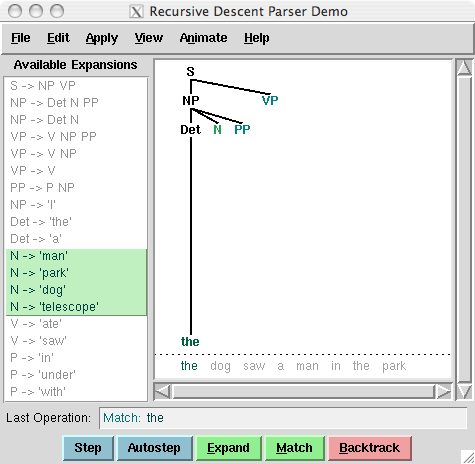
The demo comes with the grammar in (37) already loaded. We will discuss the parsing algorithm in greater detail below, but for the time being you can get an idea of how it works by using the autostep button. If we parse the string The dog saw a man in the park using the grammar in (37), we end up with two trees:
| (38) |
|
Since our grammar licenses two trees for this sentence, the sentence is said to be structurally ambiguous. The ambiguity in question is called a prepositional phrase attachment ambiguity, as we saw earlier in this chapter. As you may recall, it is an ambiguity about attachment since the pp in the park needs to be attached to one of two places in the tree: either as a daughter of VP or else as a daughter of np. When the pp is attached to vp, the seeing event happened in the park. However, if the pp is attached to np, then the man was in the park, and the agent of the seeing (the dog) might have been sitting on the balcony of an apartment overlooking the park. As we will see, dealing with ambiguity is a key challenge in parsing.
7.4.2 Recursion in Syntactic Structure
Observe that sentences can be nested within sentences, with no limit to the depth:
| (39) |
|
This nesting is explained in terms of recursion. A grammar is said to be recursive if a category occurring on the left hand side of a production (such as s in this case) also appears on the right hand side of a production. If this dual occurrence takes place in one and the same production, then we have direct recursion; otherwise we have indirect recursion. There is no recursion in (37). However, the grammar in (40) illustrates both kinds of recursive production:
| (40) | S → NP VP NP → Det Nom | Det Nom PP | PropN Nom → Adj Nom | N VP → V | V NP | V NP PP | V S PP → P NP PropN → 'John' | 'Mary' Det → 'the' | 'a' N → 'man' | 'woman' | 'park' | 'dog' | 'lead' | 'telescope' | 'butterfly' Adj → 'fierce' | 'black' | 'big' | 'European' V → 'saw' | 'chased' | 'barked' | 'disappeared' | 'said' | 'reported' P → 'in' | 'with' |
Notice that the production Nom → Adj Nom (where Nom is the category of nominals) involves direct recursion on the category Nom, whereas indirect recursion on s arises from the combination of two productions, namely s → np vp and vp → v s.
To see how recursion is handled in this grammar, consider the following trees. Example nested-nominals involves nested nominal phrases, while nested-sentences contains nested sentences.
| (41) |
|
If you did the exercises for the last section, you will have noticed that the recursive descent parser fails to deal properly with the following production: np → np pp. From a linguistic point of view, this production is perfectly respectable, and will allow us to derive trees like this:
| (42) | 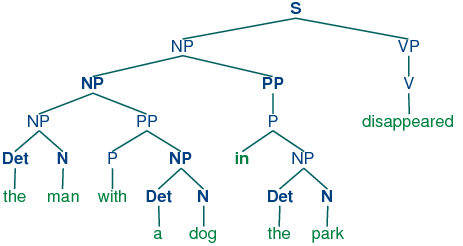 |
More schematically, the trees for these compound noun phrases will be of the following shape:
| (43) |  |
The structure in (43) is called a left recursive structure. These occur frequently in analyses of English, and the failure of recursive descent parsers to deal adequately with left recursion means that we will need to find alternative approaches.
7.4.3 Heads, Complements and Modifiers
Let us take a closer look at verbs. The grammar (40) correctly generates examples like (44d), corresponding to the four productions with vp on the left hand side:
| (44) |
|
That is, gave can occur with a following np and pp; saw can occur with a following np; said can occur with a following s; and barked can occur with no following phrase. In these cases, np, pp and s are called complements of the respective verbs, and the verbs themselves are called heads of the verb phrase.
However, there are fairly strong constraints on what verbs can occur with what complements. Thus, we would like our grammars to mark the following examples as ungrammatical [1]:
| (45) |
|
| [1] | It should be borne in mind that it is possible to create examples that involve 'non-standard' but interpretable combinations of verbs and complements. Thus, we can, at a stretch, interpret the man disappeared the dog as meaning that the man made the dog disappear. We will ignore such examples here. |
How can we ensure that our grammar correctly excludes the ungrammatical examples in (45d)? We need some way of constraining grammar productions which expand vp so that verbs only co-occur with their correct complements. We do this by dividing the class of verbs into subcategories, each of which is associated with a different set of complements. For example, transitive verbs such as saw, kissed and hit require a following np object complement. Borrowing from the terminology of chemistry, we sometimes refer to the valency of a verb, that is, its capacity to combine with a sequence of arguments and thereby compose a verb phrase.
Let's introduce a new category label for such verbs, namely tv (for Transitive Verb), and use it in the following productions:
| (46) | vp → tv np tv → 'saw' | 'kissed' | 'hit' |
Now *the dog barked the man is excluded since we haven't listed barked as a V_tr, but the woman saw a man is still allowed. Table 7.2 provides more examples of labels for verb subcategories.
| Symbol | Meaning | Example |
|---|---|---|
| IV | intransitive verb | barked |
| TV | transitive verb | saw a man |
| DatV | dative verb | gave a dog to a man |
| SV | sentential verb | said that a dog barked |
The revised grammar for vp will now look like this:
| (47) | vp → datv np pp vp → tv np vp → sv s vp → iv datv → 'gave' | 'donated' | 'presented' tv → 'saw' | 'kissed' | 'hit' | 'sang' sv → 'said' | 'knew' | 'alleged' iv → 'barked' | 'disappeared' | 'elapsed' | 'sang' |
Notice that according to (47), a given lexical item can belong to more than one subcategory. For example, sang can occur both with and without a following np complement.
7.4.4 Dependency Grammar
Although we concentrate on phrase structure grammars in this chapter, we should mention an alternative approach, namely dependency grammar. Rather than taking starting from the grouping of words into constituents, dependency grammar takes as basic the notion that one word can be dependent on another (namely, its head). The root of a sentence is usually taken to be the main verb, and every other word is either dependent on the root, or connects to it through a path of dependencies. Figure (48) illustrates a dependency graph, where the head of the arrow points to the head of a dependency.
| (48) |  |
As you will see, the arcs in Figure (48) are labeled with the particular dependency relation that holds between a dependent and its head. For example, Esso bears the subject relation to said (which is the head of the whole sentence), and Tuesday bears a verbal modifier (vmod) relation to started.
An alternative way of representing the dependency relationships is illustrated in the tree (49), where dependents are shown as daughters of their heads.
| (49) |  |
One format for encoding dependency information places each word on a line, followed by its part-of-speech tag, the index of its head, and the label of the dependency relation (cf. [Nivre, Hall, & Nilsson, 2006]). The index of a word is implicitly given by the ordering of the lines (with 1 as the first index). This is illustrated in the following code snippet:
|
As you will see, this format also adopts the convention that the head of the sentence is dependent on an empty node, indexed as 0. We can use the deptree() method of a DepGraph() object to build an NLTK tree like that illustrated earlier in (49).
|
7.4.5 Formalizing Context Free Grammars
We have seen that a CFG contains terminal and nonterminal symbols, and productions that dictate how constituents are expanded into other constituents and words. In this section, we provide some formal definitions.
A CFG is a 4-tuple 〈N, Σ, P, S〉, where:
- Σ is a set of terminal symbols (e.g., lexical items);
- N is a set of non-terminal symbols (the category labels);
- P is a set of productions of the form A → α, where
- A is a non-terminal, and
- α is a string of symbols from (N ∪ Σ)* (i.e., strings of either terminals or non-terminals);
- S is the start symbol.
A derivation of a string from a non-terminal A in grammar G is the result of successively applying productions from G to A. For example, (50) is a derivation of the dog with a telescope for the grammar in (37).
| (50) | NP Det N PP the N PP the dog PP the dog P NP the dog with NP the dog with Det N the dog with a N the dog with a telescope |
Although we have chosen here to expand the leftmost non-terminal symbol at each stage, this is not obligatory; productions can be applied in any order. Thus, derivation (50) could equally have started off in the following manner:
| (51) | NP Det N PP Det N P NP Det N with NP ... |
We can also write derivation (50) as:
| (52) | np ⇒ det n pp ⇒ the n pp ⇒ the dog pp ⇒ the dog p np ⇒ the dog with np ⇒ the dog with a n ⇒ the dog with a telescope |
where ⇒ means "derives in one step". We use ⇒* to mean "derives in zero or more steps":
- α ⇒* α for any string α, and
- if α ⇒* β and β ⇒ γ, then α ⇒* γ.
We write A ⇒* α to indicate that α can be derived from A.
In NLTK, context free grammars are defined in the parse.cfg module. The easiest way to construct a grammar object is from the standard string representation of grammars. In Listing 7.2 we define a grammar and use it to parse a simple sentence. You will learn more about parsing in the next section.
| ||
| ||
Listing 7.2 (cfg.py): Context Free Grammars in NLTK |
7.4.6 Exercises
☼ In the recursive descent parser demo, experiment with changing the sentence to be parsed by selecting Edit Text in the Edit menu.
☼ Can the grammar in (37) be used to describe sentences that are more than 20 words in length?
◑ You can modify the grammar in the recursive descent parser demo by selecting Edit Grammar in the Edit menu. Change the first expansion production, namely NP -> Det N PP, to NP -> NP PP. Using the Step button, try to build a parse tree. What happens?
◑ Extend the grammar in (40) with productions that expand prepositions as intransitive, transitive and requiring a pp complement. Based on these productions, use the method of the preceding exercise to draw a tree for the sentence Lee ran away home.
◑ Pick some common verbs and complete the following tasks:
- Write a program to find those verbs in the Prepositional Phrase Attachment Corpus nltk.corpus.ppattach. Find any cases where the same verb exhibits two different attachments, but where the first noun, or second noun, or preposition, stay unchanged (as we saw in Section (22)).
- Devise CFG grammar productions to cover some of these cases.
★ Write a function that takes a grammar (such as the one defined in Listing 7.2) and returns a random sentence generated by the grammar. (Use grammar.start() to find the start symbol of the grammar; grammar.productions(lhs) to get the list of productions from the grammar that have the specified left-hand side; and production.rhs() to get the right-hand side of a production.)
★ Lexical Acquisition: As we saw in Chapter 6, it is possible to collapse chunks down to their chunk label. When we do this for sentences involving the word gave, we find patterns such as the following:
gave NP gave up NP in NP gave NP up gave NP NP gave NP to NP
- Use this method to study the complementation patterns of a verb of interest, and write suitable grammar productions.
- Identify some English verbs that are near-synonyms, such as the dumped/filled/loaded example from earlier in this chapter. Use the chunking method to study the complementation patterns of these verbs. Create a grammar to cover these cases. Can the verbs be freely substituted for each other, or are their constraints? Discuss your findings.
7.5 Parsing
A parser processes input sentences according to the productions of a grammar, and builds one or more constituent structures that conform to the grammar. A grammar is a declarative specification of well-formedness. In NLTK, it is just a multi-line string; it is not itself a program that can be used for anything. A parser is a procedural interpretation of the grammar. It searches through the space of trees licensed by a grammar to find one that has the required sentence along its fringe.
Parsing is important in both linguistics and natural language processing. A parser permits a grammar to be evaluated against a potentially large collection of test sentences, helping linguists to find any problems in their grammatical analysis. A parser can serve as a model of psycholinguistic processing, helping to explain the difficulties that humans have with processing certain syntactic constructions. Many natural language applications involve parsing at some point; for example, we would expect the natural language questions submitted to a question-answering system to undergo parsing as an initial step.
In this section we see two simple parsing algorithms, a top-down method called recursive descent parsing, and a bottom-up method called shift-reduce parsing.
7.5.1 Recursive Descent Parsing
The simplest kind of parser interprets a grammar as a specification of how to break a high-level goal into several lower-level subgoals. The top-level goal is to find an s. The s → np vp production permits the parser to replace this goal with two subgoals: find an np, then find a vp. Each of these subgoals can be replaced in turn by sub-sub-goals, using productions that have np and vp on their left-hand side. Eventually, this expansion process leads to subgoals such as: find the word telescope. Such subgoals can be directly compared against the input string, and succeed if the next word is matched. If there is no match the parser must back up and try a different alternative.
The recursive descent parser builds a parse tree during the above process. With the initial goal (find an s), the s root node is created. As the above process recursively expands its goals using the productions of the grammar, the parse tree is extended downwards (hence the name recursive descent). We can see this in action using the parser demonstration nltk.draw.rdparser.demo(). Six stages of the execution of this parser are shown in Table 7.3.
|
|
|
|
|
|
During this process, the parser is often forced to choose between several possible productions. For example, in going from step 3 to step 4, it tries to find productions with n on the left-hand side. The first of these is n → man. When this does not work it backtracks, and tries other n productions in order, under it gets to n → dog, which matches the next word in the input sentence. Much later, as shown in step 5, it finds a complete parse. This is a tree that covers the entire sentence, without any dangling edges. Once a parse has been found, we can get the parser to look for additional parses. Again it will backtrack and explore other choices of production in case any of them result in a parse.
NLTK provides a recursive descent parser:
|
Note
RecursiveDescentParser() takes an optional parameter trace. If trace is greater than zero, then the parser will report the steps that it takes as it parses a text.
Recursive descent parsing has three key shortcomings. First, left-recursive productions like np → np pp send it into an infinite loop. Second, the parser wastes a lot of time considering words and structures that do not correspond to the input sentence. Third, the backtracking process may discard parsed constituents that will need to be rebuilt again later. For example, backtracking over vp → v np will discard the subtree created for the np. If the parser then proceeds with vp → v np pp, then the np subtree must be created all over again.
Recursive descent parsing is a kind of top-down parsing. Top-down parsers use a grammar to predict what the input will be, before inspecting the input! However, since the input is available to the parser all along, it would be more sensible to consider the input sentence from the very beginning. This approach is called bottom-up parsing, and we will see an example in the next section.
7.5.2 Shift-Reduce Parsing
A simple kind of bottom-up parser is the shift-reduce parser. In common with all bottom-up parsers, a shift-reduce parser tries to find sequences of words and phrases that correspond to the right hand side of a grammar production, and replace them with the left-hand side, until the whole sentence is reduced to an s.
The shift-reduce parser repeatedly pushes the next input word onto a stack (Section 5.2.4); this is the shift operation. If the top n items on the stack match the n items on the right hand side of some production, then they are all popped off the stack, and the item on the left-hand side of the production is pushed on the stack. This replacement of the top n items with a single item is the reduce operation. (This reduce operation may only be applied to the top of the stack; reducing items lower in the stack must be done before later items are pushed onto the stack.) The parser finishes when all the input is consumed and there is only one item remaining on the stack, a parse tree with an s node as its root.
The shift-reduce parser builds a parse tree during the above process. If the top of stack holds the word dog, and if the grammar has a production n → dog, then the reduce operation causes the word to be replaced with the parse tree for this production. For convenience we will represent this tree as N(dog). At a later stage, if the top of the stack holds two items Det(the) N(dog) and if the grammar has a production np → det n then the reduce operation causes these two items to be replaced with NP(Det(the), N(dog)). This process continues until a parse tree for the entire sentence has been constructed. We can see this in action using the parser demonstration nltk.draw.srparser.demo(). Six stages of the execution of this parser are shown in Figure 7.4.

|

|

|

|
|
|
NLTK provides ShiftReduceParser(), a simple implementation of a shift-reduce parser. This parser does not implement any backtracking, so it is not guaranteed to find a parse for a text, even if one exists. Furthermore, it will only find at most one parse, even if more parses exist. We can provide an optional trace parameter that controls how verbosely the parser reports the steps that it takes as it parses a text:
|
Shift-reduce parsers have a number of problems. A shift-reduce parser may fail to parse the sentence, even though the sentence is well-formed according to the grammar. In such cases, there are no remaining input words to shift, and there is no way to reduce the remaining items on the stack, as exemplified in Table 7.51. The parser entered this blind alley at an earlier stage shown in Table 7.52, when it reduced instead of shifted. This situation is called a shift-reduce conflict. At another possible stage of processing shown in Table 7.53, the parser must choose between two possible reductions, both matching the top items on the stack: vp → vp np pp or np → np pp. This situation is called a reduce-reduce conflict.
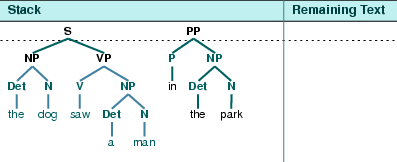
|
|
|
Shift-reduce parsers may implement policies for resolving such conflicts. For example, they may address shift-reduce conflicts by shifting only when no reductions are possible, and they may address reduce-reduce conflicts by favoring the reduction operation that removes the most items from the stack. No such policies are failsafe however.
The advantages of shift-reduce parsers over recursive descent parsers is that they only build structure that corresponds to the words in the input. Furthermore, they only build each sub-structure once, e.g. NP(Det(the), N(man)) is only built and pushed onto the stack a single time, regardless of whether it will later be used by the vp → v np pp reduction or the np → np pp reduction.
7.5.3 The Left-Corner Parser
One of the problems with the recursive descent parser is that it can get into an infinite loop. This is because it applies the grammar productions blindly, without considering the actual input sentence. A left-corner parser is a hybrid between the bottom-up and top-down approaches we have seen.
Grammar (40) allows us to produce the following parse of John saw Mary:
| (53) |  |
Recall that the grammar in (40) has the following productions for expanding np:
| (54) |
|
Suppose we ask you to first look at tree (53), and then decide which of the np productions you'd want a recursive descent parser to apply first — obviously, (54c) is the right choice! How do you know that it would be pointless to apply (54a) or (54b) instead? Because neither of these productions will derive a string whose first word is John. That is, we can easily tell that in a successful parse of John saw Mary, the parser has to expand np in such a way that np derives the string John α. More generally, we say that a category B is a left-corner of a tree rooted in A if A ⇒* B α.
| (55) |  |
A left-corner parser is a top-down parser with bottom-up filtering. Unlike an ordinary recursive descent parser, it does not get trapped in left recursive productions. Before starting its work, a left-corner parser preprocesses the context-free grammar to build a table where each row contains two cells, the first holding a non-terminal, and the second holding the collection of possible left corners of that non-terminal. Table 7.6 illustrates this for the grammar from (40).
| Category | Left-Corners (pre-terminals) |
|---|---|
| S | NP |
| NP | Det, PropN |
| VP | V |
| PP | P |
Each time a production is considered by the parser, it checks that the next input word is compatible with at least one of the pre-terminal categories in the left-corner table.
[TODO: explain how this effects the action of the parser, and why this solves the problem.]
7.5.4 Exercises
- ☼ With pen and paper, manually trace the execution of a recursive descent parser and a shift-reduce parser, for a CFG you have already seen, or one of your own devising.
- ◑ Compare the performance of the top-down, bottom-up, and left-corner parsers using the same grammar and three grammatical test sentences. Use timeit to log the amount of time each parser takes on the same sentence (Section 5.5.4). Write a function that runs all three parsers on all three sentences, and prints a 3-by-3 grid of times, as well as row and column totals. Discuss your findings.
- ◑ Read up on "garden path" sentences. How might the computational work of a parser relate to the difficulty humans have with processing these sentences? http://en.wikipedia.org/wiki/Garden_path_sentence
- ★ Left-corner parser: Develop a left-corner parser based on the recursive descent parser, and inheriting from ParseI. (Note, this exercise requires knowledge of Python classes, covered in Chapter 9.)
- ★ Extend NLTK's shift-reduce parser to incorporate backtracking, so that it is guaranteed to find all parses that exist (i.e. it is complete).
7.6 Conclusion
We began this chapter talking about confusing encounters with grammar at school. We just wrote what we wanted to say, and our work was handed back with red marks showing all our grammar mistakes. If this kind of "grammar" seems like secret knowledge, the linguistic approach we have taken in this chapter is quite the opposite: grammatical structures are made explicit as we build trees on top of sentences. We can write down the grammar productions, and parsers can build the trees automatically. This thoroughly objective approach is widely referred to as generative grammar.
Note that we have only considered "toy grammars," small grammars that illustrate the key aspects of parsing. But there is an obvious question as to whether the general approach can be scaled up to cover large corpora of natural languages. How hard would it be to construct such a set of productions by hand? In general, the answer is: very hard. Even if we allow ourselves to use various formal devices that give much more succinct representations of grammar productions (some of which will be discussed in Chapter 8), it is still extremely difficult to keep control of the complex interactions between the many productions required to cover the major constructions of a language. In other words, it is hard to modularize grammars so that one portion can be developed independently of the other parts. This in turn means that it is difficult to distribute the task of grammar writing across a team of linguists. Another difficulty is that as the grammar expands to cover a wider and wider range of constructions, there is a corresponding increase in the number of analyses which are admitted for any one sentence. In other words, ambiguity increases with coverage.
Despite these problems, there are a number of large collaborative projects that have achieved interesting and impressive results in developing rule-based grammars for several languages. Examples are the Lexical Functional Grammar (LFG) Pargram project (http://www2.parc.com/istl/groups/nltt/pargram/), the Head-Driven Phrase Structure Grammar (HPSG) LinGO Matrix framework (http://www.delph-in.net/matrix/), and the Lexicalized Tree Adjoining Grammar XTAG Project (http://www.cis.upenn.edu/~xtag/).
7.7 Summary (notes)
- Sentences have internal organization, or constituent structure, that can be represented using a tree; notable features of constituent structure are: recursion, heads, complements, modifiers
- A grammar is a compact characterization of a potentially infinite set of sentences; we say that a tree is well-formed according to a grammar, or that a grammar licenses a tree.
- Syntactic ambiguity arises when one sentence has more than one syntactic structure (e.g. prepositional phrase attachment ambiguity).
- A parser is a procedure for finding one or more trees corresponding to a grammatically well-formed sentence.
- A simple top-down parser is the recursive descent parser (summary, problems)
- A simple bottom-up parser is the shift-reduce parser (summary, problems)
- It is difficult to develop a broad-coverage grammar...
7.8 Further Reading
For more examples of parsing with NLTK, please see the guide at http://nltk.org/doc/guides/parse.html.
There are many introductory books on syntax. [O'Grady1989LI]_ is a general introduction to linguistics, while [Radford, 1988] provides a gentle introduction to transformational grammar, and can be recommended for its coverage of transformational approaches to unbounded dependency constructions.
[Burton-Roberts, 1997] is very practically oriented textbook on how to analyze constituency in English, with extensive exemplification and exercises. [Huddleston & Pullum, 2002] provides an up-to-date and comprehensive analysis of syntactic phenomena in English.
Chapter 12 of [Jurafsky & Martin, 2008] covers formal grammars of English; Sections 13.1-3 cover simple parsing algorithms and techniques for dealing with ambiguity; Chapter 16 covers the Chomsky hierarchy and the formal complexity of natural language.
- LALR(1)
- Marcus parser
- Lexical Functional Grammar (LFG)
- Head-Driven Phrase Structure Grammar (HPSG) LinGO Matrix framework
- Lexicalized Tree Adjoining Grammar XTAG Project
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
8 Chart Parsing and Probabilistic Parsing
8.1 Introduction
Chapter 7 started with an introduction to constituent structure in English, showing how words in a sentence group together in predictable ways. We showed how to describe this structure using syntactic tree diagrams, and observed that it is sometimes desirable to assign more than one such tree to a given string. In this case, we said that the string was structurally ambiguous; and example was old men and women.
Treebanks are language resources in which the syntactic structure of a corpus of sentences has been annotated, usually by hand. However, we would also like to be able to produce trees algorithmically. A context-free phrase structure grammar (CFG) is a formal model for describing whether a given string can be assigned a particular constituent structure. Given a set of syntactic categories, the CFG uses a set of productions to say how a phrase of some category A can be analyzed into a sequence of smaller parts α1 ... αn. But a grammar is a static description of a set of strings; it does not tell us what sequence of steps we need to take to build a constituent structure for a string. For this, we need to use a parsing algorithm. We presented two such algorithms: Top-Down Recursive Descent (7.5.1) and Bottom-Up Shift-Reduce (7.5.2). As we pointed out, both parsing approaches suffer from important shortcomings. The Recursive Descent parser cannot handle left-recursive productions (e.g., productions such as np → np pp), and blindly expands categories top-down without checking whether they are compatible with the input string. The Shift-Reduce parser is not guaranteed to find a valid parse for the input even if one exists, and builds substructure without checking whether it is globally consistent with the grammar. As we will describe further below, the Recursive Descent parser is also inefficient in its search for parses.
So, parsing builds trees over sentences, according to a phrase structure grammar. Now, all the examples we gave in Chapter 7 only involved toy grammars containing a handful of productions. What happens if we try to scale up this approach to deal with realistic corpora of language? Unfortunately, as the coverage of the grammar increases and the length of the input sentences grows, the number of parse trees grows rapidly. In fact, it grows at an astronomical rate.
Let's explore this issue with the help of a simple example. The word fish is both a noun and a verb. We can make up the sentence fish fish fish, meaning fish like to fish for other fish. (Try this with police if you prefer something more sensible.) Here is a toy grammar for the "fish" sentences.
|
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint
Now we can try parsing a longer sentence, fish fish fish fish fish, which amongst other things, means 'fish that other fish fish are in the habit of fishing fish themselves'. We use the NLTK chart parser, which is presented later on in this chapter. This sentence has two readings.
|
As the length of this sentence goes up (3, 5, 7, ...) we get the following numbers of parse trees: 1; 2; 5; 14; 42; 132; 429; 1,430; 4,862; 16,796; 58,786; 208,012; ... (These are the Catalan numbers, which we saw in an exercise in Section 5.5). The last of these is for a sentence of length 23, the average length of sentences in the WSJ section of Penn Treebank. For a sentence of length 50 there would be over 1012 parses, and this is only half the length of the Piglet sentence (Section (17)), which young children process effortlessly. No practical NLP system could construct all millions of trees for a sentence and choose the appropriate one in the context. It's clear that humans don't do this either!
Note that the problem is not with our choice of example. [Church & Patil, 1982] point out that the syntactic ambiguity of pp attachment in sentences like (56) also grows in proportion to the Catalan numbers.
| (56) | Put the block in the box on the table. |
So much for structural ambiguity; what about lexical ambiguity? As soon as we try to construct a broad-coverage grammar, we are forced to make lexical entries highly ambiguous for their part of speech. In a toy grammar, a is only a determiner, dog is only a noun, and runs is only a verb. However, in a broad-coverage grammar, a is also a noun (e.g. part a), dog is also a verb (meaning to follow closely), and runs is also a noun (e.g. ski runs). In fact, all words can be referred to by name: e.g. the verb 'ate' is spelled with three letters; in speech we do not need to supply quotation marks. Furthermore, it is possible to verb most nouns. Thus a parser for a broad-coverage grammar will be overwhelmed with ambiguity. Even complete gibberish will often have a reading, e.g. the a are of I. As [Klavans & Resnik}, 1996] has pointed out, this is not word salad but a grammatical noun phrase, in which are is a noun meaning a hundredth of a hectare (or 100 sq m), and a and I are nouns designating coordinates, as shown in Figure 8.1.
Figure 8.1: The a are of I
Even though this phrase is unlikely, it is still grammatical and a a broad-coverage parser should be able to construct a parse tree for it. Similarly, sentences that seem to be unambiguous, such as John saw Mary, turn out to have other readings we would not have anticipated (as Abney explains). This ambiguity is unavoidable, and leads to horrendous inefficiency in parsing seemingly innocuous sentences.
Let's look more closely at this issue of efficiency. The top-down recursive-descent parser presented in Chapter 7 can be very inefficient, since it often builds and discards the same sub-structure many times over. We see this in Figure 8.1, where a phrase the block is identified as a noun phrase several times, and where this information is discarded each time we backtrack.
Note
You should try the recursive-descent parser demo if you haven't already: nltk.draw.srparser.demo()
|
|
|
|
In this chapter, we will present two independent methods for dealing with ambiguity. The first is chart parsing, which uses the algorithmic technique of dynamic programming to derive the parses of an ambiguous sentence more efficiently. The second is probabilistic parsing, which allows us to rank the parses of an ambiguous sentence on the basis of evidence from corpora.
8.2 Chart Parsing
In the introduction to this chapter, we pointed out that the simple parsers discussed in Chapter 7 suffered from limitations in both completeness and efficiency. In order to remedy these, we will apply the algorithm design technique of dynamic programming to the parsing problem. As we saw in Section 5.5.3, dynamic programming stores intermediate results and re-uses them when appropriate, achieving significant efficiency gains. This technique can be applied to syntactic parsing, allowing us to store partial solutions to the parsing task and then look them up as necessary in order to efficiently arrive at a complete solution. This approach to parsing is known as chart parsing, and is the focus of this section.
8.2.1 Well-Formed Substring Tables
Let's start off by defining a simple grammar.
|
As you can see, this grammar allows the vp opened the box on the floor to be analyzed in two ways, depending on where the pp is attached.
| (57) |
|
Dynamic programming allows us to build the pp on the floor just once. The first time we build it we save it in a table, then we look it up when we need to use it as a subconstituent of either the object np or the higher vp. This table is known as a well-formed substring table (or WFST for short). We will show how to construct the WFST bottom-up so as to systematically record what syntactic constituents have been found.
Let's set our input to be the sentence the kids opened the box on the floor. It is helpful to think of the input as being indexed like a Python list. We have illustrated this in Figure 8.2.

Figure 8.2: Slice Points in the Input String
This allows us to say that, for instance, the word opened spans (2, 3) in the input. This is reminiscent of the slice notation:
|
In a WFST, we record the position of the words by filling in cells in a triangular matrix: the vertical axis will denote the start position of a substring, while the horizontal axis will denote the end position (thus opened will appear in the cell with coordinates (2, 3)). To simplify this presentation, we will assume each word has a unique lexical category, and we will store this (not the word) in the matrix. So cell (2, 3) will contain the entry v. More generally, if our input string is a1a2 ... an, and our grammar contains a production of the form A → ai, then we add A to the cell (i-1, i).
So, for every word in tokens, we can look up in our grammar what category it belongs to.
|
For our WFST, we create an (n-1) × (n-1) matrix as a list of lists in Python, and initialize it with the lexical categories of each token, in the init_wfst() function in Listing 8.1. We also define a utility function display() to pretty-print the WFST for us. As expected, there is a v in cell (2, 3).
| ||
| ||
Listing 8.1 (wfst.py): Acceptor Using Well-Formed Substring Table (based on CYK algorithm) |
Returning to our tabular representation, given that we have det in cell (0, 1), and n in cell (1, 2), what should we put into cell (0, 2)? In other words, what syntactic category derives the kids? We have already established that Det derives the and n derives kids, so we need to find a production of the form A → det n, that is, a production whose right hand side matches the categories in the cells we have already found. From the grammar, we know that we can enter np in cell (0,2).
More generally, we can enter A in (i, j) if there is a production A → B C, and we find nonterminal B in (i, k) and C in (k, j). Listing 8.1 uses this inference step to complete the WFST.
Note
To help us easily retrieve productions by their right hand sides, we create an index for the grammar. This is an example of a space-time trade-off: we do a reverse lookup on the grammar, instead of having to check through entire list of productions each time we want to look up via the right hand side.
We conclude that there is a parse for the whole input string once we have constructed an s node that covers the whole input, from position 0 to position 8; i.e., we can conclude that s ⇒* a1a2 ... an.
Notice that we have not used any built-in parsing functions here. We've implemented a complete, primitive chart parser from the ground up!
8.2.2 Charts
By setting trace to True when calling the function complete_wfst(), we get additional output.
|
For example, this says that since we found Det at wfst[0][1] and N at wfst[1][2], we can add NP to wfst[0][2]. The same information can be represented in a directed acyclic graph, as shown in Figure 8.2(a). This graph is usually called a chart. Figure 8.2(b) is the corresponding graph representation, where we add a new edge labeled np to cover the input from 0 to 2.
|
|
(Charts are more general than the WFSTs we have seen, since they can hold multiple hypotheses for a given span.)
A WFST is a data structure that can be used by a variety of parsing algorithms. The particular method for constructing a WFST that we have just seen and has some shortcomings. First, as you can see, the WFST is not itself a parse tree, so the technique is strictly speaking recognizing that a sentence is admitted by a grammar, rather than parsing it. Second, it requires every non-lexical grammar production to be binary (see Section 8.5.1). Although it is possible to convert an arbitrary CFG into this form, we would prefer to use an approach without such a requirement. Third, as a bottom-up approach it is potentially wasteful, being able to propose constituents in locations that would not be licensed by the grammar. Finally, the WFST did not represent the structural ambiguity in the sentence (i.e. the two verb phrase readings). The vp in cell (2,8) was actually entered twice, once for a v np reading, and once for a vp pp reading. In the next section we will address these issues.
8.2.3 Exercises
- ☼ Consider the sequence of words: Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo. This is a grammatically correct sentence, as explained at http://en.wikipedia.org/wiki/Buffalo_buffalo_Buffalo_buffalo_buffalo_buffalo_Buffalo_buffalo. Consider the tree diagram presented on this Wikipedia page, and write down a suitable grammar. Normalize case to lowercase, to simulate the problem that a listener has when hearing this sentence. Can you find other parses for this sentence? How does the number of parse trees grow as the sentence gets longer? (More examples of these sentences can be found at http://en.wikipedia.org/wiki/List_of_homophonous_phrases).
- ◑ Consider the algorithm in Listing 8.1. Can you explain why parsing context-free grammar is proportional to n3?
- ◑ Modify the functions init_wfst() and complete_wfst() so that the contents of each cell in the WFST is a set of non-terminal symbols rather than a single non-terminal.
- ★ Modify the functions init_wfst() and complete_wfst() so that when a non-terminal symbol is added to a cell in the WFST, it includes a record of the cells from which it was derived. Implement a function that will convert a WFST in this form to a parse tree.
8.3 Active Charts
One important aspect of the tabular approach to parsing can be seen more clearly if we look at the graph representation: given our grammar, there are two different ways to derive a top-level vp for the input, as shown in Table 8.3(a,b). In our graph representation, we simply combine the two sets of edges to yield Table 8.3(c).
|
|
|
However, given a WFST we cannot necessarily read off the justification for adding a particular edge. For example, in 8.3(b), [Edge: VP, 2:8] might owe its existence to a production vp → v np pp. Unlike phrase structure trees, a WFST does not encode a relation of immediate dominance. In order to make such information available, we can label edges not just with a non-terminal category, but with the whole production that justified the addition of the edge. This is illustrated in Figure 8.3.
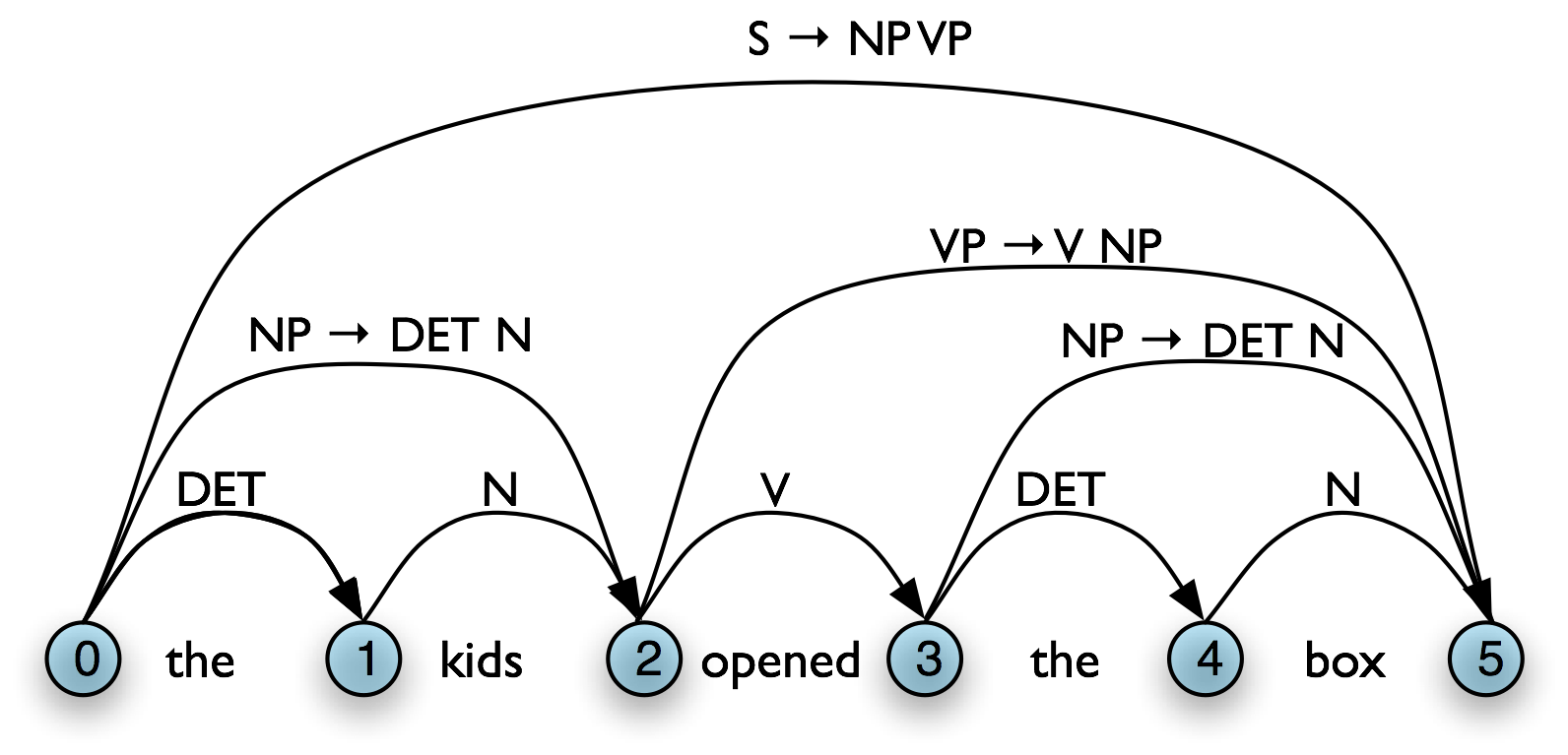
Figure 8.3: Chart Annotated with Productions
In general, a chart parser hypothesizes constituents (i.e. adds edges) based on the grammar, the tokens, and the constituents already found. Any constituent that is compatible with the current knowledge can be hypothesized; even though many of these hypothetical constituents will never be used in the final result. A WFST just records these hypotheses.
All of the edges that we've seen so far represent complete constituents. However, as we will see, it is helpful to hypothesize incomplete constituents. For example, the work done by a parser in processing the production VP → V NP PP can be reused when processing VP → V NP. Thus, we will record the hypothesis that "the v constituent likes is the beginning of a vp."
We can record such hypotheses by adding a dot to the edge's right hand side. Material to the left of the dot specifies what the constituent starts with; and material to the right of the dot specifies what still needs to be found in order to complete the constituent. For example, the edge in the Figure 8.4 records the hypothesis that "a vp starts with the v likes, but still needs an np to become complete":
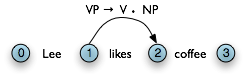
Figure 8.4: Chart Containing Incomplete VP Edge
These dotted edges are used to record all of the hypotheses that a chart parser makes about constituents in a sentence. Formally a dotted edge [A → c1 … cd • cd+1 … cn, (i, j)] records the hypothesis that a constituent of type A with span (i, j) starts with children c1 … cd, but still needs children cd+1 … cn to be complete (c1 … cd and cd+1 … cn may be empty). If d = n, then cd+1 … cn is empty and the edge represents a complete constituent and is called a complete edge. Otherwise, the edge represents an incomplete constituent, and is called an incomplete edge. In Figure 8.4(a), [vp → v np •, (1, 3)] is a complete edge, and [vp → v • np, (1, 2)] is an incomplete edge.
If d = 0, then c1 … cn is empty and the edge is called a self-loop edge. This is illustrated in Table 8.4(b). If a complete edge spans the entire sentence, and has the grammar's start symbol as its left-hand side, then the edge is called a parse edge, and it encodes one or more parse trees for the sentence. In Table 8.4(c), [s → np vp •, (0, 3)] is a parse edge.
a. Incomplete Edge
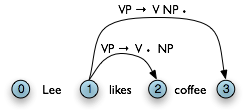 |
b. Self Loop Edge
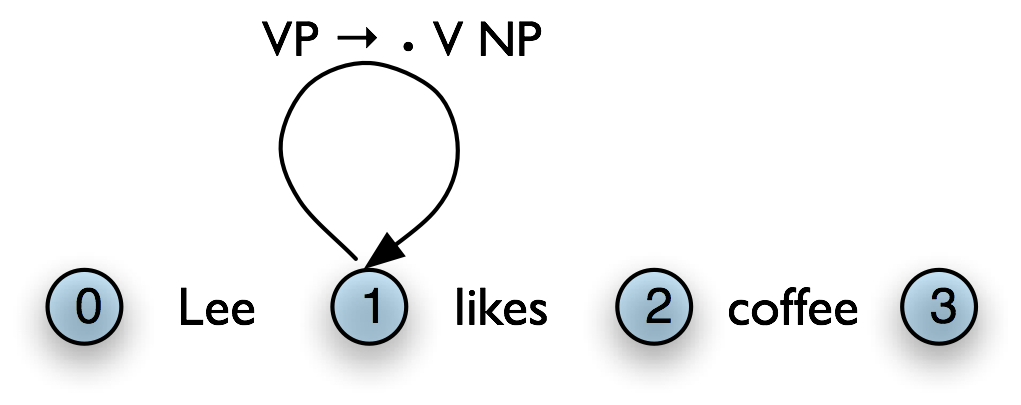 |
c. Parse Edge
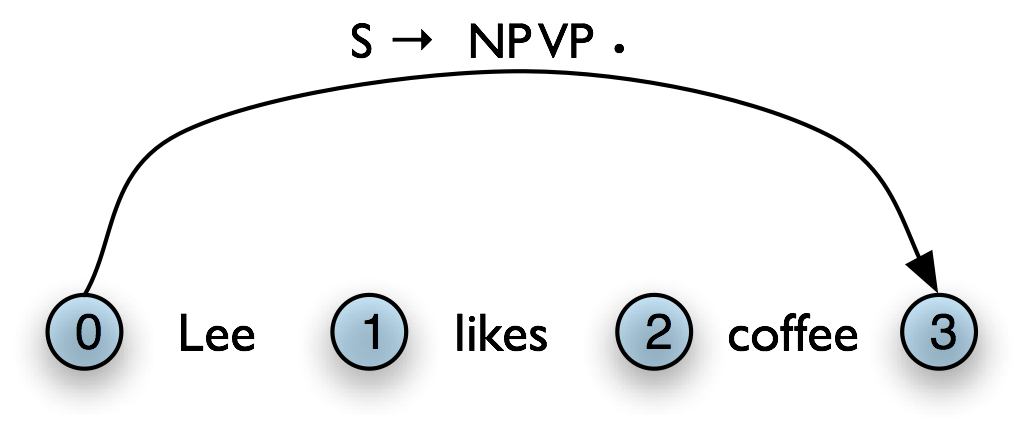 |
8.3.1 The Chart Parser
To parse a sentence, a chart parser first creates an empty chart spanning the sentence. It then finds edges that are licensed by its knowledge about the sentence, and adds them to the chart one at a time until one or more parse edges are found. The edges that it adds can be licensed in one of three ways:
- The input can license an edge. In particular, each word wi in the input licenses the complete edge [wi → •, (i, i+1)].
- The grammar can license an edge. In particular, each grammar production A → α licenses the self-loop edge [A → • α, (i, i)] for every i, 0 ≤ i < n.
- The current chart contents can license an edge.
However, it is not wise to add all licensed edges to the chart, since many of them will not be used in any complete parse. For example, even though the edge in the following chart is licensed (by the grammar), it will never be used in a complete parse:
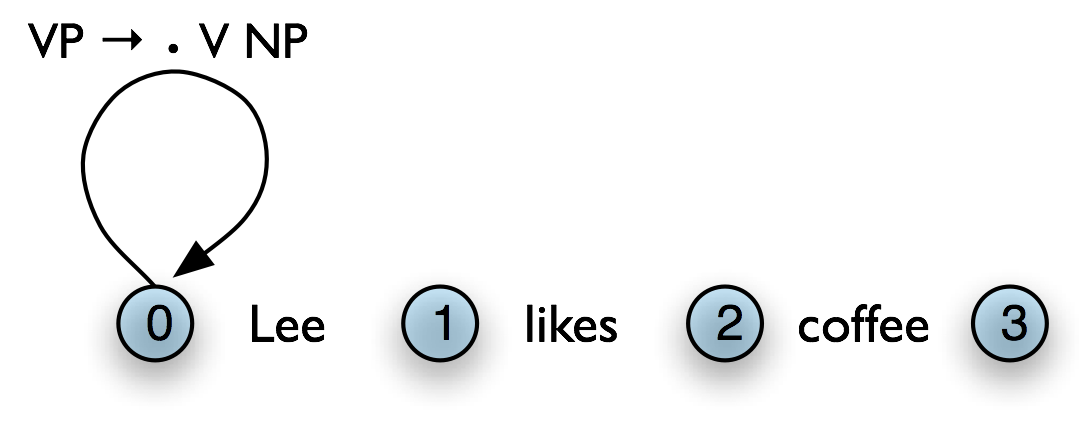
Figure 8.5: Chart Containing Redundant Edge
Chart parsers therefore use a set of rules to heuristically decide when an edge should be added to a chart. This set of rules, along with a specification of when they should be applied, forms a strategy.
8.3.2 The Fundamental Rule
One rule is particularly important, since it is used by every chart parser: the Fundamental Rule. This rule is used to combine an incomplete edge that's expecting a nonterminal B with a following, complete edge whose left hand side is B.
| (58) |
If the chart contains the edges [A → α • B β , (i, j)] [B → γ • , (j, k)] then add the new edge [A → α B • β , (i, k)] where α, β, and γ are (possibly empty) sequences of terminals or non-terminals |
Note that the dot has moved one place to the right, and the span of this new edge is the combined span of the other two. Note also that in adding this new edge we do not remove the other two, because they might be used again.
A somewhat more intuitive version of the operation of the Fundamental Rule can be given using chart diagrams. Thus, if we have a chart of the form shown in Table 8.5(a), then we can add a new complete edge as shown in Table 8.5(b).
a. Input
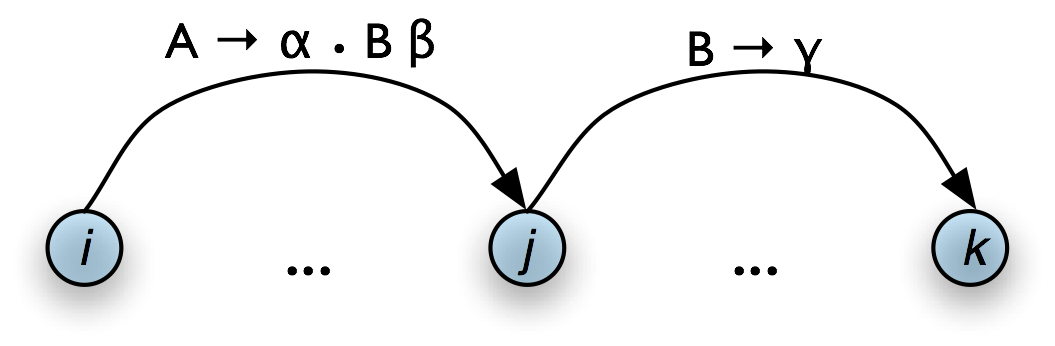 |
b. Output
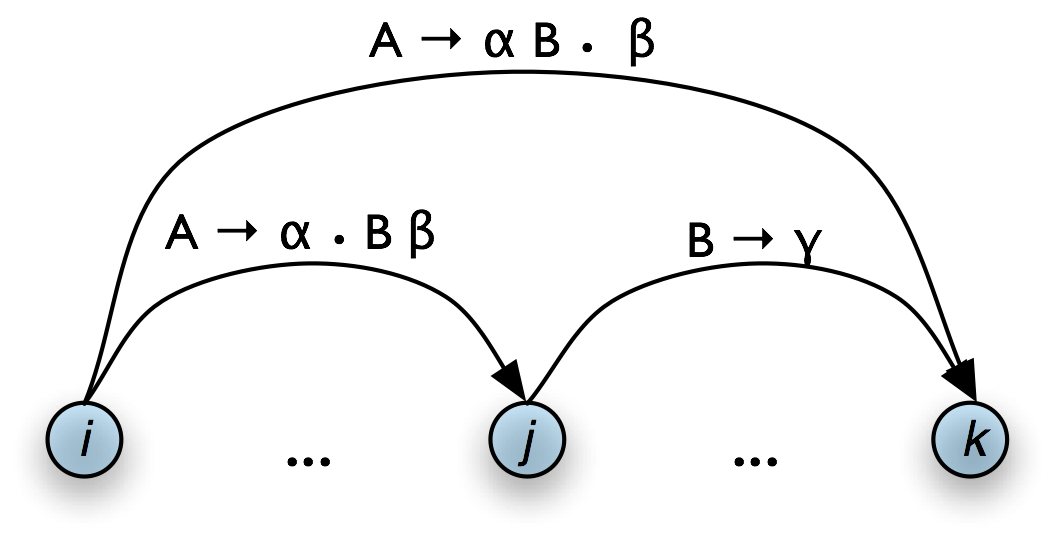 |
| [2] | The Fundamental Rule corresponds to the Completer function in the Earley algorithm; cf. [Jurafsky & Martin, 2008]. |
8.3.3 Bottom-Up Parsing
As we saw in Chapter 7, bottom-up parsing starts from the input string, and tries to find sequences of words and phrases that correspond to the right hand side of a grammar production. The parser then replaces these with the left-hand side of the production, until the whole sentence is reduced to an S. Bottom-up chart parsing is an extension of this approach in which hypotheses about structure are recorded as edges on a chart. In terms of our earlier terminology, bottom-up chart parsing can be seen as a parsing strategy; in other words, bottom-up is a particular choice of heuristics for adding new edges to a chart.
The general procedure for chart parsing is inductive: we start with a base case, and then show how we can move from a given state of the chart to a new state. Since we are working bottom-up, the base case for our induction will be determined by the words in the input string, so we add new edges for each word. Now, for the induction step, suppose the chart contains an edge labeled with constituent A. Since we are working bottom-up, we want to build constituents that can have an A as a daughter. In other words, we are going to look for productions of the form B → A β and use these to label new edges.
Let's look at the procedure a bit more formally. To create a bottom-up chart parser, we add to the Fundamental Rule two new rules: the Bottom-Up Initialization Rule; and the Bottom-Up Predict Rule. The Bottom-Up Initialization Rule says to add all edges licensed by the input.
| (59) |
For every word wi add the edge [wi → • , (i, i+1)] |
Table 8.6(a) illustrates this rule using the chart notation, while Table 8.6(b) shows the bottom-up initialization for the input Lee likes coffee.
a. Generic
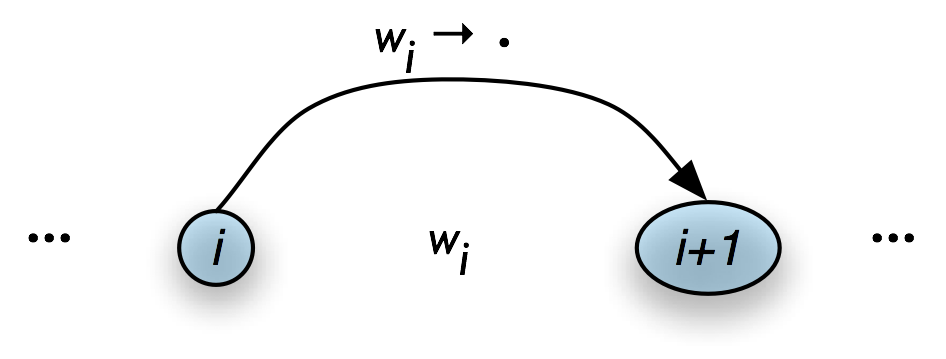 |
b. Example
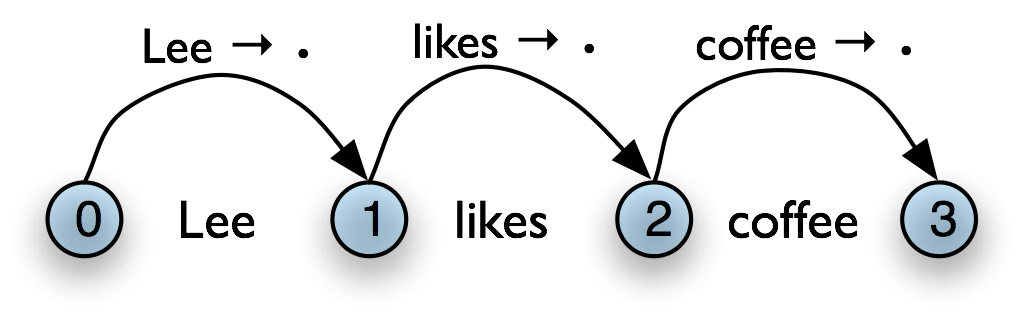 |
Notice that the dot on the right hand side of these productions is telling us that we have complete edges for the lexical items. By including this information, we can give a uniform statement of how the Fundamental Rule operates in Bottom-Up parsing, as we will shortly see.
Next, suppose the chart contains a complete edge e whose left hand category is A. Then the Bottom-Up Predict Rule requires the parser to add a self-loop edge at the left boundary of e for each grammar production whose right hand side begins with category A.
| (60) |
If the chart contains the complete edge [A → α • , (i, j)] and the grammar contains the production B → A β then add the self-loop edge [B → • A β , (i, i)] |
Graphically, if the chart looks as in Figure 8.7(a), then the Bottom-Up Predict Rule tells the parser to augment the chart as shown in Figure 8.7(b).
a. Input
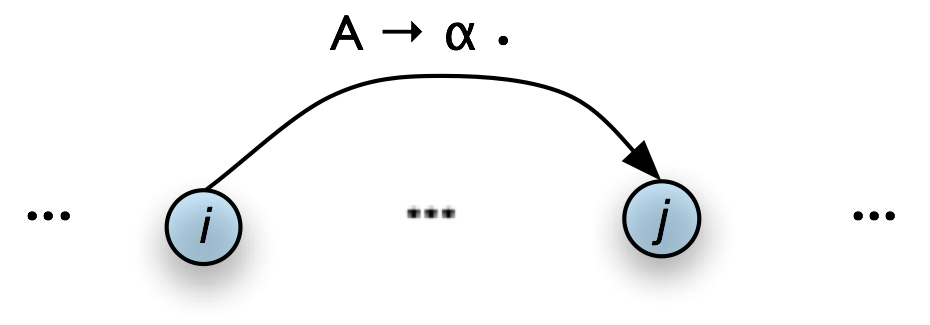 |
b. Output
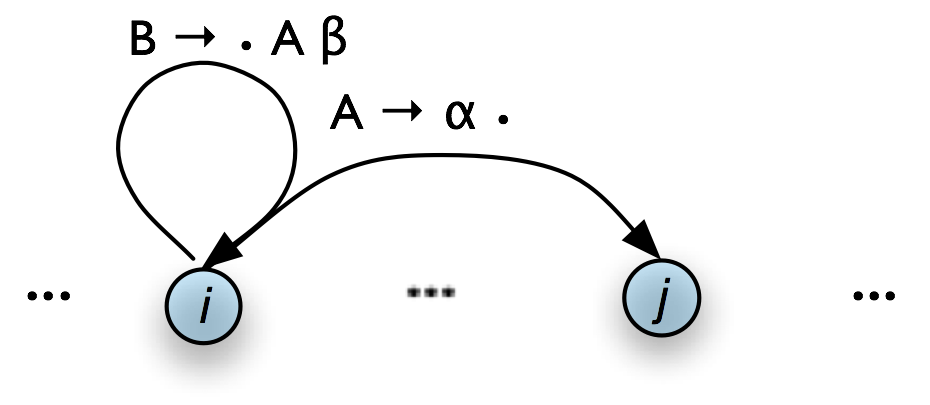 |
To continue our earlier example, let's suppose that our grammar contains the lexical productions shown in (61a). This allows us to add three self-loop edges to the chart, as shown in (61b).
| (61) |
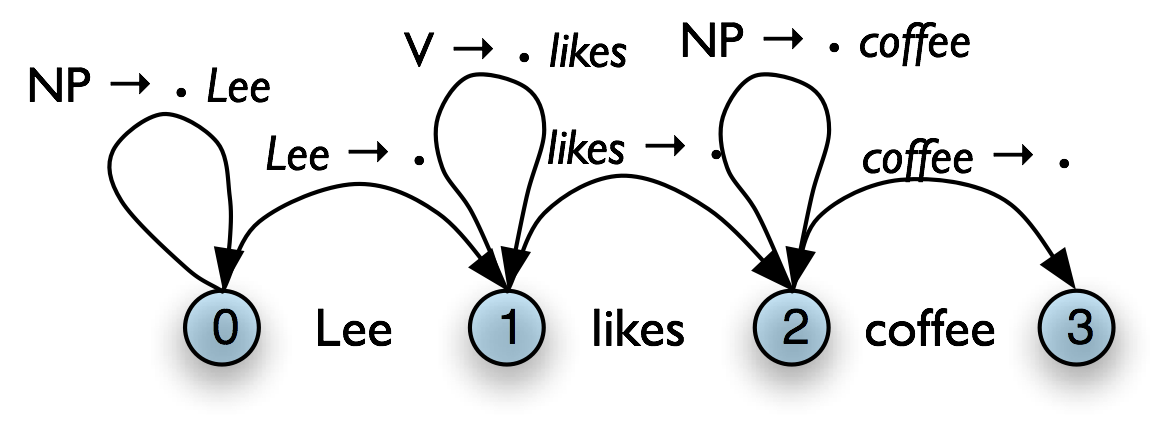 |
Once our chart contains an instance of the pattern shown in Figure 8.7(b), we can use the Fundamental Rule to add an edge where we have "moved the dot" one position to the right, as shown in Figure 8.8 (we have omitted the self-loop edges for simplicity.)
|
|
We will now be able to add new self-loop edges such as [s → • np vp, (0, 0)] and [vp → • vp np, (1, 1)], and use these to build more complete edges.
Using these three productions, we can parse a sentence as shown in (62).
| (62) |
Create an empty chart spanning the sentence. Apply the Bottom-Up Initialization Rule to each word. Until no more edges are added: Apply the Bottom-Up Predict Rule everywhere it applies. Apply the Fundamental Rule everywhere it applies. Return all of the parse trees corresponding to the parse edges in the chart. |
NLTK provides a useful interactive tool for visualizing the way in which charts are built, nltk.draw.chart.demo(). The tool comes with a pre-defined input string and grammar, but both of these can be readily modified with options inside the Edit menu. Figure 8.6 illustrates a window after the grammar has been updated:
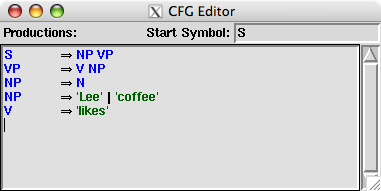
Figure 8.6: Modifying the demo() grammar
Note
To get the symbol ⇒ illustrated in Figure 8.6. you just have to type the keyboard characters '->'.
Figure 8.7 illustrates the tool interface. In order to invoke a rule, you simply click one of the green buttons at the bottom of the window. We show the state of the chart on the input Lee likes coffee after three applications of the Bottom-Up Initialization Rule, followed by successive applications of the Bottom-Up Predict Rule and the Fundamental Rule.
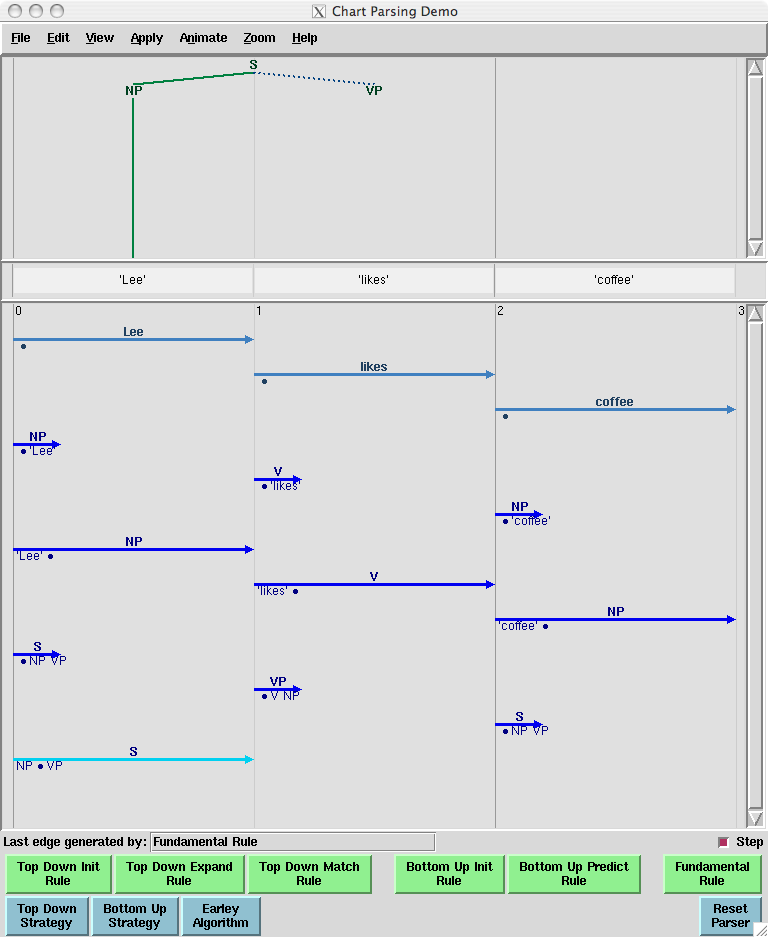
Figure 8.7: Incomplete chart for Lee likes coffee
Notice that in the topmost pane of the window, there is a partial tree showing that we have constructed an s with an np subject in the expectation that we will be able to find a vp.
8.3.4 Top-Down Parsing
Top-down chart parsing works in a similar way to the recursive descent parser discussed in Chapter 7, in that it starts off with the top-level goal of finding an s. This goal is then broken into the subgoals of trying to find constituents such as np and vp that can be immediately dominated by s. To create a top-down chart parser, we use the Fundamental Rule as before plus three other rules: the Top-Down Initialization Rule, the Top-Down Expand Rule, and the Top-Down Match Rule. The Top-Down Initialization Rule in (63) captures the fact that the root of any parse must be the start symbol s. It is illustrated graphically in Table 8.9.
| (63) |
For every grammar production of the form: s → α add the self-loop edge: [s → • α, (0, 0)] |
|
|
As we mentioned before, the dot on the right hand side of a production records how far our goals have been satisfied. So in Figure 8.9(b), we are predicting that we will be able to find an np and a vp, but have not yet satisfied these subgoals. So how do we pursue them? In order to find an np, for instance, we need to invoke a production that has np on its left hand side. The step of adding the required edge to the chart is accomplished with the Top-Down Expand Rule (64). This tells us that if our chart contains an incomplete edge whose dot is followed by a nonterminal B, then the parser should add any self-loop edges licensed by the grammar whose left-hand side is B.
| (64) |
If the chart contains the incomplete edge [A → α • B β , (i, j)] then for each grammar production B → γ add the edge [B → • γ , (j, j)] |
Thus, given a chart that looks like the one in Table 8.10(a), the Top-Down Expand Rule augments it with the edge shown in Table 8.10(b). In terms of our running example, we now have the chart shown in Table 8.10(c).
a. Input
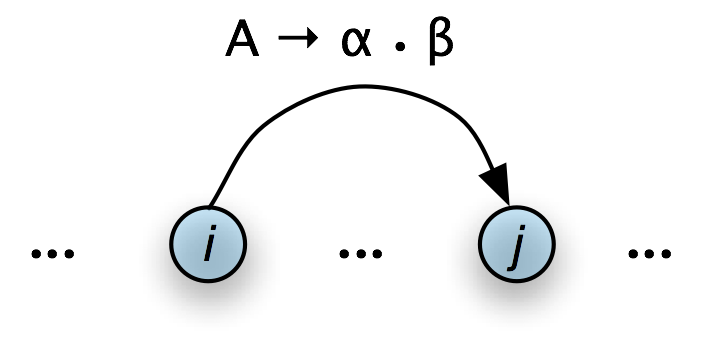 |
b. Output
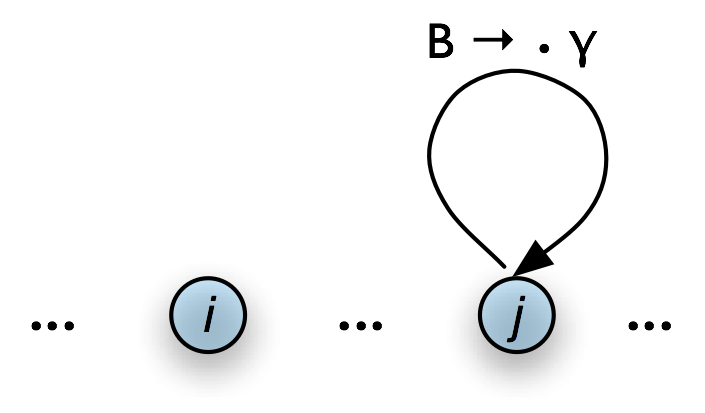 |
c. Example
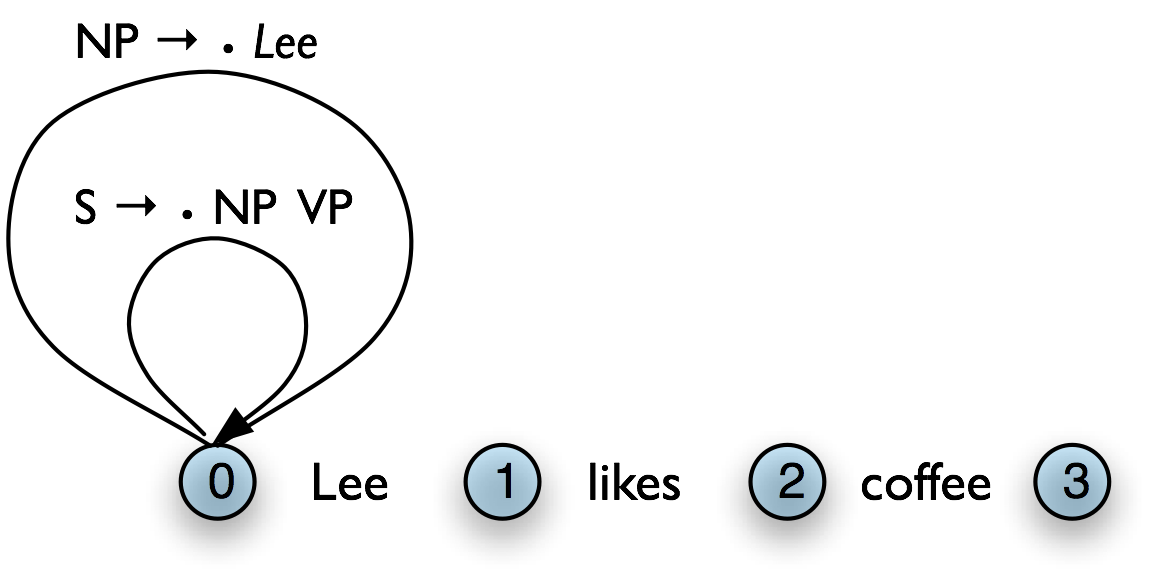 |
The Top-Down Match rule allows the predictions of the grammar to be matched against the input string. Thus, if the chart contains an incomplete edge whose dot is followed by a terminal w, then the parser should add an edge if the terminal corresponds to the current input symbol.
| (65) |
If the chart contains the incomplete edge [A → α • wj β, (i, j)], where wj is the j th word of the input, then add a new complete edge [wj → • , (j, j+1)] |
Graphically, the Top-Down Match rule takes us from Table 8.11(a), to Table 8.11(b).
a. Input
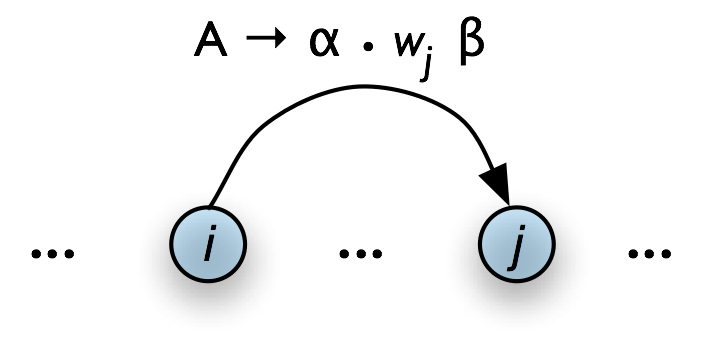 |
b. Output
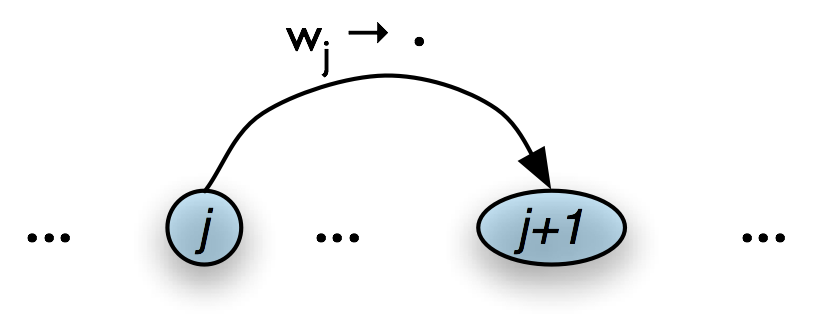 |
Figure 8.12(a) illustrates how our example chart after applying the Top-Down Match rule. What rule is relevant now? The Fundamental Rule. If we remove the self-loop edges from Figure 8.12(a) for simplicity, the Fundamental Rule gives us Figure 8.12(b).
a. Apply Top-Down Match Rule
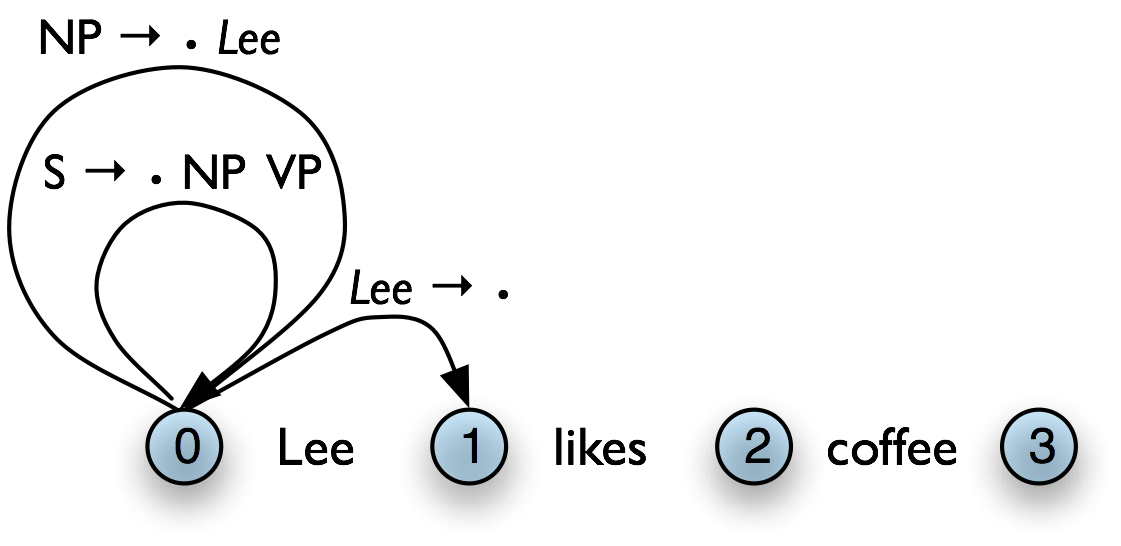 |
b. Apply Fundamental Rule
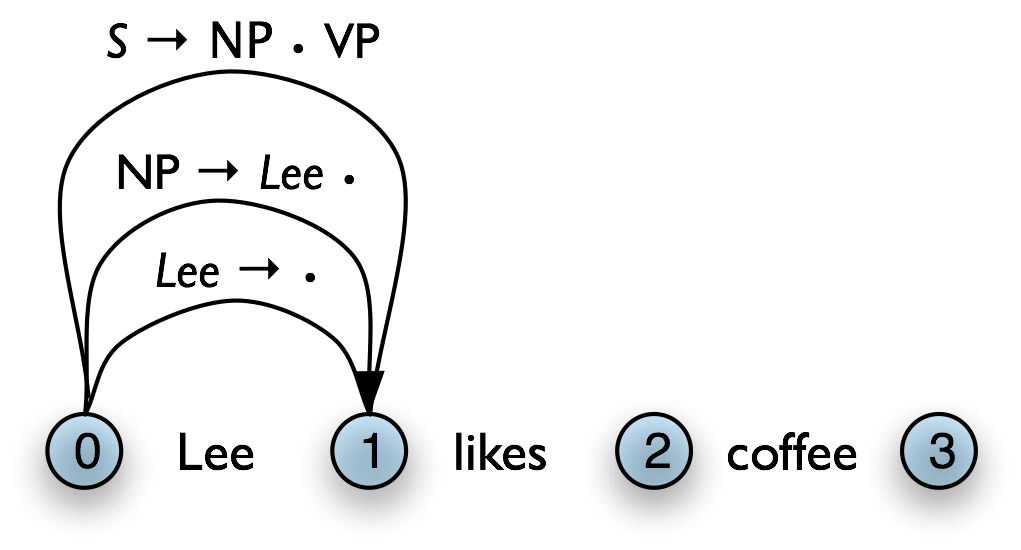 |
Using these four rules, we can parse a sentence top-down as shown in (66).
| (66) |
Create an empty chart spanning the sentence. Apply the Top-Down Initialization Rule. Until no more edges are added: Apply the Top-Down Expand Rule everywhere it applies. Apply the Top-Down Match Rule everywhere it applies. Apply the Fundamental Rule everywhere it applies. Return all of the parse trees corresponding to the parse edges in the chart. |
We encourage you to experiment with the NLTK chart parser demo, as before, in order to test out the top-down strategy yourself.
8.3.5 The Earley Algorithm
The Earley algorithm [Earley, 1970] is a parsing strategy that resembles the Top-Down Strategy, but deals more efficiently with matching against the input string. Table 8.13 shows the correspondence between the parsing rules introduced above and the rules used by the Earley algorithm.
| Top-Down/Bottom-Up | Earley |
|---|---|
| Top-Down Initialization Rule Top-Down Expand Rule | Predictor Rule |
| Top-Down/Bottom-Up Match Rule | Scanner Rule |
| Fundamental Rule | Completer Rule |
Let's look in more detail at the Scanner Rule. Suppose the chart contains an incomplete edge with a lexical category P immediately after the dot, the next word in the input is w, P is a part-of-speech label for w. Then the Scanner Rule admits a new complete edge in which P dominates w. More precisely:
| (67) |
If the chart contains the incomplete edge [A → α • P β, (i, j)] and wj is the jth word of the input, and P is a valid part of speech for wj, then add the new complete edges [P → wj •, (j, j+1)] [wj → •, (j, j+1)] |
To illustrate, suppose the input is of the form I saw ..., and the chart already contains the edge [vp → • v ..., (1, 1)]. Then the Scanner Rule will add to the chart the edges [v -> 'saw', (1, 2)] and ['saw'→ •, (1, 2)]. So in effect the Scanner Rule packages up a sequence of three rule applications: the Bottom-Up Initialization Rule for [w → •, (j, j+1)], the Top-Down Expand Rule for [P → • wj, (j, j)], and the Fundamental Rule for [P → wj •, (j, j+1))]. This is considerably more efficient than the Top-Down Strategy, that adds a new edge of the form [P → • w , (j, j)] for every lexical rule P → w, regardless of whether w can be found in the input. By contrast with Bottom-Up Initialization, however, the Earley algorithm proceeds strictly left-to-right through the input, applying all applicable rules at that point in the chart, and never backtracking. The NLTK chart parser demo, described above, allows the option of parsing according to the Earley algorithm.
8.3.6 Chart Parsing in NLTK
NLTK defines a simple yet flexible chart parser, ChartParser. A new chart parser is constructed from a grammar and a list of chart rules (also known as a strategy). These rules will be applied, in order, until no new edges are added to the chart. In particular, ChartParser uses the algorithm shown in (68).
| (68) |
Until no new edges are added:
For each chart rule R:
Apply R to any applicable edges in the chart.
Return any complete parses in the chart.
|
nltk.parse.chart defines two ready-made strategies: TD_STRATEGY, a basic top-down strategy; and BU_STRATEGY, a basic bottom-up strategy. When constructing a chart parser, you can use either of these strategies, or create your own.
The following example illustrates the use of the chart parser. We start by defining a simple grammar, and tokenizing a sentence. We make sure it is a list (not an iterator), since we wish to use the same tokenized sentence several times.
| ||
| ||
Listing 8.2 (chart_demo.py): Chart Parsing with NLTK |
The trace parameter can be specified when creating a parser, to turn on tracing (higher trace levels produce more verbose output). Example 8.3 shows the trace output for parsing a sentence with the bottom-up strategy. Notice that in this output, '[-----]' indicates a complete edge, '>' indicates a self-loop edge, and '[----->' indicates an incomplete edge.
| ||
Listing 8.3 (butrace.py): Trace of Bottom-Up Parser |
8.3.7 Exercises
- ☼ Use the graphical chart-parser interface to experiment with different rule invocation strategies. Come up with your own strategy that you can execute manually using the graphical interface. Describe the steps, and report any efficiency improvements it has (e.g. in terms of the size of the resulting chart). Do these improvements depend on the structure of the grammar? What do you think of the prospects for significant performance boosts from cleverer rule invocation strategies?
- ☼ We have seen that a chart parser adds but never removes edges from a chart. Why?
- ◑ Write a program to compare the efficiency of a top-down chart parser compared with a recursive descent parser (Section 7.5.1). Use the same grammar and input sentences for both. Compare their performance using the timeit module (Section 5.5.4).
8.4 Probabilistic Parsing
As we pointed out in the introduction to this chapter, dealing with ambiguity is a key challenge to broad coverage parsers. We have shown how chart parsing can help improve the efficiency of computing multiple parses of the same sentences. But the sheer number of parses can be just overwhelming. We will show how probabilistic parsing helps to manage a large space of parses. However, before we deal with these parsing issues, we must first back up and introduce weighted grammars.
8.4.1 Weighted Grammars
We begin by considering the verb give. This verb requires both a direct object (the thing being given) and an indirect object (the recipient). These complements can be given in either order, as illustrated in example (69b). In the "prepositional dative" form, the indirect object appears last, and inside a prepositional phrase, while in the "double object" form, the indirect object comes first:
| (69) |
|
Using the Penn Treebank sample, we can examine all instances of prepositional dative and double object constructions involving give, as shown in Listing 8.4.
| ||
| ||
Listing 8.4 (give.py): Usage of Give and Gave in the Penn Treebank sample |
We can observe a strong tendency for the shortest complement to appear first. However, this does not account for a form like give NP: federal judges / NP: a raise, where animacy may be playing a role. In fact there turn out to be a large number of contributing factors, as surveyed by [Bresnan & Hay, 2006].
How can such tendencies be expressed in a conventional context free grammar? It turns out that they cannot. However, we can address the problem by adding weights, or probabilities, to the productions of a grammar.
A probabilistic context free grammar (or PCFG) is a context free grammar that associates a probability with each of its productions. It generates the same set of parses for a text that the corresponding context free grammar does, and assigns a probability to each parse. The probability of a parse generated by a PCFG is simply the product of the probabilities of the productions used to generate it.
The simplest way to define a PCFG is to load it from a specially formatted string consisting of a sequence of weighted productions, where weights appear in brackets, as shown in Listing 8.5.
| ||
| ||
Listing 8.5 (pcfg1.py): Defining a Probabilistic Context Free Grammar (PCFG) |
It is sometimes convenient to combine multiple productions into a single line, e.g. VP -> TV NP [0.4] | IV [0.3] | DatV NP NP [0.3]. In order to ensure that the trees generated by the grammar form a probability distribution, PCFG grammars impose the constraint that all productions with a given left-hand side must have probabilities that sum to one. The grammar in Listing 8.5 obeys this constraint: for S, there is only one production, with a probability of 1.0; for VP, 0.4+0.3+0.3=1.0; and for NP, 0.8+0.2=1.0. The parse tree returned by parse() includes probabilities:
|
The next two sections introduce two probabilistic parsing algorithms for PCFGs. The first is an A* parser that uses Viterbi-style dynamic programming to find the single most likely parse for a given text. Whenever it finds multiple possible parses for a subtree, it discards all but the most likely parse. The second is a bottom-up chart parser that maintains a queue of edges, and adds them to the chart one at a time. The ordering of this queue is based on the probabilities associated with the edges, allowing the parser to expand more likely edges before less likely ones. Different queue orderings are used to implement a variety of different search strategies. These algorithms are implemented in the nltk.parse.viterbi and nltk.parse.pchart modules.
8.4.2 A* Parser
An A* Parser is a bottom-up PCFG parser that uses dynamic programming to find the single most likely parse for a text [Klein & Manning, 2003]. It parses texts by iteratively filling in a most likely constituents table. This table records the most likely tree for each span and node value. For example, after parsing the sentence "I saw the man with the telescope" with the grammar cfg.toy_pcfg1, the most likely constituents table contains the following entries (amongst others):
| Span | Node | Tree | Prob |
|---|---|---|---|
| [0:1] | NP | (NP I) | 0.15 |
| [6:7] | NP | (NN telescope) | 0.5 |
| [5:7] | NP | (NP the telescope) | 0.2 |
| [4:7] | PP | (PP with (NP the telescope)) | 0.122 |
| [0:4] | S | (S (NP I) (VP saw (NP the man))) | 0.01365 |
| [0:7] | S | (S (NP I) (VP saw (NP (NP the man) (PP with (NP the telescope))))) | 0.0004163250 |
Once the table has been completed, the parser returns the entry for the most likely constituent that spans the entire text, and whose node value is the start symbol. For this example, it would return the entry with a span of [0:6] and a node value of "S".
Note that we only record the most likely constituent for any given span and node value. For example, in the table above, there are actually two possible constituents that cover the span [1:6] and have "VP" node values.
- "saw the man, who has the telescope":
- (VP saw
- (NP (NP John)
- (PP with (NP the telescope))))
- "used the telescope to see the man":
- (VP saw
- (NP John) (PP with (NP the telescope)))
Since the grammar we are using to parse the text indicates that the first of these tree structures has a higher probability, the parser discards the second one.
Filling in the Most Likely Constituents Table: Because the grammar used by ViterbiParse is a PCFG, the probability of each constituent can be calculated from the probabilities of its children. Since a constituent's children can never cover a larger span than the constituent itself, each entry of the most likely constituents table depends only on entries for constituents with shorter spans (or equal spans, in the case of unary and epsilon productions).
ViterbiParse takes advantage of this fact, and fills in the most likely constituent table incrementally. It starts by filling in the entries for all constituents that span a single element of text. After it has filled in all the table entries for constituents that span one element of text, it fills in the entries for constituents that span two elements of text. It continues filling in the entries for constituents spanning larger and larger portions of the text, until the entire table has been filled.
To find the most likely constituent with a given span and node value, ViterbiParse considers all productions that could produce that node value. For each production, it checks the most likely constituents table for sequences of children that collectively cover the span and that have the node values specified by the production's right hand side. If the tree formed by applying the production to the children has a higher probability than the current table entry, then it updates the most likely constituents table with the new tree.
Handling Unary Productions and Epsilon Productions: A minor difficulty is introduced by unary productions and epsilon productions: an entry of the most likely constituents table might depend on another entry with the same span. For example, if the grammar contains the production V → VP, then the table entries for VP depend on the entries for V with the same span. This can be a problem if the constituents are checked in the wrong order. For example, if the parser tries to find the most likely constituent for a VP spanning [1:3] before it finds the most likely constituents for V spanning [1:3], then it can't apply the V → VP production.
To solve this problem, ViterbiParse repeatedly checks each span until it finds no new table entries. Note that cyclic grammar productions (e.g. V → V) will not cause this procedure to enter an infinite loop. Since all production probabilities are less than or equal to 1, any constituent generated by a cycle in the grammar will have a probability that is less than or equal to the original constituent; so ViterbiParse will discard it.
In NLTK, we create Viterbi parsers using ViterbiParse(). Note that since ViterbiParse only finds the single most likely parse, that nbest_parse() will never return more than one parse.
| ||
| ||
The trace method can be used to set the level of tracing output that is generated when parsing a text. Trace output displays the constituents that are considered, and indicates which ones are added to the most likely constituent table. It also indicates the likelihood for each constituent.
|
8.4.3 A Bottom-Up PCFG Chart Parser
The A* parser described in the previous section finds the single most likely parse for a given text. However, when parsers are used in the context of a larger NLP system, it is often necessary to produce several alternative parses. In the context of an overall system, a parse that is assigned low probability by the parser might still have the best overall probability.
For example, a probabilistic parser might decide that the most likely parse for "I saw John with the cookie" is is the structure with the interpretation "I used my cookie to see John"; but that parse would be assigned a low probability by a semantic system. Combining the probability estimates from the parser and the semantic system, the parse with the interpretation "I saw John, who had my cookie" would be given a higher overall probability.
This section describes a probabilistic bottom-up chart parser. It maintains an edge queue, and adds these edges to the chart one at a time. The ordering of this queue is based on the probabilities associated with the edges, and this allows the parser to insert the most probable edges first. Each time an edge is added to the chart, it may become possible to insert new edges, so these are added to the queue. The bottom-up chart parser continues adding the edges in the queue to the chart until enough complete parses have been found, or until the edge queue is empty.
Like an edge in a regular chart, a probabilistic edge consists of a dotted production, a span, and a (partial) parse tree. However, unlike ordinary charts, this time the tree is weighted with a probability. Its probability is the product of the probability of the production that generated it and the probabilities of its children. For example, the probability of the edge [Edge: S → NP • VP, 0:2] is the probability of the PCFG production S → NP VP multiplied by the probability of its np child. (Note that an edge's tree only includes children for elements to the left of the edge's dot. Thus, the edge's probability does not include probabilities for the constituents to the right of the edge's dot.)
8.4.4 Bottom-Up PCFG Strategies
The edge queue is a sorted list of edges that can be added to the chart. It is initialized with a single edge for each token in the text, with the form [Edge: token |rarr| |dot|]. As each edge from the queue is added to the chart, it may become possible to add further edges, according to two rules: (i) the Bottom-Up Initialization Rule can be used to add a self-loop edge whenever an edge whose dot is in position 0 is added to the chart; or (ii) the Fundamental Rule can be used to combine a new edge with edges already present in the chart. These additional edges are queued for addition to the chart.
By changing the sort order used by the queue, we can control the strategy that the parser uses to explore the search space. Since there are a wide variety of reasonable search strategies, BottomUpChartParser() does not define any sort order. Instead, different strategies are implemented in subclasses of BottomUpChartParser().
Lowest Cost First: The simplest way to order the edge queue is to sort edges by the probabilities of their associated trees (nltk.InsideChartParser()). This ordering concentrates the efforts of the parser on those edges that are more likely to be correct analyses of their underlying tokens.
The probability of an edge's tree provides an upper bound on the probability of any parse produced using that edge. The probabilistic "cost" of using an edge to form a parse is one minus its tree's probability. Thus, inserting the edges with the most likely trees first results in a lowest-cost-first search strategy. Lowest-cost-first search is optimal: the first solution it finds is guaranteed to be the best solution.
However, lowest-cost-first search can be rather inefficient. Recall that a tree's probability is the product of the probabilities of all the productions used to generate it. Consequently, smaller trees tend to have higher probabilities than larger ones. Thus, lowest-cost-first search tends to work with edges having small trees before considering edges with larger trees. Yet any complete parse of the text will necessarily have a large tree, and so this strategy will tend to produce complete parses only once most other edges are processed.
Let's consider this problem from another angle. The basic shortcoming with lowest-cost-first search is that it ignores the probability that an edge's tree will be part of a complete parse. The parser will try parses that are locally coherent even if they are unlikely to form part of a complete parse. Unfortunately, it can be quite difficult to calculate the probability that a tree is part of a complete parse. However, we can use a variety of techniques to approximate that probability.
Best-First Search: This method sorts the edge queue in descending order of the edges' span, no the assumption that edges having a larger span are more likely to form part of a complete parse. Thus, LongestParse employs a best-first search strategy, where it inserts the edges that are closest to producing complete parses before trying any other edges. Best-first search is not an optimal search strategy: the first solution it finds is not guaranteed to be the best solution. However, it will usually find a complete parse much more quickly than lowest-cost-first search.
Beam Search: When large grammars are used to parse a text, the edge queue can grow quite long. The edges at the end of a large well-sorted queue are unlikely to be used. Therefore, it is reasonable to remove (or prune) these edges from the queue. This strategy is known as beam search; it only keeps the best partial results. The bottom-up chart parsers take an optional parameter beam_size; whenever the edge queue grows longer than this, it is pruned. This parameter is best used in conjunction with InsideChartParser(). Beam search reduces the space requirements for lowest-cost-first search, by discarding edges that are not likely to be used. But beam search also loses many of lowest-cost-first search's more useful properties. Beam search is not optimal: it is not guaranteed to find the best parse first. In fact, since it might prune a necessary edge, beam search is not even complete: it is not guaranteed to return a parse if one exists.
In NLTK we can construct these parsers using InsideChartParser, LongestChartParser, RandomChartParser.
| ||
| ||
The trace method can be used to set the level of tracing output that is generated when parsing a text. Trace output displays edges as they are added to the chart, and shows the probability for each edges' tree.
|
8.5 Grammar Induction
As we have seen, PCFG productions are just like CFG productions, adorned with probabilities. So far, we have simply specified these probabilities in the grammar. However, it is more usual to estimate these probabilities from training data, namely a collection of parse trees or treebank.
The simplest method uses Maximum Likelihood Estimation, so called because probabilities are chosen in order to maximize the likelihood of the training data. The probability of a production VP → V NP PP is p(V,NP,PP | VP). We calculate this as follows:
count(VP -> V NP PP)
P(V,NP,PP | VP) = --------------------
count(VP -> ...)
Here is a simple program that induces a grammar from the first three parse trees in the Penn Treebank corpus:
|
8.5.1 Normal Forms
Grammar induction usually involves normalizing the grammar in various ways. NLTK trees support binarization (Chomsky Normal Form), parent annotation, Markov order-N smoothing, and unary collapsing:
|
These trees are shown in (70c).
| (70) |
|
8.7 Further Reading
Section 13.4 of [Jurafsky & Martin, 2008] covers chart parsing, and Chapter 14 contains a more formal presentation of statistical parsing.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
Introduction to Part III
Part III covers a selection of advanced topics. It begins with a chapter on applied programming in Python, covering topics in program development, standard libraries, and algorithm design. The following two chapters focus on making grammars more expressive, first by adding the powerful notation of distinctive features, and then by using this to add semantic interpretation. The final chapter deals with linguistic data management.
9 Applied Programming in Python
This chapter is in development.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
10 Feature Based Grammar
10.1 Introduction
Imagine you are building a spoken dialogue system to answer queries about train schedules in Europe. (71) illustrates one of the input sentences that the system should handle.
| (71) | Which stations does the 9.00 express from Amsterdam to Paris stop at? |
The information that the customer is seeking is not exotic — the system back-end just needs to look up the list of stations on the route, and reel them off. But you have to be careful in giving the correct semantic interpretation to (71). You don't want to end up with the system trying to answer (72) instead:
| (72) | Which station does the 9.00 express from Amsterdam terminate at? |
Part of your solution might use domain knowledge to figure out that if a speaker knows that the train is a train to Paris, then she probably isn't asking about the terminating station in (71). But the solution will also involve recognizing the syntactic structure of the speaker's query. In particular, your analyzer must recognize that there is a syntactic connection between the question phrase which stations, and the phrase stop at at the end (71). The required interpretation is made clearer in the "quiz question version shown in (73), where the question phrase fills the "gap" that is implicit in (71):
| (73) | The 9.00 express from Amsterdam to Paris stops at which stations? |
The long-distance dependency between an initial question phrase and the gap that it semantically connects to cannot be recognized by techniques we have presented in earlier chapters. For example, we can't use n-gram based language models; in practical terms, it is infeasible to observe the n-grams for a big enough value of n. Similarly, chunking grammars only attempt to capture local patterns, and therefore just don't "see" long-distance dependencies. In this chapter, we will show how syntactic features can be used to provide a simple yet effective technique for keeping track of long-distance dependencies in sentences.
Features are helpful too for dealing with purely local dependencies. Consider the German questions (74).
| (74) |
The only way of telling which noun phrase is the subject of kennen ('know') and which is the object is by looking at the agreement inflection on the verb — word order is no help to us here. Since verbs in German agree in number with their subjects, the plural form kennen requires Welche Studenten as subject, while the singular form kennt requires Franz as subject. The fact that subjects and verbs must agree in number can be expressed within the CFGs that we presented in Chapter 7. But capturing the fact that the interpretations of germanagra and germanagrb differ is more challenging. In this chapter, we will only examine the syntactic aspect of local dependencies such as number agreement. In Chapter 11, we will demonstrate how feature-based grammars can be extended so that they build a representation of meaning in parallel with a representation of syntactic structure.
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint
10.2 Why Features?
We have already used the term "feature" a few times, without saying what it means. What's special about feature-based grammars? The core ideas are probably already familiar to you. To make things concrete, let's look at the simple phrase these dogs. It's composed of two words. We'll be a bit abstract for the moment, and call these words a and b. We'll be modest, and assume that we do not know everything about them, but we can at least give a partial description. For example, we know that the orthography of a is these, its phonological form is DH IY Z, its part-of-speech is Det, and its number is plural. We can use dot notation to record these observations:
| (75) | a.spelling = these a.phonology = DH IY Z a.pos = Det a.number = plural |
Thus (75) is a partial description of a word; it lists some attributes, or features, of the word, and declares their values. There are other attributes that we might be interested in, which have not been specified; for example, what head the word is dependent on (using the notion of dependency discussed in Chapter 7), and what the lemma of the word is. But this omission of some attributes is exactly what you would expect from a partial description!
We will start off this chapter by looking more closely at the phenomenon of syntactic agreement; we will show how agreement constraints can be expressed elegantly using features, and illustrate their use in a simple grammar. Feature structures are a general data structure for representing information of any kind; we will briefly look at them from a more formal point of view, and explain how to create feature structures in Python. In the final part of the chapter, we demonstrate that the additional expressiveness of features opens out a wide spectrum of possibilities for describing sophisticated aspects of linguistic structure.
10.2.1 Syntactic Agreement
Consider the following contrasts:
| (76) |
|
| (77) |
|
In English, nouns are usually morphologically marked as being singular or plural. The form of the demonstrative also varies: this (singular) and these (plural). Examples (76b) and (77b) show that there are constraints on the use of demonstratives and nouns within a noun phrase: either both are singular or both are plural. A similar constraint holds between subjects and predicates:
| (78) |
|
| (79) |
|
Here we can see that morphological properties of the verb co-vary with syntactic properties of the subject noun phrase. This co-variance is called agreement. If we look further at verb agreement in English, we will see that present tense verbs typically have two inflected forms: one for third person singular, and another for every other combination of person and number:
| singular | plural | |
| 1st per | I run | we run |
| 2nd per | you run | you run |
| 3rd per | he/she/it runs | they run |
We can make the role of morphological properties a bit more explicit as illustrated in runs and run. These representations indicate that the verb agrees with its subject in person and number. (We use "3" as an abbreviation for 3rd person, "SG" for singular and "PL" for plural.)
Let's see what happens when we encode these agreement constraints in a context-free grammar. We will begin with the simple CFG in (80).
| (80) | s → np vp np → Det n vp → v Det → 'this' n → 'dog' v → 'runs' |
Example (80) allows us to generate the sentence this dog runs; however, what we really want to do is also generate these dogs run while blocking unwanted strings such as *this dogs run and *these dog runs. The most straightforward approach is to add new non-terminals and productions to the grammar:
| (81) | S_SG → NP_SG VP_SG S_PL → NP_PL VP_PL NP_SG → Det_SG N_SG NP_PL → Det_PL N_PL VP_SG → V_SG VP_PL → V_PL Det_SG → 'this' Det_PL → 'these' N_SG → 'dog' N_PL → 'dogs' V_SG → 'runs' V_PL → 'run' |
It should be clear that this grammar will do the required task, but only at the cost of duplicating our previous set of productions.
10.2.2 Using Attributes and Constraints
We spoke informally of linguistic categories having properties; for example, that a noun has the property of being plural. Let's make this explicit:
| (82) | N[num=pl] |
In (82), we have introduced some new notation which says that the category N has a feature called num (short for 'number') and that the value of this feature is pl (short for 'plural'). We can add similar annotations to other categories, and use them in lexical entries:
| (83) | Det[num=sg] → 'this' Det[num=pl] → 'these' N[num=sg] → 'dog' N[num=pl] → 'dogs' V[num=sg] → 'runs' V[num=pl] → 'run' |
Does this help at all? So far, it looks just like a slightly more verbose alternative to what was specified in (81). Things become more interesting when we allow variables over feature values, and use these to state constraints:
| (84) |
|
We are using "?n" as a variable over values of num; it can be instantiated either to sg or pl. Its scope is limited to individual productions. That is, within (84a), for example, ?n must be instantiated to the same constant value; we can read the production as saying that whatever value NP takes for the feature num, VP must take the same value.
In order to understand how these feature constraints work, it's helpful to think about how one would go about building a tree. Lexical productions will admit the following local trees (trees of depth one):
| (85) |
|
| (86) |
|
Now (84b) says that whatever the num values of N and Det are, they have to be the same. Consequently, (84b) will permit (85a) and (86a) to be combined into an NP as shown in (87a) and it will also allow (85b) and (86b) to be combined, as in (87b). By contrast, (88a) and (88b) are prohibited because the roots of their constituent local trees differ in their values for the num feature.
| (87) |
|
| (88) |
|
Production (84c) can be thought of as saying that the num value of the head verb has to be the same as the num value of the VP mother. Combined with (84a), we derive the consequence that if the num value of the subject head noun is pl, then so is the num value of the VP's head verb.
| (89) | 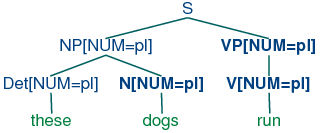 |
The grammar in listing 10.1 illustrates most of the ideas we have introduced so far in this chapter, plus a couple of new ones.
| ||
Listing 10.1 (feat0cfg.py): Example Feature-Based Grammar |
Notice that a syntactic category can have more than one feature; for example, v[tense=pres, num=pl]. In general, we can add as many features as we like.
Notice also that we have used feature variables in lexical entries as well as grammatical productions. For example, the has been assigned the category Det[num=?n]. Why is this? Well, you know that the definite article the can combine with both singular and plural nouns. One way of describing this would be to add two lexical entries to the grammar, one each for the singular and plural versions of the. However, a more elegant solution is to leave the num value underspecified and letting it agree in number with whatever noun it combines with.
A final detail about 10.1 is the statement %start S. This a "directive" that tells the parser to take s as the start symbol for the grammar.
In general, when we are trying to develop even a very small grammar, it is convenient to put the productions in a file where they can be edited, tested and revised. We have saved 10.1 as a file named 'feat0.fcfg' in the NLTK data distribution, and it can be accessed using nltk.data.load().
We can inspect the productions and the lexicon using the commands print g.earley_grammar() and pprint(g.earley_lexicon()).
Next, we can tokenize a sentence and use the nbest_parse() function to invoke the Earley chart parser.
| ||
Listing 10.2 (featurecharttrace.py): Trace of Feature-Based Chart Parser |
Observe that the parser works directly with the underspecified productions given by the grammar. That is, the Predictor rule does not attempt to compile out all admissible feature combinations before trying to expand the non-terminals on the left hand side of a production. However, when the Scanner matches an input word against a lexical production that has been predicted, the new edge will typically contain fully specified features; e.g., the edge [PropN[num = sg] → 'Kim', (0, 1)]. Recall from Chapter 7 that the Fundamental (or Completer) Rule in standard CFGs is used to combine an incomplete edge that's expecting a nonterminal B with a following, complete edge whose left hand side matches B. In our current setting, rather than checking for a complete match, we test whether the expected category B will unify with the left hand side B' of a following complete edge. We will explain in more detail in Section 10.3 how unification works; for the moment, it is enough to know that as a result of unification, any variable values of features in B will be instantiated by constant values in the corresponding feature structure in B', and these instantiated values will be used in the new edge added by the Completer. This instantiation can be seen, for example, in the edge [np[num=sg] → PropN[num=sg] •, (0, 1)] in 10.2, where the feature num has been assigned the value sg.
Finally, we can inspect the resulting parse trees (in this case, a single one).
|
10.2.3 Terminology
So far, we have only seen feature values like sg and pl. These simple values are usually called atomic — that is, they can't be decomposed into subparts. A special case of atomic values are boolean values, that is, values that just specify whether a property is true or false of a category. For example, we might want to distinguish auxiliary verbs such as can, may, will and do with the boolean feature aux. Then our lexicon for verbs could include entries such as (90). (Note that we follow the convention that boolean features are not written f +, f - but simply +f, -f, respectively.)
| (90) | V[tense=pres, +aux=+] → 'can' V[tense=pres, +aux=+] → 'may' V[tense=pres, -aux -] → 'walks' V[tense=pres, -aux -] → 'likes' |
We have spoken informally of attaching "feature annotations" to syntactic categories. A more general approach is to treat the whole category — that is, the non-terminal symbol plus the annotation — as a bundle of features. Consider, for example, the object we have written as (91).
| (91) | n[num=sg] |
The syntactic category n, as we have seen before, provides part of speech information. This information can itself be captured as a feature value pair, using pos to represent "part of speech":
| (92) | [pos=N, num=sg] |
In fact, we regard (92) as our "official" representation of a feature-based linguistic category, and (91) as a convenient abbreviation. A bundle of feature-value pairs is called a feature structure or an attribute value matrix (AVM). A feature structure that contains a specification for the feature pos is a linguistic category.
In addition to atomic-valued features, we allow features whose values are themselves feature structures. For example, we might want to group together agreement features (e.g., person, number and gender) as a distinguished part of a category, as shown in (93).
| (93) |
|
In this case, we say that the feature agr has a complex value.
There is no particular significance to the order of features in a feature structure. So (93) is equivalent to (93).
| (94) |
|
Once we have the possibility of using features like agr, we can refactor a grammar like 10.1 so that agreement features are bundled together. A tiny grammar illustrating this point is shown in (95).
| (95) | s → np[agr=?n] vp[agr=?n] np[agr=?n] → PropN[agr=?n] vp[tense=?t, agr=?n] → Cop[tense=?t, agr=?n] Adj Cop[tense=pres, agr=[num=sg, per=3]] → 'is' PropN[agr=[num=sg, per=3]] → 'Kim' Adj → 'happy' |
10.2.4 Exercises
☼ What constraints are required to correctly parse strings like I am happy and she is happy but not *you is happy or *they am happy? Implement two solutions for the present tense paradigm of the verb be in English, first taking Grammar (81) as your starting point, and then taking Grammar (95) as the starting point.
☼ Develop a variant of grammar 10.1 that uses a feature count to make the distinctions shown below:
(96) a. The boy sings.
b. *Boy sings.
(97) a. The boys sing.
b. Boys sing.
(98) a. The boys sing.
b. Boys sing.
(99) a. The water is precious.
b. Water is precious.
◑ Develop a feature-based grammar that will correctly describe the following Spanish noun phrases:
(100) un
cuadro
hermos-o
INDEF.SG.MASC
picture
beautiful-SG.MASC
'a beautiful picture'
(101) un-os
cuadro-s
hermos-os
INDEF-PL.MASC
picture-PL
beautiful-PL.MASC
'beautiful pictures'
(102) un-a
cortina
hermos-a
INDEF-SG.FEM
curtain
beautiful-SG.FEM
'a beautiful curtain'
(103) un-as
cortina-s
hermos-as
INDEF-PL.FEM
curtain
beautiful-PL.FEM
'beautiful curtains'
◑ Develop a wrapper for the earley_parser so that a trace is only printed if the input string fails to parse.
10.3 Computing with Feature Structures
In this section, we will show how feature structures can be constructed and manipulated in Python. We will also discuss the fundamental operation of unification, which allows us to combine the information contained in two different feature structures.
10.3.1 Feature Structures in Python
Feature structures are declared with the FeatStruct() constructor. Atomic feature values can be strings or integers.
|
A feature structure is actually just a kind of dictionary, and so we access its values by indexing in the usual way. We can use our familiar syntax to assign values to features:
|
We can also define feature structures that have complex values, as discussed earlier.
|
An alternative method of specifying feature structures is to use a bracketed string consisting of feature-value pairs in the format feature=value, where values may themselves be feature structures:
|
10.3.2 Feature Structures as Graphs
Feature structures are not inherently tied to linguistic objects; they are general purpose structures for representing knowledge. For example, we could encode information about a person in a feature structure:
|
| (104) |
|
It is sometimes helpful to view feature structures as graphs; more specifically, directed acyclic graphs (DAGs). (105) is equivalent to the AVM (104).
| (105) | 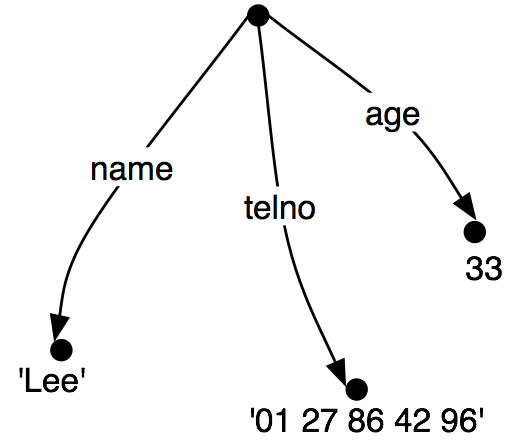 |
The feature names appear as labels on the directed arcs, and feature values appear as labels on the nodes that are pointed to by the arcs.
Just as before, feature values can be complex:
| (106) | 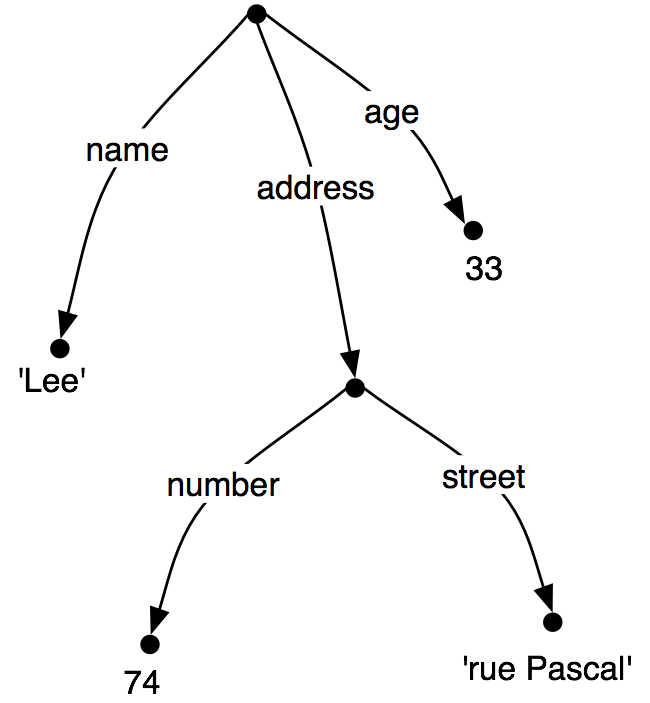 |
When we look at such graphs, it is natural to think in terms of paths through the graph. A feature path is a sequence of arcs that can be followed from the root node. We will represent paths as tuples. Thus, ('address', 'street') is a feature path whose value in (106) is the string "rue Pascal".
Now let's consider a situation where Lee has a spouse named "Kim", and Kim's address is the same as Lee's. We might represent this as (107).
| (107) | 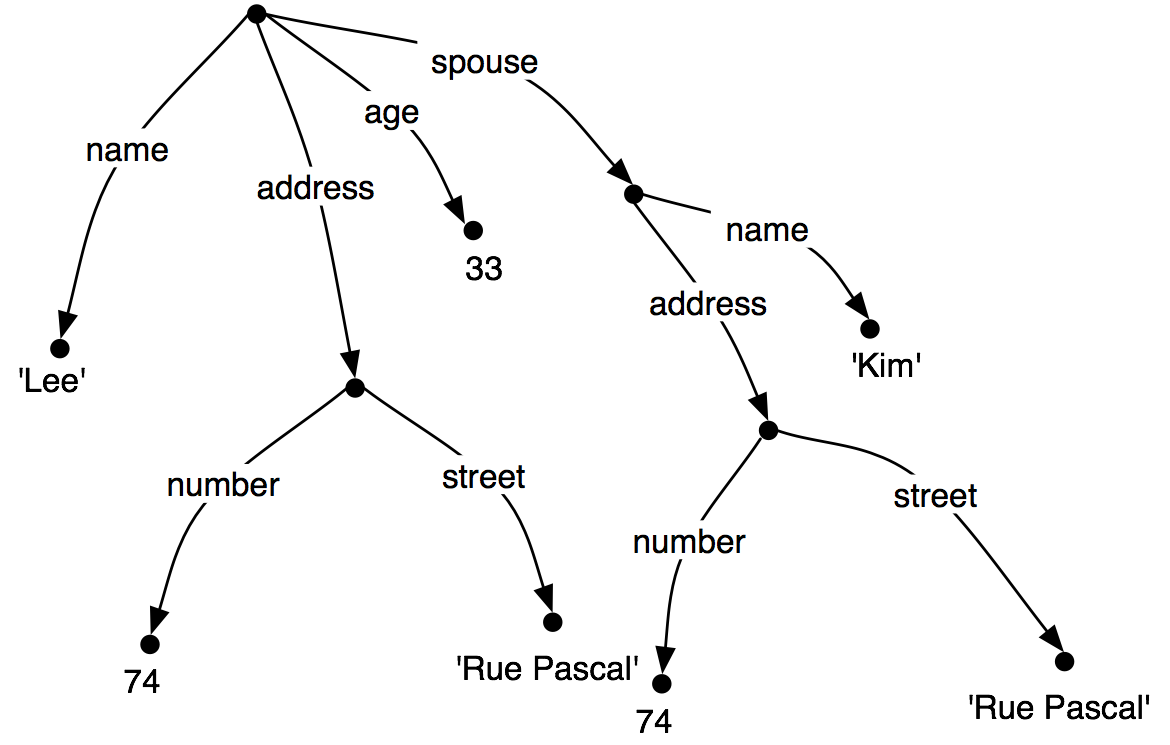 |
However, rather than repeating the address information in the feature structure, we can "share" the same sub-graph between different arcs:
| (108) | 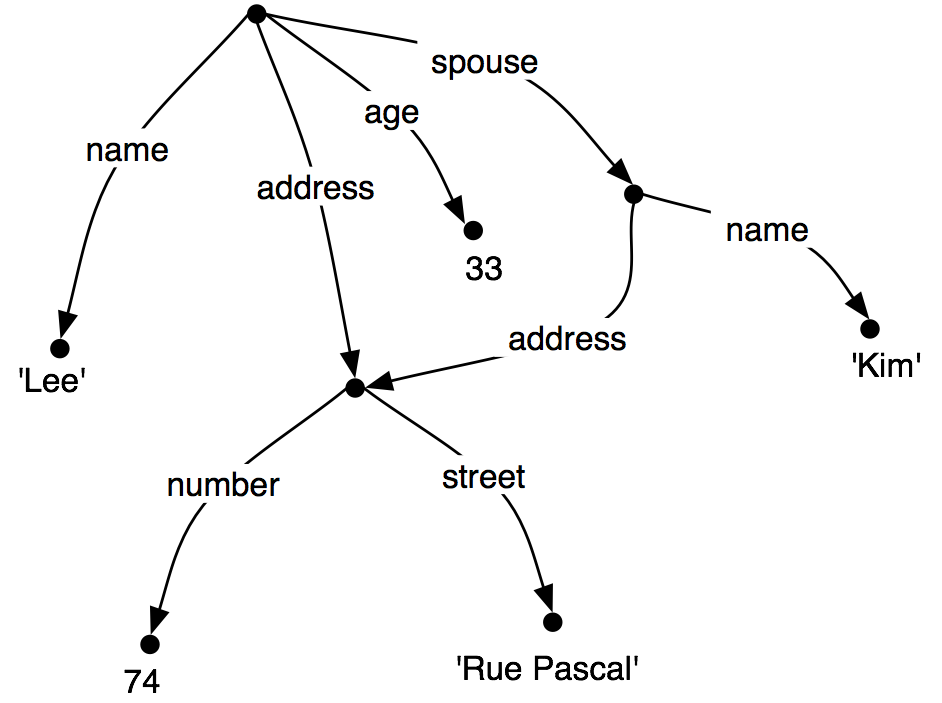 |
In other words, the value of the path ('ADDRESS') in (108) is identical to the value of the path ('SPOUSE', 'ADDRESS'). DAGs such as (108) are said to involve structure sharing or reentrancy. When two paths have the same value, they are said to be equivalent.
There are a number of notations for representing reentrancy in matrix-style representations of feature structures. We adopt the following convention: the first occurrence of a shared feature structure is prefixed with an integer in parentheses, such as (1), and any subsequent reference to that structure uses the notation ->(1), as shown below.
|
This is similar to more conventional displays of AVMs, as shown in (109).
| (109) |
|
The bracketed integer is sometimes called a tag or a coindex. The choice of integer is not significant. There can be any number of tags within a single feature structure.
|
| (110) |
|
10.3.3 Subsumption and Unification
It is standard to think of feature structures as providing partial information about some object, in the sense that we can order feature structures according to how general they are. For example, (111a) is more general (less specific) than (111b), which in turn is more general than (111c).
| (111) |
|
This ordering is called subsumption; a more general feature structure subsumes a less general one. If FS0 subsumes FS1 (formally, we write FS0 ⊑ FS1), then FS1 must have all the paths and path equivalences of FS0, and may have additional paths and equivalences as well. Thus, (107) subsumes (108), since the latter has additional path equivalences.. It should be obvious that subsumption only provides a partial ordering on feature structures, since some feature structures are incommensurable. For example, (112) neither subsumes nor is subsumed by (111a).
| (112) |
|
So we have seen that some feature structures are more specific than others. How do we go about specializing a given feature structure? For example, we might decide that addresses should consist of not just a street number and a street name, but also a city. That is, we might want to merge graph (113b) with (113a) to yield (113c).
| (113) |
|
Merging information from two feature structures is called unification and is supported by the unify() method.
|
Unification is formally defined as a binary operation: FS0 ⊓ FS1. Unification is symmetric, so
| (114) | FS0 ⊓ FS1 = FS1 ⊓ FS0. |
The same is true in Python:
|
If we unify two feature structures which stand in the subsumption relationship, then the result of unification is the most specific of the two:
| (115) | If FS0 ⊑ FS1, then FS0 ⊓ FS1 = FS1 |
For example, the result of unifying (111b) with (111c) is (111c).
Unification between FS0 and FS1 will fail if the two feature structures share a path π, but the value of π in FS0 is a distinct atom from the value of π in FS1. This is implemented by setting the result of unification to be None.
|
Now, if we look at how unification interacts with structure-sharing, things become really interesting. First, let's define (107) in Python:
|
| (116) |
|
What happens when we augment Kim's address with a specification for city? (Notice that fs1 includes the whole path from the root of the feature structure down to city.)
|
(117) shows the result of unifying fs0 with fs1:
| (117) |
|
By contrast, the result is very different if fs1 is unified with the structure-sharing version fs2 (also shown as (108)):
|
| (118) |
|
Rather than just updating what was in effect Kim's "copy" of Lee's address, we have now updated both their addresses at the same time. More generally, if a unification involves specializing the value of some path π, then that unification simultaneously specializes the value of any path that is equivalent to π.
As we have already seen, structure sharing can also be stated using variables such as ?x.
|
10.3.4 Exercises
☼ Write a function subsumes() which holds of two feature structures fs1 and fs2 just in case fs1 subsumes fs2.
◑ Consider the feature structures shown in Listing 10.3.
[XX] NOTE: This example is somewhat broken -- nltk doesn't support reentrance for base feature values. (See email ~7/23/08 to the nltk-users mailing list for details.)
fs1 = nltk.FeatStruct("[A = (1)b, B= [C ->(1)]]") fs2 = nltk.FeatStruct("[B = [D = d]]") fs3 = nltk.FeatStruct("[B = [C = d]]") fs4 = nltk.FeatStruct("[A = (1)[B = b], C->(1)]") fs5 = nltk.FeatStruct("[A = [D = (1)e], C = [E -> (1)] ]") fs6 = nltk.FeatStruct("[A = [D = (1)e], C = [B -> (1)] ]") fs7 = nltk.FeatStruct("[A = [D = (1)e, F = (2)[]], C = [B -> (1), E -> (2)] ]") fs8 = nltk.FeatStruct("[A = [B = b], C = [E = [G = e]]]") fs9 = nltk.FeatStruct("[A = (1)[B = b], C -> (1)]")
Work out on paper what the result is of the following unifications. (Hint: you might find it useful to draw the graph structures.)
- fs1 and fs2
- fs1 and fs3
- fs4 and fs5
- fs5 and fs6
- fs7 and fs8
- fs7 and fs9
Check your answers using Python.
◑ List two feature structures that subsume [A=?x, B=?x].
◑ Ignoring structure sharing, give an informal algorithm for unifying two feature structures.
10.4 Extending a Feature-Based Grammar
10.4.1 Subcategorization
In Chapter 7, we proposed to augment our category labels to represent different kinds of verb. We introduced labels such as iv and tv for intransitive and transitive verbs respectively. This allowed us to write productions like the following:
| (119) | vp → iv vp → tv np |
Although we know that iv and tv are two kinds of v, from a formal point of view iv has no closer relationship with tv than it does with np. As it stands, iv and tv are just atomic nonterminal symbols from a CFG. This approach doesn't allow us to say anything about the class of verbs in general. For example, we cannot say something like "All lexical items of category v can be marked for tense", since bark, say, is an item of category iv, not v. A simple solution, originally developed for a grammar framework called Generalized Phrase Structure Grammar (GPSG), stipulates that lexical categories may bear a subcat feature whose values are integers. This is illustrated in a modified portion of 10.1, shown in (120).
| (120) | VP[TENSE=?t, NUM=?n] -> V[SUBCAT=0, TENSE=?t, NUM=?n] VP[TENSE=?t, NUM=?n] -> V[SUBCAT=1, TENSE=?t, NUM=?n] NP VP[TENSE=?t, NUM=?n] -> V[SUBCAT=2, TENSE=?t, NUM=?n] Sbar V[SUBCAT=0, TENSE=pres, NUM=sg] -> 'disappears' | 'walks' V[SUBCAT=1, TENSE=pres, NUM=sg] -> 'sees' | 'likes' V[SUBCAT=2, TENSE=pres, NUM=sg] -> 'says' | 'claims' V[SUBCAT=0, TENSE=pres, NUM=pl] -> 'disappear' | 'walk' V[SUBCAT=1, TENSE=pres, NUM=pl] -> 'see' | 'like' V[SUBCAT=2, TENSE=pres, NUM=pl] -> 'say' | 'claim' V[SUBCAT=0, TENSE=past, NUM=?n] -> 'disappeared' | 'walked' V[SUBCAT=1, TENSE=past, NUM=?n] -> 'saw' | 'liked' V[SUBCAT=2, TENSE=past, NUM=?n] -> 'said' | 'claimed' |
When we see a lexical category like v[subcat 1], we can interpret the subcat specification as a pointer to the production in which v[subcat 1] is introduced as the head daughter in a vp production. By convention, there is a one-to-one correspondence between subcat values and the productions that introduce lexical heads. It's worth noting that the choice of integer which acts as a value for subcat is completely arbitrary — we could equally well have chosen 3999, 113 and 57 as our two values in (120). On this approach, subcat can only appear on lexical categories; it makes no sense, for example, to specify a subcat value on vp.
In our third class of verbs above, we have specified a category s-bar. This is a label for subordinate clauses such as the complement of claim in the example You claim that you like children. We require two further productions to analyze such sentences:
| (121) | S-BAR -> Comp S Comp -> 'that' |
The resulting structure is the following.
| (122) | 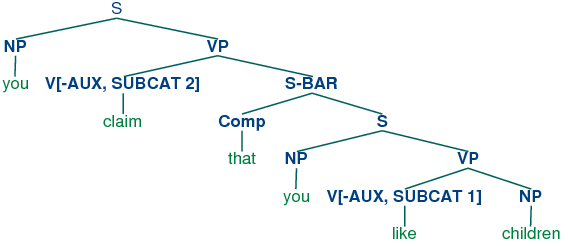 |
An alternative treatment of subcategorization, due originally to a framework known as categorial grammar, is represented in feature-based frameworks such as PATR and Head-driven Phrase Structure Grammar. Rather than using subcat values as a way of indexing productions, the subcat value directly encodes the valency of a head (the list of arguments that it can combine with). For example, a verb like put that takes np and pp complements (put the book on the table) might be represented as (123):
| (123) | v[subcat 〈np, np, pp〉 ] |
This says that the verb can combine with three arguments. The leftmost element in the list is the subject np, while everything else — an np followed by a pp in this case — comprises the subcategorized-for complements. When a verb like put is combined with appropriate complements, the requirements which are specified in the subcat are discharged, and only a subject np is needed. This category, which corresponds to what is traditionally thought of as vp, might be represented as follows.
| (124) | v[subcat 〈np〉 ] |
Finally, a sentence is a kind of verbal category that has no requirements for further arguments, and hence has a subcat whose value is the empty list. The tree (125) shows how these category assignments combine in a parse of Kim put the book on the table.
| (125) | 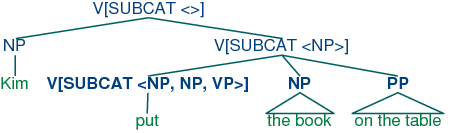 |
10.4.2 Heads Revisited
We noted in the previous section that by factoring subcategorization information out of the main category label, we could express more generalizations about properties of verbs. Another property of this kind is the following: expressions of category v are heads of phrases of category vp. Similarly (and more informally) ns are heads of nps, as (i.e., adjectives) are heads of aps, and ps (i.e., adjectives) are heads of pps. Not all phrases have heads — for example, it is standard to say that coordinate phrases (e.g., the book and the bell) lack heads — nevertheless, we would like our grammar formalism to express the mother / head-daughter relation where it holds. Now, although it looks as though there is something in common between, say, v and vp, this is more of a handy convention than a real claim, since v and vp formally have no more in common than v and Det.
X-bar syntax (cf. [Jacobs & Rosenbaum, 1970], [Jackendoff, 1977]) addresses this issue by abstracting out the notion of phrasal level. It is usual to recognize three such levels. If n represents the lexical level, then n' represents the next level up, corresponding to the more traditional category Nom, while n'' represents the phrasal level, corresponding to the category np. (The primes here replace the typographically more demanding horizontal bars of [Jacobs & Rosenbaum, 1970]). (126) illustrates a representative structure.
| (126) | 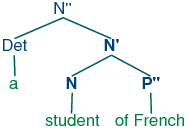 |
The head of the structure (126) is n while n' and n'' are called (phrasal) projections of n. n'' is the maximal projection, and n is sometimes called the zero projection. One of the central claims of X-bar syntax is that all constituents share a structural similarity. Using x as a variable over n, v, a and p, we say that directly subcategorized complements of the head are always placed as sisters of the lexical head, whereas adjuncts are placed as sisters of the intermediate category, x'. Thus, the configuration of the p'' adjunct in (127) contrasts with that of the complement p'' in (126).
| (127) | 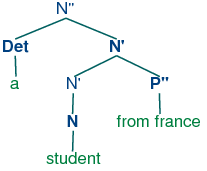 |
The productions in (128) illustrate how bar levels can be encoded using feature structures.
| (128) | s → n[bar=2] v[bar=2] n[bar=2] → Det n[bar=1] n[bar=1] → n[bar=1] p[bar=2] n[bar=1] → n[bar=0] p[bar=2] |
10.4.3 Auxiliary Verbs and Inversion
Inverted clauses — where the order of subject and verb is switched — occur in English interrogatives and also after 'negative' adverbs:
| (129) |
|
| (130) |
|
However, we cannot place just any verb in pre-subject position:
| (131) |
|
| (132) |
|
Verbs that can be positioned initially in inverted clauses belong to the class known as auxiliaries, and as well as do, can and have include be, will and shall. One way of capturing such structures is with the following production:
| (133) | S[+inv] -> V[+AUX] NP VP |
That is, a clause marked as [+inv] consists of an auxiliary verb followed by a vp. (In a more detailed grammar, we would need to place some constraints on the form of the vp, depending on the choice of auxiliary.) (134) illustrates the structure of an inverted clause.
| (134) | 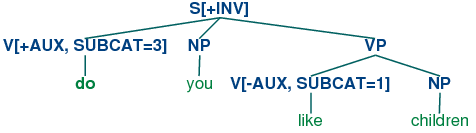 |
10.4.4 Unbounded Dependency Constructions
Consider the following contrasts:
| (135) |
|
| (136) |
|
The verb like requires an np complement, while put requires both a following np and pp. Examples (135) and (136) show that these complements are obligatory: omitting them leads to ungrammaticality. Yet there are contexts in which obligatory complements can be omitted, as (137) and (138) illustrate.
| (137) |
|
| (138) |
|
That is, an obligatory complement can be omitted if there is an appropriate filler in the sentence, such as the question word who in (137a), the preposed topic this music in (137b), or the wh phrases which card/slot in (138). It is common to say that sentences like (137) – (138) contain gaps where the obligatory complements have been omitted, and these gaps are sometimes made explicit using an underscore:
| (139) |
|
So, a gap can occur if it is licensed by a filler. Conversely, fillers can only occur if there is an appropriate gap elsewhere in the sentence, as shown by the following examples.
| (140) |
|
| (141) |
|
The mutual co-occurence between filler and gap leads to (137) – (138) is sometimes termed a "dependency". One issue of considerable importance in theoretical linguistics has been the nature of the material that can intervene between a filler and the gap that it licenses; in particular, can we simply list a finite set of strings that separate the two? The answer is No: there is no upper bound on the distance between filler and gap. This fact can be easily illustrated with constructions involving sentential complements, as shown in (142).
| (142) |
|
Since we can have indefinitely deep recursion of sentential complements, the gap can be embedded indefinitely far inside the whole sentence. This constellation of properties leads to the notion of an unbounded dependency construction; that is, a filler-gap dependency where there is no upper bound on the distance between filler and gap.
A variety of mechanisms have been suggested for handling unbounded dependencies in formal grammars; we shall adopt an approach due to Generalized Phrase Structure Grammar that involves something called slash categories. A slash category is something of the form y/xp; we interpret this as a phrase of category y that is missing a sub-constituent of category xp. For example, s/np is an s that is missing an np. The use of slash categories is illustrated in (143).
| (143) | 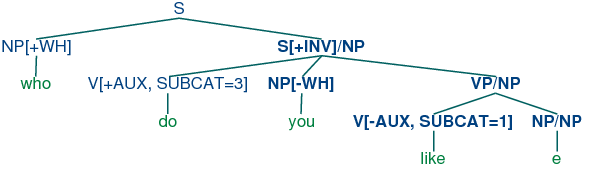 |
The top part of the tree introduces the filler who (treated as an expression of category np[+wh]) together with a corresponding gap-containing constituent s/np. The gap information is then "percolated" down the tree via the vp/np category, until it reaches the category np/np. At this point, the dependency is discharged by realizing the gap information as the empty string e immediately dominated by np/np.
Do we need to think of slash categories as a completely new kind of object in our grammars? Fortunately, no, we don't — in fact, we can accommodate them within our existing feature-based framework. We do this by treating slash as a feature, and the category to its right as a value. In other words, our "official" notation for s/np will be s[slash=NP]. Once we have taken this step, it is straightforward to write a small grammar for analyzing unbounded dependency constructions. 10.4 illustrates the main principles of slash categories, and also includes productions for inverted clauses. To simplify presentation, we have omitted any specification of tense on the verbs.
| ||
Listing 10.4 (slashcfg.py): Grammar for Simple Long-distance Dependencies |
The grammar in Listing 10.4 contains one gap-introduction production, namely
| (144) | s[-inv] → np s/np |
In order to percolate the slash feature correctly, we need to add slashes with variable values to both sides of the arrow in productions that expand s, vp and np. For example,
| (145) | vp/?x → v s-bar/?x |
says that a slash value can be specified on the vp mother of a constituent if the same value is also specified on the s-bar daughter. Finally, (146) allows the slash information on np to be discharged as the empty string.
| (146) |
np/np →
|
Using 10.4, we can parse the string who do you claim that you like into the tree shown in (147).
| (147) | 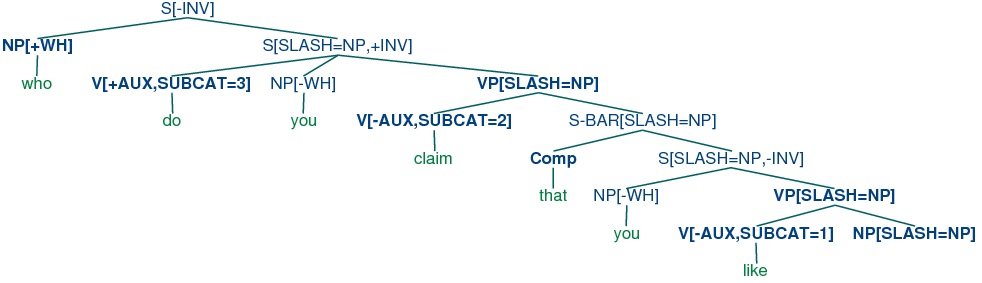 |
10.4.5 Case and Gender in German
Compared with English, German has a relatively rich morphology for agreement. For example, the definite article in German varies with case, gender and number, as shown in Table 10.2.
| Case | Masc | Fem | Neut | Plural |
| Nom | der | die | das | die |
| Gen | des | der | des | der |
| Dat | dem | der | dem | den |
| Acc | den | die | das | die |
Subjects in German take the nominative case, and most verbs govern their objects in the accusative case. However, there are exceptions like helfen that govern the dative case:
| (148) |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The grammar 10.5 illustrates the interaction of agreement (comprising person, number and gender) with case.
| ||
Listing 10.5 (germancfg.py): Example Feature-Based Grammar |
- As you will see, the feature objcase is used to
- specify the case that the verb governs on its object.
10.4.6 Exercises
☼ Modify the grammar illustrated in (120) to incorporate a bar feature for dealing with phrasal projections.
☼ Modify the German grammar in 10.5 to incorporate the treatment of subcategorization presented in 10.4.1.
◑ Extend the German grammar in 10.5 so that it can handle so-called verb-second structures like the following:
(149) Heute sieht der hund die katze.
★ Morphological paradigms are rarely completely regular, in the sense of every cell in the matrix having a different realization. For example, the present tense conjugation of the lexeme walk only has two distinct forms: walks for the 3rd person singular, and walk for all other combinations of person and number. A successful analysis should not require redundantly specifying that 5 out of the 6 possible morphological combinations have the same realization. Propose and implement a method for dealing with this.
★ So-called head features are shared between the mother and head daughter. For example, tense is a head feature that is shared between a vp and its head v daughter. See [Gazdar et al, 1985] for more details. Most of the features we have looked at are head features — exceptions are subcat and slash. Since the sharing of head features is predictable, it should not need to be stated explicitly in the grammar productions. Develop an approach that automatically accounts for this regular behavior of head features.
10.5 Summary
- The traditional categories of context-free grammar are atomic symbols. An important motivation feature structures is to capture fine-grained distinctions that would otherwise require a massive multiplication of atomic categories.
- By using variables over feature values, we can express constraints in grammar productions that allow the realization of different feature specifications to be inter-dependent.
- Typically we specify fixed values of features at the lexical level and constrain the values of features in phrases to unify with the corresponding values in their daughters.
- Feature values are either atomic or complex. A particular sub-case of atomic value is the Boolean value, represented by convention as [+/- f].
- Two features can share a value (either atomic or complex). Structures with shared values are said to be re-entrant. Shared values are represented by numerical indices (or tags) in AVMs.
- A path in a feature structure is a tuple of features corresponding to the labels on a sequence of arcs from the root of the graph representation.
- Two paths are equivalent if they share a value.
- Feature structures are partially ordered by subsumption. FS0 subsumes FS1 when FS0 is more general (less informative) than FS1.
- The unification of two structures FS0 and FS1, if successful, is the feature structure FS2 that contains the combined information of both FS0 and FS1.
- If unification specializes a path π in FS, then it also specializes every path π' equivalent to π.
- We can use feature structures to build succinct analyses of a wide variety of linguistic phenomena, including verb subcategorization, inversion constructions, unbounded dependency constructions and case government.
10.6 Further Reading
For more examples of feature-based parsing with NLTK, please see the guides at http://nltk.org/doc/guides/featgram.html, http://nltk.org/doc/guides/featstruct.html, and http://nltk.org/doc/guides/grammartestsuites.html.
For an excellent introduction to the phenomenon of agreement, see [Corbett, 2006].
The earliest use of features in theoretical linguistics was designed to capture phonological properties of phonemes. For example, a sound like /b/ might be decomposed into the structure [+labial, +voice]. An important motivation was to capture generalizations across classes of segments; for example, that /n/ gets realized as /m/ preceding any +labial consonant. Within Chomskyan grammar, it was standard to use atomic features for phenomena like agreement, and also to capture generalizations across syntactic categories, by analogy with phonology. A radical expansion of the use of features in theoretical syntax was advocated by Generalized Phrase Structure Grammar (GPSG; [Gazdar et al, 1985]), particularly in the use of features with complex values.
Coming more from the perspective of computational linguistics, [Dahl & Saint-Dizier, 1985] proposed that functional aspects of language could be captured by unification of attribute-value structures, and a similar approach was elaborated by [Grosz & Stickel, 1983] within the PATR-II formalism. Early work in Lexical-Functional grammar (LFG; [Bresnan, 1982]) introduced the notion of an f-structure that was primarily intended to represent the grammatical relations and predicate-argument structure associated with a constituent structure parse. [Shieber, 1986] provides an excellent introduction to this phase of research into feature-based grammars.
One conceptual difficulty with algebraic approaches to feature structures arose when researchers attempted to model negation. An alternative perspective, pioneered by [Kasper & Rounds, 1986] and [Johnson, 1988], argues that grammars involve descriptions of feature structures rather than the structures themselves. These descriptions are combined using logical operations such as conjunction, and negation is just the usual logical operation over feature descriptions. This description-oriented perspective was integral to LFG from the outset (cf. [Huang & Chen, 1989], and was also adopted by later versions of Head-Driven Phrase Structure Grammar (HPSG; [Sag & Wasow, 1999]). A comprehensive bibliography of HPSG literature can be found at http://www.cl.uni-bremen.de/HPSG-Bib/.
Feature structures, as presented in this chapter, are unable to capture important constraints on linguistic information. For example, there is no way of saying that the only permissible values for num are sg and pl, while a specification such as [num=masc] is anomalous. Similarly, we cannot say that the complex value of agr must contain specifications for the features per, num and gnd, but cannot contain a specification such as [subcat=3]. Typed feature structures were developed to remedy this deficiency. To begin with, we stipulate that feature values are always typed. In the case of atomic values, the values just are types. For example, we would say that the value of num is the type num. Moreover, num is the most general type of value for num. Since types are organized hierarchically, we can be more informative by specifying the value of num is a subtype of num, namely either sg or pl.
In the case of complex values, we say that feature structures are themselves typed. So for example the value of agr will be a feature structure of type agr. We also stipulate that all and only per, num and gnd are appropriate features for a structure of type agr. A good early review of work on typed feature structures is [Emele & Zajac, 1990]. A more comprehensive examination of the formal foundations can be found in [Carpenter, 1992], while [Copestake, 2002] focuses on implementing an HPSG-oriented approach to typed feature structures.
There is a copious literature on the analysis of German within feature-based grammar frameworks. [Nerbonne, Netter, & Pollard, 1994] is a good starting point for the HPSG literature on this topic, while [M{\"u}ller, 2002] gives a very extensive and detailed analysis of German syntax in HPSG.
Chapter 15 of [Jurafsky & Martin, 2008] discusses feature structures, the unification algorithm, and the integration of unification into parsing algorithms.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
11 Logical Semantics
11.1 Introduction
There are many NLP applications where it would be useful to have some representation of the meaning of a natural language sentence. For instance, current search engine technology can only take us so far in giving concise and correct answers to many questions that we might be interested in. Admittedly, Google does a good job in answering (150a), since its first hit is (150b).
| (150) |
|
By contrast, the result of sending (151) to Google is less helpful:
| (151) | Which countries border the Mediterranean? |
This time, the topmost hit (and the only relevant one in the top ten) presents the relevant information as a map of the Mediterranean basin. Since the map is an image file, it is not easy to extract the required list of countries from the returned page.
Even if Google succeeds in finding documents which contain information relevant to our question, there is no guarantee that it will be in a form which can be easily converted into an appropriate answer. One reason for this is that the information may have to be inferred from more than one source. This is likely to be the case when we seek an answer to more complex questions like (152):
| (152) | Which Asian countries border the Mediterranean? |
Here, we would probably need to combine the results of two subqueries, namely (151) and Which countries are in Asia?.
The example queries we have just given are based on a paper dating back to 1982 [Warren & Pereira, 1982]; this describes a system, Chat-80, which converts natural language questions into a semantic representation, and uses the latter to retrieve answers from a knowledge base. A knowledge base is usually taken to be a set of sentences in some formal language; in the case of Chat-80, it is a set of Prolog clauses. However, we can encode knowledge in a variety of formats, including relational databases, various kinds of graph, and first-order models. In NLTK, we have used the third of these options to re-implement a limited version of Chat-80:
Sentence: which Asian countries border the_Mediterranean ------------------------------ \x.((contain(asia, x) & country (x)) & border (x, mediterranean) set(['turkey', 'syria', 'israel', 'lebanon'])
As we will explain later in this chapter, a semantic representation of the form \x.P(x) denotes a set of entities u that meet some condition P(x). We then ask our knowledge base to enumerate all the entities in this set.
Let's assume more generally that knowledge is available in some structured fashion, and that it can be interrogated by a suitable query language. Then the challenge for NLP is to find a method for converting natural language questions into the target query language. An alternative paradigm for question answering is to take something like the pages returned by a Google query as our 'knowledge base' and then to carry out further analysis and processing of the textual information contained in the returned pages to see whether it does in fact provide an answer to the question. In either case, it is very useful to be able to build a semantic representation of questions. This NLP challenge intersects in interesting ways with one of the key goals of linguistic theory, namely to provide a systematic correspondence between form and meaning.
A widely adopted approach to representing meaning — or at least, some aspects of meaning — involves translating expressions of natural language into first-order logic (FOL). From a computational point of view, a strong argument in favor of FOL is that it strikes a reasonable balance between expressiveness and logical tractability. On the one hand, it is flexible enough to represent many aspects of the logical structure of natural language. On the other hand, automated theorem proving for FOL has been well studied, and although inference in FOL is not decidable, in practice many reasoning problems are efficiently solvable using modern theorem provers (cf. [Blackburn & Bos, 2005] for discussion).
While there are numerous subtle and difficult issues about how to translate natural language constructions into FOL, we will largely ignore these. The main focus of our discussion will be on a different issue, namely building semantic representations which conform to some version of the Principle of Compositionality. (See [Gleitman & Liberman, 1995] for this formulation.)
- Principle of Compositionality:
- The meaning of a whole is a function of the meanings of the parts and of the way they are syntactically combined.
There is an assumption here that the semantically relevant parts of a complex expression will be determined by a theory of syntax. Within this chapter, we will take it for granted that expressions are parsed against a context-free grammar. However, this is not entailed by the Principle of Compositionality. To summarize, we will be concerned with the task of systematically constructing a semantic representation in a manner that can be smoothly integrated with the process of parsing.
The overall framework we are assuming is illustrated in Figure (153). Given a syntactic analysis of a sentence, we can build one or more semantic representations for the sentence. Once we have a semantic representation, we can also check whether it is true in a model.
| (153) | 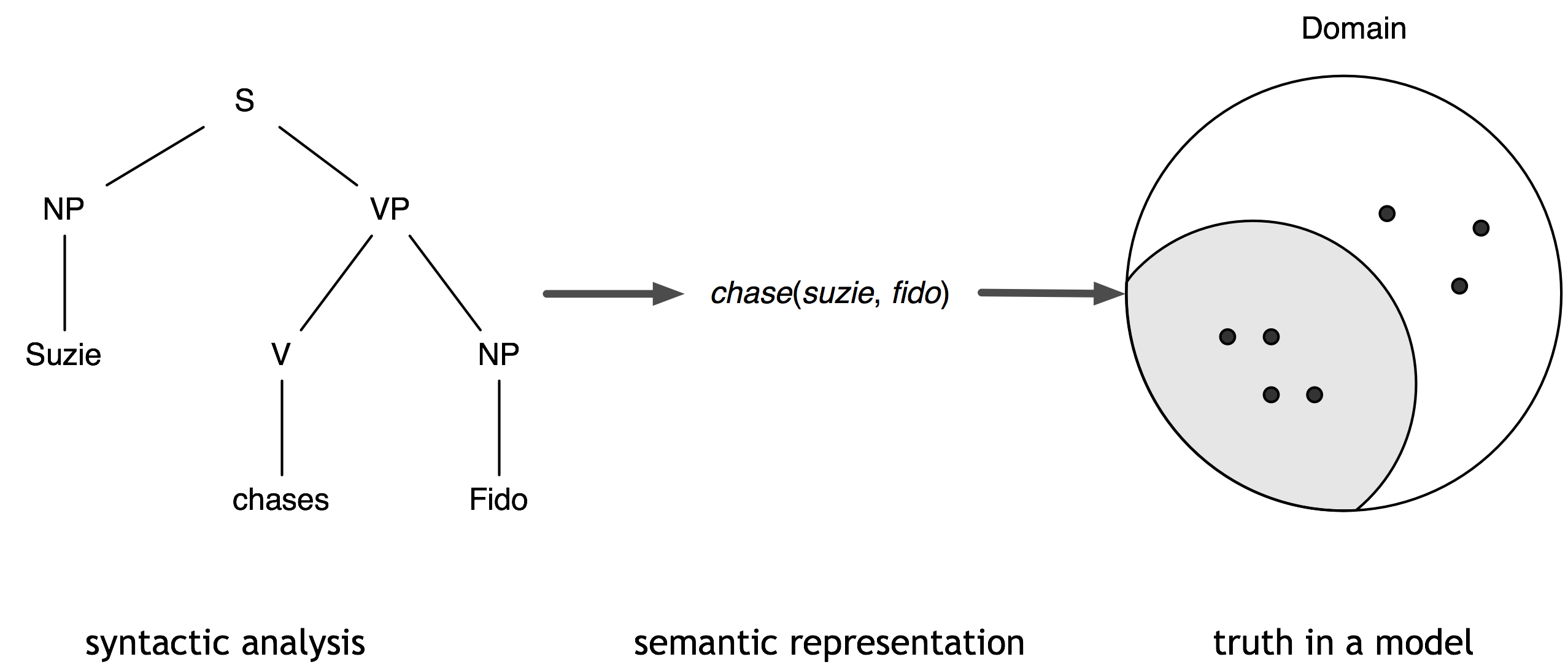 |
A model for a logical language is a set-theoretic construction which provides a very simplified picture of how the world is. For example, in this case, the model should contain individuals (indicated in the diagram by small dots) corresponding to Suzie and Fido, and it should also specify that these individuals belong to the chase relation.
The order of sections in this chapter is not what you might expect from looking at the diagram. We will start off in the middle of (153) by presenting a logical language that will provide us with semantic representations in NLTK. Next, we will show how formulas in the language can be systematically evaluated in a model. At the end, we will bring everything together and describe a simple method for constructing semantic representations as part of the parse process in NLTK.
11.2 Propositional Logic
The language of propositional logic represents certain aspects of natural language, but at a high level of abstraction. The only structure that is made explicit involves logical connectives; these correspond to 'logically interesting' expressions such as and and not. The basic expressions of the language are propositional variables, usually written p, q, r, etc. Let A be a finite set of such variables. There is a disjoint set of logical connectives which contains the unary operator ¬ (not), and binary operators ∧ (and), ∨ (or), → (implies) and ≡ (iff).
The set of formulas of Lprop is described inductively:
- Every element of A is a formula of Lprop.
- If φ is a formula of Lprop , then so is ¬ φ.
- If φ and ψ are formulas, then so are (φ ∧ ψ), (φ ∨ ψ), (φ → ψ) and (φ ≡ ψ).
- Nothing else is a formula of Lprop.
Within Lprop, we can construct formulas such as
| (154) | p → q ∨ r |
There are many sentences of English which could be taken to have the logical structure shown in (154). Here's an example:
| (155) | If it is raining, then Kim will take an umbrella or Lee will get wet. |
In order to explain the relation between (154) and (155), we need to give a key which maps between propositional variables and English sentences:
| (156) | p stands for it is raining, q for Kim will take an umbrella and q for Lee will get wet. |
The Boolean connectives of propositional logic are supported by the sem package, and are parsed into various kinds of Expression. We use -, &, |, ->, <-> to stand, respectively, for not, and, or, implies and iff. In the following example, we start off by creating a new instance lp of the NLTK LogicParser().
|
As the name suggests, propositional logic only studies the logical structure of formulas made up of atomic propositions. We saw, for example, that propositional variables stood for whole clauses in English. In order to look at how predicates combine with arguments, we need to look at a more complex language for semantic representation, namely first-order logic. In order to show how this new language interacts with the λ-calculus, it will be useful to introduce the notion of types into our syntactic definition, in departure from the rather simple approach to defining the clauses of Lprop.
In the general case, we interpret sentences of a logical language relative to a model, which is a very simplified version of the world. A model for propositional logic needs to assign the values True or False to every possible formula. We do this inductively: first, every propositional variable is assigned a value, and then we compute the value of complex formulas by consulting the meanings of the Boolean connectives and applying them to the values of the formula's components. Let's create a valuation:
|
We initialize a Valuation with a list of pairs, each of which consists of a semantic symbol and a semantic value. The resulting object is essentially just a dictionary that maps logical expressions (treated as strings) to appropriate values.
|
The keys of the dictionary (sorted alphabetically) can also be accessed via the property symbols:
|
As we will see later, our models need to be somewhat more complicated in order to handle the more complicated expressions discussed in the next section, so for the time being, just ignore the dom1 and g1 variables in the following declarations.
|
Now, let's create a model m that uses ``val1:
|
The prop=True is just a flag to say that our models are intended for propositional logic.
Every instance of Model defines appropriate truth functions for the Boolean connectives (and in fact they are implemented as functions named AND(), IMPLIES() and so on).
|
We can use these functions to create truth tables:
|
11.3 First-Order Logic
11.3.1 Predication
In first-order logic (FOL), propositions are analyzed into predicates and arguments, which takes us a step closer to the structure of natural languages. The standard construction rules for FOL recognize terms such as individual variables and individual constants, and predicates which take differing numbers of arguments. For example, Adam walks might be formalized as walk(adam) and Adam sees Betty as see(adam, betty). We will call walk a unary predicate, and see a binary predicate. Semantically, see is usually modeled as a relation, i.e., a set of pairs, and the proposition is true in a situation just in case the ordered pair pair 〈a, b〉 belongs to this set.
There is an alternative approach in which predication is treated as function application. In this functional style of representation, Adam sees Betty can be formalized as see(j)(m). That is, rather than being modeled as a relation, see denotes a function which applies to one argument to yield a new function that is then applied to the second argument. In NLTK, we will in fact treat predications syntactically as function applications, but we use a concrete syntax that allows them to represented as n-ary relations.
|
Relations are represented semantically in NLTK in the standard set-theoretic way: as sets of tuples. For example, let's suppose we have a domain of discourse consisting of the individuals Adam, Betty and Fido, where Adam is a boy, Betty is a girl and Fido is a dog. For mnemonic reasons, we use b1, g1 and d1 as the corresponding labels in the model. We can declare the domain as follows:
|
As before, we are going to initialize a valuation with a list of (symbol, value) pairs:
|
So according to this valuation, the value of see is a set of tuples such that Adam sees Betty, Fido sees Adam, and Betty sees Fido.
You may have noticed that our unary predicates (i.e, boy, girl, dog) also come out represented as sets of singleton tuples, rather than just sets of individuals. This is a convenience which allows us to have a uniform treatment of relations of any arity. In order to combine a unary relation with an argument, we use the function app(). If the input relation is unary, then app() returns a Boolean value; if the input is n-ary, for n > 1, then app() returns an n-1-ary relation.
|
11.3.2 Individual Variables and Assignments
In FOL, arguments of predicates can also be individual variables such as x, y and z. These can be thought of as similar to personal pronouns like he, she and it, in that we need to know about the context of use in order to figure out their denotation. In our models, the counterpart of a context of use is a variable Assignment. This is a mapping from individual variables to entities in the domain. Assignments are created using the Assignment constructor, which also takes the model's domain of discourse as a parameter. We are not required to actually enter any bindings, but if we do, they are in a (variable, value) format similar to what we say earlier for valuations.
|
In addition, there is a print() format for assignments which uses a notation closer to that in logic textbooks:
|
Let's now look at how we can evaluate an atomic formula of FOL. First, we create a model, then we use the evaluate() method to compute the truth value.
|
What's happening here? Essentially, we are making a call to app(app(see, 'g1'), 'd1') just as in our earlier example. However, when the interpretation function encounters the variable 'y', rather than checking for a value in val2, it asks the variable assignment g to come up with a value:
|
Since we already know that 'b1' and 'g1' stand in the see relation, the value True is what we expected. In this case, we can say that assignment g satisfies the formula 'see(adam, y)'. By contrast, the following formula evaluates to False relative to g — check that you see why this is.
|
In our approach (though not in standard first-order logic), variable assignments are partial. For example, g says nothing about any variables apart from 'x' and 'y'''. The method ``purge() clears all bindings from an assignment.
|
If we now try to evaluate a formula such as 'see(adam, y)' relative to g, it is like trying to interpret a sentence containing a she when we don't know what she refers to. In this case, the evaluation function fails to deliver a truth value.
|
11.3.3 Quantification and Scope
First-order logic standardly offers us two quantifiers, all (or every) and some. These are formally written as ∀ and ∃, respectively. At the syntactic level, quantifiers are used to bind individual variables like 'x' and 'y'. The following two sets of examples show a simple English example, a logical representation, and the encoding which is accepted by the NLTK logic module.
| (157) |
|
| (158) |
|
In the (158c), the quantifier some binds both occurences of the variable 'x'. As a result, (158c) is said to be a closed formula. By contrast, if we look at the body of (158c), the variables are unbound:
| (159) | girl(x) & walk(x) |
(159) is said to be an open formula. As we saw earlier, the interpretation of open formulas depends on the particular variable assignment that we are using.
One of the crucial insights of modern logic is that the notion of variable satisfaction can be used to provide an interpretation to quantified formulas. Let's continue to use (158c) as an example. When is it true? Let's think about all the individuals in our domain, i.e., in dom2. We want to check whether any of these individuals have the property of being a girl and walking. In other words, we want to know if there is some u in dom2 such that g[u/x] satisfies the open formula (159). Consider the following:
|
evaluate() returns True here because there is some u in dom2 such that (159) is satisfied by an assigment which binds 'x' to u. In fact, g1 is such a u:
|
One useful tool offered by NLTK is the satisfiers() method. This lists all the individuals that satisfy an open formula. The method parameters are a parsed formula, a variable, and an assignment. Here are a few examples:
|
It's useful to think about why fmla2 and fmla3 receive the values they do. In particular, recall the truth conditions for -> (encoded via the function IMPLIES() in every model):
|
This means that fmla2 is equivalent to this:
| (160) | - girl(x) | walk(x) |
That is, (160) is satisfied by something which either isn't a girl or walks. Since neither b1 (Adam) nor d1 (Fido) are girls, according to model m2, they both satisfy the whole formula. And of course g1 satisfies the formula because g1 satisfies both disjuncts. Now, since every member of the domain of discourse satisfies fmla2, the corresponding universally quantified formula is also true.
|
In other words, a universally quantified formula ∀x.φ is true with respect to g just in case for every u, φ is true with respect to g[u/x].
11.3.4 Quantificatier Scope Ambiguity
What happens when we want to give a formal representation of a sentence with two quantifiers, such as the following?
| (161) | Every girl chases a dog. |
There are (at least) two ways of expressing (161) in FOL:
| (162) |
|
Can we use both of these? Then answer is Yes, but they have different meanings. (162b) is logically stronger than (162a): it claims that there is a unique dog, say Fido, which is chased by every girl. (162a), on the other hand, just requires that for every girl g, we can find some dog which d chases; but this could be a different dog in each case. We distinguish between (162a) and (162b) in terms of the scope of the quantifiers. In the first, ∀ has wider scope than ∃, while in (162b), the scope ordering is reversed. So now we have two ways of representing the meaning of (161), and they are both quite legitimate. In other words, we are claiming that (161) is ambiguous with respect to quantifier scope, and the formulas in (162) give us a formal means of making the two readings explicit. However, we are not just interested in associating two distinct representations with (161). We also want to show in detail how the two representations lead to different conditions for truth in a formal model.
In order to examine the ambiguity more closely, let's fix our valuation as follows:
|
We can use the graph in (163) to visualize the chase relation.
| (163) | 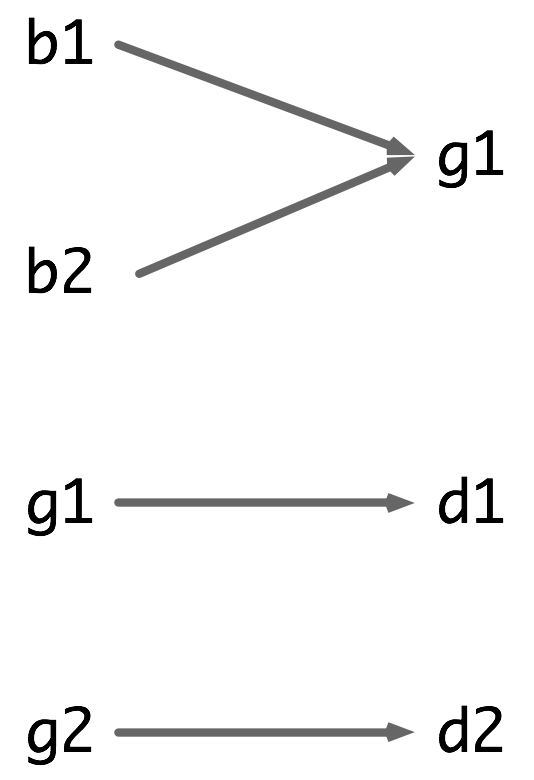 |
In (163), an arrow between two individuals x and y indicates that x chases y. So b1 and b2 both chase g1, while g1 chases d1 and g2 chases d2. In this model, formula scope2a_ above is true but scope2b_ is false. One way of exploring these results is by using the satisfiers() method of Model objects.
|
This gives us the set of individuals that can be assigned as the value of x in fmla1. In particular, every girl is included in this set. By contrast, consider the formula fmla2 below; this has no satisfiers for the variable y.
|
That is, there is no dog that is chased by both g1 and g2. Taking a slightly different open formula, fmla3, we can verify that there is a girl, namely g1, who is chased by every boy.
|
11.4 Evaluating English Sentences
11.4.1 Using the sem Feature
Until now, we have taken for granted that we have some appropriate logical formulas to interpret. However, ideally we would like to derive these formulas from natural language input. One relatively easy way of achieving this goal is to build on the grammar framework developed in Chapter 10. Our first step is to introduce a new feature, sem. Because values of sem generally need to be treated differently from other feature values, we use the convention of enclosing them in angle brackets. (164) illustrates a first approximation to the kind of analyses we would like to build.
| (164) |  |
Thus, the sem value at the root node shows a semantic representation for the whole sentence, while the sem values at lower nodes show semantic representations for constituents of the sentence. So far, so good, but how do we write grammar rules which will give us this kind of result? To be more specific, suppose we have a np and vp constituents with appropriate values for their sem nodes? If you reflect on the machinery that was introduced in discussing the λ calculus, you might guess that function application will be central to composing semantic values. You will also remember that our feature-based grammar framework gives us the means to refer to variable values. Putting this together, we can postulate a rule like (165) for building the sem value of an s. (Observe that in the case where the value of sem is a variable, we omit the angle brackets.)
| (165) | S[sem = <app(?vp,?subj)>] -> NP[sem=?subj] VP[sem=?vp] |
(165) tells us that given some sem value ?subj for the subject np and some sem value ?vp for the vp, the sem value of the s mother is constructed by applying ?vp as a functor to ?np. From this, we can conclude that ?vp has to denote a function which has the denotation of ?np in its domain; in fact, we are going to assume that ?vp denotes a curryed characteristic function on individuals. (165) is a nice example of building semantics using the principle of compositionality: that is, the principle that the semantics of a complex expression is a function of the semantics of its parts.
To complete the grammar is very straightforward; all we require are the rules shown in (166).
| (166) | VP[sem=?v] -> IV[sem=?v] NP[sem=<jane>] -> 'Jane' IV[sem=<walk>] -> 'walks' |
The vp rule says that the mother's semantics is the same as the head daughter's. The two lexical rules just introduce non-logical constants to serve as the semantic values of Jane and walks respectively. This grammar can be parsed using the chart parser in parse.featurechart, and the trace in (167) shows how semantic values are derived by feature unification in the process of building a parse tree.
| (167) | Predictor |> . .| S[sem='(?vp ?subj)'] -> * NP[sem=?subj] VP[sem=?vp] Scanner |[-] .| [0:1] 'Jane' Completer |[-> .| S[sem='(?vp john)'] -> NP[sem='john'] * VP[sem=?vp] Predictor |. > .| VP[sem=?v] -> * IV[sem=?v] Scanner |. [-]| [1:2] 'walks' Completer |. [-]| VP[sem='walk'] -> IV[sem='walk'] * Completer |[===]| S[sem='(walk john)'] -> NP[sem='john'] VP[sem='walk'] * Completer |[===]| [INIT] -> S * |
11.4.2 Quantified nps
You might be thinking this is all too easy — surely there is a bit more to building compositional semantics. What about quantifiers, for instance? Right, this is a crucial issue. For example, we want (168a) to be given a semantic representation like (168b). How can this be accomplished?
| (168) |
|
Let's make the assumption that our only operation for building complex semantic representations is function application. Then our problem is this: how do we give a semantic representation to quantified nps such as a dog so that they can be combined with something like 'walk' to give a result like (168b)? As a first step, let's make the subject's sem value act as the functor rather than the argument. Now we are looking for way of instantiating ?np so that (169a) is equivalent to (169b).
| (169) |
|
This is where λ abstraction comes to the rescue; doesn't (169) look a bit reminiscent of carrying out β-reduction in the λ-calculus? In other words, we want a λ term M to replace '?np' so that applying M to 'bark' yields (168b). To do this, we replace the occurence of 'bark' in (168b) by a variable 'P', and bind the variable with λ, as shown in (170).
| (170) | '\P.exists x.(dog(x) & P(x))' |
As a point of interest, we have used a different style of variable in (170), that is 'P' rather than 'x' or 'y'. This is to signal that we are abstracting over a different kind of thing — not an individual, but a function from Ind to Bool. So the type of (170) as a whole is ((Ind → Bool) → Bool). We will take this to be the type of nps in general. To illustrate further, a universally quantified np will look like (171).
| (171) | '\P.all x.(dog(x) -> P(x))' |
We are pretty much done now, except that we also want to carry out a further abstraction plus application for the process of combining the semantics of the determiner a with the semantics of dog. Applying (170) as a functor to 'bark' gives us '(\P.exists x.(dog (x) & P(x)) bark)', and carrying out β-reduction yields just what we wanted, namely (168b).
NLTK provides some utilities to make it easier to derive and inspect semantic interpretations. text_interpret() is intended for batch interpretation of a list of input sentences. It builds a dictionary d where for each sentence sent in the input, d[sent] is a list of paired trees and semantic representations for sent. The value is a list, since sent may be syntactically ambiguous; in the following example, we just look at the first member of the list.
|
By default, the semantic representation that is produced by text_interpret() has already undergone β-reduction, but in the above example, we have overridden this. Subsequent reduction is possible using the simplify() method, and Boolean connectives can be placed in infix position with the infixify() method.
|
11.4.3 Transitive Verbs
Our next challenge is to deal with sentences containing transitive verbs, such as (172).
| (172) | Suzie chases a dog. |
The output semantics that we want to build is shown in (173).
| (173) | 'exists x.(dog(x) & chase(suzie, x))' |
Let's look at how we can use λ-abstraction to get this result. A significant constraint on possible solutions is to require that the semantic representation of a dog be independent of whether the np acts as subject or object of the sentence. In other words, we want to get (173) as our output while sticking to (170) as the np semantics. A second constraint is that vps should have a uniform type of interpretation regardless of whether they consist of just an intransitive verb or a transitive verb plus object. More specifically, we stipulate that vps always denote characteristic functions on individuals. Given these constraints, here's a semantic representation for chases a dog which does the trick.
| (174) | '\y.exists x.(dog(x) & chase(y, x))' |
Think of (174) as the property of being a y such that for some dog x, y chases x; or more colloquially, being a y who chases a dog. Our task now resolves to designing a semantic representation for chases which can combine via app with (170) so as to allow (174) to be derived.
Let's carry out a kind of inverse β-reduction on (174), giving rise to (175).
Let Then we are part way to the solution if we can derive (175), where 'X' is applied to '\z.chase(y, z)'.
| (175) | '(\P.exists x.(dog(x) and P(x)) \z.chase(y, z))' |
(175) may be slightly hard to read at first; you need to see that it involves applying the quantified np representation from (170) to '\z.(chase z y))'. (175) is of course equivalent to (174).
Now let's replace the functor in (175) by a variable 'X' of the same type as an np; that is, of type ((Ind → Bool) → Bool).
| (176) | 'X(\z.chase(y, z))' |
The representation of a transitive verb will have to apply to an argument of the type of 'X' to yield a functor of the type of vps, that is, of type (Ind → Bool). We can ensure this by abstracting over both the 'X' variable in (176) and also the subject variable 'y'. So the full solution is reached by giving chases the semantic representation shown in (177).
| (177) | '\X y.X(\x.chase(y, x))' |
If (177) is applied to (170), the result after β-reduction is equivalent to (174), which is what we wanted all along:
| (178) | '(\X y.(X \x.(chase(y, x)) \P.exists x.(dog(x) & P(x))'
↝
'(\y.(\P.exists x.(dog(x) & P(x)) \x.chase(y, x))'
↝
'\y.(exists x.(dog(x) & chase(y, x)))'
|
In order to build a semantic representation for a sentence, we also need to combine in the semantics of the subject np. If the latter is a quantified expression like every girl, everything proceeds in the same way as we showed for a dog barks earlier on; the subject is translated as a functor which is applied to the semantic representation of the vp. However, we now seem to have created another problem for ourselves with proper names. So far, these have been treated semantically as individual constants, and these cannot be applied as functors to expressions like (174). Consequently, we need to come up with a different semantic representation for them. What we do in this case is re-interpret proper names so that they too are functors, like quantified nps. (179) shows the required λ expression for Suzie.
| (179) | '\P.P(suzie)' |
(179) denotes the characteristic function corresponding to the set of all properties which are true of Suzie. Converting from an individual constant to an expression like (177) is known as type raising, and allows us to flip functors with arguments. That is, type raising means that we can replace a Boolean-valued application such as (f a) with an equivalent application (λP.(P a) f).
One important limitation of the approach we have presented here is that it does not attempt to deal with scope ambiguity. Instead, quantifier scope ordering directly reflects scope in the parse tree. As a result, a sentence like (161), repeated here, will always be translated as (181a), not (181b).
| (180) | Every girl chases a dog. |
| (181) |
|
This limitation can be overcome, for example using the hole semantics described in [Blackburn & Bos, 2005], but discussing the details would take us outside the scope of the current chapter.
Now that we have looked at some slightly more complex constructions, we can evaluate them in a model. In the following example, we derive two parses for the sentence every boy chases a girl in Noosa, and evaluate each of the corresponding semantic representations in the model model0.py which we have imported.
|
11.5 Case Study: Extracting Valuations from Chat-80
Building Valuation objects by hand becomes rather tedious once we consider larger examples. This raises the question of whether the relation data in a Valuation could be extracted from some pre-existing source. The corpora.chat80 module provides an example of extracting data from the Chat-80 Prolog knowledge base (which included as part of the NLTK corpora distribution).
Chat-80 data is organized into collections of clauses, where each collection functions as a table in a relational database. The predicate of the clause provides the name of the table; the first element of the tuple acts as the 'key'; and subsequent elements are further columns in the table.
In general, the name of the table provides a label for a unary relation whose extension is all the keys. For example, the table in cities.pl contains triples such as (182).
| (182) | 'city(athens,greece,1368).' |
Here, 'athens' is the key, and will be mapped to a member of the unary relation city.
The other two columns in the table are mapped to binary relations, where the first argument of the relation is filled by the table key, and the second argument is filled by the data in the relevant column. Thus, in the city table illustrated by the tuple in (182), the data from the third column is extracted into a binary predicate population_of, whose extension is a set of pairs such as '(athens, 1368)'.
In order to encapsulate the results of the extraction, a class of Concepts is introduced. A Concept object has a number of attributes, in particular a prefLabel and extension, which make it easier to inspect the output of the extraction. The extension of a Concept object is incorporated into a Valuation object.
As well as deriving unary and binary relations from the Chat-80 data, we also create a set of individual constants, one for each entity in the domain. The individual constants are string-identical to the entities. For example, given a data item such as 'zloty', we add to the valuation a pair ('zloty', 'zloty'). In order to parse English sentences that refer to these entities, we also create a lexical item such as the following for each individual constant:
| (183) | PropN[num=sg, sem=<\P.P(zloty)>] -> 'Zloty' |
The chat80 module can be found in the corpora package. The attribute chat80.items gives us a list of Chat-80 relations:
|
The concepts() method shows the list of Concepts that can be extracted from a chat80 relation, and we can then inspect their extensions.
|
In order to convert such an extension into a valuation, we use the make_valuation() method; setting read=True creates and returns a new Valuation object which contains the results.
|
Note
Population figures are given in thousands. Bear in mind that the geographical data used in these examples dates back at least to the 1980s, and was already somewhat out of date at the point when [Warren & Pereira, 1982] was published.
11.6 Summary
- Semantic Representations (SRs) for English are constructed using a language based on the λ-calculus, together with Boolean connectives, equality, and first-order quantifiers.
- β-reduction in the λ-calculus corresponds semantically to application of a function to an argument. Syntactically, it involves replacing a variable bound by λ in the functor with the expression that provides the argument in the function application.
- If two λ-abstracts differ only in the label of the variable bound by λ, they are said to be α equivalents. Relabeling a variable bound by a λ is called α-conversion.
- Currying of a binary function turns it into a unary function whose value is again a unary function.
- FSRL has both a syntax and a semantics. The semantics is determined by recursively evaluating expressions in a model.
- A key part of constructing a model lies in building a valuation which assigns interpretations to non-logical constants. These are interpreted as either curried characteristic functions or as individual constants.
- The interpretation of Boolean connectives is handled by the model; these are interpreted as characteristic functions.
- An open expression is an expression containing one or more free variables. Open expressions only receive an interpretation when their free variables receive values from a variable assignment.
- Quantifiers are interpreted by constructing, for a formula φ[x] open in variable x, the set of individuals which make φ[x] true when an assignment g assigns them as the value of x. The quantifier then places constraints on that set.
- A closed expression is one that has no free variables; that is, the variables are all bound. A closed sentence is true or false with respect to all variable assignments.
- Given a formula with two nested quantifiers Q1 and Q2, the outermost quantifier Q1 is said to have wide scope (or scope over Q2). English sentences are frequently ambiguous with respect to the scope of the quantifiers they contain.
- English sentences can be associated with an SR by treating sem as a feature. The sem value of a complex expressions typically involves functional application of the sem values of the component expressions.
- Model valuations need not be built by hand, but can also be extracted from relational tables, as in the Chat-80 example.
11.7 Exercises
- ◑ Modify the sem.evaluate code so that it will give a helpful error message if an expression is not in the domain of a model's valuation function.
- ★ Specify and implement a typed functional language with quantifiers, Boolean connectives and equality. Modify sem.evaluate to interpret expressions of this language.
- ★ Extend the chat80 code so that it will extract data from a relational database using SQL queries.
- ★ Taking [WarrenPereira1982] as a starting point, develop a technique for converting a natural language query into a form that can be evaluated more efficiently in a model. For example, given a query of the form '(P(x) & Q(x)', convert it to '(Q(x) & P(x)' if the extension of 'Q' is smaller than the extension of 'P'.
11.8 Further Reading
For more examples of semantic analysis with NLTK, please see the guides at http://nltk.org/doc/guides/sem.html and http://nltk.org/doc/guides/logic.html.
The use of characteristic functions for interpreting expressions of natural language was primarily due to Richard Montague. [Dowty, Wall, & Peters, 1981] gives a comprehensive and reasonably approachable introduction to Montague's grammatical framework.
A more recent and wide-reaching study of the use of a λ based approach to natural language can be found in [Carpenter, 1997].
[Heim & Kratzer, 1998] is a thorough application of formal semantics to transformational grammars in the Government-Binding model.
[Blackburn & Bos, 2005] is the first textbook devoted to computational semantics, and provides an excellent introduction to the area.
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
12 Linguistic Data Management (DRAFT)
12.1 Introduction
Language resources of all kinds are proliferating on the Web. These include data such as lexicons and annotated text, and software tools for creating and manipulating the data. As we have seen in previous chapters, language resources are essential in most areas of NLP. This has been made possible by three significant technological developments over the past decade. First, inexpensive mass storage technology permits large resources to be stored in digital form, while the Extensible Markup Language (XML) and Unicode provide flexible ways to represent structured data and give it good prospects for long-term survival. Second, digital publication has been a practical and efficient means of sharing language resources. Finally, search engines, mailing lists, and online resource catalogs make it possible for people to discover the existence of the resources they may be seeking.
Together with these technological advances have been three other developments that have shifted the NLP community in the direction of data-intensive approaches. First, the "shared task method," an initiative of government sponsors, supports major sections within the community to identify a common goal for the coming year, and provides "gold standard" data on which competing systems can be evaluated. Second, data publishers such as the Linguistic Data Consortium have negotiated with hundreds of data providers (including newswire services in many countries), and created hundreds of annotated corpora stored in well-defined and consistent formats. Finally, organizations that purchase NLP systems, or that publish NLP papers, now expect the quality of the work to be demonstrated using standard datasets.
Although language resources are central to NLP, we still face many obstacles in using them. First, the resource we are looking for may not exist, and so we have to think about creating a new language resource, and doing a sufficiently careful job that it serves our future needs, thanks to its coverage, balance, and documentation of the sources. Second, a resource may exist but its creator didn't document its existence anywhere, leaving us to recreate the resource; however, to save further wasted effort we should learn about publishing metadata the documents the existence of a resource, and even how to publish the resource itself, in a form that is easy for others to re-use. Third, the resource may exist and may be obtained, but is in an incompatible format, and so we need to set about converting the data into a different format. Finally, the resource may be in the right format, but the available software is unable to perform the required analysis task, and so we need to develop our own program for analyzing the data. This chapter covers each of these issues — creating, publishing, converting, and analyzing — using many examples drawn from practical experience managing linguistic data. However, before embarking on this sequence of issues, we start by examining the organization of linguistic data.
12.2 Linguistic Databases
Linguistic databases span a multidimensional space of cases, which we can divide up in several ways: the scope and design of the data collection; the goals of the creators; the nature of the material included; the goals and methods of the users (which are often not anticipated by the creators). Three examples follow.
In one type of linguistic database, the design unfolds interactively in the course of the creator's explorations. This is the pattern typical of traditional "field linguistics," in which material from elicitation sessions is analyzed repeatedly as it is gathered, with tomorrow's elicitation often based on questions that arise in analyzing today's. The resulting field notes are then used during subsequent years of research, and may serve as an archival resource indefinitely — the field notes of linguists and anthropologists working in the early years of the 20th century remain an important source of information today. Computerization is an obvious boon to work of this type, as exemplified by the popular program Shoebox — now about two decades old and re-released as Toolbox — which replaces the field linguist's traditional shoebox full of file cards.
Another pattern is represented by experimental approaches in which a body of carefully-designed material is collected from a range of subjects, then analyzed to evaluate a hypothesis or develop a technology. Today, such databases are collected and analyzed in digital form. Among scientists (such as phoneticians or psychologists), they are rarely published and therefore rarely preserved. Among engineers, it has become common for such databases to be shared and re-used at least within a laboratory or company, and often to be published more widely. Linguistic databases of this type are the basis of the "common task" method of research management, which over the past 15 years has become the norm in government-funded research programs in speech- and language-related technology.
Finally, there are efforts to gather a "reference corpus" for a particular language. Large and well-documented examples include the American National Corpus (ANC) and the British National Corpus (BNC). The goal in such cases is to produce a set of linguistic materials that cover the many forms, styles and uses of a language as widely as possible. The core application is typically lexicographic, that is, the construction of dictionaries based on a careful study of patterns of use. These corpora were constructed by large consortia spanning government, industry, and academia. Their planning and execution took more than five years, and indirectly involved hundreds of person-years of effort. There is also a long and distinguished history of other humanistic reference corpora, such the Thesaurus Linguae Graecae.
There are no hard boundaries among these categories. Accumulations of smaller bodies of data may come in time to constitute a sort of reference corpus, while selections from large databases may form the basis for a particular experiment. Further instructive examples follow.
A linguist's field notes may include extensive examples of many genres (proverbs, conversations, narratives, rituals, and so forth), and may come to constitute a reference corpus of modest but useful size. There are many extinct languages for which such material is all the data we will ever have, and many more endangered languages for which such documentation is urgently needed. Sociolinguists typically base their work on analysis of a set of recorded interviews, which may over time grow to create another sort of reference corpus. In some labs, the residue of decades of work may comprise literally thousands of hours of recordings, many of which have been transcribed and annotated to one extent or another. The CHILDES corpus, comprising transcriptions of parent-child interactions in many languages, contributed by many individual researchers, has come to constitute a widely-used reference corpus for language acquisition research. Speech technologists aim to produce training and testing material of broad applicability, and wind up creating another sort of reference corpus. To date, linguistic technology R&D has been the primary source of published linguistic databases of all sorts (see e.g. http://www.ldc.upenn.edu/).
As large, varied linguistic databases are published, phoneticians or psychologists are increasingly likely to base experimental investigations on balanced, focused subsets extracted from databases produced for entirely different reasons. Their motivations include the desire to save time and effort, the desire to work on material available to others for replication, and sometimes a desire to study more naturalistic forms of linguistic behavior. The process of choosing a subset for such a study, and making the measurements involved, is usually in itself a non-trivial addition to the database. This recycling of linguistic databases for new purposes is a normal and expected consequence of publication. For instance, the Switchboard database, originally collected for speaker identification research, has since been used as the basis for published studies in speech recognition, word pronunciation, disfluency, syntax, intonation and discourse structure.
At present, only a tiny fraction of the linguistic databases that are collected are published in any meaningful sense. This is mostly because publication of such material was both time-consuming and expensive, and because use of such material by other researchers was also both expensive and technically difficult. However, general improvements in hardware, software and networking have changed this, and linguistic databases can now be created, published, stored and used without inordinate effort or large expense.
In practice, the implications of these cost-performance changes are only beginning to be felt. The main problem is that adequate tools for creation, publication and use of linguistic data are not widely available. In most cases, each project must create its own set of tools, which hinders publication by researchers who lack the expertise, time or resources to make their data accessible to others. Furthermore, we do not have adequate, generally accepted standards for expressing the structure and content of linguistic databases. Without such standards, general-purpose tools are impossible — though at the same time, without available tools, adequate standards are unlikely to be developed, used and accepted. Just as importantly, there must be a critical mass of users and published material to motivate maintenance of data and access tools over time.
Relative to these needs, the present chapter has modest goals, namely to equip readers to take linguistic databases into their own hands by writing programs to help create, publish, transform and analyze the data. In the rest of this section we take a close look at the fundamental data types, an exemplary speech corpus, and the lifecycle of linguistic data.
Figure 12.1: Basic Linguistic Datatypes: Lexicons and Texts
12.2.1 Fundamental Data Types
Linguistic data management deals with a variety of data types, the most important being lexicons and texts. A lexicon is a database of words, minimally containing part of speech information and glosses. For many lexical resources, it is sufficient to use a record structure, i.e. a key plus one or more fields, as shown in Figure 12.1. A lexical resource could be a conventional dictionary or comparative wordlist, as illustrated. Several related linguistic data types also fit this model. For example in a phrasal lexicon, the key field is a phrase rather than a single word. A thesaurus can be derived from a lexicon by adding topic fields to the entries and constructing an index over those fields. We can also construct special tabulations (known as paradigms) to illustrate contrasts and systematic variation, as shown in Figure 12.1 for three verbs.
At the most abstract level, a text is a representation of a real or fictional speech event, and the time-course of that event carries over into the text itself. A text could be a small unit, such as a word or sentence, or a complete narrative or dialogue. It may come with annotations such as part-of-speech tags, morphological analysis, discourse structure, and so forth. As we saw in the IOB tagging technique (Chapter 6), it is possible to represent higher-level constituents using tags on individual words. Thus the abstraction of text shown in Figure 12.1 is sufficient.
12.2.2 Corpus Structure: a Case Study of TIMIT
The TIMIT corpus of read speech was the first annotated speech database to be widely distributed, and it has an especially clear organization. TIMIT was developed by a consortium including Texas Instruments and MIT (hence the name), and was designed to provide data for the acquisition of acoustic-phonetic knowledge and to support the development and evaluation of automatic speech recognition systems.
Like the Brown Corpus, which displays a balanced selection of text genres and sources, TIMIT includes a balanced selection of dialects, speakers, and materials. For each of eight dialect regions, 50 male and female speakers having a range of ages and educational backgrounds each read ten carefully chosen sentences. Two sentences, read by all speakers, were designed to bring out dialect variation:
| (184) |
|
The remaining sentences were chosen to be phonetically rich, involving all phones (sounds) and a comprehensive range of diphones (phone bigrams). Additionally, the design strikes a balance between multiple speakers saying the same sentence in order to permit comparison across speakers, and having a large range of sentences covered by the corpus to get maximal coverage of diphones. Thus, five sentences read by each speaker, are also read by six other speakers (comparability). The remaining three sentences read by each speaker were unique to that speaker (coverage).
NLTK includes a sample from the TIMIT corpus. You can access its documentation in the usual way, using help(corpus.timit). Print corpus.timit.items to see a list of the 160 recorded utterances in the corpus sample. Each item name has complex internal structure, as shown in Figure 12.2.
Figure 12.2: Structure of a TIMIT Identifier in the NLTK Corpus Package
Each item has a phonetic transcription, which can be accessed using the phones() method. We can access the corresponding word tokens in the customary way. Both access methods permit an optional argument offset=True which includes the start and end offsets of the corresponding span in the audio file.
|
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint (Note that some of the examples in this chapter have not yet been updated to work with NLTK-Lite version 0.9).
In addition to this text data, TIMIT includes a lexicon that provides the canonical pronunciation of every word:
|
This gives us a sense of what a speech processing system would have to do in producing or recognizing speech in this particular dialect (New England). Finally, TIMIT includes demographic data about the speakers, permitting fine-grained study of vocal, social, and gender characteristics.
|
TIMIT illustrates several key features of corpus design. First, the corpus contains two layers of annotation, at the phonetic and orthographic levels. In general, a text or speech corpus may be annotated at many different linguistic levels, including morphological, syntactic, and discourse levels. Moreover, even at a given level there may be different labeling schemes or even disagreement amongst annotators, such that we want to represent multiple versions. A second property of TIMIT is its balance across multiple dimensions of variation, for coverage of dialect regions and diphones. The inclusion of speaker demographics brings in many more independent variables, that may help to account for variation in the data, and which facilitate later uses of the corpus for purposes that were not envisaged when the corpus was created, e.g. sociolinguistics. A third property is that there is a sharp division between the original linguistic event captured as an audio recording, and the annotations of that event. The same holds true of text corpora, in the sense that the original text usually has an external source, and is considered to be an immutable artifact. Any transformations of that artifact which involve human judgment — even something as simple as tokenization — are subject to later revision, thus it is important to retain the source material in a form that is as close to the original as possible.
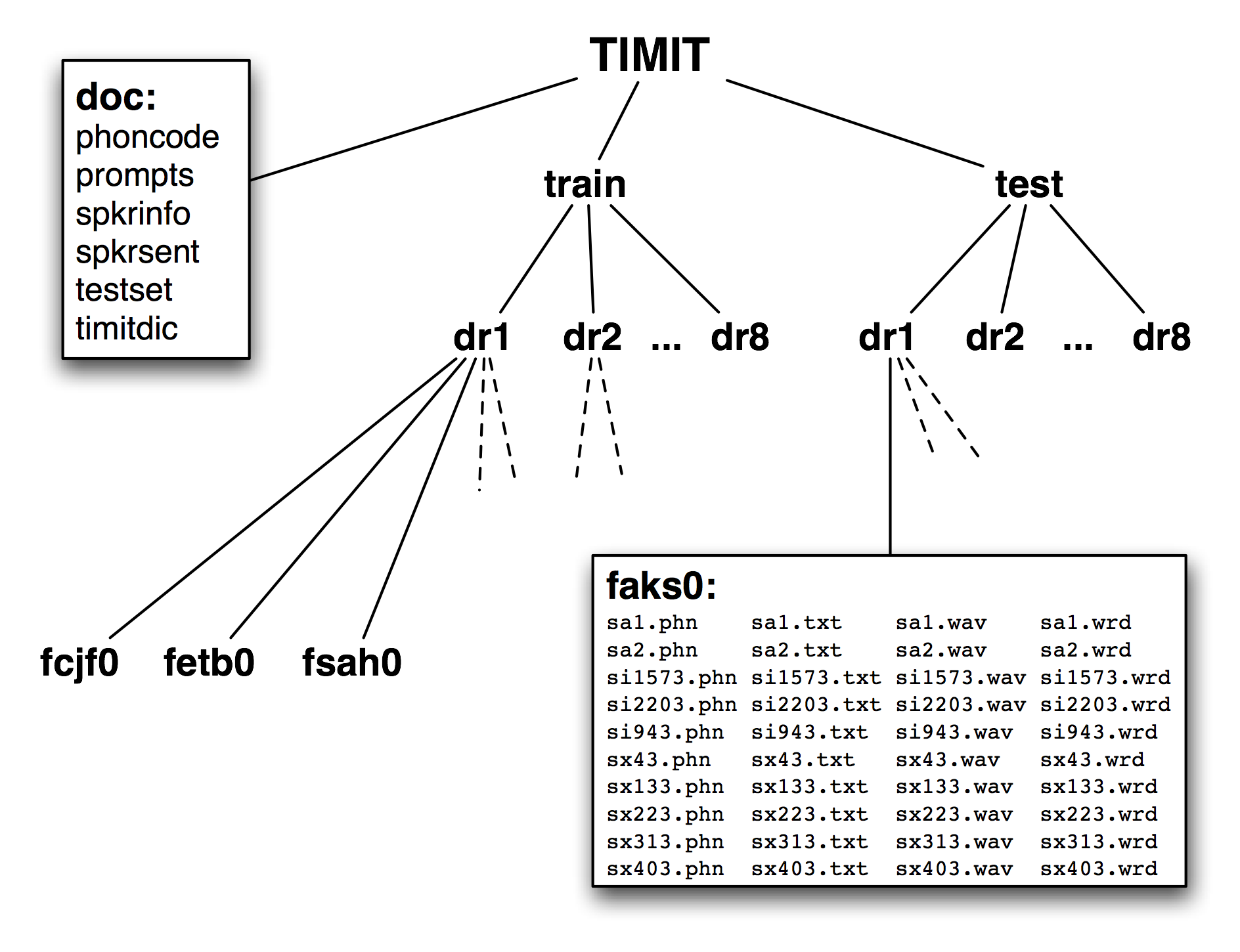
Figure 12.3: Structure of the Published TIMIT Corpus
A fourth feature of TIMIT is the hierarchical structure of the corpus. With 4 files per sentence, and 10 sentences for each of 500 speakers, there are 20,000 files. These are organized into a tree structure, shown schematically in Figure 12.3. At the top level there is a split between training and testing sets, which gives away its intended use for developing and evaluating statistical models.
Finally, notice that even though TIMIT is a speech corpus, its transcriptions and associated data are just text, and can be processed using programs just like any other text corpus. Therefore, many of the computational methods described in this book are applicable. Moreover, notice that all of the data types included in the TIMIT corpus fall into our two basic categories of lexicon and text (cf. section 12.2.1). Even the speaker demographics data is just another instance of the lexicon data type.
This last observation is less surprising when we consider that text and record structures are the primary domains for the two subfields of computer science that focus on data management, namely text retrieval and databases. A notable feature of linguistic data management is that usually brings both data types together, and that it can draw on results and techniques from both fields.
12.2.3 The Lifecycle of Linguistic Data: Evolution vs Curation
Once a corpus has been created and disseminated, it typically gains a life of its own, as others adapt it to their needs. This may involve reformatting a text file (e.g. converting to XML), renaming files, retokenizing the text, selecting a subset of the data to enrich, and so forth. Multiple research groups may do this work independently, as exemplified in Figure 12.4. At a later date, when someone wants to combine sources of information from different version, the task may be extremely onerous.
Figure 12.4: Evolution of a Corpus
The task of using derived corpora is made even more difficult by the lack of any record about how the derived version was created, and which version is the most up-to-date.
An alternative to this chaotic situation is for all corpora to be centrally curated, and for committees of experts to revise and extend a reference corpus at periodic intervals, considering proposals for new content from third-parties, much like a dictionary is edited. However, this is impractical.
A better solution is to have a canonical, immutable primary source, which supports incoming references to any sub-part, and then for all annotations (including segmentations) to reference this source. This way, two independent tokenizations of the same text can be represented without touch the source text, as can any further labeling and grouping of those annotations. This method is known as standoff annotation.
[More discussion and examples]
12.3 Creating Data
Scenarios: fieldwork, web, manual entry using local tool, machine learning with manual post-editing
Conventional office software is widely used in computer-based language documentation work, given its familiarity and ready availability. This includes word processors and spreadsheets.
12.3.1 Spiders
- what they do: basic idea is simple
- python code to find all the anchors, extract the href, and make an absolute URL for fetching
- many issues: starting points, staying within a single site, only getting HTML
- various stand-alone tools for spidering, and mirroring
12.3.2 Creating Language Resources Using Word Processors
Word processing software is often used in creating dictionaries and interlinear texts. As the data grows in size and complexity, a larger proportion of time is spent maintaining consistency. Consider a dictionary in which each entry has a part-of-speech field, drawn from a set of 20 possibilities, displayed after the pronunciation field, and rendered in 11-point bold. No conventional word processor has search or macro functions capable of verifying that all part-of-speech fields have been correctly entered and displayed. This task requires exhaustive manual checking. If the word processor permits the document to be saved in a non-proprietary format, such as text, HTML, or XML, we can sometimes write programs to do this checking automatically.
Consider the following fragment of a lexical entry: "sleep [sli:p] vi condition of body and mind...". We can enter this in MSWord, then "Save as Web Page", then inspect the resulting HTML file:
<p class=MsoNormal>sleep <span style='mso-spacerun:yes'> </span> [<span class=SpellE>sli:p</span>] <span style='mso-spacerun:yes'> </span> <b><span style='font-size:11.0pt'>vi</span></b> <span style='mso-spacerun:yes'> </span> <i>a condition of body and mind ...<o:p></o:p></i> </p>
Observe that the entry is represented as an HTML paragraph, using the <p> element, and that the part of speech appears inside a <span style='font-size:11.0pt'> element. The following program defines the set of legal parts-of-speech, legal_pos. Then it extracts all 11-point content from the dict.htm file and stores it in the set used_pos. Observe that the search pattern contains a parenthesized sub-expression; only the material that matches this sub-expression is returned by re.findall. Finally, the program constructs the set of illegal parts-of-speech as used_pos - legal_pos:
|
This simple program represents the tip of the iceberg. We can develop sophisticated tools to check the consistency of word processor files, and report errors so that the maintainer of the dictionary can correct the original file using the original word processor.
We can write other programs to convert the data into a different format. For example, Listing 12.1 strips out the HTML markup using ntlk.clean_html(), extracts the words and their pronunciations, and generates output in "comma-separated value" (CSV) format:
| ||
| ||
Listing 12.1 (html2csv.py): Converting HTML Created by Microsoft Word into Comma-Separated Values |
12.3.3 Creating Language Resources Using Spreadsheets and Databases
Spreadsheets. These are often used for wordlists or paradigms. A comparative wordlist may be stored in a spreadsheet, with a row for each cognate set, and a column for each language. Examples are available from www.rosettaproject.org. Programs such as Excel can export spreadsheets in the CSV format, and we can write programs to manipulate them, with the help of Python's csv module. For example, we may want to print out cognates having an edit-distance of at least three from each other (i.e. 3 insertions, deletions, or substitutions).
Databases. Sometimes lexicons are stored in a full-fledged relational database. When properly normalized, these databases can implement many well-formedness constraints. For example, we can require that all parts-of-speech come from a specified vocabulary by declaring that the part-of-speech field is an enumerated type. However, the relational model is often too restrictive for linguistic data, which typically has many optional and repeatable fields (e.g. dictionary sense definitions and example sentences). Query languages such as SQL cannot express many linguistically-motivated queries, e.g. find all words that appear in example sentences for which no dictionary entry is provided. Now supposing that the database supports exporting data to CSV format, and that we can save the data to a file dict.csv:
"sleep","sli:p","v.i","a condition of body and mind ..." "walk","wo:k","v.intr","progress by lifting and setting down each foot ..." "wake","weik","intrans","cease to sleep"
Now we can express this query as shown in Figure 12.2.
| ||
| ||
Listing 12.2 (undefined_words.py): Finding definition words not themselves defined |
12.3.4 Creating Language Resources Using Toolbox
Over the last two decades, several dozen tools have been developed that provide specialized support for linguistic data management. Perhaps the single most popular tool used by linguists for managing data is Toolbox, previously known as Shoebox (freely downloadable from http://www.sil.org/computing/toolbox/). In this section we discuss a variety of techniques for manipulating Toolbox data in ways that are not supported by the Toolbox software. (The methods we discuss could be applied to other record-structured data, regardless of the actual file format.)
A Toolbox file consists of a collection of entries (or records), where each record is made up of one or more fields. Here is an example of an entry taken from a Toolbox dictionary of Rotokas. (Rotokas is an East Papuan language spoken on the island of Bougainville; this data was provided by Stuart Robinson, and is a sample from a larger lexicon):
\lx kaa \ps N \pt MASC \cl isi \ge cooking banana \tkp banana bilong kukim \pt itoo \sf FLORA \dt 12/Aug/2005 \ex Taeavi iria kaa isi kovopaueva kaparapasia. \xp Taeavi i bin planim gaden banana bilong kukim tasol long paia. \xe Taeavi planted banana in order to cook it.
This lexical entry contains the following fields: lx lexeme; ps part-of-speech; pt part-of-speech; cl classifier; ge English gloss; tkp Tok Pisin gloss; sf Semantic field; dt Date last edited; ex Example sentence; xp Pidgin translation of example; xe English translation of example. These field names are preceded by a backslash, and must always appear at the start of a line. The characters of the field names must be alphabetic. The field name is separated from the field's contents by whitespace. The contents can be arbitrary text, and can continue over several lines (but cannot contain a line-initial backslash).
We can use the toolbox.xml() method to access a Toolbox file and load it into an elementtree object.
|
There are two ways to access the contents of the lexicon object, by indexes and by paths. Indexes use the familiar syntax, thus lexicon[3] returns entry number 3 (which is actually the fourth entry counting from zero). And lexicon[3][0] returns its first field:
|
The second way to access the contents of the lexicon object uses paths. The lexicon is a series of record objects, each containing a series of field objects, such as lx and ps. We can conveniently address all of the lexemes using the path record/lx. Here we use the findall() function to search for any matches to the path record/lx, and we access the text content of the element, normalizing it to lowercase.
|
It is often convenient to add new fields that are derived automatically from existing ones. Such fields often facilitate search and analysis. For example, in Listing 12.3 we define a function cv() which maps a string of consonants and vowels to the corresponding CV sequence, e.g. kakapua would map to CVCVCVV. This mapping has four steps. First, the string is converted to lowercase, then we replace any non-alphabetic characters [^a-z] with an underscore. Next, we replace all vowels with V. Finally, anything that is not a V or an underscore must be a consonant, so we replace it with a C. Now, we can scan the lexicon and add a new cv field after every lx field. Listing 12.3 shows what this does to a particular entry; note the last line of output, which shows the new CV field.
| ||
| ||
Listing 12.3 (add_cv_field.py): Adding a new cv field to a lexical entry |
Finally, we take a look at simple methods to generate summary reports, giving us an overall picture of the quality and organisation of the data.
First, suppose that we wanted to compute the average number of fields for each entry. This is just the total length of the entries (the number of fields they contain), divided by the number of entries in the lexicon:
|
| ||
| ||
Listing 12.4 (toolbox_validation.py): Validating Toolbox Entries Using a Context Free Grammar |
We could try to write down a grammar for lexical entries, and look for entries which do not conform to the grammar. In general, toolbox entries have nested structure. Thus they correspond to a tree over the fields. We can check for well-formedness by parsing the field names. In Listing 12.5 we set up a putative grammar for the entries, then parse each entry. Those that are accepted by the grammar prefixed with a '+', and those that are rejected are prefixed with a '-'.
| ||
| ||
Listing 12.5 (chunk_toolbox.py): Chunking a Toolbox Lexicon |
12.3.5 Interlinear Text
The NLTK corpus collection includes many interlinear text samples (though no suitable corpus reader as yet).
General Ontology for Linguistic Description (GOLD) http://www.linguistics-ontology.org/
12.3.6 Creating Metadata for Language Resources
OLAC metadata extends the Dublin Core metadata set with descriptors that are important for language resources.
The container for an OLAC metadata record is the element <olac>. Here is a valid OLAC metadata record from the Pacific And Regional Archive for Digital Sources in Endangered Cultures (PARADISEC):
<olac:olac xsi:schemaLocation="http://purl.org/dc/elements/1.1/ http://www.language-archives.org/OLAC/1.0/dc.xsd
http://purl.org/dc/terms/ http://www.language-archives.org/OLAC/1.0/dcterms.xsd
http://www.language-archives.org/OLAC/1.0/ http://www.language-archives.org/OLAC/1.0/olac.xsd">
<dc:title>Tiraq Field Tape 019</dc:title>
<dc:identifier>AB1-019</dc:identifier>
<dcterms:hasPart>AB1-019-A.mp3</dcterms:hasPart>
<dcterms:hasPart>AB1-019-A.wav</dcterms:hasPart>
<dcterms:hasPart>AB1-019-B.mp3</dcterms:hasPart>
<dcterms:hasPart>AB1-019-B.wav</dcterms:hasPart>
<dc:contributor xsi:type="olac:role" olac:code="recorder">Brotchie, Amanda</dc:contributor>
<dc:subject xsi:type="olac:language" olac:code="x-sil-MME"/>
<dc:language xsi:type="olac:language" olac:code="x-sil-BCY"/>
<dc:language xsi:type="olac:language" olac:code="x-sil-MME"/>
<dc:format>Digitised: yes;</dc:format>
<dc:type>primary_text</dc:type>
<dcterms:accessRights>standard, as per PDSC Access form</dcterms:accessRights>
<dc:description>SIDE A<p>1. Elicitation Session - Discussion and
translation of Lise's and Marie-Claire's Songs and Stories from
Tape 18 (Tamedal)<p><p>SIDE B<p>1. Elicitation Session: Discussion
of and translation of Lise's and Marie-Clare's songs and stories
from Tape 018 (Tamedal)<p>2. Kastom Story 1 - Bislama
(Alec). Language as given: Tiraq</dc:description>
</olac:olac>
NLTK Version 0.9 includes support for reading an OLAC record, for example:
|
12.3.7 Linguistic Annotation
Annotation graph model
multiple overlapping trees over shared data
Large annotation tasks require multiple annotators. How consistently can a group of annotators perform? It is insufficient to report that there is 80% agreement, as we have no way to tell if this is good or bad. I.e. for an easy task such as tagging, this would be a bad score, while for a difficult task such as semantic role labeling, this would be an exceptionally good score.
The Kappa coefficient K measures agreement between two people making category judgments, correcting for expected chance agreement. For example, suppose an item is to be annotated, and four coding options are equally likely. Then people coding randomly would be expected to agree 25% of the time. Thus, an agreement of 25% will be assigned K = 0, and better levels of agreement will be scaled accordingly. For an agreement of 50%, we would get K = 0.333, as 50 is a third of the way from 25 to 100.
12.3.8 Exercises
- ☼ Write a program to filter out just the date field (dt) without having to list the fields we wanted to retain.
- ☼ Print an index of a lexicon. For each lexical entry, construct a tuple of the form (gloss, lexeme), then sort and print them all.
- ☼ What is the frequency of each consonant and vowel contained in lexeme fields?
- ◑ In Listing 12.3 the new field appeared at the bottom of the entry. Modify this program so that it inserts the new subelement right after the lx field. (Hint: create the new cv field using Element('cv'), assign a text value to it, then use the insert() method of the parent element.)
- ◑ Write a function that deletes a specified field from a lexical entry. (We could use this to sanitize our lexical data before giving it to others, e.g. by removing fields containing irrelevant or uncertain content.)
- ◑ Write a program that scans an HTML dictionary file to find entries having an illegal part-of-speech field, and reports the headword for each entry.
- ◑ Write a program to find any parts of speech (ps field) that occurred less than ten times. Perhaps these are typing mistakes?
- ◑ We saw a method for discovering cases of whole-word reduplication. Write a function to find words that may contain partial reduplication. Use the re.search() method, and the following regular expression: (..+)\1
- ◑ We saw a method for adding a cv field. There is an interesting issue with keeping this up-to-date when someone modifies the content of the lx field on which it is based. Write a version of this program to add a cv field, replacing any existing cv field.
- ◑ Write a function to add a new field syl which gives a count of the number of syllables in the word.
- ◑ Write a function which displays the complete entry for a lexeme. When the lexeme is incorrectly spelled it should display the entry for the most similarly spelled lexeme.
- ◑ Write a function that takes a lexicon and finds which pairs of consecutive fields are most frequent (e.g. ps is often followed by pt). (This might help us to discover some of the structure of a lexical entry.)
- ★ Obtain a comparative wordlist in CSV format, and write a program that prints those cognates having an edit-distance of at least three from each other.
- ★ Build an index of those lexemes which appear in example sentences. Suppose the lexeme for a given entry is w. Then add a single cross-reference field xrf to this entry, referencing the headwords of other entries having example sentences containing w. Do this for all entries and save the result as a toolbox-format file.
12.4 Converting Data Formats
- write our own parser and formatted print
- use existing libraries, e.g. csv
12.4.1 Formatting Entries
We can also print a formatted version of a lexicon. It allows us to request specific fields without needing to be concerned with their relative ordering in the original file.
|
We can use the same idea to generate HTML tables instead of plain text. This would be useful for publishing a Toolbox lexicon on the web. It produces HTML elements <table>, <tr> (table row), and <td> (table data).
|
XML output
|
12.4.2 Exercises
- ◑ Create a spreadsheet using office software, containing one lexical entry per row, consisting of a headword, a part of speech, and a gloss. Save the spreadsheet in CSV format. Write Python code to read the CSV file and print it in Toolbox format, using lx for the headword, ps for the part of speech, and gl for the gloss.
12.5 Analyzing Language Data
I.e. linguistic exploration
Export to statistics package via CSV
In this section we consider a variety of analysis tasks.
Reduplication: First, we will develop a program to find reduplicated words. In order to do this we need to store all verbs, along with their English glosses. We need to keep the glosses so that they can be displayed alongside the wordforms. The following code defines a Python dictionary lexgloss which maps verbs to their English glosses:
|
Next, for each verb lex, we will check if the lexicon contains the reduplicated form lex+lex. If it does, we report both forms along with their glosses.
|
Complex Search Criteria: Phonological description typically identifies the segments, alternations, syllable canon and so forth. It is relatively straightforward to count up the occurrences of all the different types of CV syllables that occur in lexemes.
In the following example, we first import the regular expression and probability modules. Then we iterate over the lexemes to find all sequences of a non-vowel [^aeiou] followed by a vowel [aeiou].
|
Now, rather than just printing the syllables and their frequency counts, we can tabulate them to generate a useful display.
|
Consider the t and s columns, and observe that ti is not attested, while si is frequent. This suggests that a phonological process of palatalization is operating in the language. We would then want to consider the other syllables involving s (e.g. the single entry having su, namely kasuari 'cassowary' is a loanword).
Prosodically-motivated search: A phonological description may include an examination of the segmental and prosodic constraints on well-formed morphemes and lexemes. For example, we may want to find trisyllabic verbs ending in a long vowel. Our program can make use of the fact that syllable onsets are obligatory and simple (only consist of a single consonant). First, we will encapsulate the syllabic counting part in a separate function. It gets the CV template of the word cv(word) and counts the number of consonants it contains:
|
We also encapsulate the vowel test in a function, as this improves the readability of the final program. This function returns the value True just in case char is a vowel.
|
Over time we may create a useful collection of such functions. We can save them in a file utilities.py, and then at the start of each program we can simply import all the functions in one go using from utilities import *. We take the entry to be a verb if the first letter of its part of speech is a V. Here, then, is the program to display trisyllabic verbs ending in a long vowel:
|
Finding Minimal Sets: In order to establish a contrast segments (or lexical properties, for that matter), we would like to find pairs of words which are identical except for a single property. For example, the words pairs mace vs maze and face vs faze — and many others like them — demonstrate the existence of a phonemic distinction between s and z in English. NLTK provides flexible support for constructing minimal sets, using the MinimalSet() class. This class needs three pieces of information for each item to be added: context: the material that must be fixed across all members of a minimal set; target: the material that changes across members of a minimal set; display: the material that should be displayed for each item.
| Examples of Minimal Set Parameters | |||
|---|---|---|---|
| Minimal Set | Context | Target | Display |
| bib, bid, big | first two letters | third letter | word |
| deal (N), deal (V) | whole word | pos | word (pos) |
We begin by creating a list of parameter values, generated from the full lexical entries. In our first example, we will print minimal sets involving lexemes of length 4, with a target position of 1 (second segment). The context is taken to be the entire word, except for the target segment. Thus, if lex is kasi, then context is lex[:1]+'_'+lex[2:], or k_si. Note that no parameters are generated if the lexeme does not consist of exactly four segments.
|
Now we print the table of minimal sets. We specify that each context was seen at least 3 times.
|
Observe in the above example that the context, target, and displayed material were all based on the lexeme field. However, the idea of minimal sets is much more general. For instance, suppose we wanted to get a list of wordforms having more than one possible part-of-speech. Then the target will be part-of-speech field, and the context will be the lexeme field. We will also display the English gloss field.
|
The following program uses MinimalSet to find pairs of entries in the corpus which have different attachments based on the verb only.
|
Here is one of the pairs found by the program.
| (185) | received (NP offer) (PP from group) rejected (NP offer (PP from group)) |
This finding gives us clues to a structural difference: the verb receive usually comes with two following arguments; we receive something from someone. In contrast, the verb reject only needs a single following argument; we can reject something without needing to say where it originated from.
12.6 Summary
- diverse motivations for corpus collection
- corpus structure, balance, documentation
- OLAC
12.7 Further Reading
Shoebox/Toolbox and other tools for field linguistic data management: Full details of the Shoebox data format are provided with the distribution [Buseman, Buseman, & Early, 1996], and with the latest distribution, freely available from http://www.sil.org/computing/toolbox/. Many other software tools support the format. More examples of our efforts with the format are documented in [Tamanji, Hirotani, & Hall, 1999], [Robinson, Aumann, & Bird, 2007]. Dozens of other tools for linguistic data management are available, some surveyed by [Bird & Simons, 2003].
Some Major Corpora: The primary sources of linguistic corpora are the Linguistic Data Consortium and the European Language Resources Agency, both with extensive online catalogs. More details concerning the major corpora mentioned in the chapter are available: American National Corpus [Reppen, Ide, & Suderman, 2005], British National Corpus [{BNC}, 1999], Thesaurus Linguae Graecae [{TLG}, 1999], Child Language Data Exchange System (CHILDES) [MacWhinney, 1995], TIMIT [S., Lamel, & William, 1986]. The following papers give accounts of work on corpora that put them to entirely different uses than were envisaged at the time they were created [Graff & Bird, 2000], [Cieri & Strassel, 2002].
Annotation models and tools: An extensive set of models and tools are available, surveyed at http://www.exmaralda.org/annotation/. The initial proposal for standoff annotation was [Thompson & McKelvie, 1997]. The Annotation Graph model was proposed by [Bird & Liberman, 2001].
Scoring measures: Full details of the two scoring methods are available: Kappa: [Carletta, 1996], Windowdiff: [Pevzner & Hearst, 2002].
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
13 Conclusion
13.1 NLP and Intelligence
A long-standing challenge within computer science has been to build intelligent machines. The chief measure of machine intelligence has been a linguistic one, namely the Turing Test: can a dialogue system, responding to a user's typed input with its own textual output, perform so naturally that users cannot distinguish it from a human interlocutor using the same interface? Today, there is substantial ongoing research and development in such areas as machine translation and spoken dialogue, and significant commercial systems are in widespread use. The following dialogue illustrates a typical application:
Today's commercial dialogue systems are strictly limited to narrowly-defined domains. We could not ask the above system to provide driving instructions or details of nearby restaurants unless the requisite information had already been stored and suitable question and answer sentences had been incorporated into the language processing system. Observe that the above system appears to understand the user's goals: the user asks when a movie is showing and the system correctly determines from this that the user wants to see the movie. This inference seems so obvious to humans that we usually do not even notice it has been made, yet a natural language system needs to be endowed with this capability in order to interact naturally. Without it, when asked Do you know when Saving Private Ryan is playing, a system might simply — and unhelpfully — respond with a cold Yes. While it appears that this dialogue system can perform simple inferences, such sophistication is only found in cutting edge research prototypes. Instead, the developers of commercial dialogue systems use contextual assumptions and simple business logic to ensure that the different ways in which a user might express requests or provide information are handled in a way that makes sense for the particular application. Thus, whether the user says When is ..., or I want to know when ..., or Can you tell me when ..., simple rules will always yield screening times. This is sufficient for the system to provide a useful service.
As NLP technologies become more mature, and robust methods for analysing unrestricted text become more widespread, the prospect of natural language 'understanding' has re-emerged as a plausible goal. This has been brought into focus in recent years by a public 'shared task' called Recognizing Textual Entailment (RTE) [Quinonero-Candela et al, 2006]. The basic scenario is simple. Let's suppose we are interested in whether we can find evidence to support a hypothesis such as Sandra Goudie was defeated by Max Purnell. We are given another short text that appears to be relevant, for example, Sandra Goudie was first elected to Parliament in the 2002 elections, narrowly winning the seat of Coromandel by defeating Labour candidate Max Purnell and pushing incumbent Green MP Jeanette Fitzsimons into third place. The question now is whether the text provides sufficient evidence for us to accept the hypothesis as true. In this particular case, the answer is No. This is a conclusion that we can draw quite easily as humans, but it is very hard to come up with automated methods for making the right classification. The RTE Challenges provide data which allow competitors to develop their systems, but not enough data to allow statistical classifiers to be trained using standard machine learning techniques. Consequently, some linguistic analysis is crucial. In the above example, it is important for the system to note that Sandra Goudie names the person being defeated in the hypothesis, not the person doing the defeating in the text. As another illustration of the difficulty of the task, consider the following text/hypothesis pair:
- David Golinkin is the editor or author of eighteen books, and over 150 responsa, articles, sermons and books
- Golinkin has written eighteen books
In order to determine whether or not the hypothesis is supported by the text, the system needs at least the following background knowledge: (i) if someone is an author of a book, then he/she has written that book; (ii) if someone is an editor of a book, then he/she has not written that book; (iii) if someone is editor or author of eighteen books, then he/she is not author of eighteen books.
Despite the research-led advances in tasks like RTE, natural language systems that have been deployed for real-world applications still cannot perform common-sense reasoning or draw on world knowledge in a general and robust manner. We can wait for these difficult artificial intelligence problems to be solved, but in the meantime it is necessary to live with some severe limitations on the reasoning and knowledge capabilities of natural language systems. Accordingly, right from the beginning, an important goal of NLP research has been to make progress on the holy grail of natural linguistic interaction without recourse to this unrestricted knowledge and reasoning capability.
This has also been the goal of this book, and we hope that readers have been equipped with the knowledge and skills to build useful NLP systems, and to advance the field ever closer to its goal of providing intelligent NLP systems.
A Appendix: Regular Expressions
This section explores regular expressions in detail, with examples drawn from language processing. It builds on the brief overview given in the introductory programming chapter.
We have already noted that a text can be viewed as a string of characters. What kinds of processing are performed at the character level? Perhaps word games are the most familiar example of such processing. In completing a crossword we may want to know which 3-letter English words end with the letter c (e.g. arc). We might want to know how many words can be formed from the letters: a, c, e, o, and n (e.g. ocean). We may want to find out which unique English word contains the substring gnt (left as an exercise for the reader). In all these examples, we are considering which word - drawn from a large set of candidates - matches a given pattern. To put this in a more computational framework, we could imagine searching through a large digital corpus in order to find all words that match a particular pattern. There are many serious uses of this so-called pattern matching.
One instructive example is the task of finding all doubled words in a text; an example would be the string for for example. Notice that we would be particularly interested in finding cases where the words were split across a linebreak (in practice, most erroneously doubled words occur in this context). Consequently, even with such a relatively banal task, we need to be able to describe patterns which refer not just to "ordinary" characters, but also to formatting information.
There are conventions for indicating structure in strings, also known as formatting. For example, there are a number of alternative ways of formatting a "date string", such as 23/06/2002, 6/23/02, or 2002-06-23. Whole texts may be formatted, such as an email message which contains header fields followed by the message body. Another familiar form of formatting involves visual structure, such as tabular format and bulleted lists.
Finally, texts may contain explicit "markup", such as <abbrev>Phil</abbrev>, which provides information about the interpretation or presentation of some piece of text. To summarize, in language processing, strings are ubiquitous, and they often contain important structure.
So far we have seen elementary examples of pattern matching, the matching of individual characters. More often we are interested in matching sequences of characters. For example, part of the operation of a naive spell-checker could be to remove a word-final s from a suspect word token, in case the word is a plural, and see if the putative singular form exists in the dictionary. For this we must locate s and remove it, but only if it precedes a word boundary. This requires matching a pattern consisting of two characters.
Beyond this pattern matching on the content of a text, we often want to process the formatting and markup of a text. We may want to check the formatting of a document (e.g. to ensure that every sentence begins with a capital letter) or to reformat a document (e.g. replacing sequences of space characters with a single space). We may want to find all date strings and extract the year. We may want to extract all words contained inside the <abbrev> </abbrev> markup in order to construct a list of abbreviations.
Processing the content, format and markup of strings is a central task in most kinds of NLP. The most widespread method for string processing uses regular expressions.
A.1 Simple Regular Expressions
In this section we will see the building blocks for simple regular expressions, along with a selection of linguistic examples. We can think of a regular expression as a specialized notation for describing patterns that we want to match. In order to make explicit when we are talking about a pattern patt, we will use the notation «patt». The first thing to say about regular expressions is that most letters match themselves. For example, the pattern «sing» exactly matches the string sing. In addition, regular expressions provide us with a set of special characters [2] which give us a way to match sets of strings, and we will now look at these.
| [3] | These are often called meta-characters; that is, characters which express properties of (ordinary) characters. |
A.1.1 The Wildcard
The "." symbol is called a wildcard: it matches any single character. For example, the regular expression «s.ng» matches the following English words: sang, sing, song, and sung. Note that «.» will match not only alphabetic characters, but also numeric and whitespace characters. Consequently, «s.ng» will also match non-words such as s3ng.
We can also use the wildcard symbol for counting characters. For instance «....zy» matches six-letter strings that end in zy. The pattern «....berry» finds words like cranberry. In our text from Wall Street Journal below, the pattern «t...» will match the words that and term, and will also match the word sequence to a (since the third "." in the pattern can match the space character):
Paragraph 12 from wsj_0034: It's probably worth paying a premium for funds that invest in markets that are partially closed to foreign investors, such as South Korea, some specialists say. But some European funds recently have skyrocketed; Spain Fund has surged to a startling 120% premium. It has been targeted by Japanese investors as a good long-term play tied to 1992's European economic integration. And several new funds that aren't even fully invested yet have jumped to trade at big premiums. "I'm very alarmed to see these rich valuations," says Smith Barney's Mr. Porter.
Note
Note that the wildcard matches exactly one character, and must be repeated for as many characters as should be matched. To match a variable number of characters we must use notation for optionality.
We can see exactly where a regular expression matches against a string using NLTK's re_show function. Readers are encouraged to use re_show to explore the behavior of regular expressions.
|
A.1.2 Optionality and Repeatability
The "?" symbol indicates that the immediately preceding regular expression is optional. The regular expression «colou?r» matches both British and American spellings, colour and color. The expression that precedes the ? may be punctuation, such as an optional hyphen. For instance «e-?mail» matches both e-mail and email.
The "+" symbol indicates that the immediately preceding expression is repeatable, up to an arbitrary number of times. For example, the regular expression «coo+l» matches cool, coool, and so on. This symbol is particularly effective when combined with the . symbol. For example, «f.+f» matches all strings of length greater than two, that begin and end with the letter f (e.g. foolproof). The expression «.+ed» finds strings that potentially have the past-tense -ed suffix.
The "*" symbol indicates that the immediately preceding expression is both optional and repeatable. For example «.*gnt.*» matches all strings that contain gnt.
Occasionally we need to match material that spans a line-break. For example, we may want to strip out the HTML markup from a document. To do this we must delete material between angle brackets. The most obvious expression is: «<.*>». However, this has two problems: it will not match an HTML tag that contains a line-break, and the «.*» will consume as much material as possible (including the > character). To permit matching over a line-break we must use Python's DOTALL flag, and to ensure that the > matches against the first instance of the character we must do non-greedy matching using *?:
|
A.1.3 Choices
Patterns using the wildcard symbol are very effective, but there are many instances where we want to limit the set of characters that the wildcard can match. In such cases we can use the [] notation, which enumerates the set of characters to be matched - this is called a character class. For example, we can match any English vowel, but no consonant, using «[aeiou]». Note that this pattern can be interpreted as saying "match a or e or ... or u"; that is, the pattern resembles the wildcard in only matching a string of length one; unlike the wildcard, it restricts the characters matched to a specific class (in this case, the vowels). Note that the order of vowels in the regular expression is insignificant, and we would have had the same result with the expression «[uoiea]». As a second example, the expression «p[aeiou]t» matches the words: pat, pet, pit, pot, and put.
We can combine the [] notation with our notation for repeatability. For example, expression «p[aeiou]+t» matches the words listed above, along with: peat, poet, and pout.
Often the choices we want to describe cannot be expressed at the level of individual characters. As discussed in the tagging tutorial, different parts of speech are often tagged using labels from a tagset. In the Brown tagset, for example, singular nouns have the tag NN1, while plural nouns have the tag NN2, while nouns which are unspecified for number (e.g., aircraft) are tagged NN0. So we might use «NN.*» as a pattern which will match any nominal tag. Now, suppose we were processing the output of a tagger to extract string of tokens corresponding to noun phrases, we might want to find all nouns (NN.*), adjectives (JJ.*) and determiners (DT), while excluding all other word types (e.g. verbs VB.*). It is possible, using a single regular expression, to search for this set of candidates using the choice operator "|" as follows: «NN.*|JJ.*|DT». This says: match NN.* or JJ.* or DT.
As another example of multi-character choices, suppose that we wanted to create a program to simplify English prose, replacing rare words (like abode) with a more frequent, synonymous word (like home). In this situation, we need to map from a potentially large set of words to an individual word. We can match the set of words using the choice operator. In the case of the word home, we would want to match the regular expression «dwelling|domicile|abode».
Note
Note that the choice operator has wide scope, so that «123|456» is a choice between 123 and 456, and not between 12356 and 12456. The latter choice must be written using parentheses: «12(3|4)56».
A.2 More Complex Regular Expressions
In this section we will cover operators which can be used to construct more powerful and useful regular expressions.
A.2.1 Ranges
Earlier we saw how the [] notation could be used to express a set of choices between individual characters. Instead of listing each character, it is also possible to express a range of characters, using the - operator. For example, «[a-z]» matches any lowercase letter. This allows us to avoid the over-permissive matching we noted above with the pattern «t...». If we were to use the pattern «t[a-z][a-z][a-z]», then we would no longer match the two word sequence to a.
As expected, ranges can be combined with other operators. For example «[A-Z][a-z]*» matches words that have an initial capital letter followed by any number of lowercase letters. The pattern «20[0-4][0-9]» matches year expressions in the range 2000 to 2049.
Ranges can be combined, e.g. «[a-zA-Z]» which matches any lowercase or uppercase letter. The expression «[b-df-hj-np-tv-z]+» matches words consisting only of consonants (e.g. pygmy).
A.2.2 Complementation
We just saw that the character class «[b-df-hj-np-tv-z]+» allows us to match sequences of consonants. However, this expression is quite cumbersome. A better alternative is to say: let's match anything which isn't a vowel. To do this, we need a way of expressing complementation. We do this using the symbol "^" as the first character inside a class expression []. Let's look at an example. The regular expression « [^aeiou] » is just like our earlier character class «[aeiou]», except now the set of vowels is preceded by ^. The expression as a whole is interpreted as matching anything which fails to match «[aeiou]». In other words, it matches all lowercase consonants (plus all uppercase letters and non-alphabetic characters).
As another example, suppose we want to match any string which is enclosed by the HTML tags for boldface, namely <B> and </B>. We might try something like this: «<B>.*</B>». This would successfully match <B>important</B>, but would also match <B>important</B> and <B>urgent</B>, since the «.*» sub-pattern will happily match all the characters from the end of important to the end of urgent. One way of ensuring that we only look at matched pairs of tags would be to use the expression «<B>[^<]*</B>», where the character class matches anything other than a left angle bracket.
Finally, note that character class complementation also works with ranges. Thus «[^a-z]» matches anything other than the lower case alphabetic characters a through z.
A.2.3 Common Special Symbols
So far, we have only looked at patterns which match with the content of character strings. However, it is also useful to be able to refer to formatting properties of texts. Two important symbols in this regard are "^" and "$" which are used to anchor matches to the beginnings or ends of lines in a file.
Note
"^" has two quite distinct uses: it is interpreted as complementation when it occurs as the first symbol within a character class, and as matching the beginning of lines when it occurs elsewhere in a pattern.
For example, suppose we wanted to find all the words that occur at the beginning of lines in the WSJ text above. Our first attempt might look like «^[A-Za-z]+». This says: starting at the beginning of a line, look for one or more alphabetic characters (upper or lower case), followed by a space. This will match the words that, some, been, and even. However, it fails to match It's, since ' isn't an alphabetic character. A second attempt might be «^[^ ]+», which says to match any string starting at the beginning of a line, followed by one or more characters which are not the space character, followed by a space. This matches all the previous words, together with It's, skyrocketed, 1992s, I'm and "Mr.. As a second example, «[a-z]*s$» will match words ending in s that occur at the end of a line. Finally, consider the pattern «^$»; this matches strings where no character occurs between the beginning and the end of a line - in other words, empty lines!
As we have seen, special characters like ".", "*", "+" and "$" give us powerful means to generalize over character strings. But suppose we wanted to match against a string which itself contains one or more special characters? An example would be the arithmetic statement $5.00 * ($3.05 + $0.85). In this case, we need to resort to the so-called escape character "\" ("backslash"). For example, to match a dollar amount, we might use «\$[1-9][0-9]*\.[0-9][0-9]». The same goes for matching other special characters.
| Special Sequences | |
| \b | Word boundary (zero width) |
| \d | Any decimal digit (equivalent to [0-9]) |
| \D | Any non-digit character (equivalent to [^0-9]) |
| \s | Any whitespace character (equivalent to [ \t\n\r\f\v] |
| \S | Any non-whitespace character (equivalent to [^ \t\n\r\f\v]) |
| \w | Any alphanumeric character (equivalent to [a-zA-Z0-9_]) |
| \W | Any non-alphanumeric character (equivalent to [^a-zA-Z0-9_]) |
A.3 Python Interface
The Python re module provides a convenient interface to an underlying regular expression engine. The module allows a regular expression pattern to be compiled into a object whose methods can then be called. Let's begin by getting a list of English words:
|
Now we can compile a regular expression for words containing a sequence of two 'a's and find the matches:
|
Suppose now that we want to find all three-letter words ending in the letter "c". Our first attempt might be as follows:
|
The problem is that we have matched words containing three-letter sequences ending in "c" which occur anywhere within a word. For example, the pattern will match "c" in words like aback, Aerobacter and albacore. Instead, we must revise our pattern so that it is anchored to the beginning and ends of the word: «^...$»:
|
In the section on complementation, we briefly looked at the task of matching strings which were enclosed by HTML markup. Our first attempt is illustrated in the following code example, where we incorrectly match the whole string, rather than just the substring "<B>important</B>".
|
As we pointed out, one solution is to use a character class which matches with the complement of "<":
|
However, there is another way of approaching this problem. «<B>.*</B>» gets the wrong results because the «*» operator tries to consume as much input as possible. That is, the matching is said to be greedy. In the current case, «*» matches everything after the first <B>, including the following </B> and <B>. If we instead use the non-greedy star operator «*?», we get the desired match, since «*?» tries to consume as little input as possible.
A.3.1 Exercises
- Pig Latin is a simple transliteration of English: words starting with
a vowel have way appended (e.g. is becomes isway);
words beginning with a consonant have all consonants up to the first
vowel moved to the end of the word, and then ay is appended
(e.g. start becomes artstay).
- Write a program to convert English text to Pig Latin.
- Extend the program to convert text, instead of individual words.
- Extend it further to preserve capitalization, to keep qu together (i.e. so that quiet becomes ietquay), and to detect when y is used as a consonant (e.g. yellow) vs a vowel (e.g. style).
- An interesting challenge for tokenization is words that have been
split across a line-break. E.g. if long-term is split, then we
have the string long-\nterm.
- Write a regular expression that identifies words that are hyphenated at a line-break. The expression will need to include the \n character.
- Use re.sub() to remove the \n character from these words.
- Write a utility function that takes a URL as its argument, and returns the contents of the URL, with all HTML markup removed. Use urllib.urlopen to access the contents of the URL, e.g. raw_contents = urllib.urlopen('http://nltk.org/').read().
- Write a program to guess the number of syllables from the orthographic representation of words (e.g. English text).
- Download some text from a language that has vowel harmony (e.g. Hungarian), extract the vowel sequences of words, and create a vowel bigram table.
- Obtain a pronunciation lexicon, and try generating nonsense rhymes.
A.4 Further Reading
A.M. Kuchling. Regular Expression HOWTO, http://www.amk.ca/python/howto/regex/
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
B Appendix: Text Processing with Unicode
Our programs will often need to deal with different languages, and different character sets. The concept of "plain text" is a fiction. If you live in the English-speaking world you probably use ASCII, possibly without realizing it. If you live in Europe you might use one of the extended Latin character sets, containing such characters as "ø" for Danish and Norwegian, "ő" for Hungarian, "ñ" for Spanish and Breton, and "ň" for Czech and Slovak. In this section, we will give an overview of how to use Unicode for processing texts that use non-ASCII character sets.
B.1 What is Unicode?
Unicode supports over a million characters. Each of these characters is assigned a number, called a code point. In Python, code points are written in the form \uXXXX, where XXXX is the number in 4-digit hexadecimal form.
Within a program, Unicode code points can be manipulated directly, but when Unicode characters are stored in files or displayed on a terminal they must be encoded as one or more bytes. Some encodings (such as ASCII and Latin-2) use a single byte, so they can only support a small subset of Unicode, suited to a single language. Other encodings (such as UTF-8) use multiple bytes and can represent the full range of Unicode.
Text in files will be in a particular encoding, so we need some mechanism for translating it into Unicode — translation into Unicode is called decoding. Conversely, to write out Unicode to a file or a terminal, we first need to translate it into a suitable encoding — this translation out of Unicode is called encoding. The following diagram illustrates.
From a Unicode perspective, characters are abstract entities which can be realized as one or more glyphs. Only glyphs can appear on a screen or be printed on paper. A font is a mapping from characters to glyphs.
B.2 Extracting encoded text from files
Let's assume that we have a small text file, and that we know how it is encoded. For example, polish-lat2.txt, as the name suggests, is a snippet of Polish text (from the Polish Wikipedia; see http://pl.wikipedia.org/wiki/Biblioteka_Pruska), encoded as Latin-2, also known as ISO-8859-2. The function nltk.data.find() locates the file for us.
|
The Python codecs module provides functions to read encoded data into Unicode strings, and to write out Unicode strings in encoded form. The codecs.open() function takes an encoding parameter to specify the encoding of the file being read or written. So let's import the codecs module, and call it with the encoding 'latin2' to open our Polish file as Unicode.
|
For a list of encoding parameters allowed by codecs, see http://docs.python.org/lib/standard-encodings.html.
Text read from the file object f will be returned in Unicode. As we pointed out earlier, in order to view this text on a terminal, we need to encode it, using a suitable encoding. The Python-specific encoding unicode_escape is a dummy encoding that converts all non-ASCII characters into their \uXXXX representations. Code points above the ASCII 0-127 range but below 256 are represented in the two-digit form \xXX.
|
The first line above illustrates a Unicode escape string, namely preceded by the \u escape string, namely \u0144 . The relevant Unicode character will be dislayed on the screen as the glyph ń. In the third line of the preceding example, we see \xf3, which corresponds to the glyph ó, and is within the 128-255 range.
In Python, a Unicode string literal can be specified by preceding an ordinary string literal with a u, as in u'hello'. Arbitrary Unicode characters are defined using the \uXXXX escape sequence inside a Unicode string literal. We find the integer ordinal of a character using ord(). For example:
|
The hexadecimal 4 digit notation for 97 is 0061, so we can define a Unicode string literal with the appropriate escape sequence:
|
Notice that the Python print statement is assuming a default encoding of the Unicode character, namely ASCII. However, ń is outside the ASCII range, so cannot be printed unless we specify an encoding. In the following example, we have specified that print should use the repr() of the string, which outputs the UTF-8 escape sequences (of the form \xXX) rather than trying to render the glyphs.
|
If your operating system and locale are set up to render UTF-8 encoded characters, you ought to be able to give the Python command
print nacute_utf
and see ń on your screen.
Note
There are many factors determining what glyphs are rendered on your screen. If you are sure that you have the correct encoding, but your Python code is still failing to produce the glyphs you expected, you should also check that you have the necessary fonts installed on your system.
The module unicodedata lets us inspect the properties of Unicode characters. In the following example, we select all characters in the third line of our Polish text outside the ASCII range and print their UTF-8 escaped value, followed by their code point integer using the standard Unicode convention (i.e., prefixing the hex digits with U+), followed by their Unicode name.
|
If you replace the %r (which yields the repr() value) by %s in the format string of the code sample above, and if your system supports UTF-8, you should see an output like the following:
Alternatively, you may need to replace the encoding 'utf8' in the example by 'latin2', again depending on the details of your system.
The next examples illustrate how Python string methods and the re module accept Unicode strings.
|
The NLTK tokenizer module allows Unicode strings as input, and correspondingly yields Unicode strings as output.
|
B.3 Using your local encoding in Python
If you are used to working with characters in a particular local encoding, you probably want to be able to use your standard methods for inputting and editing strings in a Python file. In order to do this, you need to include the string '# -*- coding: <coding> -*-' as the first or second line of your file. Note that <coding> has to be a string like 'latin-1', 'big5' or 'utf-8'.
Note
If you are using Emacs as your editor, the coding specification will also be interpreted as a specification of the editor's coding for the file. Not all of the valid Python names for codings are accepted by Emacs.
The following screenshot illustrates the use of UTF-8 encoded string literals within the IDLE editor:

Note
The above example requires that an appropriate font is set in IDLE's preferences. In this case, we chose Courier CE.
The above example also illustrates how regular expressions can use encoded strings.
B.3.1 Further Reading
There are a number of online discussions of Unicode in general, and of Python facilities for handling Unicode. The following are worth consulting:
- Jason Orendorff, Unicode for Programmers, http://www.jorendorff.com/articles/unicode/.
- A. M. Kuchling, Unicode HOWTO, http://www.amk.ca/python/howto/unicode
- Frederik Lundh, Python Unicode Objects, http://effbot.org/zone/unicode-objects.htm
- Joel Spolsky, The Absolute Minimum Every Software Developer Absolutely, Positively Must Know About Unicode and Character Sets (No Excuses!), http://www.joelonsoftware.com/articles/Unicode.html
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
C Appendix: NLP in Python vs other Programming Languages
Many programming languages have been used for NLP. As explained in the Preface, we have chosen Python because we believe it is well-suited to the special requirements of NLP. Here we present a brief survey of several programming languages, for the simple task of reading a text and printing the words that end with ing. We begin with the Python version, which we believe is readily interpretable, even by non Python programmers:
import sys
for line in sys.stdin:
for word in line.split():
if word.endswith('ing'):
print word
Like Python, Perl is a scripting language. However, its syntax is obscure. For instance, it is difficult to guess what kind of entities are represented by: <>, $, my, and split, in the following program:
while (<>) {
foreach my $word (split) {
if ($word =~ /ing$/) {
print "$word\n";
}
}
}
We agree that "it is quite easy in Perl to write programs that simply look like raving gibberish, even to experienced Perl programmers" (Hammond 2003:47). Having used Perl ourselves in research and teaching since the 1980s, we have found that Perl programs of any size are inordinately difficult to maintain and re-use. Therefore we believe Perl is no longer a particularly suitable choice of programming language for linguists or for language processing.
Prolog is a logic programming language which has been popular for developing natural language parsers and feature-based grammars, given the inbuilt support for search and the unification operation which combines two feature structures into one. Unfortunately Prolog is not easy to use for string processing or input/output, as the following program code demonstrates for our linguistic example:
main :-
current_input(InputStream),
read_stream_to_codes(InputStream, Codes),
codesToWords(Codes, Words),
maplist(string_to_list, Words, Strings),
filter(endsWithIng, Strings, MatchingStrings),
writeMany(MatchingStrings),
halt.
codesToWords([], []).
codesToWords([Head | Tail], Words) :-
( char_type(Head, space) ->
codesToWords(Tail, Words)
;
getWord([Head | Tail], Word, Rest),
codesToWords(Rest, Words0),
Words = [Word | Words0]
).
getWord([], [], []).
getWord([Head | Tail], Word, Rest) :-
(
( char_type(Head, space) ; char_type(Head, punct) )
-> Word = [], Tail = Rest
; getWord(Tail, Word0, Rest), Word = [Head | Word0]
).
filter(Predicate, List0, List) :-
( List0 = [] -> List = []
; List0 = [Head | Tail],
( apply(Predicate, [Head]) ->
filter(Predicate, Tail, List1),
List = [Head | List1]
; filter(Predicate, Tail, List)
)
).
endsWithIng(String) :- sub_string(String, _Start, _Len, 0, 'ing').
writeMany([]).
writeMany([Head | Tail]) :- write(Head), nl, writeMany(Tail).
Java is an object-oriented language incorporating native support for the Internet, that was originally designed to permit the same executable program to be run on most computer platforms. Java has replaced COBOL as the standard language for business enterprise software:
import java.io.*;
public class IngWords {
public static void main(String[] args) throws Exception {
BufferedReader in = new BufferedReader(new
InputStreamReader(
System.in));
String line = in.readLine();
while (line != null) {
for (String word : line.split(" ")) {
if (word.endsWith("ing"))
System.out.println(word);
}
line = in.readLine();
}
}
}
The C programming language is a highly-efficient low-level language that is popular for operating system and networking software:
#include <stdio.h>
#include <string.h>
int main(int argc, char **argv) {
int i = 0;
int c = 1;
char buffer[1024];
while (c != EOF) {
c = fgetc(stdin);
if ( (c >= '0' && c <= '9') || (c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z') ) {
buffer[i++] = (char) c;
continue;
} else {
if (i > 2 && (strncmp(buffer+i-3, "ing", 3) == 0 || strncmp(buffer+i-3, "ING", 3) == 0 ) ) {
buffer[i] = 0;
puts(buffer);
}
i = 0;
}
}
return 0;
}
LISP is a so-called functional programming language, in which all objects are lists, and all operations are performed by (nested) functions of the form (function arg1 arg2 ...). Many of the earliest NLP systems were implemented in LISP:
(defpackage "REGEXP-TEST" (:use "LISP" "REGEXP"))
(in-package "REGEXP-TEST")
(defun has-suffix (string suffix)
"Open a file and look for words ending in _ing."
(with-open-file (f string)
(with-loop-split (s f " ")
(mapcar #'(lambda (x) (has_suffix suffix x)) s))))
(defun has_suffix (suffix string)
(let* ((suffix_len (length suffix))
(string_len (length string))
(base_len (- string_len suffix_len)))
(if (string-equal suffix string :start1 0 :end1 NIL :start2 base_len :end2 NIL)
(print string))))
(has-suffix "test.txt" "ing")
Ruby is a more recently developed scripting language than Python, best known for its convenient web application framework, Ruby on Rails. Here are two Ruby programs for finding words ending in ing
ARGF.each { |line|
line.split.find_all { |word|
word.match(/ing$/)
}.each { |word|
puts word
}
}
for line in ARGF
for word in line.split
if word.match(/ing$/) then
puts word
end
end
end
Haskell is another functional programming language which permits a much more compact (but incomprehensible) solution of our simple task:
import Data.List
main = putStr . unlines . filter ("ing" `isSuffixOf`) . words =<< getContent
The unix shell can also be used for simple linguistic processing. Here is a simple pipeline for finding the ing words. The first step transliterates any whitespace character to a newline, so that each word of the text occurs on its own line, and the second step finds all lines ending in ing
tr [:space:] '\n' | grep ing$
(We are grateful to the following people for furnishing us with these program samples: Tim Baldwin, Trevor Cohn, David Duke, Rod Farmer, Andrew Hardie, Aaron Harnly, Edward Ivanovic, and Lars Yencken.)
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
D Appendix: NLTK Modules and Corpora
NLTK Organization: NLTK is organized into a collection of task-specific packages. Each package is a combination of data structures for representing a particular kind of information such as trees, and implementations of standard algorithms involving those structures such as parsers. This approach is a standard feature of object-oriented design, in which components encapsulate both the resources and methods needed to accomplish a particular task.
The most fundamental NLTK components are for identifying and manipulating individual words of text. These include: tokenize, for breaking up strings of characters into word tokens; tag, for adding part-of-speech tags, including regular-expression taggers, n-gram taggers and Brill taggers; and the Porter stemmer.
The second kind of module is for creating and manipulating structured linguistic information. These components include: tree, for representing and processing parse trees; featurestructure, for building and unifying nested feature structures (or attribute-value matrices); cfg, for specifying context-free grammars; and parse, for creating parse trees over input text, including chart parsers, chunk parsers and probabilistic parsers.
Several utility components are provided to facilitate processing and visualization. These include: draw, to visualize NLP structures and processes; probability, to count and collate events, and perform statistical estimation; and corpora, to access tagged linguistic corpora.
A further group of components is not part of NLTK proper. These are a wide selection of third-party contributions, often developed as student projects at various institutions where NLTK is used, and distributed in a separate package called NLTK Contrib. Several of these student contributions, such as the Brill tagger and the HMM module, have now been incorporated into NLTK. Although these contributed components are not maintained, they may serve as a useful starting point for future student projects.
In addition to software and documentation, NLTK provides substantial corpus samples. Many of these can be accessed using the corpora module, avoiding the need to write specialized file parsing code before you can do NLP tasks. These corpora include: Brown Corpus — 1.15 million words of tagged text in 15 genres; a 10% sample of the Penn Treebank corpus, consisting of 40,000 words of syntactically parsed text; a selection of books from Project Gutenberg totally 1.7 million words; and other corpora for chunking, prepositional phrase attachment, word-sense disambiguation, text categorization, and information extraction.
| Corpora and Corpus Samples Distributed with NLTK | ||
|---|---|---|
| Corpus | Compiler | Contents |
| Alpino Dutch Treebank | van Noord | 140k words, tagged and parsed (Dutch) |
| Australian ABC News | Bird | 2 genres, 660k words, sentence-segmented |
| Brown Corpus | Francis, Kucera | 15 genres, 1.15M words, tagged, categorized |
| CESS-CAT Catalan Treebank | CLiC-UB et al | 500k words, tagged and parsed |
| CESS-ESP Spanish Treebank | CLiC-UB et al | 500k words, tagged and parsed |
| CMU Pronouncing Dictionary | CMU | 127k entries |
| CoNLL 2000 Chunking Data | Tjong Kim Sang | 270k words, tagged and chunked |
| CoNLL 2002 Named Entity | Tjong Kim Sang | 700k words, pos- and named-entity-tagged (Dutch, Spanish) |
| Floresta Treebank | Diana Santos et al | 9k sentences (Portuguese) |
| Genesis Corpus | Misc web sources | 6 texts, 200k words, 6 languages |
| Gutenberg (sel) | Hart, Newby, et al | 14 texts, 1.7M words |
| Indian POS-Tagged Corpus | Kumaran et al | 60k words, tagged (Bangla, Hindi, Marathi, Telugu) |
| MacMorpho Corpus | NILC, USP, Brazil | 1M words, tagged (Brazilian Portuguese) |
| Movie Reviews | Pang, Lee | Sentiment Polarity Dataset 2.0 |
| Names Corpus | Kantrowitz, Ross | 8k male and female names |
| NIST 1999 Info Extr (sel) | Garofolo | 63k words, newswire and named-entity SGML markup |
| NPS Chat Corpus | Forsyth, Martell | 10k IM chat posts, POS-tagged and dialogue-act tagged |
| PP Attachment Corpus | Ratnaparkhi | 28k prepositional phrases, tagged as noun or verb modifiers |
| Presidential Addresses | Ahrens | 485k words, formatted text |
| Proposition Bank | Palmer | 113k propositions, 3300 verb frames |
| Question Classification | Li, Roth | 6k questions, categorized |
| Reuters Corpus | Reuters | 1.3M words, 10k news documents, categorized |
| Roget's Thesaurus | Project Gutenberg | 200k words, formatted text |
| RTE Textual Entailment | Dagan et al | 8k sentence pairs, categorized |
| SEMCOR | Rus, Mihalcea | 880k words, part-of-speech and sense tagged |
| SENSEVAL 2 Corpus | Ted Pedersen | 600k words, part-of-speech and sense tagged |
| Shakespeare XML texts (sel) | Jon Bosak | 8 books |
| Stopwords Corpus | Porter et al | 2,400 stopwords for 11 languages |
| Switchboard Corpus (sel) | LDC | 36 phonecalls, transcribed, parsed |
| Univ Decl of Human Rights | 480k words, 300+ languages | |
| US Pres Addr Corpus | Ahrens | 480k words |
| Penn Treebank (sel) | LDC | 40k words, tagged and parsed |
| TIMIT Corpus (sel) | NIST/LDC | audio files and transcripts for 16 speakers |
| VerbNet 2.1 | Palmer et al | 5k verbs, hierarchically organized, linked to WordNet |
| Wordlist Corpus | OpenOffice.org et al | 960k words and 20k affixes for 8 languages |
| WordNet 3.0 (English) | Miller, Fellbaum | 145k synonym sets |
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
E Appendix: Python and NLTK Cheat Sheet (Draft)
E.1 Python
E.1.1 Strings
|
For more information, type help(str) at the Python prompt.
E.1.2 Lists
|
The following functions modify the list in-place:
|
For more information, type help(list) at the Python prompt.
E.1.3 Dictionaries
|
For more information, type help(dict) at the Python prompt.
E.1.4 Regular Expressions
Note
to be written
E.2 NLTK
Many more examples can be found in the NLTK Guides, available at http://nltk.org/doc/guides.
E.2.1 Corpora
|
E.2.2 Tokenization
|
E.2.3 Stemming
|
E.2.4 Tagging
Note
to be written
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is
Index
_
A
- A* Parser (8.4.2)
- A* parser (8.4.3)
- adjectives (3.5.1)
- adverbs (3.5.1)
- agreement (10.2.1)
- American National Corpus (12.2)
- appropriate (10.6)
- articles (3.5.1)
- artificial intelligence (1.1.2)
- assignment (1.3.2)
- Assignment (11.3.2)
- assigns (1.3.2)
- associative array (5.2.6)
- atomic (10.2.3)
- attribute value matrix (10.2.3)
- auxiliaries (10.4.3)
- auxiliary (10.2.3)
B
- backtracks (7.5.1)
- base (2.3.2)
- beam search (8.4.4)
- best-first search strategy (8.4.4)
- bigram (2.3.2)
- binary predicate (11.3.1)
- BIO Format (6.9)
- body (1.5.2)
- Boolean context (1.6.5)
- Boolean (1.6.2)
- boolean (10.2.3)
- bottom-up (5.5.3)
- Bottom-Up Initialization Rule (8.3.3)
- Bottom-Up Initialization Rule (8.3.3)
- bottom-up parsing (7.5.1)
- Bottom-Up Predict Rule (8.3.3)
- Bottom-Up Predict Rule (8.3.3)
- Bottom-Up Strategy (8.3.3)
- British National Corpus (12.2)
- business information analysis (1.1.2)
C
- call-by-value (5.4.2)
- call (1.4.1)
- call structure (5.5.3)
- cartesian product (5.2.5)
- Catalan numbers (8.1)
- characters (1.4)
- chart (8.2.2)
- chart parsing (8.2)
- chart parsing (8.2)
- child (7.3.3)
- CHILDES (12.2)
- chink (6.4.4)
- chink (6.9)
- chinking (6.4.4)
- chunker (6.3)
- chunking (6.1)
- chunks (6.1)
- closed class (3.5.2)
- closed formula (11.3.3)
- coindex (10.3.2)
- common nouns (3.2.2)
- complements (7.4.3)
- complete edge (8.3)
- complete (7.5.4)
- complete (8.4.4)
- complex (10.2.3)
- compound keys (5.2.6)
- computer science (1.1.2)
- concatenation (1.3.1)
- conditional expression (1.6.1)
- conditional frequency distribution (2.4.6)
- constituency (7.3.2)
- constituents (7.3.2)
- context-free grammar (7.4)
- control structure (1.5.2)
- control structure (1.6.1)
- conversion specifier (1.5.3)
- copy (5.2.1)
- corpus linguistics (1.1.2)
- Corpus Linguistics (2.4.2)
- count nouns (3.2.2)
- counters (1.7.2)
D
- data types (1.6.4)
- daughter (7.3.3)
- decorator (5.5.3)
- decrease-and-conquer (5.5)
- delimited (1.3.1)
- dependency grammar (7.4.4)
- derivation (7.4.5)
- determiners (3.5.1)
- diagnosis (6.8)
- dialogue (13.1)
- dictionary (1.7.1)
- direct recursion (7.4.2)
- directed acyclic graphs (10.3.2)
- divide-and-conquer (5.5)
- docstring (5.4)
- dot (8.3)
- dotted edges (8.3)
- Dublin Core (12.3.6)
- dynamic programming (8.2)
- dynamically typed (5.4.1)
E
F
- f-structure (10.6)
- feature (10.2.2)
- feature path (10.3.2)
- feature structure (10.2.3)
- fields (5.2.3)
- filler (10.4.4)
- first-in-first-out (5.2.4)
- format string (1.5.3)
- frequency distribution (2.4.1)
- function body (5.4)
- function (1.4.1)
- function (2.4.3)
- function (5.4)
- Fundamental Rule (8.3.2)
- Fundamental Rule (8.3.2)
G
H
I
- identifiers (1.3.3)
- immutable (1.5.1)
- immutable (5.2.3)
- immutable (5.2.6)
- import (1.5.4)
- incomplete edge (8.3)
- increment (1.5.2)
- index (1.4.1)
- indexing (1.4.1)
- indirect recursion (7.4.2)
- inference (13.1)
- inflected (2.3.2)
- Information Extraction (6.7)
- interpreter (1.2.1)
- intransitive (3.2.2)
- IOB tags (6.2.2)
- iteration (1.5.2)
K
L
- labeling (6.1)
- lambda expressions (5.4.5)
- Lancaster Stemmer (2.3.2)
- last-in-first-out (5.2.4)
- leaves (7.3.1)
- leaves (7.3.1)
- left-corner (7.5.3)
- left-corner parser (7.5.3)
- left recursive (7.4.2)
- lemma (2.3.2)
- lemma (2.3.2)
- Lemmatization (2.3.2)
- lexeme (2.3.2)
- lexical ambiguity (7.3.1)
- lexical categories (3.1)
- lexical productions (7.4.1)
- lexicon (12.2.1)
- licensed (10.4.4)
- licenses (7.4.1)
- linguistic category (10.2.3)
- List comprehensions (2.3.3)
- list (1.5.1)
- logical connectives (11.2)
- long-distance dependency (10.1)
- loop variable (1.5.2)
- lowest-cost-first search strategy (8.4.4)
M
- machine intelligence (13.1)
- majority class classifier (3.2.4)
- map (1.7)
- mass nouns (3.2.2)
- matches (1.8)
- maximal projection (10.4.2)
- memoization (5.5.3)
- method (I.5)
- methods (1.5.1)
- modals (3.5.1)
- model (11.1)
- module (1.5.4)
- morpho-syntactic (3.3.1)
- morphological (3.5.2)
- most likely constituents table (8.4.2)
- mutable (1.5.1)
- mutable (5.2.3)
- mutual information (2.4.7)
N
O
P
- parent (7.3.3)
- parse edge (8.3)
- parser (7.5)
- part-of-speech tagging (3.1)
- part-of-speech tags (3.1)
- partial information (10.3.3)
- partial parsing (6.2.1)
- parts of speech (3.1)
- past participle (3.3.1)
- personal pronouns (3.5.1)
- phrasal level (10.4.2)
- phrase structure (7.2)
- polysemous (2.5.1)
- Porter Stemmer (2.3.2)
- POS-tagging (3.1)
- POS tags (3.1)
- pre-sort (5.5)
- pre-terminals (7.4.1)
- precision/recall trade-off (3.5.5)
- predicates (11.3.1)
- prepositional phrase attachment ambiguity (7.3.1)
- prepositional phrase attachment ambiguity (7.4.1)
- Prepositional Phrase Attachment Corpus (7.3.1)
- present participle (3.3.1)
- Principle of Compositionality (11.1)
- probabilistic context free grammar (8.4.1)
- productions (7.4)
- proper nouns (3.2.2)
- propositional variables (11.2)
Q
R
- raw string (1.8)
- recognizing (8.2.2)
- record (5.2.3)
- record (12.2.1)
- recursion (7.4)
- recursion (7.4.2)
- recursive (7.4.2)
- reduce (7.5.2)
- reduce-reduce conflict (7.5.2)
- reentrancy (10.3.2)
- refactor (5.4.3)
- regular expression (1.8)
- regular expression operator (1.8)
- Relation Extraction (6.7)
- relational operators (1.6.2)
- representation (1.3.3)
- root (7.3.1)
- rules (8.3.1)
S
- satisfies (11.3.2)
- Scanner Rule (8.3.5)
- scope (7.3.1)
- scope (11.3.4)
- segmentation (6.1)
- self-loop edge (8.3)
- semantic (3.5.2)
- semi-structured data (6.7)
- sentence token (2.2)
- sentence type (2.2)
- sequence (1.5.5)
- set (1.7.3)
- shift (7.5.2)
- shift-reduce conflict (7.5.2)
- shift-reduce parser (7.5.2)
- Shoebox (12.2)
- sisters (7.3.3)
- slash categories (10.4.4)
- slice (1.4.2)
- sliding window (5.2.5)
- stack (5.2.4)
- standoff annotation (12.2.3)
- start-symbol (7.4.1)
- stem (2.3.2)
- strategy (8.3.1)
- string formatting expressions (1.5.3)
- string (1.3.1)
- structurally ambiguous (7.4.1)
- structure sharing (10.3.2)
- structured data (6.7)
- subcategories (7.4.3)
- Subject-Auxiliary Inversion (7.3.2)
- subscripting (1.4.1)
- substrings (1.4)
- subsumes (10.3.3)
- subsumption (10.3.3)
- subtype (10.6)
- suffix (2.3.2)
- synonyms (2.5.1)
- synsets (2.5)
- syntactic (3.5.2)
- syntax error (1.2.1)
T
- tag (10.3.2)
- tag pattern (6.3.1)
- tag set (3.1)
- tagged (3.1)
- tagging (3.1)
- terminals (7.4.1)
- terms (11.3.1)
- text (12.2.1)
- the principle of compositionality (11.4.1)
- token (2.2)
- tokenization (2.2)
- Toolbox (12.2)
- Top-Down Expand Rule (8.3.4)
- Top-Down Expand Rule (8.3.4)
- top-down (5.5.3)
- Top-Down Initialization Rule (8.3.4)
- Top-Down Initialization Rule (8.3.4)
- Top-Down Match Rule (8.3.4)
- Top-Down Match Rule (8.3.4)
- top-down parsing (7.5.1)
- Top-Down Strategy (8.3.4)
- training (3.5.3)
- transform-and-conquer (5.5)
- transitive (3.2.2)
- transitive verbs (7.4.3)
- tree diagram (7.3.1)
- tuple (3.2.1)
- tuples (1.8.1)
- Turing Test (13.1)
- type (2.2)
- type (2.2)
- type raising (11.4.3)
- Typed feature structures (10.6)
U
V
W
Z
Index
_
A
- A* Parser (8.4.2)
- A* parser (8.4.3)
- adjectives (3.5.1)
- adverbs (3.5.1)
- agreement (10.2.1)
- American National Corpus (12.2)
- appropriate (10.6)
- articles (3.5.1)
- artificial intelligence (1.1.2)
- assignment (1.3.2)
- Assignment (11.3.2)
- assigns (1.3.2)
- associative array (5.2.6)
- atomic (10.2.3)
- attribute value matrix (10.2.3)
- auxiliaries (10.4.3)
- auxiliary (10.2.3)
B
- backtracks (7.5.1)
- base (2.3.2)
- beam search (8.4.4)
- best-first search strategy (8.4.4)
- bigram (2.3.2)
- binary predicate (11.3.1)
- BIO Format (6.9)
- body (1.5.2)
- Boolean context (1.6.5)
- Boolean (1.6.2)
- boolean (10.2.3)
- bottom-up (5.5.3)
- Bottom-Up Initialization Rule (8.3.3)
- Bottom-Up Initialization Rule (8.3.3)
- bottom-up parsing (7.5.1)
- Bottom-Up Predict Rule (8.3.3)
- Bottom-Up Predict Rule (8.3.3)
- Bottom-Up Strategy (8.3.3)
- British National Corpus (12.2)
- business information analysis (1.1.2)
C
- call-by-value (5.4.2)
- call (1.4.1)
- call structure (5.5.3)
- cartesian product (5.2.5)
- Catalan numbers (8.1)
- characters (1.4)
- chart (8.2.2)
- chart parsing (8.2)
- chart parsing (8.2)
- child (7.3.3)
- CHILDES (12.2)
- chink (6.4.4)
- chink (6.9)
- chinking (6.4.4)
- chunker (6.3)
- chunking (6.1)
- chunks (6.1)
- closed class (3.5.2)
- closed formula (11.3.3)
- coindex (10.3.2)
- common nouns (3.2.2)
- complements (7.4.3)
- complete edge (8.3)
- complete (7.5.4)
- complete (8.4.4)
- complex (10.2.3)
- compound keys (5.2.6)
- computer science (1.1.2)
- concatenation (1.3.1)
- conditional expression (1.6.1)
- conditional frequency distribution (2.4.6)
- constituency (7.3.2)
- constituents (7.3.2)
- context-free grammar (7.4)
- control structure (1.5.2)
- control structure (1.6.1)
- conversion specifier (1.5.3)
- copy (5.2.1)
- corpus linguistics (1.1.2)
- Corpus Linguistics (2.4.2)
- count nouns (3.2.2)
- counters (1.7.2)
D
- data types (1.6.4)
- daughter (7.3.3)
- decorator (5.5.3)
- decrease-and-conquer (5.5)
- delimited (1.3.1)
- dependency grammar (7.4.4)
- derivation (7.4.5)
- determiners (3.5.1)
- diagnosis (6.8)
- dialogue (13.1)
- dictionary (1.7.1)
- direct recursion (7.4.2)
- directed acyclic graphs (10.3.2)
- divide-and-conquer (5.5)
- docstring (5.4)
- dot (8.3)
- dotted edges (8.3)
- Dublin Core (12.3.6)
- dynamic programming (8.2)
- dynamically typed (5.4.1)
E
F
- f-structure (10.6)
- feature (10.2.2)
- feature path (10.3.2)
- feature structure (10.2.3)
- fields (5.2.3)
- filler (10.4.4)
- first-in-first-out (5.2.4)
- format string (1.5.3)
- frequency distribution (2.4.1)
- function body (5.4)
- function (1.4.1)
- function (2.4.3)
- function (5.4)
- Fundamental Rule (8.3.2)
- Fundamental Rule (8.3.2)
G
H
I
- identifiers (1.3.3)
- immutable (1.5.1)
- immutable (5.2.3)
- immutable (5.2.6)
- import (1.5.4)
- incomplete edge (8.3)
- increment (1.5.2)
- index (1.4.1)
- indexing (1.4.1)
- indirect recursion (7.4.2)
- inference (13.1)
- inflected (2.3.2)
- Information Extraction (6.7)
- interpreter (1.2.1)
- intransitive (3.2.2)
- IOB tags (6.2.2)
- iteration (1.5.2)
K
L
- labeling (6.1)
- lambda expressions (5.4.5)
- Lancaster Stemmer (2.3.2)
- last-in-first-out (5.2.4)
- leaves (7.3.1)
- leaves (7.3.1)
- left-corner (7.5.3)
- left-corner parser (7.5.3)
- left recursive (7.4.2)
- lemma (2.3.2)
- lemma (2.3.2)
- Lemmatization (2.3.2)
- lexeme (2.3.2)
- lexical ambiguity (7.3.1)
- lexical categories (3.1)
- lexical productions (7.4.1)
- lexicon (12.2.1)
- licensed (10.4.4)
- licenses (7.4.1)
- linguistic category (10.2.3)
- List comprehensions (2.3.3)
- list (1.5.1)
- logical connectives (11.2)
- long-distance dependency (10.1)
- loop variable (1.5.2)
- lowest-cost-first search strategy (8.4.4)
M
- machine intelligence (13.1)
- majority class classifier (3.2.4)
- map (1.7)
- mass nouns (3.2.2)
- matches (1.8)
- maximal projection (10.4.2)
- memoization (5.5.3)
- method (I.5)
- methods (1.5.1)
- modals (3.5.1)
- model (11.1)
- module (1.5.4)
- morpho-syntactic (3.3.1)
- morphological (3.5.2)
- most likely constituents table (8.4.2)
- mutable (1.5.1)
- mutable (5.2.3)
- mutual information (2.4.7)
N
O
P
- parent (7.3.3)
- parse edge (8.3)
- parser (7.5)
- part-of-speech tagging (3.1)
- part-of-speech tags (3.1)
- partial information (10.3.3)
- partial parsing (6.2.1)
- parts of speech (3.1)
- past participle (3.3.1)
- personal pronouns (3.5.1)
- phrasal level (10.4.2)
- phrase structure (7.2)
- polysemous (2.5.1)
- Porter Stemmer (2.3.2)
- POS-tagging (3.1)
- POS tags (3.1)
- pre-sort (5.5)
- pre-terminals (7.4.1)
- precision/recall trade-off (3.5.5)
- predicates (11.3.1)
- prepositional phrase attachment ambiguity (7.3.1)
- prepositional phrase attachment ambiguity (7.4.1)
- Prepositional Phrase Attachment Corpus (7.3.1)
- present participle (3.3.1)
- Principle of Compositionality (11.1)
- probabilistic context free grammar (8.4.1)
- productions (7.4)
- proper nouns (3.2.2)
- propositional variables (11.2)
Q
R
- raw string (1.8)
- recognizing (8.2.2)
- record (5.2.3)
- record (12.2.1)
- recursion (7.4)
- recursion (7.4.2)
- recursive (7.4.2)
- reduce (7.5.2)
- reduce-reduce conflict (7.5.2)
- reentrancy (10.3.2)
- refactor (5.4.3)
- regular expression (1.8)
- regular expression operator (1.8)
- Relation Extraction (6.7)
- relational operators (1.6.2)
- representation (1.3.3)
- root (7.3.1)
- rules (8.3.1)
S
- satisfies (11.3.2)
- Scanner Rule (8.3.5)
- scope (7.3.1)
- scope (11.3.4)
- segmentation (6.1)
- self-loop edge (8.3)
- semantic (3.5.2)
- semi-structured data (6.7)
- sentence token (2.2)
- sentence type (2.2)
- sequence (1.5.5)
- set (1.7.3)
- shift (7.5.2)
- shift-reduce conflict (7.5.2)
- shift-reduce parser (7.5.2)
- Shoebox (12.2)
- sisters (7.3.3)
- slash categories (10.4.4)
- slice (1.4.2)
- sliding window (5.2.5)
- stack (5.2.4)
- standoff annotation (12.2.3)
- start-symbol (7.4.1)
- stem (2.3.2)
- strategy (8.3.1)
- string formatting expressions (1.5.3)
- string (1.3.1)
- structurally ambiguous (7.4.1)
- structure sharing (10.3.2)
- structured data (6.7)
- subcategories (7.4.3)
- Subject-Auxiliary Inversion (7.3.2)
- subscripting (1.4.1)
- substrings (1.4)
- subsumes (10.3.3)
- subsumption (10.3.3)
- subtype (10.6)
- suffix (2.3.2)
- synonyms (2.5.1)
- synsets (2.5)
- syntactic (3.5.2)
- syntax error (1.2.1)
T
- tag (10.3.2)
- tag pattern (6.3.1)
- tag set (3.1)
- tagged (3.1)
- tagging (3.1)
- terminals (7.4.1)
- terms (11.3.1)
- text (12.2.1)
- the principle of compositionality (11.4.1)
- token (2.2)
- tokenization (2.2)
- Toolbox (12.2)
- Top-Down Expand Rule (8.3.4)
- Top-Down Expand Rule (8.3.4)
- top-down (5.5.3)
- Top-Down Initialization Rule (8.3.4)
- Top-Down Initialization Rule (8.3.4)
- Top-Down Match Rule (8.3.4)
- Top-Down Match Rule (8.3.4)
- top-down parsing (7.5.1)
- Top-Down Strategy (8.3.4)
- training (3.5.3)
- transform-and-conquer (5.5)
- transitive (3.2.2)
- transitive verbs (7.4.3)
- tree diagram (7.3.1)
- tuple (3.2.1)
- tuples (1.8.1)
- Turing Test (13.1)
- type (2.2)
- type (2.2)
- type raising (11.4.3)
- Typed feature structures (10.6)
U
V
W
Z
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is