Description: Define the set of
retractions on two topological spaces. We say that
 is a
retraction from is a
retraction from  to to
 . or . or     Retr Retr   iff
there is an iff
there is an  such that
such that    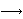  
   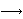  are continuous
functions called the retraction and section respectively, and their
composite are continuous
functions called the retraction and section respectively, and their
composite  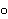  is homotopic to the identity map. If a
retraction
exists, we say is homotopic to the identity map. If a
retraction
exists, we say  is a retract of
is a retract of  .
(This terminology is
borrowed from HoTT and appears to be nonstandard, although it has
similaries to the concept of retract in the category of topological
spaces and to a deformation retract in general topology.) Two
topological spaces that are retracts of each other are called homotopy
equivalent. (Contributed by Mario Carneiro,
11-Feb-2015.) .
(This terminology is
borrowed from HoTT and appears to be nonstandard, although it has
similaries to the concept of retract in the category of topological
spaces and to a deformation retract in general topology.) Two
topological spaces that are retracts of each other are called homotopy
equivalent. (Contributed by Mario Carneiro,
11-Feb-2015.) |