On Integrating Catalogs

Rakesh Agrawal   and   Ramakrishnan Srikant

IBM Almaden Research Center
650 Harry Road
San Jose, CA 95120, USA

 

Copyright is held by the author/owner(s).

WWW10, May 1-5, 2001, Hong Kong.

ACM 1-58113-348-0/01/0005.

 

Note: We strongly recommend printing the PDF version of this paper.

Abstract:

We address the problem of integrating documents from different sources into a master catalog. This problem is pervasive in web marketplaces and portals. Current technology for automating this process consists of building a classifier that uses the categorization of documents in the master catalog to construct a model for predicting the category of unknown documents. Our key insight is that many of the data sources have their own categorization, and classification accuracy can be improved by factoring in the implicit information in these source categorizations. We show how a Naive Bayes classification can be enhanced to incorporate the similarity information present in source catalogs. Our analysis and empirical evaluation show substantial improvement in the accuracy of catalog integration.

Keywords: Classification, Categorization, Data Mining, Catalog Integration, Web Portals, Web Marketplaces

1. Introduction

Imagine you are a marketplace for electronic components. Your catalog features nearly ten million parts categorized into 5000 categories. Noticing your success, a major distributor wants to join your marketplace. This distributor's catalog contains nearly a million parts categorized into 2000 categories. Your problem is how to quickly integrate this distributor's catalog into your catalog.

This problem is pervasive on the web, given many websites are aggregators of information from various sources. B2C shops like Amazon need to integrate catalogs from multiple vendors. B2B portals, Chipcenter and Questlink, each with a large catalog of their own, recently merged to form eChips. Information portals like Yahoo! and Google categorize documents into categories. One can easily conceive a web service that combines the two portals. Many corporate portals are now merging intra-company and external information into a uniform categorization.

This paper presents a new technique to help automate the task of catalog integration. Let us call your marketplace MrCurrent and the distributor who wants to join you MrNew. A straightforward approach to attacking the catalog integration problem would be to formulate it as a classification problem [Mit97]. Take the MrCurrent catalog, treat each category in the catalog as a class, and the information about the products belonging to each category as training examples for the corresponding class. We thus have a well-posed classification problem and a training set and we can build a predictive model for classifying MrNew's products into MrCurrent's categories.

Notice, however, in this straightforward approach, we completely ignored MrNew's categorization. On the other hand, MrNew's categorization contains valuable implicit information about product similarity. Suppose the classifier's prediction is such that 98% of the products belonging to some category in MrNew's catalog fall in one category in MrCurrent's catalog and 2% in a different category. Those 2% predictions are quite possibly errors, but it will also be a mistake to take a winner-takes-all attitude and assume that those 2% are necessarily errors.

Our key contribution is how to incorporate the implicit information contained in MrNew's catalog into the classification process. We show that this additional information can substantially boost classification accuracy.

1.1 Problem Statement

We now formally define the catalog integration problem we are solving.

A document d is an object consisting of i) a set of words, and/or ii) a set of attribute value pairs. By including attribute value pairs, we are able to cover both text documents as well as product descriptions.

A catalog is a partitioning of a set of documents into a set of categories¹. We are given two catalogs:

• A master catalog M with a set of categories $C_1, C_2, \ldots, C_n$and a set of documents in each category.
• A source catalog N with a set of categories $S_1, S_2, \ldots, S_m$and another set of documents.

We need to find the category in M for each document in N.

We optionally identify documents in N that do not fit well in M and give the user the option of adding these as new categories in M.

1.2 Limitations

An assumption underlying our model is that the categorizations used by catalogs M and N are homogenous and have significant overlap. It is possible that the categorizations used by M and N may be completely orthogonal to each other. For instance, consider a corpus of documents describing businesses. The categorization in M is by business type, whereas the categorization in N is by geographical location. In such cases, the implicit information in N will not help us better categorize the documents into M.

Vocabulary changes are a problem for classification in general. For instance, it was observed in [Lar99] that patents about similar inventions can contain very different terminology. If the vocabulary in N is quite different from M, the classification accuracy will certainly be affected. However, this problem is orthogonal to the idea of using the similarity information in N.

Our model flattens the catalog hierarchy and treats it as a set of categories. Past studies [DC00] [CDAR97] have shown that exploiting the hierarchical structure can lead to better classification results than using the flattened structure. Our enhancements for using the information in N can be easily incorporated in a Naive Bayes hierarchical classifier, such as one used in [CDAR97]. Incorporation of these enhancements into other classification schemes, such as the SVM classifier used in [DC00], requires further work.

Another issue related to hierarchies is that the hierarchy in M may be more detailed than N or vice-versa. If M is more detailed than N, our technique can still be helpful. For example, if N has a category ``Cars'', while M has ``Sports Cars'' and ``Sedans'', our technique will not help distinguish between ``Sports Cars'' and ``Sedans''. However, it will help distinguish between these two categories and say ``Trucks''. On the other hand, if N is more detailed than M, the detailed categories in N can be first merged into a super category and our technique can then be applied. (While our technique would be effective even if applied without merging the detailed categories, we show in Section 5.2 that having more documents in the categories in N leads to better results.)

1.3 Related Work

Inducing classification model for a set of categories given examples of objects for each category is a much studied topic in the statistics, machine learning, and data mining literature. See, for instance, [Mit97] for a comprehensive review of various classification techniques. Naive-Bayes classifiers [Goo65] are competitive with other techniques in accuracy [CDAR97] [LR94] [Lan95] [PB97] [MN98]. They are also fast: building the model requires only a single pass over the documents and they quickly classify new documents. Our proposed solution is also Bayesian.

The observation that the classification techniques can be used to assign documents to a hierarchy has been previously made in connection with folder systems. Proposals on the development of classification models for the purpose of routing e-mail include [ABS00] [Coh96] [SDHH98] [SK99]. Other systems provide agents that assist e-mail users by predicting an action the user is likely to take [Mae94] [PE97]. SONIA [SYB98] uses agglomerative text clustering to organize the results of queries to networked information sources, and Naive Bayes classification to organize new documents within an existing categorization scheme. Text classification has also been applied in other domains, e.g. [DPBA99] showed how well SEC (Security Exchange Commission) filings can be classified into SIC categories. None of these systems address the task of merging hierarchies.

The Athena system [ABS00] includes the facility of reorganizing a folder hierarchy into a new hierarchy. The user provides examples of documents for every node of the new hierarchy, which is used as the training set for learning the classification model for new hierarchy. The documents from old hierarchy are then routed to the new hierarchy using this model. But no information from the old hierarchy is used in either building the model or routing the documents.

1.4 Paper Organization

The rest of the paper is organized as follows. In Section 2, we review Naive Bayes classification and give the basic algorithm that applies this technique in a straightforward manner to merge documents from a source catalog into an existing catalog. In Section 3, we present our enhanced algorithm that uses the implicit information in the source catalog to improve the accuracy of catalog integration. We present an analysis in Section 4 that shows why using implicit information is a win. We present an empirical evaluation in Section 5 that gives improvements in accuracy realized in our experiments. We conclude with a summary in Section 6.

   
2. Straightforward Approach to Catalog Integration

We start with a quick review of Naive Bayes classification and then give the basic algorithm that applies this technique for merging catalogs in a straightforward manner.

2.1 Naive Bayes Classification

The Naive Bayes classifier estimates the posterior probability of category C_i given a document d via Bayes' rule [Mit97]:

$$\Pr(C_i \,\vert\,d) = \frac{ \Pr(C_i) \Pr(d \,\vert\,C_i) }{ \Pr(d) }$$ (1)

We can ignore $\Pr(d)$ since it is the same for all categories and we need only the relative probability of the categories to determine d's category assignment. $\Pr(C_i)$ is estimated by

$$\Pr(C_i) = \frac{ \mbox{Number of documents in category $C_i$ } } { \mbox{Total number of documents in the dataset} }$$ (2)

which is easy to compute.

We treat $\Pr(d \,\vert\,C_i)$ as an input in our enhanced algorithm. We review here how to compute $\Pr(d \,\vert\,C_i)$ only for the case of text, and refer readers to [Mit97] for extensions to the case when the document also contains a set of attribute-value pairs.²

To estimate the first term on the right hand side of Eq. 3, assume that the words in d are independent of each other. We get

$$\Pr(d \,\vert\,C_i) = \prod_{t \in d} \Pr(t \,\vert\,C_i)$$ (3)

where t represents the words (tokens). To estimate $\Pr(t \,\vert\, C_i)$, we compute the frequency of occurrence of every word appearing in any of the textual descriptions of the set of documents in category C_i. Let n(C_i,t) be the number of occurrences of word t in documents in category C_i(counting multiple occurrences), and $n(C_i) = \sum_t n(C_i,t)$ the total number of words in documents in category C_i. Then the maximum likelihood estimate for $\Pr(t \,\vert\, C_i)$ is simply n(C_i,t) / n(C_i). However, using this estimate would give a probability of zero for any word that does not occur in any of the documents in the category, and thus result in $\Pr(d \,\vert\,C_i)$ being zero for any document dthat contained a word not present in category C_i. Following [ABS00], we address this problem by using Lidstone's law of succession to smooth the maximum likelihood estimate. For $\lambda \geq 0$, we estimate $\Pr(t \,\vert\, C_i)$ to be

$$\Pr(t \,\vert\,C_i) = \frac{n(C_i,t) + \lambda}{n(C_i) + \lambda \vert V\vert}$$ (4)

where |V| is the size of the vocabulary (i.e., the number of distinct words in the textual descriptions in all of the documents). The above estimate is a linear interpolation of the maximum likelihood estimate n(C_i,t)/n(C_i) and the uniform prior 1/|V|. The optimal value of $\lambda$ is computed by using a randomly selected subset of documents in M as a validation set, i.e., we build the classification model using the rest of M, and compute the accuracy of the model for different values of $\lambda$ on the validation set.

2.2 Basic Algorithm

Figure 1 presents the basic method that uses the standard Naive Bayes technique. We first build a classification model using the set of documents already in M. This classification model is then used to place documents from N into M.

  

1. For each category Ci in M, compute $\Pr(C_i)$ and $\Pr(t \,\vert\,C_i)$
       (Eqs. 2 and 4, respectively).
2. For each category S in N:
       For each document d in S:
           (a) Compute $\Pr(C_i \,\vert\,d)$ for each category Ci in M using 
               the statistics computed in Step 1 (Eqs. 1 and  3).
           (b) Assign d to the category with the highest value
               for $\Pr(C_i \,\vert\,d)$.

Figure 1: Basic Algorithm

Note that depending on policy parameters:

• A document d may be assigned to more than one category (say C_iand C_j) if $\Pr(C_i \vert d)$ and $\Pr(C_j \vert d)$ both have high values.
• If for some document d, the value of $\Pr(C_i \vert d)$ is low for all the categories, d may be kept aside for manual classification, possibly into a new category of M.
• If for some category S in N, a large fraction of the documents satisfy the previous condition, S may be flagged as a candidate for becoming a new category of M.

Our main focus in this paper is on boosting the classification accuracy by incorporating the implicit information present in N. For ease of exposition, therefore, we assume in the remainder of the paper that each document in N is assigned to exactly one category in M.

   
3. Enhanced Algorithm

Our proposed method uses the similarity information implicit in the categorization of documents in N to build more accurate classification models. The intuition is that if two documents belong to the same category in N, they are more likely to belong to the same category in M.

Let S denote a category in N. We can extend Bayes rule from Eq. 1 to incorporate the implicit information in S. We will use the standard notation $\Pr(x,y)$ to refer to $\Pr(x \mbox{ and } y)$. We also use $\Pr(S)$ to refer to $\Pr(d \in S)$, and $\Pr(C_i)$ to refer to $\Pr(d \in C_i)$. The posterior probability of category C_i in M given a document d belonging to category S in N is computed as:

 

$${ \Pr(C_i \,\vert\,d,S) }$$

$$\frac{ \Pr(C_i,d,S) }{ \Pr(d,S) }$$ =

$$\frac{ \Pr(C_i) \Pr(S,d \,\vert\,C_i) }{ \Pr(d,S) }$$ =

$$\frac{ \Pr(C_i) \Pr(S \,\vert\,C_i) \Pr(d \,\vert\,C_i) } { \Pr(S, d) }$$ =

$$\mbox{~~~~~assuming $d$ , $S$\space are independent given $C_i$ }$$

$$\frac{ \Pr(S) \Pr(C_i \,\vert\,S) \Pr(d \,\vert\,C_i) } { \Pr(S, d) }$$ =

$$\mbox{~~~~~since $\Pr(C_i \,\vert\,S) \Pr(S) = \Pr(S \,\vert\,C_i) \Pr(C_i)$ }$$

$$\frac{ \Pr(C_i \,\vert\,S) \Pr(d \,\vert\,C_i) } { \Pr(d \,\vert\,S) }$$ = (5)

Eq. 5 is similar to Eq. 1, except that we have $\Pr(C_i \,\vert\,S)$ instead of $\Pr(C_i)$. (We also have $\Pr(d \,\vert\,S)$ instead of $\Pr(d)$ in the denominator, but since this term is the same for all classes, it does not affect relative probabilities.)

To estimate $\Pr(C_i \,\vert\,S)$, we first classify the documents using the basic algorithm, then use the categories of the documents in S to compute the estimate. A simple estimate could be:

$$\Pr(C_i \,\vert\,S) = \frac { \mbox{Number of documents in $... ... be in $C_i$ } } { \mbox{Total number of documents in $S$ } }$$

However, while this equation is identical in form to the estimate for $\Pr(C_i)$(Eq. 2), that equation was based on real frequencies, while this equation is based on estimated frequencies. The accuracy of the estimate depends on the accuracy of the classifier.

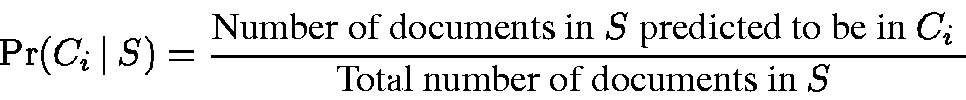
As an illustration, consider a scenario where we know that the source catalog categories are identical to the master catalog categories. With a perfect classifier, the above estimate will be 1 for the true category and 0 for all other categories. With a classifier that is 90% accurate, the estimate will be .9 for the true category, and perhaps .1/kfor k other categories assuming the errors are evenly split among them. In this case, we would like $\Pr(C_i \,\vert\,S)$ to be 1 for the category with the most number of documents, and 0 for the other categories, i.e., use the majority rule. More generally, we can use an index $w \geq 0$ that reflects the similarity between the categorization of the two catalogs to decide the amount of weight to give to the implicit information. We would also like to smooth our estimate using the statistics for $\Pr(C_i)$ from M, and have the property that for w = 0, our enhanced classifier defaults to the standard classifier. A formula that satisfies these goals is:

 

$${ \Pr(C_i \,\vert\,S) = }$$

$$\frac { \vert C_i\vert \times (\mbox{Number of docs in $S$\space ... ... C_j\vert \times (\mbox{Number of docs in $S$ predicted to be in $C_j$ })^w ) }$$

where |C_i| is the number of documents in category C_i in M. For w = 0, $\Pr(C_i \,\vert\,S) = \vert C_i\vert \times B_i / \sum_j (\vert C_j\vert \times B_j)$, where B_i is 1 if at least one of the documents in Swas predicted to be in category C_i, and 0 otherwise. Notice that even though the absolute probabilities are different, the relative probabilities among the set of classes that the standard classifier predicted for any of the documents in S is the same. Hence the prediction of the enhanced classifier will be the same as the prediction of the standard classifier when w = 0.

Figure 2 describes the enhanced algorithm, for a given weight w.

  

1.  For each category Ci in M, compute $\Pr(C_i)$ and $\Pr(t \,\vert\,C_i)$
    (Eqs. 2 and 4, respectively).
2.  For each category S in N:
    (a) For each document d in S:
        (i) Compute $\Pr(C_i \,\vert\,d)$ for each category Ci in M
             using the basic algorithm (Figure 1).
        (ii) Tentatively assign d to the category with the
             highest value for $\Pr(C_i \,\vert\,d)$.
    (b) Use the results of Step 2(a)(ii) and Eq. 6 to compute $\Pr(C_i \,\vert\,S)$.
    (c) Re-classify each document in S using $\Pr(C_i \,\vert\,S)$ instead
         of $\Pr(C_i)$ in the classification model ${\cal C}$ (Eq. 5).

Figure 2: Enhanced Algorithm

3.1 Determining Weight

Before describing the method for selecting weight w, we first motivate the need for selecting a good value for w.

Example Consider a master catalog M in which there are separate categories for ``Digital Cameras'' and ``Computer Peripherals''. When we integrate products from the source catalog N, let the basic algorithm come up with the following probabilities for the five products in one of the categories in N.

	Peripherals	Camera
P1	.1	.9
P2	.2	.8
P3	.2	.8
P4	.2	.8
P5	.9	.1

Based on these probabilities, four out of the five products belong to Camera and one to Peripherals. In the master catalog, let there be 10 products each of these two categories, and none in any other category (to simplify the example). With a weight of 1, $\Pr(\mbox{Camera} \,\vert\,S)$ = 4*10/(4*10+1*10) = 0.8 and $\Pr(\mbox{Peripherals} \,\vert\,S)$ = 1*10/(4*10 +1*10) = 0.2. After incorporating these probabilities (and normalizing), the enhanced algorithm would assign:

	Peripherals	Camera
P1	.03	.97
P2	.06	.94
P3	.06	.94
P4	.06	.94
P5	.69	.31

With a weight of 2, $\Pr(\mbox{Camera} \,\vert\,S)$ = 16*10/(16*10+1*10) = 0.94 and $\Pr(\mbox{Peripherals} \,\vert\,S)$ = 1*10/(16*10+1*10) = 0.06. This would result in:

	Peripherals	Camera
P1	.01	.99
P2	.02	.98
P3	.02	.98
P4	.02	.98
P5	.36	.64

Thus the classification of P5 does not change with a weight of 1, but switches to the majority category with a weight of 2.

3.1.1 Method

To determine a good value for the weight, we need a tune set of documents in N for which we know the correct categorization with respect to M. If there are some common documents between M and N, we can use these common documents as the tune set. If there are no common documents between the two catalogs, the creation of the tune set requires user interaction. We select a random subset of the documents in N, and present these to the user to get their categorization in M.

We first make one pass through step 2(a) in Figure 2 for all the documents in N, allowing us to compute $\Pr(C_i \,\vert\,S)$ for a given weight w. Next, for each document in the tune set, for a set of values for w, we go through steps 2(b) and 2(c) in Figure 2 and determine the values of w for which the document is correctly classified. We typically use an exponentially increasing series for the set of possible values of w, e.g. (0, 1, 3, 10, 30, 100, 300, 1000). We then select the weight that gives the highest accuracy on the documents in the tune set. If a set of weights give the same accuracy, we break the tie by choosing the smallest weight, and thus not overweight the similarity implied by the hierarchy N.

We can reduce the number of documents the user has to inspect by making two passes. After selecting a random subset of documents in N, we make a first pass through Step 2 for those documents, and discard those which have the same categorization for all the weights. Since the categorization does not change, knowing the true category for these documents will not help us choose the weight. We then present the remaining documents to the user, and choose the weight that gives the highest accuracy on these documents. We empirically found in Section 5.2 that by following this strategy, feedback from the user on just 5 to 10 documents was sufficient to get a near-optimal value for the weight.

Depending on the cost of getting a tune set and the size of the catalog, we either choose a global weight for the entire catalog, or tune weights differently for different sections of the catalog.

   
4. Analysis

We first study the behavior of the enhanced algorithm with respect to weight w. We then show that with a good choice for the value of w, the enhanced algorithm will do no worse, and can do substantially better than the basic algorithm.

4.1 Effect of Weight on Accuracy

Consider the documents belonging to a category S in N. Our first theorem shows that as we increase the weight w, the predicted category of a document in S will either stay the same or switch from a less frequent category to a more frequent category, where frequency of a category is the number of documents in S predicted to be in that category. Denote

$$f_x := \mbox{Number of documents from $S$\space predicted to be in $C_x$ }$$

Theorem 1   For any pair of weights $w_1, w_2 \geq 0$, let w₁ > w₂, let C_x1 be the predicted category of document d at weight w₁, and C_x2 the predicted category at weight w₂. Then $f_{x_1} \geq f_{x_2}$.

Proof: See Appendix A. $\Box$

Let $C_{x_1}, C_{x_2}, \ldots, C_{x_n}$ represent the categories ordered by their frequency in the predicted categories of the documents in S, i.e., $f_{x_1} \geq f_{x_2} \geq \ldots \geq f_{x_n}$, Figure 3 shows the movement of documents with increasing weight. We can split the documents into three classes:

1. Benefit: Those to the right of the X's that can move to the X's.

2. At Risk: Those currently in the X's that might move to the left of the X's.

3. Lost Cause: Those to the left of the X's.

As we increase w, documents will move from the first class to the second, and from the second to the third. If more documents move from 1 to 2 than move from 2 to 3, accuracy will increase. On the other hand, if more documents move from from 2 to 3 than move from 1 to 2, accuracy will drop.

  

Figure 3: Movement of Documents

4.2 Superiority of the Enhanced Algorithm

Theorem 2   For each document d, there either exists a single interval $(w_1, w_2), 0 \leq w_1 \leq w_2$ in which the document will be correctly classified, or the document will never be correctly classified.

Proof: See Appendix A. $\Box$

Lemma 1   Given a set of documents, there exists a set of intervals $(w_{1l}, w_{1g}), (w_{2l}, w_{2g}), \ldots, (w_{nl}, w_{ng})$ for the weight such that the number of correctly classified documents is highest in these intervals.

Theorem 3   The highest possible accuracy achievable with the enhanced algorithm is no worse than what can be achieved with the basic algorithm.

Proof: Basic algorithm is the special case of the enhanced algorithm for weight 0. $\Box$

The catch is that the optimum value of the weight for which the enhanced algorithm achieves highest accuracy is data dependent. The method using a tune set described in the previous section attempts to select a good value for the weight, but there is no guarantee of success. Our experimental results in the next section show that we were able to get substantial accuracy improvements using this method.

   
5. Experimental Results

We present experimental results using two types of datasets:

Synthetic Catalogs Start with a real-world catalog and consider it to be the master catalog M. Derive source catalogs N from M using various distributions. Consider a specific category C_m in M. Some of the documents from C_mare assigned to the corresponding category in N, while some are spread over other categories. Use a distribution to determine how many documents are distributed over how many categories. For example, a simple 80-20 distribution will send 80% of the documents to the corresponding category and 20% to some other category. Different distributions result in different degrees of overlap between M and N. We use a variety ranging from a ``perfect'' match between the two catalogs, to a ``Gaussian'' distribution where there is only a moderate amount of similarity. We generate synthetic catalogs from three master catalogs: a collection of news articles from Reuters, the Pangea electronics part descriptions dataset, and a slice of the Google hierarchy.

Now consider a specific document d from C_m in M that the synthetic data generation assigns to the category S_n in N. While integrating N into M, if d is assigned a category other than C_m, we count it as a classification error; otherwise the assignment is correct.

Real Catalogs Start with two real-world catalogs that have some common documents. Treat the first catalog minus the common documents as the master catalog M. Remove from the second catalog all documents except the common ones. Treat the remaining documents in the second catalog as the source catalog N. We thus know for each document in N the correct classification in M. The goal for the catalog integration algorithm now is to successfully predict for each document in N its correct category in M. We do these experiments using Google and Yahoo! categories.

Experiments Our goal is to understand the following performance characteristics:

• Accuracy advantage of the enhanced algorithm over the basic algorithm.
• The effect of weight on the accuracy of the enhanced algorithm.
• The size of tune set needed for the enhanced algorithm.
• The effect of the number of documents per category in the source catalog on the classification accuracy.

We use the classification accuracy as the metric for measuring the success of our approach. Accuracy is defined as

$$\frac{\mbox{Number of documents in {\em N}that are correctly classified}} {\mbox{Total number of documents in {\em N}}}$$

In the rest of this section, we describe in detail the datasets and the experimental results. Section 5.1 discusses the synthetic datasets and Section 5.2 the results with these datasets. Section 5.3 discusses the real datasets, and Section 5.4 reports results with these datasets.

   
5.1 Synthetic Catalogs

Master Catalogs We used the following master catalogs for generating synthetic catalogs:

• Reuters: This is a collection of news articles, and a popular benchmark in the information retrieval community. We used the version of Distribution 1.0 of Reuters-21578 in which each document is assigned a single category (available from http://www.research.att.com/ lewis).
• Pangea: This is a dataset of electronic component descriptions used in building the experimental B2B Pangea portal at IBM Almaden.
• Google.Outdoors: This is the set of web pages in the ``Recreation/Outdoors'' category in Google (available from http:// directory.google.com/Top/Recreation/Outdoors/). For each category in ``Outdoors'', we got the links both on the category page, and from each of the subcategories, and merged the set of links.

Figure 4 shows the number of categories and total number of documents for these catalogs.

  

Dataset	Categories	Docs
Reuters	82	11,367
Pangea	1148	37,012
Google.Outdoors	38	7,431

Figure 4: Dataset Characteristics: Reuters, Pangea & Google.Outdoors

Target Distributions for Synthetic Catalogs

Our synthetic catalogs have as many categories as the master catalog. We spread documents from a certain category in the master catalog to multiple categories in the synthetic catalog. Figure 5 shows the various target distributions we used for spreading documents. For the Perfect distribution, each category in the synthetic catalog will have documents from a single category in the master catalog. On the other hand, for GaussianB distribution, documents from a category in the master catalog will be spread over 7 categories in the synthetic catalog, and each category in the synthetic catalog will include documents from 7 categories in the master catalog. The intent was to evaluate the performance of our approach to catalog merging over a wide range of similarity characteristics between the categorizations of the two catalogs.

  

Name	Distribution
Perfect	100
90-10	90, 10
80-20	80, 20
GaussianA	68.2, 27.2, 4.3, 0.3
GaussianB	38.3, 29.9, 18.4, 8.8, 3.4, 0.9, 0.3

Figure 5: Target Distributions for Synthetic Catalogs

Figure 6 gives the details of the algorithm for generating N.

  

// n: number of categories in M
// $f_1, f_2, \ldots, f_m$:
cumulative frequency distribution 
// f0 := 0 (to simplify the description) 
for i := 1 to n begin 
    foreach document d in Ci begin 
        Let r := uniformly distributed random number in [0, 1). 
        Find p such that $f_p \leq r < f_{p+1}$.
        j := $(i+p) \mbox{ modulo } n$;
        Assign d to category Sj. 
    end 
end

Figure 6: Generating Synthetic Catalog

Figure 7 shows the actual distributions for the synthetic catalogs. These are slightly different from the target distributions because of the skew in category sizes of the master catalogs.

  

Distribution	Reuters	Pangea	Google
Perfect	100	100	100
90-10	91.2, 8.8	90.6, 9.4	91.1, 8.9
80-20	82.0, 18.0	80.9, 19.1	82.6, 17.4
GaussianA	70.8, 25.5, 3.5, 0.2	69.2, 27.1, 3.5, 0.1	68.5, 28.0, 3.4, 0.1
GaussianB	51.2, 27.5, 11.8, 6.5, 2.1, 0.9	45.2, 28.4, 15.8, 8.1, 2.2, 0.3	42.2, 28.8, 18.9, 7.2, 2.5, 0.3

Figure 7: Actual Distributions: Reuters, Pangea & Google.Outdoors

   
5.2 Experiments with Synthetic Catalogs

5.2.1 Effect of Weight on Accuracy

Figure 8 shows that the enhanced algorithm can substantially outperform the basic algorithm. The graphs show the accuracy for each of the source catalogs as we change the weight; the ``Base'' line is the accuracy of the basic algorithm. The accuracy numbers were computed using 10-fold cross-validation, i.e., we randomly partition the data into 10 sets, and for each set, train on the remaining 9 sets, and test on this set [BFOS84]. With a ``Perfect'' second catalog, the absolute increase in accuracy (at the best weight) is 12% for Reuters, 20% for Pangea and 29% for Google; the number of errors drops by 85% for Reuters, 73% for Pangea, and 65% for Google. With a distribution like GaussianA that results in considerable mismatch between the source and master catalogs, we still get an absolute increase of 5% for Reuters, 12% for Pangea and 15% for Google; the number of errors drops by 39% for Reuters, 43% for Pangea and 33% for Google. Notice that for distributions (for generating source catalogs) that are not a good match to the main catalog, very high weights can cause the enhanced algorithm to under-perform the basic classifier. Of course, once we use a tune set, we will avoid those weights.

  

(a) Reuters

(b) Pangea

(c) Google.Outdoors

Figure 8: Accuracy vs. Weight

In general, the optimal value of weight increases with increasing similarity between the two hierarchies. The other factor is the size of the documents in the dataset: as documents become longer, the differences between $\Pr(d \,\vert\,C_i)$ for different categories becomes larger and hence a higher weight is needed to influence the results. The documents from the Google dataset are significantly longer than those from Reuters or Pangea; hence for the same distribution of the synthetic hierarchy, the optimal weight is higher for Google.

5.2.2 Tune Set Size

To select the tune set, we first make one pass with the base classifier to get the prediction for each document, enabling us to compute $\Pr(C_i \,\vert\,S)$. (We reuse the computation, so this does not increase execution time.) We then select a random document, and check whether the enhanced classifier classifies it differently based on the weight. If so, we add it to the tune set; else we pick another document.

  

(a) Reuters

(b) Pangea

(c) Google.Outdoors

Figure 9: Accuracy vs. Tune Set Size

Figure 9 shows that very small tune sets are sufficient to choose the right weight. With just 5 carefully chosen examples, we are able to do almost as well as with 10 to 50 examples: there are only slight improvements beyond 10 examples. The reason why so few examples are sufficient is that changes in weights only change the classification of a small fraction (typically around 10%) of the total documents to be classified. By choosing only such documents to present for tuning, we get the same effect as we would by presenting 10 times as many random documents.

5.2.3 Catalog Size

Figure 10 shows the effect on accuracy as we increase the number of documents in the second catalog. The x-axis shows the weighted median category size, i.e., if the category size is 10 documents, half the documents are in categories (in the second catalog) with 10 or fewer documents, and half the documents are in categories with 10 more documents. (The median was averaged over the different test sets; hence it is not an integer.) We used a modified version of 5-fold cross-validation: the training set was always 80% of the data, but the test set ranged from 20% of the data to samples of that 20%. The weight was determined using a tune set of 10 documents (selected from the entire 20% in order not to affect the results). With small category sizes, our estimates of $\Pr(C_i \,\vert\,S)$ are likely to be off by quite a bit from the true value; hence it is not surprising that the accuracy increases with the category size. However, note that for Pangea and Google, we still get a substantial part of the accuracy boost even with median category sizes of just over 5 documents.

  

(a) Reuters

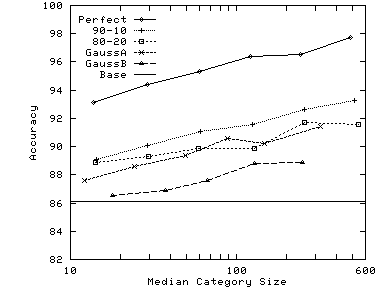(b) Pangea

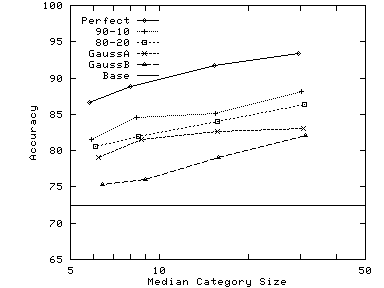(c) Google.Outdoors

Figure 10: Accuracy vs. Median Size of Categories in Synthetic Catalog

   
5.3 Real Catalogs

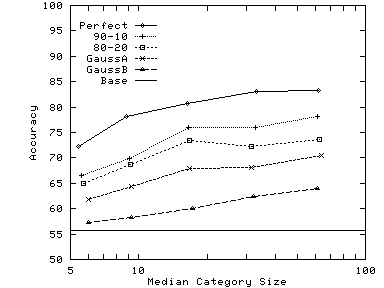To evaluate our approach using real catalogs for N, we wrapped the Google and Yahoo! websites, extracted over 100,000 links from 5 different sections of their categorizations, and retrieved the corresponding web pages.³ Incidently, we found less than 10% overlap between the links in Google and Yahoo!. Figure 11(a) shows the number of categories, number of links obtained from the website, and number of documents (after dropping the common documents and those documents our crawler could not get). When computing the set of common links, we ignored links that had multiple categories. Figure 11(b) shows similar numbers for the set of common documents. We include both the weighted median and the average documents per category, since the median can sometimes be much higher. This figure also shows the distributions of the categories. For instance, a single category in Google.Autos had, on average, 78% of documents from a single category in Yahoo.Autos, 9% from a second category in Yahoo.Autos, 5% from a third category, and so on. These distributions look similar to the Gaussian distributions we used in the synthetic catalogs, except that the tails are longer.

  

	(a) All Documents			(b) Common Documents
						Docs/Category
Dataset	Categories	Links	Docs	Categories	Docs	Average	Median	Distribution
Google.Autos	26	8095	7351	23	223	9.7	52	78, 9, 5, 4, 3, 1, .4
Yahoo.Autos	59	7202	6021	36	223	6.2	49	76, 13, 5, 2, 1, .9, .9, .4, .2, .2
Google.Movies	40	7285	6483	32	130	4.1	8	69, 15, 6, 3, 3, 1, 1, .7, .7, .7
Yahoo.Movies	45	8531	7433	38	130	3.4	7	64, 20, 8, 4, 2, 1, .6, .2
Google.Outdoors	38	7707	7260	30	135	4.5	6	76, 16, 6, 1
Yahoo.Outdoors	68	8756	8162	37	135	3.6	7	80, 11, 3, 2, 1, .7, .7, .5, .2, .2
Google.Photography	26	3661	3233	22	148	6.7	15	67, 18, 6, 4, 2, 2, 2, .5
Yahoo.Photography	35	3575	3014	26	148	5.7	11	59, 17, 9, 5, 3, 2, 2, .9, .4, .4
Google.Software	77	20471	18864	55	189	3.4	8	69, 15, 7, 4, 3, .9, .3, .3, .3, .3
Yahoo.Software	46	12222	10673	37	189	5.1	7	50, 14, 8, 6, 4, 3, 2, 1, .9, .9

Figure 11: Dataset Characteristics: Google & Yahoo! Slices (October 2000)

   
5.4 Experiments with Real Catalogs

Figure 12 shows the performance of the algorithm on the 10 datasets given in Figure 11. We tested the accuracy of the classifiers when merging the Yahoo! categorization into the corresponding Google categorization and vice versa. The enhanced algorithm did very well even though the two catalogs were quite different: 30% fewer errors on average (14.1% difference in absolute accuracy) when classifying Yahoo! into Google, and 26% fewer errors on average (14.3% difference in absolute accuracy) when classifying Google into Yahoo!.

  
(a) Yahoo! to Google (Train: Google, Test: Yahoo!)

	Accuracy		Improvement
Dataset	Basic	Enhanced	Absolute	Relative
Autos	60.5	76.2	15.7	40%
Movies	27.1	42.6	15.5	21%
Outdoors	65.2	77.8	12.6	36%
Photography	50.7	62.8	12.1	25%
Software	47.6	62.4	14.8	28%
Average	50.2	64.4	14.1	30%

(b) Google to Yahoo! (Train: Yahoo!, Test: Google)

	Accuracy		Improvement
Dataset	Basic	Enhanced	Absolute	Relative
Autos	50.2	73.1	22.9	46%
Movies	28.5	46.2	17.7	25%
Outdoors	55.9	65.4	9.5	22%
Photography	45.4	51.3	5.9	11%
Software	43.0	58.6	15.6	27%
Average	44.6	58.9	14.3	26%

Figure 12: Google & Yahoo!: Classification Accuracy

   
6. Conclusions

We presented a technique for integrating documents from a source catalog into a master catalog that takes advantage of the implicit information present in the source catalog: that documents in the same category in the source catalog are similar. Our technique enhances the standard Naive Bayes classification by incorporating this information when classifying source documents. We showed through analysis that the highest accuracy achievable with our enhanced technique can be no worse than what can be achieved with the standard Naive Bayes classification.

Our experiments using synthetic as well as real data indicate that the proposed technique can result in large accuracy improvements. Using a tune set for selecting the weight to give the implicit information allows our enhanced algorithm to do substantially better, and never do significantly worse. Our experiments also showed that the size of the tune set can be very small and hence not place a significant burden on the user of the system.

   
Appendix

A. Proofs

Consider the documents belonging to a category S in N. Let

$$f_i := \mbox{Number of documents from $S$\space predicted to be in $C_i$ }$$

For a document d, let

$$b_i := \vert C_i\vert \times \Pr(d \,\vert\,C_i)$$

From Eqs. 5 and 6, for a weight w

$$Pr(C_i \,\vert\,d, S) = K b_i f_i^w$$

where K is the same for all the documents in S (K is the product of the denominators in the two equations). We use the notation $Pr_w(C_i \,\vert\,d, S)$ to denote $Pr(C_i \,\vert\,d, S)$ for a weight w.

Theorem 1   For any positive pair of weights w₁, w₂, let w₁ > w₂, let C_x1 be the predicted category of document d at weight w₁, and C_x2 the predicted category at weight w₂. Then $f_{x_1} \geq f_{x_2}$.

Proof: Since C_x1 is the classification at weight w₁,
$\Pr_{w_1}(C_{x_1} \,\vert\,d, S) \geq \Pr_{w_1}(C_{x_2} \,\vert\,d, S)$. Expanding, we get

 

$$\geq$$ K b_x1 f_x1^w₁ K b_x2 f_x2^w₁

$$\geq$$ (b_x1/b_x2) (f_x1/f_x2)^w₁ 1 (6)

Similarly, since $\Pr_{w_2}(C_{x_1} \,\vert\,d, S) \leq \Pr_{w_2}(C_{x_2} \,\vert\,d, S)$, we get

 

$$\leq$$ K b_x1 f_x1^w₂ K b_x2 f_x2^w₂

$$\leq$$ (b_x1/b_x2) (f_x1/f_x2)^w₂ 1 (7)

Combining equations 7 and 8, we get

$$\begin{eqnarray*}(b_{x_1}/b_{x_2}) (f_{x_1}/f_{x_2})^{w_1} & \geq & (b_{x_1}/b_{... ...{~~~~~~~~~~(since $w_1-w_2 > 0$ )} \\ f_{x_1} & \geq & f_{x_2} \end{eqnarray*}$$

$\Box$

Lemma 2   For any category C_p, if there exists some C_j such that f_j > f_pand $b_j \geq b_p$, or f_j = f_p and b_j > b_p, then C_p will never be the classification of document d.

Proof: Let there be some C_j such that f_j > f_p and $b_j \geq b_p$. Then b_j f_j^w > b_p f_p^wfor any positive w, and $Pr_w(C_j \,\vert\,d, S) > Pr_w(C_p \,\vert\,d, S)$ for any positive w, and C_j will always be preferred to C_p. A similar argument holds for the other case. $\Box$

Lemma 3   Let C_p, C_q be two categories such that f_p > f_q and b_p < b_q. Then there exists some weight w_t > 0 such that for all w > w_t, $\Pr_w(C_p \vert d, S) > \Pr_w(C_q \,\vert\,d, S)$, and for all w < w_t, $\Pr_w(C_p \,\vert\,d, S) < \Pr_w(C_q \,\vert\,d, S)$.

Proof: Let $w_t = \log(b_q/b_p) / \log(f_p/f_q)$. Since f_p > f_q and b_q > b_p, w_t > 0. Now, for any w > w_t:

$$\begin{eqnarray*}w & > & \log(b_q/b_p) / \log(f_p/f_q) \\ w \log(f_p/f_q) & > &... ... (f_p/f_q)^w & > & (b_q/b_p) \\ K b_p f_p^w & > & K b_q f_q^w \end{eqnarray*}$$

Similarly for any w < w_t:

$$\begin{eqnarray*}w & < & \log(b_q/b_p) / \log(f_p/f_q) \\ K b_p f_p^w & < & K b_q f_q^w \end{eqnarray*}$$

$\Box$

Theorem 2   For each document d, there either exists a single interval (w₁, w₂), $0 \leq w_1 \leq w_2$ in which the document will be correctly classified, or the document will never be correctly classified.

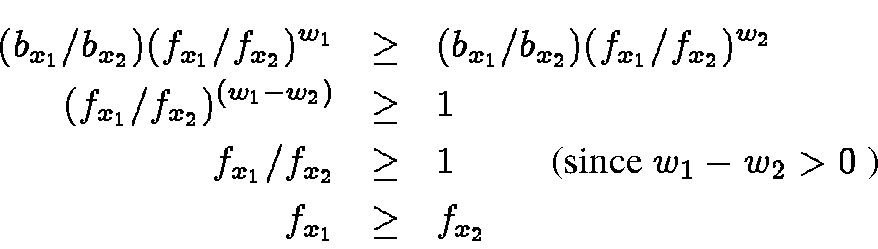
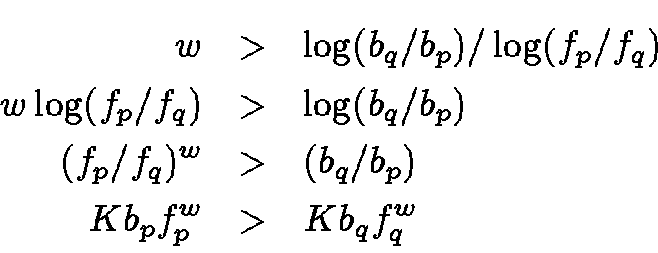
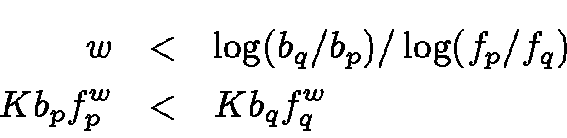
Proof: Let C_p be the correct classification for document d. We split all other categories into five groups:

• $G_{always} = \{ C_j \,\vert\,f_j > f_p \mbox{ and } b_j \geq b_p, \mbox{ or } f_j = f_p \mbox{ and } b_j > b_p \}$. From Lemma 2, if G_always is non-empty, the document will never be correctly classified.
• $G_{never} = \{ C_j \,\vert\,f_j < f_p \mbox{ and } b_j < b_p \}$. C_pwill always be preferred to any $C_j \in G_{never}$.
• $G_{equal} = \{ C_j \,\vert\,f_j = f_p \mbox{ and } b_j = b_p \}$. We assume that if two classes have the same probability, the document is assigned to both classes, and thus ignore this case.
• $G_{high} = \{ C_j \,\vert\,f_j > f_p \mbox{ and } b_j < b_p \}$. From Lemma 3, there exists some weight w_high such that for all w < w_high, $\Pr_w(C_p \,\vert\,d, S) > max(\{ \Pr_w(C_j \,\vert\, d, S) \,\vert\,C_j \in G_{high} \})$,
• $G_{low} = \{ C_j \,\vert\,f_j < f_p \mbox{ and } b_j > b_p \}$. From Lemma 3, there exists some weight w_low such that for all w > w_low, $\Pr_w(C_p \,\vert\,d, S) > max(\{ \Pr_w(C_j \,\vert\,d, S) \,\vert\,C _j \in G_{low} \})$.

Hence if G_always is non-empty, or if w_high < w_low, C_p will never the the classification for the document. Otherwise, the document will be correctly classified in the interval (w_low, w_high). $\Box$

Bibliography

ABS00

Rakesh Agrawal, Roberto Bayardo, and Ramakrishnan Srikant.
Athena: Mining-based Interactive Management of Text Databases.
In Proc. of the Seventh Int'l Conference on Extending Database Technology (EDBT), Konstanz, Germany, March 2000.

BFOS84

L. Breiman, J. H. Friedman, R. A. Olshen, and C. J. Stone.
Classification and Regression Trees.
Wadsworth, Belmont, 1984.

CDAR97

S. Chakrabarti, B. Dom, R. Agrawal, and P. Raghavan.
Using Taxonomy, Discriminants, and Signatures for Navigating in Text Databases.
In Proc. of the 23rd Int'l Conf. on Very Large Databases, pages 446-455, 1997.

Coh96

W.W. Cohen.
Learning Rules that Classify E-Mail.
In Proc. of the 1996 AAAI Spring Symposium on Machine Learning in Information Access, 1996.

DC00

S. T. Dumais and H. Chen.
Hierarchical classification of web content.
In Proc. of the 23rd Int'l ACM Conf. on Research and Development in Information Retrieval (SIGIR), pages 256-263, Athens, Greece, August 2000.

DPBA99

R. Dolin, J. Pierre, M. Butler, and R. Avedon.
Practical evaluation of IR within automated classification systems.
In Proc. of the 8th Int'l Conf. on Information and Knowledge Management (CIKM), Kansas City, Nov. 1999.

Goo65

I.J. Good.
The Estimation of Probabilities: An Essay on Modern Bayesian Methods.
M.I.T. Press, 1965.

Lan95

K. Lang.
News Weeder: Learning to Filter Net-News.
In Proc. of the 12th Int'l Conf. on Machine Learning, pages 331-339, 1995.

Lar99

Leah S. Larkey.
A patent search and classification system.
In The Fourth ACM Conference on Digital Libraries, pages 79-87, Berkeley, CA, August 99.

LR94

D.D. Lewis and M. Ringuette.
A comparison of two learning algorithms for text categorization.
In In Third Annual Symposium on Document Analysis and Information Retrieval, pages 81-92, 1994.

Mae94

P. Maes.
Agents that Reduce Work and Information Overload.
Communications of the ACM, 37(7):31-40, 1994.

Mit97

Tom M. Mitchell.
Machine Learning.
McGraw-Hill, 1997.

MN98

Andrew McCallum and Kamal Nigam.
A Comparison of Event Models for Naive Bayes Text Classification.
In AAAI-98 Workshop on ``Learning for Text Categorization'', 1998.

PB97

M. Pazzani and D. Billsus.
Learning and Revising User Profiles: The identification of interesting web sites.
Machine Learning, 27:313-331, 1997.

PE97

T.R. Payne and P. Edwards.
Interface Agents that Learn: An Investigation of Learning Issues in a Mail Agent Interface.
Applied Artificial Intelligence, 11:1-32, 1997.

SDHH98

M. Sahami, S. Dumais, D. Heckerman, and E. Horvitz.
A Bayesian Approach to Filtering Junk E-mail.
In Proc. of the AAAI'98 Workshop on Learning for Text Categorization, Madison, Wisconsin, 1998.

SK99

R. Segal and J. Kephart.
MailCat: An Intelligent Assistant for Organizing E-Mail.
In Proc. of the Third Int'l Conf. on Autonomous Agents, 1999.

SYB98

M. Sahami, S. Yusufali, and M.Q.W. Baldonado.
Sonia: A service for organizing networked information autonomously.
In Proc. of the Third ACM Conference on Digital Libraries, pages 200-209, 1998.

Footnotes

... categories¹

Catalogs are often organized as hierarchies. We assume that any documents assigned to an interior node really belong to a conceptual leaf node that is a child of that interior node. Since we now have documents only at leaf nodes, we can flatten the hierarchy to a single level and treat it as a set of categories. Note that a document can still belong to multiple leaf nodes, but documents are only in leaf nodes and not interior nodes.

... pairs.²

The essential idea is that if the document consists of both text and attributes, we can assume independence between the text and the attributes to compute $\Pr(d \,\vert\,C_i) = \Pr(d_{text} \,\vert\,C_i) \times \Pr(d_{attr} \,\vert\,C_i)$, where d_text is the text for the document description, and d_attr the set of attributes for the document.

... pages.³

From Google (http://directory.google.com), we got Recreation/Autos, Arts/Movies, Recreation/Outdoors, Arts/Photography and Computers/Software. From Yahoo! (http://dir.yahoo.com), we got the corresponding categories: Recreation/Automotive, Entertainment/Movies_and_Film, Recreation/Outdoors, Arts/Visual_Arts/Photography, and Computers_and_Internet/Software.