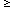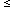An Adaptive Model for Optimizing Performance of an Incremental
Web Crawler
Jenny Edwards
1
,2,
Kevin McCurley3,
John Tomlin3
2
Faculty of Information Technology, University of Technology, Sydney,
PO Box 123, Broadway NSW 2007, Australia
3
IBM Research Division, Almaden Research Center,
650 Harry Road, San Jose CA 95120 6099, USA
[email protected], mccurley,[email protected]
Copyright is held by the author/owner.
WWW10,
May 1-5, 2001, Hong Kong.
ACM
1-58113-348-0/01/0005.
Abstract
This paper outlines the design of a web crawler implemented for IBM
Almaden's WebFountain project and describes an optimization model
for controlling the crawl strategy. This crawler is scalable and incremental.
The model makes no assumptions about the statistical behaviour of
web page changes, but rather uses an adaptive approach to maintain
data on actual change rates which are in turn used as inputs for the
optimization. Computational results with simulated but realistic data
show that there is
no "magic bullet" - different, but equally plausible, objectives lead to
conflicting "optimal" strategies. However, we find that there are compromise
objectives which lead to good strategies that are robust against a number
of criteria.
Keywords: Crawler, Incremental Crawler, Scalability, Optimization
1 Introduction
Web crawlers are an essential component of all search engines, and are
increasingly becoming important in data mining and other indexing
applications, but they must function somewhere between the cushion of Moore's
Law and the hard place of the exponential growth of the web. While some
have questioned whether such exponential growth is currently being
maintained [1], the trend towards automated production of
web pages from databases makes it likely that such growth will continue,
or even accelerate, in the immediate future. Given that the bandwidth
for conducting crawls is neither infinite nor free it is becoming
essential to crawl the web in a not only scalable, but efficient
way if some reasonable measure of quality or freshness is to be maintained.
The WebFountain crawler to be outlined in this paper is designed to
crawl the entire web repeatedly, keeping a local copy of up to 1 MB of the text
of each page, plus metadata, in a repository, which is to be used
for indexing, mining, etc. Furthermore this crawler is incremental,
that is, the repository copy of each page is updated as soon as
the actual web page is crawled. However, even using this technique, the
repository must always be out of date to some (we hope
minimal) extent. Our crawler, to be described in greater detail
below, has as an essential feature a set of queues of URLs to be
crawled, and several parameters which determine how URLs are to be selected
from these queues. The values of these parameters must be determined in
a way that leads to efficient crawling, and we present a
model which computes these parameters in such a way as to optimize some
objective related to freshness.
This model assumes that the web is crawled for some variable, but
pre-specified number of discretized time periods which together
constitute a cycle of the crawler.
Several definitions of freshness, which is non-trivial to measure, have been proposed by various authors, but
in this paper we take the view that a page in the repository is either
up-to-date, or obsolete, that is, it no longer matches the page
on the real web. Clearly it is desirable to minimize the number of such
pages, but we shall see that such an objective can be formulated in a
number of ways.
Pages become obsolete when they change on the real web between crawls,
but for simplicity we shall also consider the special case of new
pages, of which we have no copy in the repository, but
of which we become aware, either through new links, or exogenous
information, and define them as also being obsolete.
A particular feature of the model we describe is that it makes no
a priori assumptions about the way in which pages change, simply
that we can measure when changes occur, and record the frequency with
the pages' metadata. In this sense the model is adaptive in
that the more cycles the crawler is in operation, the more reliable
and refined is the data which we have available to drive it. For our
purposes a page change is required to be non-trivial, as
determined by a shingle (see Broder et al. [4]). Furthermore, while growth in the
web changes the data in our model, it has no effect on the size of the
model nor the solution time.
No previous work that we know of makes use of precisely this set of
assumptions, but much of it has some bearing on our model. After a
review of this work, we present a more detailed description of the
crawler, followed by a mathematical description of the optimization
model for the model parameters. We then describe a series of computational
experiments designed to test use of the model and some of its
variants on simulated but realistic data.
2 Previous Work
There have been several studies of web crawling in its relatively short
history, but most of them have had a focus rather different from ours. Some
have concentrated on aspects relating
to caching, eg Wills and Mikhailov[13] and Douglis et al. [9]. Others
have been principally interested in the most efficient and effective way
to update a fixed size database extracted from the web, often for some
specific function, such as data mining, see eg the work of Cho
et al. [5],[6],[7]. These studies were performed over time periods ranging
from a few days to seven months. However, for differing practical
reasons, these crawlers were restricted to subsets of web pages.
Several authors, eg Coffman et al. [8] approach crawling from a theoretical
point of view, comparing it to the polling systems of queueing theory, ie
multiple queue-single server systems.
However, the problem equivalent to the obsolescence time of a page
is unexplored in the queueing literature.
A common assumption has been that page changes
are a Poisson or memoryless process, with parameter
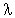 as the rate of change for the pages.
Brewington and Cybenko[1] and Cho and Garcia-Molina[6]
confirm this within the limits of their data gathering. This is somewhat
undermined by another study, based on an extensive subset of the web, by
Brewington and Cybenko[2] showing that most web pages are modified during
US working hours, ie 5am to 5pm (Silicon Valley Standard Time), Monday to
Friday. Nevertheless,
the widely accepted Poisson model forms the basis for a series of studies
on crawler strategies. These lead to a variety of analytical models designed
to minimize the age or maximize the freshness of a collection
by investigating:
as the rate of change for the pages.
Brewington and Cybenko[1] and Cho and Garcia-Molina[6]
confirm this within the limits of their data gathering. This is somewhat
undermined by another study, based on an extensive subset of the web, by
Brewington and Cybenko[2] showing that most web pages are modified during
US working hours, ie 5am to 5pm (Silicon Valley Standard Time), Monday to
Friday. Nevertheless,
the widely accepted Poisson model forms the basis for a series of studies
on crawler strategies. These lead to a variety of analytical models designed
to minimize the age or maximize the freshness of a collection
by investigating:
-
how often a page should be crawled
-
in what order pages should be crawled
-
whether a crawling strategy should be based on the importance of
pages or their rates of change
The definitions or metrics for freshness,
age and importance are not completely consistent, but
in general the freshness of a page refers to the difference
between the time of crawling a page and the current time,
while the age of a page is the difference between the time when the
page last changed and the current time.
Widely differing metrics have been offered for the
importance of a page, but as the total number of possible metrics
is large and the crawler in this study
does not currently use any of them, no formal definitions will
be given here.
While differing in detail, the experimental results in the referenced papers
agree on general trends, and in particular that:
-
the average size of individual pages is growing
-
the proportion of visual and other nontextual material is growing in comparison
to text
-
the number of pages has been growing exponentially
(Brewington and Cybenko[1] give two different estimates of 318
and 390 days for the web to double in size but also say that the growth
rate is slowing. However, see our comment at the beginning
of Section 1.)
- different domains have very different page change rates
-
the average age and lifetimes of pages are still quite low
(cf Tables 1 and 2).
While all of these trends are important for caching, the last three are more
relevant to the study of whole web crawling to be discussed here.
2.1 Crawling Models
In a series of papers, Cho et al.
([5],[6],[7]) address a number of issues relating to the design
of efficient crawlers. In [7] they examine different crawling strategies
using the Stanford University web pages as a particular subset of the web,
and examine several scenarios with different physical limitations
on the crawling. Their approach is to visit more important pages
first, and they describe a number of possible metrics for determining this,
as well as the order in which the chosen pages will be visited. They show
that it is possible to build crawlers which can obtain a significant portion
of important pages quickly using a range of metrics. Their model appears to
be most useful when trying to crawl large portions of the web with limited
resources, or when pages need to be revisited often to detect changes.
Cho and Garcia-Molina[6] derive a series of mathematical models
to determine the optimum strategy in a number of crawling scenarios, where
the repository's extracted copy of the web is of fixed size. They
examine models
where all pages are deemed to change at the same average or uniform
rate and where they change at different or non-uniform rates. For
a real life crawler, the latter is more likely to be relevant. For each
of these two cases, they examine a variety of synchronization or crawling
policies. How often the repository web copy is updated depends on the crawling
capacity or bandwidth available for the required number of pages. Within
that limitation is the question of how often each individual page should
be crawled to meet a particular objective such as maximizing freshness.
Cho and Garcia-Molina examine a uniform allocation policy, in which
each page is crawled at the same rate, and a non-uniform or proportional
policy where each page is crawled with a frequency that is proportional
to the frequency with which it is changed on the web, ie pages which are
updated frequently are crawled more often than those which change only
occasionally. Finally, they examine the order in which the pages should
be crawled. They develop models of:
-
fixed order where all pages are crawled repeatedly in the same order
each cycle
-
random order where all pages are crawled in each cycle but in
a random order, eg by always starting with the root URL for a site and
crawling all pages linked to it
-
purely random where pages are crawled on demand, which may mean
some pages are crawled frequently and others never.
Their models show that when pages change at a uniform rate, maximum freshness
or minimum age is obtained by crawling pages at a uniform rate and in fixed
order. As we have noted, most studies make the assumption that pages change
at a variable
rate which may be approximated by a Poisson distribution, but in the second
stage of their study, Cho and Garcia-Molina assume the broader gamma
distribution
for this change rate. Moreover, they prove that their particular model is
valid for any distribution, and conclude that when pages change
at varying rates, it is always better to crawl these pages at a uniform
rate, ie ignoring the rate of change, than at a rate which is proportional
to the rate of change. However, to maximize freshness they find a closed
form solution to their model which provides an optimal crawling rate which
is better than the uniform rate. These results were all derived for a
batch or periodic
crawler, where a fixed number of pages is crawled in a
given time period. These pages are used to update
a fixed size repository either by replacing existing repository pages with
newer versions or by replacing less important pages with those
deemed to be of greater importance.
Coffman et al. [8] built a theoretical model to minimize the fraction
of time pages spend out of date. Also assuming Poisson
page change processes, and a general distribution for page access time,
they similarly show that optimal results can be obtained by crawling pages as
uniformly as possible.
In [5], Cho and Garcia-Molina devise an architecture for an
incremental crawler, and examine the use of an incremental
versus a batch crawler under various conditions, particularly
those where the entire web is not crawled. Crawling a subset (720,000 pages
from 270 sites) of the web daily, they determined statistics on the rate
of change of pages from different domains. They found, for example, that
for the sites in their survey, 40% of pages in the .com domain change daily
in contrast to .edu and .gov domains where more than 50% of pages did not
change in the four months of the study. They show that the rates of change
of pages they crawled can be approximated by a Poisson distribution, with
the proviso that the figures for pages which change more
often than daily or less often than four monthly are inaccurate. Using
different collection procedures, Wills and Mikhailov[13] derive similar
conclusions.
A disadvantage of all these models is that they deal only with a
fixed size repository of a limited subset of the web. In contrast, our model is
flexible, adaptive, based upon the whole web and caters gracefully for its growth.
2.2 Page Statistics Derived from Crawling
Statistics on page ages, lifetimes, rates of change, etc are
important for our model. Subject to the assumptions of
a constant size repository copy of the web, which is updated with
periodic uniform reindexing, Brewington and Cybenko[1] showed
that in order to be sure that a randomly chosen page is at least 95% fresh
or current up to a day ago, the web (of 800M) pages needs a reindexing
period of 8.5 days, and a reindexing period of 18 days is needed to be 95%
sure that the repository copy of a random page was current up to 1 week ago.
In another study[2], the same authors
estimate the cumulative probability function
for the page age in days on a log scale as shown in Table 1.
|
| cumulative probability |
page age (days) |
|
| 0.03 |
100 |
| 0.14 |
101 |
| 0.48 |
102 |
| 0.98 |
103 |
Table 1: Cumulative Probability Distribution of Page Age in Days
As with similar studies, this does not accurately account for pages which
change very frequently, or those which change very slowly. Allowing for
these biases, the authors also estimate the cumulative probability
of mean lifetime in days, shown in Table 2:
|
| cumulative probability |
mean lifetime (days) |
|
| 0.0 |
100 |
| 0.12 |
101 |
| 0.40 |
102 |
| 1.00 |
.6*103 |
Table 2: Cumulative Probability Distribution of Mean Lifetime in Days
Brewington and Cybenko then use their data
to examine various reindexing strategies based on a single revisit period
for all pages, and refer to the need for mathematical optimization to
determine the optimal reindexing strategy, when the reindexing period varies
per page. Such a model is precisely the main focus of this paper.
3 The WebFountain Crawler
The model in this paper is designed to address the efficiency of a
crawler recently built at IBM as part of the WebFountain
data mining architecture. The features of this crawler that
distinguish it from most previous crawlers are that it is fully
distributed and incremental. By distributed, we mean
that the responsibility for scheduling, fetching, parsing and storing
is distributed among a homogeneous cluster of machines. URLs are
grouped by site, and a site is assigned to a machine in the cluster
(a few very large sites such as geocities may actually be split among
several machines). There is no global scheduler, nor are there any
global queues to be maintained. Moreover, there is no machine
with access to a global list of URLs.
An incremental crawler (as opposed to a batch
crawler) is one that runs as an ongoing process, and the crawl is
never regarded as complete.
The underlying philosophy is that the local collection of documents
will always grow, always be dynamic, and should be constructed with
the goal of keeping the repository as fresh and complete as
possible. Instead of devoting all of its effort to crawling newly
discovered pages, a percentage of its time is devoted to recrawling
pages that were crawled in the past, in order to minimize the number of
obsolete pages. Note that our use of the term "incremental" differs
from that of Cho et al. [5],[6],[7]. Their definition assumes that the
document collection is of static size, and a ranking function is
used to replace documents in the collection with more important
documents. We regard the issue of incrementality to be independent of
the size of the collection, and we allow for growth of the crawler,
in order to meet the demands of an ever-expanding web.
The WebFountain crawler is written in C++, is fully distributed, and
uses MPI (Message Passing Interface) for communication between the
different components. The three major components are the Ants,
which are the
machines assigned to crawl sites, duplicate detectors, which are
responsible for detecting duplicates or near-duplicates, and a single
machine called a Controller. The Controller is the control point for
the machine cluster, and keeps a dynamic list of site assignments on the Ants.
It is also responsible for routing messages for discovered URLs, and
manages the overall crawl rate, monitoring of disk space, load
balancing, etc.
Other crawlers have been written that distribute the load of crawling
across a cluster, but they generally distribute the work in different
ways. Due to the competitive nature of the Internet indexing and
searching business, few details are available about the latest
generation of crawlers.
The first generation Google crawler [3] is apparently designed as a batch crawler,
and is only partially distributed. It uses a single point of control for
scheduling of URLs to be crawled. While this might appear convenient,
it also provides a bottleneck for intelligent scheduling algorithms,
since the scheduling of URLs to be crawled may potentially need to
touch a large amount of data (eg, robots.txt, politeness values, change rate data,
DNS records, etc). Mercator[10] supports incremental crawling using priority values on
URLs and interleaving crawling new and old URLs.
The crawl scheduling mechanism of the WebFountain crawler resembles Mercator
in that it is fully distributed, very flexible, and can even be changed on the fly.
This enables efficient use of all crawling processors and their underlying network.
The base software component for determining the ordering on URLs to be crawled
consists of a composition of sequencers. Sequencers are
software objects that implement a few simple methods to determine
the current backlog, whether there are any URLs available to be crawled,
and control of loading and flushing data structures to disk.
Sequencers are then implemented according to different policies,
including a simple FIFO queue or a priority queue. Other Sequencers
are combiners, and implement a policy for joining sequencers.
Examples include a round robin aggregator, or a priority aggregator that
probabilistically selects from among several sequencers according to
some weights. In addition, we use the Sequencer mechanism to
implement the crawling politeness policy for a site. The ability
to combine sequencers and cascade them provides a very convenient
means to build a flexible recrawl strategy.
The strategy that we decided on for implementing the crawl strategy is
illustrated in Figure 1.
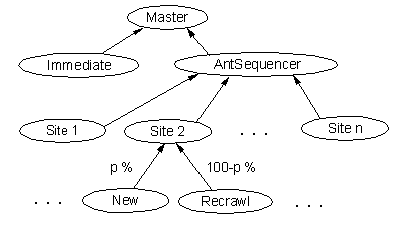
Figure 1: The Structure of Queues that Feed the URL Stream in
the WebFountain Crawler
At the top level, there are two queues, one
for immediate crawling that is intended to be used from a GUI, and one
that aggregates all other URLs. Under that, each Ant is assigned a
list of sites to be crawled, and maintains an active list of
approximately 1000 sites that are currently being crawled. The
selection of URLs to be crawled is taken from this active list in a
round robin fashion.
This avoids crawling any particular site too frequently -
the so called politeness criterion. In addition, each Ant
is multithreaded to minimize latency effects.
When a site is added to the active list, a
sequencer is constructed that loads all data structures from disk,
merges the list of newly discovered URLs with the list of previously
crawled URLs for that site, and prepares two queues. One of these
queues contains URLs that have never been crawled, and one contains
URLs that are scheduled for a recrawl.
It is the way in which we manage our never-crawled and recrawl lists that
is to be determined by our optimization model. politeness
4 Model Description
We constructed this model for robustness under both growth of the web and
changes to its underlying nature. Hence we do not make any a priori assumptions
about the distribution of page change rates. However, we do make an
assumption that particular historical information on each page is maintained in
the metadata for that page. Specifically, each time a page is crawled,
we record whether that page has changed since it was last crawled, and use
this information to put the page into one of (at most 256) change-frequency
"buckets", recorded as one byte of the page's metadata. Clearly, such data
becomes more reliable as the page ages.
In practice, page change rates may range from as
often as every 15 minutes to as infrequently
as once a year or less (eg a government department contact page). The very
rapidly changing pages (several times a day) are almost all media sites
(CNN, for example) and we feel that this relatively small and specialized set
of sites should be handled separately.
The remaining pages in the repository are grouped into B buckets
each containing bi pages
which have similar rates of change.
a priori B buckets
bi
A (theoretically)complete crawl of the web is modeled as taking place in a
crawler cycle.
Both the number of time periods in such a cycle, T,
and the (equal) length of each period may be varied as needed.
Our fundamental requirement is to estimate the number of obsolete pages in
each frequency bucket at the end of each time period. The way in which
this is calculated is best illustrated by following the tree of
alternatives in Figure 2.
We consider a generic time period and a generic bucket (dropping the
subscript) of pages in the
repository, containing
b pages at the beginning of the time period. Let the number of
such pages for which our repository copy is already obsolete at the
beginning of the time period be y, leaving (b-y) up-to-date.
Now let x be the
number of pages in this bucket crawled during the time period,
and assume that obsolete and up-to-date pages are crawled with equal
probability. This gives the partition of pages in the bucket seen at the
second level of branches in the tree. Finally, let a be the (given)
proportion of pages which change in the bucket during the time period,
and assume that such a change is detected if the page is crawled in the same
time period. The b pages in the bucket are now partitioned among
the leaves of the tree, and we easily see that the leaves
marked * correspond to obsolete pages.
Note that by adding the expressions attached to these two leaves
we obtain an expression for the number of obsolete pages at the end
of this time period, as a function of the data at the beginning of
the period and of the decision variable x, which specifies how many
pages in this bucket to crawl. This relationship is fundamental to our model,
and to the way in which the queue of "old" URLs is managed.

Figure 2: Identification of Obsolete Pages in each Bucket
per Time Period
In addition to the "old" pages we must deal with the "new" pages either
discovered or exogenously supplied during the crawl.
Let the number of these new pages crawled
during a time period be z (these are then added
to the appropriate buckets in the repository). The remaining new uncrawled
pages are represented by n. These pages are also regarded as obsolete
and will remain in that state until crawled.
We are now ready to give
the definitions of the variables and the formal model.
|
|
| T |
= |
number of time periods in model |
| B |
= |
number of buckets, where bucket refers to pages which
change at approximately the same rate |
| cconstit |
= |
average time in seconds to crawl an old page in bucket
i in time period t |
| dconstt |
= |
average time in seconds to crawl a new page in time
period t |
| Cconstt |
= |
total number of seconds available for crawling in
time period t |
| oldwtit |
= |
experimental proportional weight on crawling obsolete
pages in bucket i in time period
t |
| newwtt |
= |
experimental proportional weight on crawling new
pages in time period t |
| oldnwtit |
= |
probability that when an old page in bucket i
is crawled in time period t, it finds a
new page
|
| newnwtt |
= |
probability that when a new uncrawled page is crawled
in time period t,
it finds a new page |
| nconst |
= |
minimum number of new pages brought to the attention of the
crawler per time period |
| bit |
= |
number of pages in bucket i
at the end of time period t |
| pi |
= |
distribution of new pages to buckets
where pi is proportional
to bi and
|
|
|
|
B

i =1
|
pi = 1
|
|
| ait |
= |
fraction of pages in bucket i
which change in time period t |
| yit |
= |
number of obsolete pages in bucket i
at end of time period t |
| xit |
= |
number of crawled pages in bucket i
in time period t |
| nt |
= |
number of new uncrawled pages at end of time period t
|
| zt |
= |
number of new pages crawled in time period t. |
|
The objective of the time period model is to minimize the weighted sum of
obsolete pages, ie:
|
|
|
|
|
|
|
|
|
|
T

t =1
|
|
B

i =1
|
oldwtityit + newwttnt
|
|
|
|
|
| subject to the following constraints:
|
|
|
|
|
| The bandwidth available for
crawling during each time period may not be exceeded.
|
|
|
|
|
|
B

i =1
|
cconstitxit
+dconsttzt
|
|
(1) |
| The number of obsolete existing
or old pages, yit
is updated as discussed above at every time period.
|
|
|
|
|
| (1-(xit/
bi,t-1))((1-ait)
yi,t-1
+ aitbi,t-1) |
|
(2) |
|
The number of new uncrawled pages,
nt is updated every time period. |
|
|
|
|
| nt-1 + |
B

i =1
|
oldnwtit
xit
+ (newnwtt-1)zt +nconst
|
|
(3) |
| The total number of pages in each
bucket, bit is updated in every time period. |
|
|
|
|
|
(4) |
The number of existing pages, xit
crawled in any bucket in any time period
must be fewer
than the total number of pages
available to be crawled in the bucket,
bi,t-1. |
|
|
|
|
|
(5) |
Similarly, in any
time period,
the number of new pages
crawled, zt must be
less than
the number of new uncrawled pages,
nt-1. |
|
|
|
|
|
(6) |
|
|
|
|
| Each constraint holds for all t = 1,
....,T
and, where relevant, for all i = 1,
....,B. |
|
|
|
The critical solution outputs are the ratios xit/
bit and the zt values, which tell
us how many URLs in the "old" and "new" queues we should crawl in each
time period, and hence the probabilities p in Figure 1.
5 Solution
Since the balance equation
2 for updating yit is highly nonlinear,
the model must be solved by a nonlinear programming (NLP) method capable of
solving large scale problems. For our model runs, it was assumed
that there are 500M unique pages on the web, with
a growth rate which allows the web to double in size in approximately 400
days. With a value of 14 for the number of time periods T, and
255 for B, the number of buckets, the basic model has approximately
11200 variables, of which 10000 are nonlinear and 11200 constraints, of which
about 3300 are nonlinear. Even after the use of various presolve techniques
to reduce the size of the problem, solution proved to be non-trivial.
We used the NEOS[12] public server system to run
experiments
with several different NLP solvers on the models and found that the standard
NLP package MINOS[11] gave the best and most reliable
results. Solution times for all variations of the model were around ten
minutes on a timeshared machine.
Since the WebFountain crawler for which this model was designed is in its
early stages of development, we have very little actual historical data for
such parameters as the rate of change of various pages. We have therefore
used simulated, but realistic data, based on the previous studies we have
cited from the literature.
5.1 Results
Since our model runs use estimated data, many experiments were run for
a range of values of the critical parameters. Reassuringly, the model is
quite robust under most of these changes. However, it turns out to be quite
sensitive to changes in the weights
in the objective function, oldwtit and newwtt.
Given the overall aim of minimising the total number of obsolete pages,
we describe the implementation of three of the many possible variations of the
objective function weights:
oldwtit newwtt
-
Strategy 1 gives equal weights (summing to 1) to each time period in a
cycle of the crawler
-
Strategy 2 gives the last time period the total weight of 1 and the other
time periods, zero weight, ie the model is minimising the number of obsolete
pages just on the last time period of a crawler cycle
-
Strategy 3 gives the last time period a high weighting and the remaining
time periods very low weightings, ie it is still trying to minimise the
number of obsolete pages in the last time period but it is also taking
into account the obsolete pages in all time periods.
|
| |
objective |
Total Pages at end |
Total Obsolete Pages at end |
|
| Strategy 1 |
32.592×107 |
5.224×108 |
3.086×107 |
| Strategy 2 |
1.722×107 |
5.184×108 |
1.609×107 |
| Strategy 3 |
2.138×107 |
5.224×108 |
1.702×107 |
Table 3: Model Statistics
5.2 Experiment 1
As shown in Table 3, Strategy 2 gives the minimum value of
the objective
function, ie the weighted total of obsolete pages at the end of a crawler cycle,
followed by Strategy
3. The objective value for Strategy 1 is considerably higher. Figure 3 illustrates
the effects
of implementing these strategies.
Strategy 2 recommends crawling each page
just once during a cycle of the crawler. This uniform crawling is
in line with the theoretical results of Cho and Garcia-Molina [6] and
Coffman et al. [8]. Strategy 1 recommends crawling fast changing pages
in many time periods of a cycle. For these pages, the crawl rate is
usually higher even than the page change rate. However, it does not crawl
at all, those pages which fall into the lowest 40% of page change rates.
Strategy 3 is a compromise. It recommends crawling all pages at least once in
a crawler cycle with the fastest
changing 18% being crawled more than once per cycle.

Figure 3: Recommended Number
of Crawls per Crawler Cycle for Pages with Different Change Rates under Different Crawl Strategies
Table 3 also shows that while the total
number of web pages in the repository at the end of a crawler cycle
is similar under
each strategy, the total number of obsolete pages is not. Figure 4
examines the total number of obsolete pages in each time period of a
cycle under each
strategy.

Figure 4: Total Number of Obsolete Pages each Time Period
under Different Stategies
If we disregard the actual objective function and look at the number of
obsolete pages we see that in any given time period (except the last),
Strategy 1 always has fewer obsolete pages than Strategy 3 and considerably
fewer than Strategy 2. Because of the weights in the objective functions
for the different strategies, the lower number of obsolete pages for
Strategies 2 and 3 in the last time period is expected.
Mathematically, Strategy 2 is optimal. However, depending on the purpose(s)
for which a crawler is designed, it may not be acceptable to have an
incremental
crawler ignore the page change rate and crawl all pages at a uniform rate,
ie just once each crawler cycle. In terms of minimizing the
number of obsolete pages each time period, Strategy 1 is clearly superior.
However, it does not crawl 40% of the pages during a cycle. This may
also be unacceptable for many of the possible uses of the crawler.
Strategy 3 again provides a reasonable compromise. It crawls all pages
within a cycle and still has a somewhat lower mathematical minimum objective
value than Strategy 1.
5.3 Experiment 2
Many versions of the model were run changing
the values of different parameters. In all cases the results were as expected.
Experiment 2 is a typical example. In the initial or Version 1 of the model,
the 500M repository pages were assumed to be distributed equally to each bucket,
ie it was assumed that there are the same number of pages corresponding
to each of the different page change rates. Each of the 255 buckets received
2M pages. In Version 2, the buckets representing the 25% of the fastest
changing page rates and the 25% of the slowest changing pages all received
3M pages initially. The buckets representing the middle 50% of page change
rates, each received 1M pages initially. Table 4
shows the effect on the total number of obsolete pages of this change.
|
| |
objective |
Total Pages at end |
Total Obsolete Pages at end |
|
| Strategy 1 v1 |
32.592×107 |
5.224×108 |
3.086×107 |
| Strategy 1 v2 |
37.744×107 |
5.214×108 |
3.534×107 |
| Strategy 3 v1 |
2.138×107 |
5.224×108 |
1.702×107 |
| Strategy 3 v2 |
2.500×107 |
5.193×108 |
1.972×107 |
Table 4: Model Statistics for Versions 1 and 2 of Strategies 1 and 3
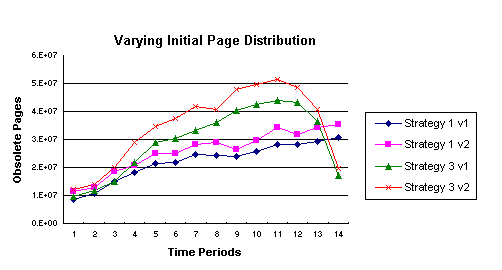
Figure 5: Effects on the Number of Obsolete Pages per Time Period
of Varying
the Page Change Rates Distribution
Figure 5 shows that this change made little difference to the distribution
of obsolete pages for each time period. For both Strategy 1 and Strategy
3, there are a larger number of obsolete pages in Version 2. This is expected
as the models in Version 2 started with a higher number of obsolete pages
and given the finite capacity of the crawler, this number will grow
during a 14 time period cycle of the crawler unless forced to reduce as in
the last few time periods of Strategy 3.
Experiment 2 does show the robustness of the model to changes in the
initial parameters.
5.4 Experiment 3
The object of Experiment 3 was to determine if the number
of obsolete pages continued to grow with time, or if this number reached
stabilisation. There were four runs, all of the model with an objective
corresponding to Strategy1. Figure 6 illustrates the results.
Strategy 1 (Version 1) was run
for 14 time periods and for 28 time periods as was Version 3.
In Version
3, it was assumed that the page change rates were half as frequent as in
Version 1. The distribution of obsolete pages over time periods between
and within each version shows the expected similarities. As can be seen
in any given time period, the number of obsolete pages for Version 3 is
approximately half that of Version 1. More importantly, it can be seen
that for both versions, the number of obsolete pages is tending to stabilise.
It was not possible to run the crawler model for a longer period and obtain
a useful mathematical solution, nor would the crawler be run for this long
in practice without an update of the parameters and reoptimisation.
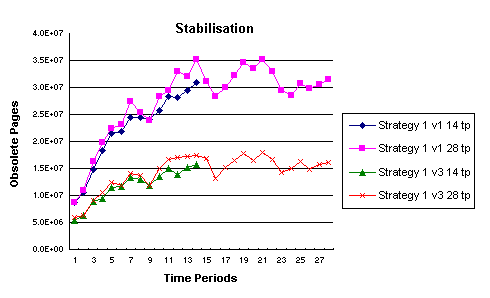
Figure 6: Trend towards Stabilisation in the
Number of Obsolete Pages over Time
The objectives we used, based on the different weighted sums of obsolete pages,
correspond to maximising the freshness of the collection under different crawler
aims, eg all the web must be crawled each cycle or a certain percentage of
pages in the repository should be guaranteed to be no more than say, a week old.
Taking all the experiments into consideration, the
results are consistent with an implementation philosophy of
using Strategy 2 in early cycles of the crawler, to drive down the
number of obsolete pages in the repository quickly. It would then
be beneficial to switch to Strategy 1 or 3 to maintain a stable
number.
6 Conclusions
The computational results we have obtained (albeit with simulated data)
suggest that an efficient crawling strategy can be implemented for the
WebFountain (or any) incremental crawler without making any theoretical
assumptions
about the rate of change of pages, but by using information gleaned
from actual cycles of the crawler which adaptively build up more
extensive and reliable data. Thus the model we have described is adaptive
at two levels: within a crawler cycle it coordinates the management of the
URL queues over the cycle's component time periods, and between cycles
the data necessary for the optimization is updated for the next cycle -
particularly the change rates,
and new page creation rates. We look forward to full scale implementation
of the model when the WebFountain crawler begins regular operation.
7 Acknowledgements
The authors would like to thank members of IBM's WebFountain team, in
particular, Sridhar Rajagopalan and Andrew Tomkins. They would also like
to thank Michael Saunders of Stanford University and the NEOS team
for help with the solution of the nonlinear programming problems and
Paula Wirth for technical assistance.
References
- Brewington, B. & Cybenko, G. (2000a) How Dynamic is the Web?,
Proceedings of the 9th World Wide Web Conference (WWW9)
- Brewington, B. & Cybenko, G. (2000b) Keeping Up with the Changing
Web, Computer, May, pp 52-58
- Brin, S. & Page, L. (1998) The Anatomy of a Large-Scale
Hypertextual Web Search Engine, Proceedings of the 7th World Wide Web Conference,
(WWW7), http://www-db.stanford.edu/~backrub/google.html
- Broder, A.Z., Glassman, S.C., Manasse, M.S. & Zweig, G. (1997)
Syntactic Clustering of the Web, Proceedings of 6th International World
Wide Web Conference (WWW6). http://www.scope.gmd.de/info/www6/technical/paper205/paper205.html
- Cho, J. & Garcia-Molina, H (2000b) The Evolution of the Web and
Implications for an Incremental Crawler, Proceedings of 26th International
Conference on Very Large Databases (VLDB)
- Cho, J. & Garcia-Molina, H. (2000a) Synchronizing a Database to
Improve Freshness, Proceedings of 2000 ACM International Conference
on Management of Data (SIGMOD)
- Cho, J. Garcia-Molina, H. & Page, L (1998) Efficient Crawling
Through URL Ordering, Proceedings of the 7th World Wide Web Conference
(WWW7)
- Coffman, E., Liu, Z. & Weber, R. (1997) Optimal Robot Scheduling
for Web Search Engines, Rapport de recherche no 3317, INRIA Sophia
Antipolis
- Douglis, F., Feldmann, A. & Krishnamurthy, B. (1997) Rate of Change
and other Metrics: a Live Study of the World Wide Web, Proceedings
of USENIX Symposium on Internetworking Technologies and Systems
- Heydon, A. & Najork, M. (1999) Mercator: A Scalable, Extensible Web
Crawler , World Wide Web, 2(4), 219-229
- MINOS
(http://www.sbsi-sol-optimize.com/Minos.htm)
- NEOS Server for Optimization
(http://www-neos.mcs.anl.gov)
- Wills, C. & Mikhailov, M. (1999) Towards a Better Understanding
of Web Resources and Server Responses for Improved Caching, Proceedings
of the 8th World Wide Web Conference (WWW8)
Vitae
 |
Jenny Edwards received her PhD in Computer Science from the University
of Sydney. Her research interests include mathematical programming and
algorithms for parallel processing. She has been an academic in the
Faculty Of Information Technology at the University of Technology,
Sydney since 1976. She is a member of ACS, INFORMS and the Mathematical
Programming Society.
She is currently on a year's leave, some of which is being spent at
IBM Almaden Research Center where this work was completed.
|
 |
Kevin S. McCurley joined IBM Almaden Research Center in
1987. He received a Ph.D. in Mathematics from the University of Illinois,
and has previously held positions at Michigan State University, University
of Southern California, and Sandia National Laboratories. His current research
interests include information security and web technologies. |
 |
John Tomlin gained his B.Sc.(Hons) and Ph.D. in mathematics
at the University of Adelaide, South Australia. His current interests are
in large scale optimization, sparse matrices and the World Wide Web. He
joined the IBM Research Division in 1987. He is a member of ACM, INFORMS
and the Mathematical Programming Society. |
Footnotes:
1
This work
was completed while the author was on leave at IBM Almaden Research Center
�
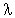 as the rate of change for the pages.
Brewington and Cybenko[1] and Cho and Garcia-Molina[6]
confirm this within the limits of their data gathering. This is somewhat
undermined by another study, based on an extensive subset of the web, by
Brewington and Cybenko[2] showing that most web pages are modified during
US working hours, ie 5am to 5pm (Silicon Valley Standard Time), Monday to
Friday. Nevertheless,
the widely accepted Poisson model forms the basis for a series of studies
on crawler strategies. These lead to a variety of analytical models designed
to minimize the age or maximize the freshness of a collection
by investigating:
as the rate of change for the pages.
Brewington and Cybenko[1] and Cho and Garcia-Molina[6]
confirm this within the limits of their data gathering. This is somewhat
undermined by another study, based on an extensive subset of the web, by
Brewington and Cybenko[2] showing that most web pages are modified during
US working hours, ie 5am to 5pm (Silicon Valley Standard Time), Monday to
Friday. Nevertheless,
the widely accepted Poisson model forms the basis for a series of studies
on crawler strategies. These lead to a variety of analytical models designed
to minimize the age or maximize the freshness of a collection
by investigating: