Various access methods have been developed to support efficient search and retrieval over text document collections. Examples include suffix arrays [12], inverted files or inverted indexes [22,29], and signature files [5]. Inverted files have traditionally been the index structure of choice on the Web. Commercial search engines use custom network architectures and high-performance hardware to achieve sub-second query response times using such inverted indexes.
An inverted index over a collection of Web pages consists of a set of inverted lists, one for each occurring word (or index term). The inverted list for a term is a sorted list of locations where the term appears in the collection. A location consists of a page identifier and the position of the term within the page. When it is not necessary to track each term occurrence within a page, a location will include just a page identifier (and optionally the number of occurrences within the page). Given an index term w, and a corresponding location l, we refer to the pair (w,l) as a posting for w.
Conceptually, building an inverted index involves processing each page to extract postings, sorting the postings first on index terms and then on locations, and finally writing out the sorted postings as a collection of inverted lists on disk. When the collection is small and indexing is a rare activity, optimizing index-building is not as critical as optimizing run-time query processing and retrieval. However, with a Web-scale index, index build time also becomes a critical factor for two reasons:
Scale and growth rate. The Web is so large and growing so rapidly [11,28] that traditional build schemes become unmanageable, requiring huge resources and taking days to complete (and becoming more vulnerable to system failures). As a measure of comparison, the 40 million page (220 GB) WebBase repository [9] represents only about 4% of the estimated size of the publicly indexable Web as of January 2000 [28], but is already larger than the 100GB very large TREC-7 collection [8], the benchmark for large IR systems.
Rate of change. Since the content on the Web changes extremely rapidly [4], there is a need to periodically crawl the Web and update the inverted index. Indexes can either be updated incrementally or periodically rebuilt, after every crawl. With both approaches, the key challenge is to handle the large whole-scale changes commonly observed between successive crawls of the Web. For efficiency and simplicity, most commercial Web search systems employ the rebuilding approach [15]. In this case, it is critical to build the index rapidly to quickly provide access to the new data.
To study and evaluate index building in the context of the special challenges imposed by the Web, we have implemented a testbed system that operates on a cluster of nodes (workstations). As we built the testbed, we encountered several challenging problems that are typically not encountered when working with smaller collections. In this paper we report on some of these issues and the experiments we conducted to optimize build times for massive collections. In particular:
We emphasize that the focus of this paper is on the actual process of building an inverted index and not on using this index to process search queries. As a result, we do not address issues such as ranking functions, relevance feedback [22,29], and distributed query processing [10,24].
We also wish to clarify that the focus of this paper is not on presenting a comprehensive performance or feature-list comparison of our testbed indexing system with existing systems for indexing Web and non-Web collections. Rather, we use our experience with the testbed to identify some key performance issues in building a Web-scale index and propose generic techniques that are applicable to any distributed inverted index system.
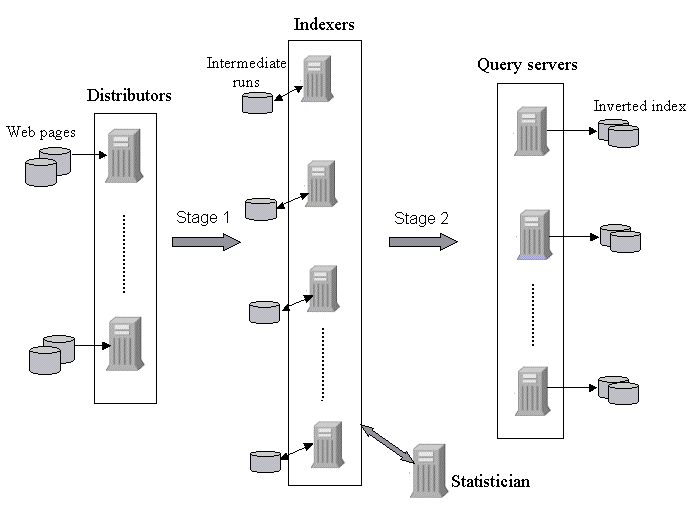
Our testbed system for building inverted indexes operates on a distributed shared-nothing architecture consisting of a collection of nodes connected by a local area network. We identify three types of nodes in the system (Figure 1):
Distributors.These nodes store the collection of Web pages to be indexed. Pages are gathered by a Web crawler and stored in a repository distributed across the disks of these nodes [9].
Indexers.These nodes execute the core of the index building engine.
Query servers. Each of these nodes stores a portion of the final inverted index and an associated lexicon. The lexicon lists all the terms in the corresponding portion of the index and their associated statistics. Depending on the organization of the index files, some or all of the query servers may be involved in answering a search query.
Note that many traditional information retrieval (IR) systems do not employ such a 3-tier architecture for building inverted indexes. In those systems, the pages or documents to be indexed are placed on disks directly attached to the machines that build the index. However, a 3-tier architecture provides significant benefits in the context of a Web search service. Note that a Web search service must perform three resource intensive tasks --- crawling, indexing, and querying --- simultaneously. Even as existing indexes are used to answer search queries, newer indexes (based on a more recent crawl) must be constructed, and in parallel, the crawler must begin a fresh crawl. A 3-tier architecture clearly separates these three activities by executing them on separate banks of machines, thus improving performance. This ensures that pages are indexed and made available for querying as quickly as possible, thereby maximizing index freshness.
Overview of indexing process. The inverted index is built in two stages. In the first stage, each distributor node runs a distributor process that disseminates the collection of Web pages to the indexers. Each indexer receives a mutually disjoint subset of pages and their associated identifiers. The indexers parse and extract postings from the pages, sort the postings in memory, and flush them to intermediate structures on disk.
In the second stage, these intermediate structures are merged together to create one or more inverted files and their associated lexicons. An (inverted file, lexicon) pair is generated by merging a subset of the sorted runs. Each (inverted file, lexicon) pair is transferred to one or more query servers depending on the degree of replication. In this paper, for simplicity, we assume that each indexer builds only one such pair.
Distributed inverted index organization. In a distributed environment, there are two basic strategies for distributing the inverted index over a collection of query servers [13,20,23]. One strategy is to partition the document collection so that each query server is responsible for a disjoint subset of documents in the collection (called local inverted files in [20]). The other option is to partition based on the index terms so that each query server stores inverted lists only for a subset of the index terms in the collection (called global inverted files in [20]). Performance studies described in [23] indicate that the local inverted file organization uses system resources effectively and provides good query throughput in most cases. Hence, our testbed employs the local inverted file organization.
Testbed environment. Our indexing testbed uses a large repository of Web pages provided by the WebBase project [9] as the test corpus for the performance experiments. The storage manager of the WebBase system receives pages from the Web crawler [4] and populates the distributor nodes. The indexers and the query servers are single processor PC's with 350--500 MHz processors, 300--500 MB of main memory, and equipped with multiple IDE disks. The distributor nodes are dual-processor machines with SCSI disks housing the repository. All the machines are interconnected by a 100 Mbps Ethernet LAN.
The core of the indexing system is the index-builder process that executes on each indexer. The input to the index-builder process is a sequence of Web pages and their associated identifiers.1 The output of the index-builder is a set of sorted runs. Each sorted run contains postings extracted from a subset of the pages received by the index-builder.
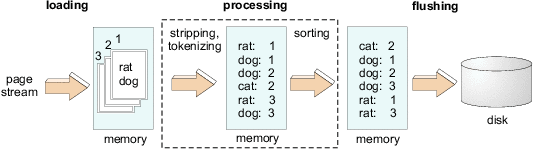
The process of generating these sorted runs can logically be split into three phases, as illustrated in Figure 2. We refer to these phases as loading, processing, and flushing. During the loading phase, some number of pages are read from the input stream. The processing phase involves two steps. First, the pages are parsed to remove HTML tagging, tokenized into individual terms, and stored as a set of postings in a memory buffer. In the second step, the postings are sorted in-place, first by term, and then by location. During the flushing phase, the sorted postings in the memory buffer are saved on disk as a sorted run. These three phases are executed repeatedly until the entire input stream of pages has been consumed.
Loading, processing and flushing tend to use disjoint sets of system resources. Processing is obviously CPU-intensive, whereas flushing primarily exerts secondary storage, and loading can be done directly from the network, tape, or a separate disk. Therefore, indexing performance can be improved by executing these three phases concurrently. Since the execution order of loading, processing and flushing is fixed, these three phases together form a software pipeline.
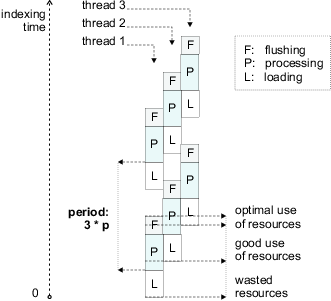
Figure 3 illustrates the benefits of pipelined parallelism during index construction. The figure shows a portion of an indexing process that uses three concurrent threads, operates on three reusable memory buffers, and generates six sorted runs on disk.
The key issue in pipelining is to design an execution schedule for the different indexing phases that will result in minimal overall running time (also called makespan in the scheduling literature). Our problem differs from a typical job scheduling problem [3] in that we can vary the sizes of the incoming jobs, i.e., in every loading phase we can choose the number of pages to load. In the rest of this section, we describe how we make effective use of this flexibility. First, we derive, under certain simplifying assumptions, the characteristics of an optimal indexing pipeline schedule and determine the theoretical speedup achievable through pipelining. Next, we describe experiments that illustrate how observed performance gains differ from the theoretical predictions.
Let us consider an indexer node that has one resource of each type: a single CPU, a single disk, and a single network connection over which to receive the pages. How should we design the pipeline shown in Figure 2 to minimize index construction time?
First, notice that executing concurrent phases of the same kind, such as two disk flushes, is futile, since we have only one resource of each type. Consider an index-builder that uses N executions of the pipeline to process the entire collection of pages and generate N sorted runs. By an execution of the pipeline, we refer to the sequence of three phases --- loading, processing, and flushing --- that transform some set of pages into a sorted run. Let Bi, i = 1..N, be the buffer sizes used during these N executions. The sum B1+...+BN = Btotal is fixed for a given amount of text input and represents the total size of all the postings extracted from the pages. Our aim is to come up with a way of choosing the Bi values so as to minimize the overall running time.
Now, loading and flushing take time linear in the size of the buffer. Processing
time has a linear component (representing time for removing HTML and tokenizing)
and a linear-logarithmic component (representing sorting time). Let
li =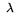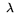 
Bi, fi = 
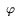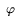Bi,
and pi = 
Bi + 
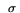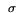Bi
log(Bi) represent the durations of the loading, flushing, and
processing phases for the ith execution of the pipeline.2 For large N, the overall indexing time is
determined by the scarcest resource (the CPU, in Figure 3) and can be
approximated by Tp = max{l1+..+lN,
p1+..+pN, f1+..+fN}.
It can be shown (see [14]) that Tp is minimized when all N
pipeline executions use the same buffer size B, where B =
B1..= BN = Btotal/N. Let l = 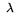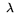B, f =
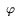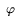B, and p = B + 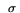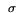B log(B) be the durations of the loading,
processing, and flushing phases, respectively. We must choose a value of B
that maximizes the speedup gained through pipelining.
We calculate speedup as follows. Pipelined execution takes time Tp =
N max{l,p,f} (6p in Figure 3) and uses 3 buffers, each of size B. In
comparison, sequential execution using a single buffer of size 3B will
take time Ts = N/3 (l' + p' + f'), where l' = 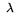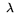(3B), f' =
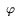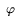(3B), and p' = (3B) + 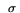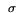(3B) log(3B). Thus, in a node with
a single resource of each type, the maximal theoretical speedup that we can
achieve through pipelining is (after simplification):
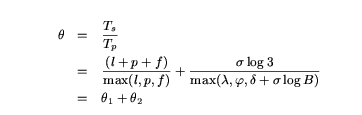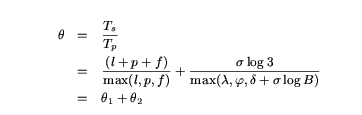
Now,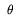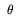 
1 >= 1 whereas 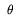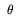2 <= (
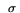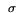log(3))/max{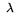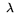,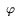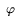} << 1 for typical values of , ,
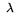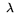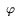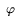and 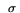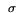(refer to Table 1). Therefore, we ignore 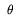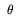2 and
concentrate on choosing the value of B that maximizes
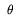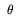1. The maximum value of 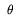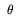1 is 3, which is
reached when l = p = f, i.e., when all three phases are of equal duration. We
cannot guarantee l = f since that requires 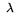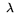= 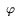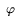. However, we can
maximize 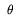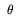1 by choosing p = max{l,f} so that 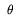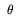1
= 2 + min{l,f}/max{l,f}.
For example, in Figure 3, the ratio between the phases is l:p:f = 3:4:2. Thus,
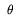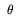1 for this setting is (3+4+2)/4 = 2.25. We could improve
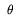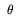1 by changing the ratio to 3:3:2, so that 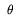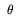1 =
2 + 2/3 ~ 2.67. In general, setting B + 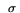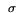B log(B) = max{ 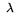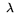B,
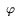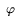B}, we obtain
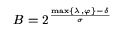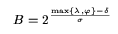
This expression represents the size of the postings buffer that must be used to
maximize the pipeline speedup, on an indexer with a single resource of each
type. If we use a buffer of size less than the one specified by the above
equation, loading or flushing (depending on the relative magnitudes of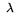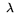
and 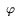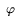) will be the bottleneck and the processing phase will be forced to
periodically wait for the other phases to complete. An analogous effect will
take place for buffer sizes greater than the one prescribed by the above
equation. In [14] we generalize this equation to handle indexers with multiple
CPUs and disks.
To study the impact of the pipelining technique on indexing performance, we conducted a number of experiments on our testbed, using a single indexer supplied with a stream of Web pages from a distributor.
|
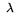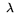1.26 * 10-3 |
|
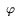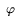4.62 * 10-4 |
|
6.74 * 10-4 |
|
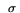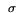2.44 * 10-5 |
We first ran the index-builder process in measurement mode, where we
recorded the execution times of the various phases and determined the values of
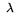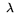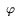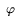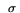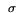, , , and (Table 1). Using the values of these
constants in equation (1), we evaluate B to be 16 MB. Therefore, the
optimal total size of the postings buffers, as predicted by our theoretical
analysis, is 3B = 48 MB.
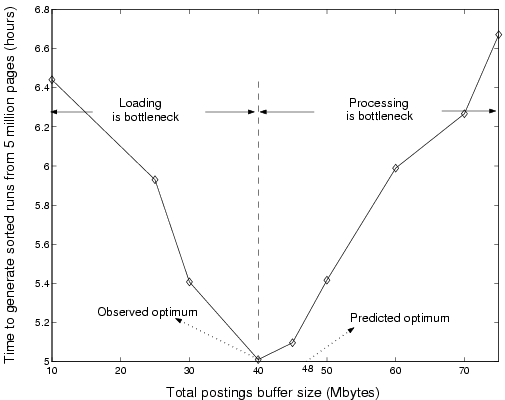
Impact of buffer size on performance. Figure 4 illustrates how the performance of the index-builder process varies with the size of the buffer. It highlights the importance of the analytical result as an aid in choosing the right buffer size. The optimal total buffer size based on actual experiments turned out be 40 MB. Even though the predicted optimum size differs slightly from the observed optimum, the difference in running times between the two sizes is less than 15 minutes for a 5 million page collection. For buffer sizes less than 40, loading proved to be the bottleneck, and both the processing and flushing phases had to wait periodically for the loading phase to complete. However, as the buffer size increased beyond 40, the processing phase dominated the execution time as larger and larger buffers of postings had to be sorted.
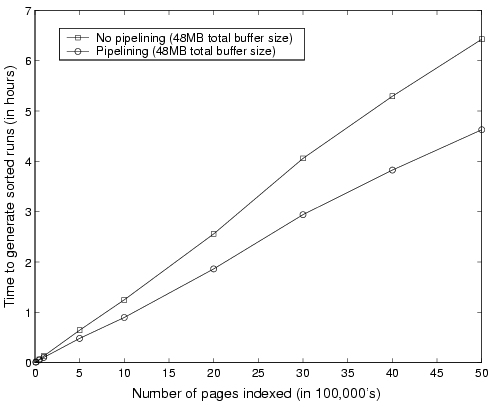
Performance gain through pipelining. Figure 5 shows how pipelining impacts the time taken to process and generate sorted runs for a variety of input sizes. Note that for small collections of pages, the performance gain through pipelining, though noticeable, is not substantial. This is because small collections require very few pipeline executions and the overall time is dominated by the time required at startup (to load up the buffers) and shutdown (to flush the buffers). This is one of the reasons that pipelined index building has not received prior attention as most systems dealt with smaller collections. However, as collection sizes increase, the gain becomes more significant and for a collection of 5 million pages, pipelining completes almost 1.5 hours earlier than a purely sequential implementation. Our experiments showed that, in general, for large collections, a sequential index-builder is about 30--40% slower than a pipelined index-builder. Note that the observed speedup is lower than the speedup predicted by the theoretical analysis described in the previous section. That analysis was based on an ``ideal pipeline,'' in which loading, processing and flushing do not interfere with each other in any way. In practice, however, network and disk operations do use processor cycles and access main memory. Hence, any two concurrently running phases, even of different types, do slow down each other.
Note that for a given total buffer size, pipelined execution will generate sorted runs that are approximately 3 times smaller than those generated by a sequential indexer. Consequently, 3 times as many sorted runs will need to be merged in the second stage of indexing. However, other experiments described in [14] show that even for very large collection sizes, the potential increase in merging time is more than offset by the time gained in the first stage through pipelining. We expect that as long as there is enough main memory at merge time to allocate buffers for the sorted runs, performance will not be substantially affected.
When building inverted indexes over massive Web-scale collections, the choice of an efficient storage format is particularly important. There have traditionally been two approaches to storing and managing inverted files; either using a custom implementation or by leveraging existing relational or object data management systems [2,7].
The advantage of a custom implementation is that it enables very effective optimizations tuned to the specific operations on inverted files (e.g., caching frequently used inverted lists, compressing rarely used inverted lists using expensive methods that may take longer to decompress). Leveraging existing data management systems does not allow such fine-grained control over the implementation but reduces development time and complexity. However, the challenge lies in designing a scheme for storing inverted files that makes optimal use of the storage structures provided by the data management system. The storage scheme must be space efficient and must ensure that the basic lookup operation on an inverted file (i.e., retrieving some or all of the inverted list for a given index term) can be efficiently implemented using the native access methods of the data management system.
In this section we present and compare different storage schemes for managing large inverted files in an embedded database system. To test our schemes, we used a freely available embedded database system called Berkeley DB [19], that has been widely deployed in many commercial applications.
An embedded database is a library or toolkit that provides database support for applications through a well-defined programming API. Unlike traditional database systems that are designed to be accessed by applications, embedded databases are linked (at compile-time or run-time) into an application and act as its persistent storage manager. They provide device-sensitive file allocation, database access methods (such as B-trees and hash indexes), and optimized caching, with optional support for transactions, locking, and recovery. They also have the advantage of much smaller footprints compared to full-fledged client-server database systems.
In the following, we briefly the sketch the capabilities of Berkeley DB and propose a B-tree based inverted file storage scheme called the mixed-list scheme. We qualitatively and quantitatively compare the mixed-list scheme with two other schemes for storing inverted lists in Berkeley DB databases.
Berkeley DB provides a programming library for managing (key,value) pairs, both of which can be arbitrary binary data of any length. It offers four access methods, including B-trees and linear hashing. Berkeley DB supports transactions, locking, and recovery, all of which can be turned off, if desired, for efficiency. We chose to use the B-tree access method since it efficiently supports prefix searches (e.g., retrieve inverted lists for all terms beginning with ``pre'') and has higher reference locality than hash-based indexes.
The standard organization of a B-tree based inverted file involves storing the index terms in the B-tree along with pointers to inverted lists that are stored separately. Such an organization, though easy to implement using Berkeley DB, does not fully utilize the capabilities of the database system. Since Berkeley DB efficiently handles arbitrary sized keys and values, it is more efficient to store both the index terms and their inverted lists within the database. This enables us to leverage Berkeley DB's sophisticated caching schemes while retrieving large inverted lists with a minimum number of disk operations.
Storage schemes. The challenge is to design an efficient scheme for organizing the inverted lists within the B-tree structure. We considered three schemes (a qualitative comparison of these storage schemes is summarized in Table 2):
Figure 6 illustrates the mixed-list storage scheme. For simplicity, in
this example, we assume that no additional
information is maintained along with each posting. However, in our actual
implementation, we allocated a 2-byte payload field, to store extra
posting-level information.
The top half of the figure depicts inverted lists for four successive
index terms and the bottom half shows
how they are stored as (key,value) pairs using the mixed-list
scheme. For example, the second (key,value) pair in the figure, stores
the set of postings (cat,311), (cat,328),
(catch,103), (catcher,147), etc., with the first posting
stored in the key and the remaining postings stored in the value. As indicated
in the figure, the postings in the value are compressed by using prefix
compression for the index terms and by representing successive location
identifiers in terms of their numerical difference. For example, the posting
(cat,328) is represented by the sequence of entries 3 <an
empty field> 17, where 3 indicates the length of the common
prefix between the words for postings (cat,311) and (cat,328),
the
| Scheme | Index size | Zig zag joins | Hot updates |
| single payload | -- | + | + |
| full list | +- | - | - |
| mixed list | +- | +- | +- |
Index size. The crucial factors determining index size are the number of internal pages (a function of the height of the B-tree) and the number of overflow pages (which Berkeley DB uses to handle large value fields). In the single payload scheme, every posting corresponds to a new key, resulting in rapid growth in the number of internal pages of the database. For large collections, the database size becomes prohibitive even though Berkeley DB employs prefix compression on keys. Also, at query time, many performance-impeding disk accesses are needed. The situation is significantly better with the full list scheme. A database key is created only for every distinct term, and the value field can be well compressed. However, many terms occur only a few times in the collection whereas others may occur in almost every page. To accommodate such large variations in the size of the value field, many overflow pages are created in the database. In comparison, with the mixed list scheme, the length of the value field is approximately constant. This limits the number of overflow pages. Moreover, the total number of keys (and hence the number of internal pages) can be further reduced by choosing a larger size for the value field. However, since the value field can contain postings of different index terms, it is not compressed as well as with full lists.
Zig-zag joins. The ability to selectively retrieve portions of an inverted list can be very useful when processing conjunctive search queries on an inverted file. For example, consider the query green AND catchflies. The term green occurs on the Web in millions of documents, whereas catchflies produces only a couple of dozen hits. A zig-zag join [6] between the inverted lists for green and catchflies allows us to answer the query without reading out the complete inverted list for green. The single payload scheme provides the best support for zig-zag joins as each posting can be retrieved individually. In the full list scheme, the entire list must be retrieved to compute the join, whereas with the mixed list scheme, access to specific portions of the inverted list is available. For example, in Figure 6, to retrieve locations for cat starting at 311, we do not have to read the portion of the list for locations 100--280.
The skipped-list and random inverted-list structures of [17] and [18] also provide selective access to portions of an inverted list, by dividing the inverted list into blocks each containing a fixed number of postings. However, those schemes assume a custom inverted file implementation and are not built on top of an existing data management system.
Hot updates. Hot updates refers to the ability to modify the index at query time. This is useful when very small changes need to be made to the index between two successive index rebuilds. For example, Web search services often allow users and organizations to register their home pages with their service. Such additions can be immediately accommodated in the index using the hot update facility, without having to defer them till the index is next rebuilt.
In all three schemes, the concurrency control mechanisms of the database can be used to support such hot updates while maintaining consistency. However, the crucial performance factor is the length of the inverted list that must be read, modified, and written back to achieve the update. Since we limit the length of the value field, hot updates are faster with mixed lists than with full lists. The single payload scheme provides the best update performance as individual postings can be accessed and modified.
Notice that all three schemes significantly benefit from the fact that the postings are first sorted and then inserted. Inserting keys into the B-tree in a random order negatively affects the page-fill factor, and expensive tree reorganization is needed. Berkeley DB is optimized for sorted insertions so that high performance and a near-one page-fill factor can be achieved in the initial index construction phase.
Table 2 shows that the mixed-list scheme provides the best balance between small index size and support for efficient zig-zag joins. In the following section, we present a quantitative comparison of storage and retrieval efficiency for the three storage schemes discussed in this section.
The experimental data presented in this section were obtained by building an inverted index over a collection of 2 million Web pages. The collection contains 4.9 million distinct terms with a total of 312 million postings. 4
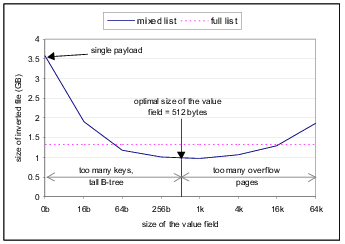
Figure 7 illustrates how the choice of the storage scheme affects the size of the inverted file. It shows the variation of index size with value field size when using the mixed-list scheme. The dotted line represents the index size when the same database was stored using the full-list scheme. Note that since the value field size is not applicable to the full-list scheme, the graph is just a horizontal line. The single payload scheme can be viewed as an extreme case of the mixed scheme with value field being empty. Figure 7 shows that both very small and very large value fields have an adverse impact on index size. In the mixed list scheme, very small value fields will require a large number of internal database pages (and a potentially taller B-tree index) to accommodate all the postings. On the other hand, very large value fields will cause Berkeley DB to allocate a large number of overflow pages which in turn lead to a larger index. As indicated in the figure, a value field size of 512 bytes provided the best balance between these two effects. The full-list scheme results in a moderate number of both overflow pages and internal database pages. However, it still requires around 30% more storage space than the optimal mixed-list inverted file. For all of the examined storage schemes, the time to write the inverted file to disk was roughly proportional to the size of the file.
| Number of pages (million) |
Input size (GB) |
Index size (GB) |
Index size (%age) |
| 0.1 | 0.81 | 0.04 | 6.17 |
| 0.5 | 4.03 | 0.24 | 6.19 |
| 2.0 | 16.11 | 0.99 | 6.54 |
| 5.0 | 40.28 | 2.43 | 6.33 |
Table 3 shows how the index size (using the mixed-list scheme) varies with the size of the input collection. The index sizes listed in Table 3 include the sum of the sizes of the inverted files and the associated lexicons. The numbers for Table 3 were generated by using mixed-lists with the optimal value field size of 512 bytes derived from Figure 7. Table 3 shows that the mixed-list storage scheme scales very well to large collections. The size of the index is consistently below 7% the size of the input HTML text. This compares favorably with the sizes reported for the VLC2 track (which also used crawled Web pages) at TREC-7 [8] where the best reported index size was approximately 7.7% the size of the input HTML. Our index sizes are also comparable to other recently reported sizes for non-Web document collections using compressed inverted files [18]. Note that exact index sizes are dependent on the type and amount of information maintained along with each posting (e.g., information to handle proximity queries). However, we believe that the 2-byte payload field used in our implementation can accommodate most posting-level information normally stored in inverted indexes.
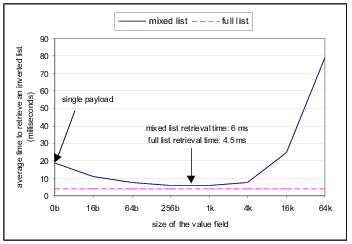
Figure 8 illustrates the effect of value field size on inverted list retrieval time. Once again, the dotted horizontal line represents the retrieval time when using the fixed-list scheme. Figure 8 was produced by generating uniformly distributed query terms and measuring the time required to retrieve the entire inverted list for each query term. A warming-up period was allowed, before the measurements, to fill the database and file system cache. The optimal retrieval performance in the mixed-list scheme is achieved when the value field size is between 512 and 1024 bytes. Notice that (from Figures 7 and 8) a value field size of 512 bytes results in maximum storage as well as maximum retrieval efficiency for the mixed-list scheme. Figure 8 also indicates that both the fixed-list and mixed-list (with optimal value field size) schemes provide comparable retrieval performance.
Note that Figure 8 only measures the raw inverted list retrieval performance of the different storage schemes. True query processing performance will be affected by other factors such as caching (of inverted lists), use of query processing techniques such as zig-zag joins, and the distribution of the query terms.
Most text-based retrieval systems use some kind of collection-wide information to increase effectiveness of retrieval [26]. One popular example is the inverse document frequency (IDF) statistics used in ranking functions. The IDF of a term is the inverse of the number of documents in the collection that contain that term. If query servers have only IDF values over their local collections, then rankings would be skewed in favor of pages from query servers that return few results. In order to offer effective rankings to the user, query servers must know global IDF values.
Depending on the particular global statistic, the ranking function, and the nature of the collection, it may or may not be necessary for a statistic to be computed accurately. In some cases, it might suffice to estimate the global statistic from the local values at the individual query servers. However, in this section, we analyze the problem of gathering accurate collection-wide information (with minimum overhead), for the cases where this is required. We present two techniques that are capable of gathering different types of collection-wide information, though here we focus on the problem of collecting term-level global statistics, such as IDF values. Term-level refers to the fact that any gathered statistic describes only single terms, and not higher level entities such as pages or documents.
Some authors suggest computing global statistics at query time. This would require an extra round of communication among the query servers to exchange local statistics. This communication adversely impacts query processing performance, especially for large collections spread over many servers. Since query response times are critical, we advocate precomputing and storing statistics at the query servers during index creation.
Our approach is based on using a dedicated server, known as the statistician, for computing statistics. Having a dedicated statistician allows most computation to be done in parallel with other indexing activities. It also minimizes the number of conversations among servers, since indexers exchange statistical data with only one statistician. Local information is sent to the statistician at various stages of index creation, and the statistician returns global statistics to the indexers in the merging phase. Indexers then store the global statistics in the local lexicons. A lexicon consists of entries of the form (term, term-id, local-statistics, global-statistics), where the terms stored in a lexicon are only those terms occurring in the associated inverted file (Section 2).
In order to avoid extra disk I/O, local information is sent to the statistician only when it is already in memory. We have identified two phases in which this occurs: flushing --- when sorted runs are written to disk, and merging --- when sorted runs are merged to form inverted lists and the lexicon. Sending information in these two phases leads to two different strategies with various tradeoffs which are discussed in the next section. We note here only that by sending information to the statistician in these phases without additional I/O's, a huge fraction of the statistic collection is eliminated.
Sending information to the statistician is further optimized by summarizing the postings. In both identified phases, postings occur in at least partially sorted order, meaning multiple postings for a term pass through memory in groups. Groups are condensed into (term, local aggregated information) pairs which are sent to the statistician. For example, if an indexer holds 10,000 pages that contain the term ``cat'', instead of sending 10,000 individual postings to the statistician, the indexer can count the postings as they pass through memory in a group and send the summary (``cat'', 10000) to the statistician. The statistician receives local counts from all indexers, and aggregates these values to produce the global document frequency for ``cat''. This technique greatly reduces network overhead in collecting statistics.
| Phase | Statistician load | Memory usage | Parallelism | |
| ME | merging | +- | + | +- |
| FL | flushing | - | - | ++ |
Here we describe and compare the two strategies mentioned above for sending information to the statistician. Table 4 summarizes their characteristics. The column titled ``Parallelism,'' refers to the degree of parallelism possible within each strategy.
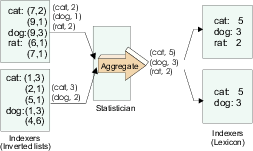
ME Strategy (sending local information during merging). Summaries for each term are aggregated as inverted lists are created in memory, and sent to the statistician. The statistician receives parallel sorted streams of (term, local-aggregate-information) values from each indexer and merges these streams by term, aggregating the sub-aggregates for each term to produce global statistics. The statistics are then sent back to the indexers in sorted term order. This approach is entirely stream based, and does not require in-memory or on-disk data structures at the statistician or indexer to store intermediate results. However, using streams means that the progress of each indexer is synchronized with that of the statistician, which in turn causes indexers to be synchronized with each other. As a result, the slowest indexer in the group becomes the bottleneck, holding back the progress of faster indexers. Figure 9 illustrates the ME strategy for collecting document frequency statistics for each term. Note that the bottom lexicon does not include statistics for ``rat'' because the term is not present in the local collection.
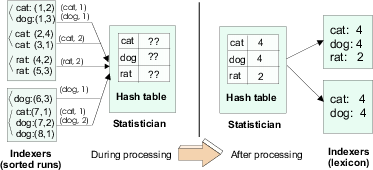
FL Strategy (sending local information during flushing). As sorted runs are flushed to disk, postings are summarized and the summaries sent to the statistician. Since sorted runs are accessed sequentially during processing, the statistician receives streams of summaries in globally unsorted order. To compute statistics from the unsorted streams, the statistician keeps an in-memory hash table of all terms and their related statistics, and updates the statistics as summaries for a term are received. At the end of the processing phase, the statistician sorts the statistics in memory and sends them back to the indexers. Figure 10 illustrates the FL strategy for collecting document frequency statistics.
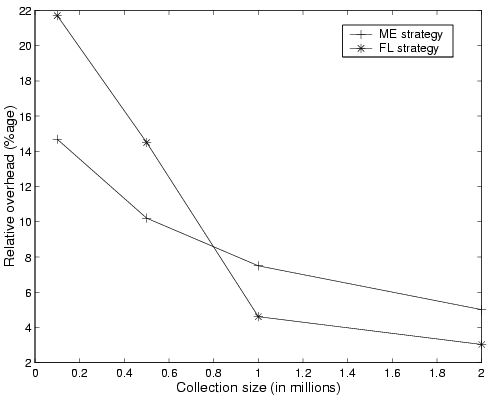
To demonstrate the performance and scalability of the collection strategies, we ran the index-builder and merging processes on our testbed, using a hardware configuration consisting of four indexers. We experimented with four different collection sizes - 100000, 500000, 1000000, and 2000000 pages, respectively. The results are shown in Figure 11, where we can see the relative overhead (defined as (T2-T1)/T1 where T2 is the time for full index creation with statistics collection and T1 is the time for full index creation with no statistics collection) for both strategies. In general, experiments show the FL strategy outperforming ME, although they seem to converge as the collection size becomes large. Furthermore, as the collection size grows, the relative overheads of both strategies decrease.
Comparison of strategies. At first glance ME might be expected to outperform FL: since the statistician receives many summary streams in FL, but only one from each indexer in ME, it performs more comparison and aggregation in FL than in ME. However, as mentioned earlier, merging progress in ME is synchronized among the servers. Hence, a good portion of computation done at the statistician cannot be done in parallel with merging activities at the indexer.
In FL, on the other hand, the indexer simply writes summaries to the network and continues with its other work. The statistician can then asynchronously process the information from the network buffer in parallel. However, not all work can be done in parallel, since the statistician consumes summaries at a slower rate than the indexer writes them to network, and the network buffer generally cannot hold all the summaries from a sorted run. Hence there is still nontrivial waiting at the indexer during flushing as summaries are sent to the statistician.
Enhancing parallelism. In the ME strategy, synchronization occurs when an indexer creates a lexicon entry and summary for a term, sends the summary to the statistician, and then waits for the global statistic to be returned so that the lexicon entry can be completed. To reduce the effect of synchronization, the merging process can instead write lexicon entries to a lexicon buffer, and a separate process will wait for global statistics and include them in the entries. In this way, the first process need not block while waiting, and both processes can operate in parallel.
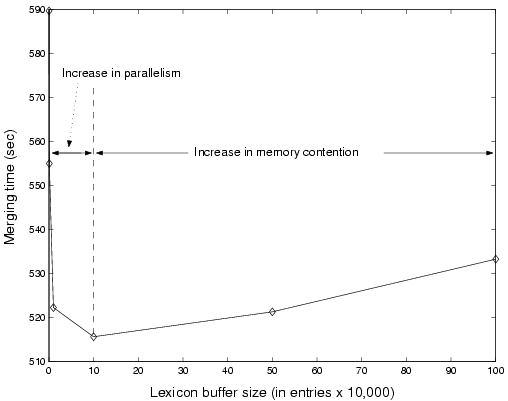
Figure 12 shows the effect of lexicon buffer size on merging performance over a collection of a million pages. Because lexicon entries are created faster than global statistics are returned on all indexers but the slowest, the lexicon buffer often becomes full. When this occurs, the process creating lexicon entries must block until the current state changes. Because larger lexicon buffers reduce the possibility of saturation, we expect and see that initial increases in size result in large performance gains. As lexicon buffer size becomes very large, however, performance slowly deteriorates due to memory contention. Although the entire buffer need not be present in memory at any one time, the lexicon buffer is accessed cyclically; therefore LRU replacement and the fast rate at which lexicon entries are created cause buffer pages to cycle rapidly through memory, swapping out other non-buffer pages.
Sub-linear growth of overhead. The constant decrease of the ME and FL relative overhead in Figure 11 can be explained by the fact that the number of distinct terms in a page collection is a sub-linear function of collection size. The overhead incurred by gathering statistics grows linearly with the number of terms in the collection, while the cost of index creation grows linear-logarithmically with the size of the collection. As a result, overhead of statistic collection will display sub-linear growth with respect to index creation time. This prediction is consistent with our experimental results.
However, the decreasing relative overhead for FL is subject to the constraint that the hashtable can fit in memory. Considering that a collection of a billion pages would require a hash table of roughly 5--6 GB in size 5, this constraint may become a problem for very large collections. While a memory of 6 GB is not completely unreasonable, a simple alternative using only commodity hardware would be to run several statisticians in parallel, and partition the terms alphabetically between statisticians. In this way, each statistician can collect and sort a moderately sized set of global statistics. We have not yet implemented this option in our system.
Motivated by the Web, there has been recent interest in designing scalable techniques to speed up inverted index construction using distributed architectures. In [21], Ribeiro-Neto, et al. describe three techniques to efficiently build an inverted index using a distributed architecture. However, they focus on building global (partitioning index by term), rather than local (partitioning by collection), inverted files. Furthermore, they do not address issues such as global statistics collection and optimization of the indexing process on each individual node.
Our technique for structuring the core index engine as a pipeline has much in common with pipelined query execution strategies employed in relational database systems [6]. Chakrabarti, et al. [3] present a variety of algorithms for resource scheduling with applications to scheduling pipeline stages.
There has been prior work on using relational or object-oriented data stores to manage and process inverted files [2,7]. Brown, et al. [2] describe the architecture and performance of an information retrieval system that uses a persistent object store to manage inverted files. Their results show that using an "off-the-shelf" data management facility improves the performance of an information retrieval system, primarily due to intelligent caching and device-sensitive file allocation. We experienced similar performance improvements for the same reasons by employing an embedded database system. Our storage format differs greatly from theirs because we utilize a B-tree storage system and not an object store.
References [26] and [27] discuss the questions of when and how to maintain global statistics in a distributed text index, but their techniques only deal with challenges that arise from incremental updates. We wished to explore strategies for gathering statistics during index construction.
A great deal of work has been done on several other issues, relevant to inverted-index based information retrieval, that have not been discussed in this paper. Such issues include index compression [16,18,29], incremental updates [1,10,25,29,30], and distributed query performance [23,24].
In this paper we addressed the problem of efficiently constructing inverted indexes over large collections of Web pages. We proposed a new pipelining technique to speed up index construction and showed how to choose the right buffer sizes to maximize performance. We demonstrated that for large collection sizes, the pipelining technique can speed up index construction by several hours. We proposed and compared different schemes for storing and managing inverted files using an embedded database system. We showed that an intelligent scheme for packing inverted lists in the storage structures of the database can provide performance and storage efficiency comparable to tailored inverted file implementations. Finally, we identified the key characteristics of methods for efficiently collecting global statistics from distributed inverted indexes. We proposed two such methods and compared and analyzed the tradeoffs thereof.
In the future, we intend to extend our testbed to incorporate distributed query processing and explore algorithms and caching strategies for efficiently executing queries. We also intend to experiment with indexing and querying over larger collections and integration of our text-indexing system with indexes on the link structure of the Web.
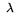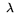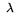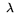= 1 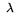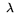2, where
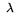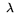1 is the rate at which pages can be loaded into memory from
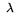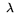the network and 2 is the average ratio between the size of a
page and the total size of the postings generated from that page
Sergey Melnik is currently a research scholar in the Computer Science department at Stanford University, California. His research interests include interoperability of Web databases and digital libraries, distributed systems, and knowledge representation. He received a Masters (M.S.) in Computer Science from Leipzig University, Germany in 1999 where he currently participates in a graduate research program.
Sriram Raghavan is currently a Ph.D student in the Computer Science department at Stanford University, Stanford, California. He received a Bachelor of Technology (B.Tech) degree in Computer Science and Engg. from the Indian Institute of Technology, Chennai, India in 1998 and a Masters (M.S) in Computer Science from Stanford University in 2000. His research interests include information management on the Web, large-scale searching and indexing, database and IR systems integration, and Web query processing.
Beverly Yang is currently a Ph.D. student in the Computer Science department at Stanford University, California. She received a Masters (M.S.) in Computer Science at Stanford University in 2000. Her research interests include information management on the Web and peer-to-peer systems.
Hector Garcia-Molina is the Leonard Bosack and Sandra Lerner Professor in the Departments of Computer Science and Electrical Engineering at Stanford University, Stanford, California. He is the chairman of the Computer Science Department since January 1, 2001. From August 1994 to December 1997 he was the Director of the Computer Systems Laboratory at Stanford. From 1979 to 1991 he was on the faculty of the Computer Science Department at Princeton University, Princeton, New Jersey. His research interests include distributed computing systems and database systems. He received a BS in electrical engineering from the Instituto Tecnologico de Monterrey, Mexico, in 1974. From Stanford University, Stanford, California, he received in 1975 a MS in electrical engineering and a PhD in computer science in 1979. Garcia-Molina is a Fellow of the ACM, received the 1999 ACM SIGMOD Innovations Award, and is a member of the President's Information Technology Advisory Committee (PITAC).