Algorithms and Programming Models for Efficient Representation of XML for Internet Applications
NehaNet Corp.
2355 Paragon drive Suite F
San Jose, CA 95131
neel@nehanet.com
NehaNet Corp.
2355 Paragon drive Suite F
San Jose, CA 95131
reshad@nehanet.com
WWW10, May 2-5, 2001, Hong Kong
ACM 1-58113-348-0/01/0005.
ABSTRACT
XML is poised to take the World-Wide-Web to the next level of innovation. XML data, large or small, with or without associated schema, will be exchanged between increasing number of applications running on diverse devices. Efficient storage and transportation of such data is an important issue. We have designed a system called Millau and a series of algorithms for efficient encoding and representation of XML structures. In this paper we describe some of the newer algorithms and APIs in our system for compression of XML structures and data. Our compression algorithms, in addition to separating structure and text for compression, take advantage of the associated schema (if available) in compressing the structure. We also quantify XML documents and their schema with the purpose of defining a decision logic to apply the appropriate compression algorithm for a document or a set of documents following a particular schema. Our system also defines a programming model corresponding to XML DOM and SAX for XML APIs for XML streams and documents in compressed form. Our experiments have shown significant performance gains of our algorithms and APIs. We describe some of these results in this paper. We also describe some web applications based on our system.
Categories and Subject Descriptors
E.4. [Coding and Information Theory]: Data compression and compaction. H.1.1[Systems and Information Theory]: Information theory.
General Terms
Algorithms, Measurement, Performance, Design, Experimentation, Standardization, Languages, Theory.
Keywords
XML, DOM, SAX, Compression, WBXML.
1. INTRODUCTION
With the boom of Business-to-Business applications and the need to run
web applications over a variety of user devices, the Internet community
is rapidly realizing the power of XML [1] as a language
for data communication. The hierarchical structure of the language and
the facility to label and reference elements affords exchanging data while
retaining structural relationship between entities in the data. The extensible
nature of the language with a facility to define domain-specific schemas
(called Document Type Definitions (DTDs) enables customizing the element
and attribute names and their relationships while retaining a common structure.
At the same time, the seamless dependence on the Internet to find information
and conduct business has caused the network bandwidths to be tested to
their limits. One approach to addressing this bandwidth problem is to
compress data on the network.
The Wireless Application Protocol (WAP) [4][9]
defines a format to reduce the transmission size of XML documents with
no loss of functionality or semantic information. The core of our system,
called Millau, extends this format while improving on the compression
algorithm itself. It separates structure compression from text compression.
In addition it takes advantage of the schema and data type information,
if present, to achieve better compression. To be compliant with the XML
standards, it defines APIs equivalent to the tree model of DOM (Document
Object Model) [3] and the event and streaming model
of SAX (Simple API for XML) [2] to work with encoded
XML documents.
This paper discusses new algorithms for efficiently encoding XML documents
in our system. It also discusses quantification of XML documents and their
schema with the purpose of studying these algorithms. It also discusses
programming models and APIs for such efficient representations. The paper
is organized as follows: In the next section we discuss work in text data
compression and XML compression. In section 3 we introduce our system.
In sections 4 and 5 we discuss various improvements to the core compression
algorithm in Millau [22][23].
In section 5, specifically, we discuss the Differential DTD Tree Compression
Algorithm that performs compression based upon the differential information
between the document and its schema. In section 6 we study quantification
of XML documents and DTDs. In section 7 we study experimental results.
In section 8 we discuss Document Object Models that cater to compressed
documents. In section 9 we introduce a couple of prototypical applications
we built using our system. In section 10 we draw conclusions and chalk
out path for future work.
2. RELATED WORK
Lossless data compression is a mature field of research [15]
mainly based on Claude Shannon’s information theory that there
is a direct correlation between the probability of occurrence of a symbol
and the bits needed to encode it. Huffman coding [17]
achieves the minimum amount of redundancy possible in a fixed set of variable
length codes. It uses statistical modeling to encode symbols using the
probability of the symbol’s occurrence. A dictionary based compression
scheme uses a different concept. It looks for groups of data that occur
in a dictionary. If a match is found an index into the dictionary is output
instead of the code for that symbol. The longer the match, the better
the compression ratio. In LZ77 compression [16],
for example, the dictionary consists of all the strings in a window into
the previously read input stream. The deflate algorithm [6]
uses a combination of the LZ77 compression and the Huffman coding. It
is used in popular compression programs like GZIP[7]
or ZLIB [5].
These text compression algorithms perform compression at the character
level. In adaptive extensions (like in LZ77) the system slowly learns
correlations between adjacent pairs, triples, quadruples of characters
to improve upon the compression. Other algorithms [18]
use words instead of characters. In [19] a complete
offline dictionary is inferred to optimize the choice of phrases for optimization.
As for XML, the Wireless Application Protocol Forum [9]
has proposed a table-based encoding of element names and attributes into
what is called a code space. It takes advantage of both the offline approach
(since the codespaces are built offline) and of the word-based approach
(since tags and element names are the most frequent occurrences in an
XML document). However, it does not attempt to compress the text data
and the attribute value data defined outside the DTD that occur in a document.
Moreover, it does not suggest any method to build efficient code spaces.
Our system addresses all of these limitations. Further, it introduces
other compression techniques that are advantageous in certain classes
of XML documents. We quantify XML documents based on various criteria
like complexity (number of elements and attributes, size of the document),
distance from the DTD, and statistical measures like frequency of occurrences
of elements and attributes, size of the text data, tag and text ratios,
and entropy measures based on well-formedness and validity. We measure
DTD complexity based on number and frequency of elements, and density
of the operators, among other measures. We introduce novel algorithms
to perform compression and relate the performances to this quantification.
Other XML-related compression research work includes XMill [25].
XMill uses binary encoding for structure and for content and performs
structure and content separation. Additionally, it takes user input hints
to perform efficient encoding. XMill performs well for large documents
and not so well for smaller documents. XMLZip [24]
from XML Solutions provides a facility for the user to specify the depth
at which compression is to be performed. This way the system provides
efficient access to top-level nodes. The main limitation of XMLZip is
that it consumes large memory resources and runs out of memory for large
documents.
3. COMPRESSION IN Millau
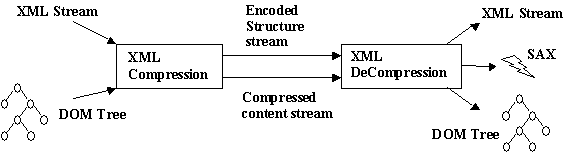
Millau starts with an extensive implementation of WBXML, extending it with separation of structure and content. By separating structure and content it separates the content and structure redundancy by encoding the structure part using the WAP WBXML encoding and the content using standard text compression techniques. Thus the first cut implementation takes advantage of the redundancy in the structure part and of the content part. The general architecture of Millau compression is given in figure 1. The system takes in as input either an XML stream or a DOM tree structure, and as part of compression splits it into 2 parts – a structure part containing the encoding for the element tags and attributes and the content part containing the compressed data form of the text part. The decompression process does just the reverse - - reading in two compressed streams (structure and content) and producing an XML stream or a DOM tree or generating SAX events as required.
3.1 Millau Compression File Format
The Millau encoding format is an extension of the WAP Binary XML format.
The WBXML (Wireless Application Protocol Binary XML) Content Format Specification
[4] defines a compact binary representation of XML.
This format is designed to reduce the transmission size of XML documents
with no loss of functionality or semantic information. For example, WBXML
preserves the element structure of XML, allowing a browser to skip unknown
elements or attributes. More specifically, the WBXML content encodes the
tag names and the attributes names and values with tokens (a token is
a single byte).
In WBXML format, tokens are split into a set of overlapping "code spaces". The meaning of a particular token is dependent on the context in which it is used. There are two classifications of tokens: global tokens and application tokens. Global tokens are assigned a fixed set of codes in all contexts and are unambiguous in all situations. Global tokens are used to encode inline data (e.g., strings, entities, opaque data, etc.) and to encode a variety of miscellaneous control functions. Application tokens have a context-dependent meaning and are split into two overlapping "code spaces": the "tag code space" and the "attribute code space".
The tag code space represents specific tag names. Each tag token is a single-byte code and represents a specific tag name. Each code space is further split into a series of 256 code spaces. Code pages allow for future expansion of the well-known codes. A single token (SWITCH_PAGE) switches between the code pages.
The attribute code space is split into two numeric ranges representing attribute prefixes and attribute values respectively. The Attribute Start token (with a value less than 128) indicates the start of an attribute and may optionally specify the beginning of the attribute value. The Attribute Value token (with a value of 128 or greater) represents a well-known string present in an attribute value. Unknown attribute values are encoded with string, entity or extension codes. All tokenized attributes must begin with a single attribute start token and may be followed by zero or more attribute value, string, entity or extension tokens. An attribute start token, a LITERAL token or the END token indicates the end of an attribute value.
In Millau format, an Attribute Start token is followed by a single Attribute
Value token, string, entity, or extension token. So there is no need to
split the attribute token numeric range into two ranges (less than 128
and 128 or greater) because each time the parser encounters an Attribute
Start token followed by a non-reserved token, it knows that this non-reserved
token is an Attribute Value token and that it can be followed only by
an END token or another Attribute Start token. Thus, instead of two overlapping
code spaces, we have three overlapping code spaces:
1. tag code space as defined in the WAP specification;
2. attribute start code space where each page contains 256 tokens;
3. attribute value code space where each page contains 256 tokens.
Notice that in WBXML format, character data is not compressed. It is
transmitted as strings inline, or as a reference in a string table which
is transmitted at the beginning of the document. In Millau encoding format,
character data can be transmitted on a separate stream. This allows separation
of the content from the structure so that a browser can separately download
the structure and the content or just a part of each. This further allows
compression of the character data using traditional compression algorithms
like deflate [6]. In the structure stream, character
data is indicated by a special global token (STR or STR_ZIP) which indicates
to the Millau parser that it must switch from the structure stream to
the content stream if the user is interested in content and whether the
content is compressed (STR) or uncompressed (STR_ZIP). Optionally, the
length of the content is encoded as an integer in the structure stream
right after the global token (STR_L or STR_ZIP_L). If the length is not
indicated, the strings contained in the structure must terminate with
an End Of String character or a null character.
4. NEW CLASS OF Millau ALGORITHMS
4.1 Improved Code Assignments
The encoding can be improved and better compression can be obtained if the element tags are assigned tokens in such a way that the number of page switches are minimized. One of the techniques would be to break down the elements in the schema based upon proximity of occurrences into clusters whose maximum size is the size of a page.
4.2 Variable Byte Encoding
An alternative to the code spaces approach is to encode the tags with
variable length tokens. One or several bytes encode a tag according to
its occurrence frequency. The 128 most frequent tags will be encoded with
a single byte. The format of these bytes is similar to the byte format
of UTF-8 [20]. The frequency of the element occurrence
can be obtained either by pre-processing the document to identify the
element frequency and assigning smaller tokens for the most frequent ones.
Alternatively, since the DTD represents the document schema, it is possible
to predict the probability of occurrence frequency of each element and
encode based on that. In the most degenerate case, if the DTD has no operators
of the kind ?, *, +, | or ANY, then there is only one single element structure
that is valid for this DTD (though there may be many documents with different
text content, for example). Variable byte encoding can also be driven
by using user input of frequency, or by random assignment of frequencies
to each element.
4.3 Example
Consider the following DTD:
<!ELEMENT book (title, authors, ISBN?, price)> <!ELEMENT title (#PCDATA)> <!ELEMENT authors (author)+> <!ELEMENT author (firstName, lastName)> <!ELEMENT ISBN (#PCDATA)> <!ELEMENT firstName (#PCDATA)> <!ELEMENT lastName (#PCDATA)> <!ELEMENT price (#PCDATA)>
It can be seen from the DTD that the probability of occurrence of the book, title, authors, and price is the same, as they occur exactly once. ISBN occurs zero or one time. For every occurrence of author, there is an occurrence of firstName and of lastName. It can be obviously noted that the probability of occurrence of author is at least as much as that of authors since there is at least one, possibly more than one, occurrence of author. By assigning an upper limit (of say, 5) to the number of occurrences to author, and with the assumption that the number of author occurrences happen with some probability distribution, and by similarly setting the probability of ISBN being present, we can assign probabilities to the occurrence for each element. Then the elements with high probability occurrence are assigned smaller encodings while the elements with low probability occurrences can be assigned longer encodings in the UTF-8 style variable byte encoding scheme. A typical token in this scheme appears as follows:
ABYZZZZZ | YZZZZZZZ | YZZZZZZZ …
where each of X, Y, Z represent a bit and where A is the default flag for content information, B is the default flag for attributes information, Y specifies “has more elements” flag and Z is the token value bit. The Z bits are right aligned and big endian. The following formula is used to determine the number of bytes necessary to encode the number: is given by sup((sup(log v) – 5)/7) + 1; where sup(x) is the smallest integer greater than or equal to x.
4.4 Well-formed Only XML Documents
If the DTD for an XML document is not available, the encoding has to be done on the fly. In this case the correspondence between the tags and tokens has to be done during the compression mechanism. When a new element tag or attribute is encountered, it is sent as plain text with a token assignment, but subsequent occurrence of the same tag is done using this token assignment.
5. DIFFERENTIAL DTD COMPRESSION
As discussed before, a valid XML document refers to its DTD schema and follows its rules. In other words the schema is an approximation of the document. Thus the schema defines knowledge about a document that it knows a-priori. We describe a novel method for compression which encodes only the difference between the schema and the document. Thus the encoding of an XML document is the encoding of the occurrences of its operators like ?, |, +, *. This algorithm can achieve high efficient storage by storing only the minimal structural information.
Example
Consider the DTD given in section 4.3. If we draw the hypothesis that both the sides of the codec (sender and receiver) have prior knowledge of the DTD the only information needed in order to reconstruct the XML document is:
- To know if the ISBN element is chosen inside the book elements.
- To know the number of occurrences of the author elements.
- To separate encoding of PCDATA.
Encoding
The DTD of an XML document can be represented as a tree (similar to the DOM tree), except that that there are specific nodes storing the operators. It is possible to go through that tree, with recursive methods to explore the tree. Our novel algorithm of differential DTD Tree compression (DDT-compression) involves parsing the XML document and the DTD tree simultaneously and following the path of the XML tree inside the DTD tree. This mechanism is similar to a validating parser where the document is parsed and navigated in lock step with the DTD and values for the operators like ?, *, and + are computed. For example, if there is a book document for the DTD in section 4.3 with no ISBN and 3 authors, the value for the ‘?’ operator attached to the book element will be 0 and the value of the ‘+’ operators attached to the author element is 3.
Decoding
The decoding algorithm requires the compressed data and the DTD tree to reconstruct the document. The DTD tree is parsed and each time an operator like *, |, +, ? is encountered the value is read from the document stream. When an element is encountered, it is written to the decompressed XML document. When PCDATA information is expected by the DTD, it is read from the compressed stream.
Implementation Considerations
We use variable byte encoding like UTF-8 to encode element names. For the ‘|’ operator a 1 bit indicates the left branch and a 0 bit indicates the right branch. For ‘*’, and ‘+’ a number is put in the stream indicating the number of occurrences. For ‘?’ a 1 bit indicates presence, and a 0 bit indicates absence. The content part is represented by blocks of data annotated with their respective lengths.
6. QUANTIFICATION OF XML DOCUMENTS AND DTDS
Since XML is the meta-language for all markup documents from small signature documents to large web pages and database structures, the same compression algorithm will not perform uniformly for all types of XML documents. In this section we study the different quantifications of XML document structures that influence or can be used to relate an XML document or its schema to a particular compression algorithm.
General Quantification
General parameters include size of the document in terms of number of elements and in bytes, and the mean and the maximum depth of the XML tree. Statistical measures like distribution of the elements in terms of frequency of their occurrence, standard deviation of the content size and content ratio to the total size of the document, and average number of attributes per element can also be used to study compression algorithms and relate their performance to document properties. A DTD tree can also be quantified using similar measures like number of elements defined in the DTD, depth of the DTD tree, recursion factor (a measure of loops contained in the content model), number of defined attributes, and weighted measure of operators like +, *, |, ? in the DTD. These operators define the flexibility afforded by the DTD and the less flexible it is, the more information it contains, and in return, better compression is achieved.
Distance between the Document and its DTD
The DTD operators give a measure of how specific the DTD is to the document. For instance, a DTD with no operators like +, |, *, or ?, represents unique document structure. The distance between the DTD and a document valid against that DTD can be measured in terms of its operators by giving measures to each of the operators. The distance is the sum of the values assigned to the operators in the DTD. Large DTD distances imply that the DTD does not contain sufficient information about the document and may not enable efficient compression. A more precise measure is obtained using weighted distances. Here the operator values are weighted by the distance of their occurrence from the root of the DTD tree. The deeper the operator occurrences, the greater the weighted distance.
DTD Patterns
Characterizing typical DTD structural patterns can add knowledge to our compression algorithm and in turn help produce efficient encodings. We identify 3 simple patterns which are relevant to the discussions in this paper:
1. The first such structure is the constant structure in which the DTD has no operators (| + * ?) except for ,. For a DTD following this pattern, all corresponding XML documents have exact same structure. They differ only in their PCDATA and attribute values. It can be easily shown that for a constant structure DTD with no PCDATA element, and no attribute, there can be one and only one XML document. A constant structure is represented as constant in a DTD with the following content models:
<!ELEMENT root constant>
Even if the entire DTD is not a constant pattern, a compression algorithm can be aided by identifying elements whose content models form a constant structure since a fixed few tokens can be used to encode the structures.
Consider the following example:
<!ELEMENT root (A, B)> <!ELEMENT A (C*)> <!ELEMENT B (D, E)> <!ELEMENT C (F, G)> <!ELEMENT D (#PCDATA)> <!ELEMENT E (#PCDATA)> <!ELEMENT F (#PCDATA)>
Here the elements root, B, and C have content models that follow the constant pattern. Thus, in a content tree, the constant structures can be encoded using a single encoding rather than encodings for each of the constituents of the structure.
2. The finite pattern represents a finite collection of constant patterns. The finite pattern is one which allows occurrences of only the ? and | operators. Note that a? indicates presence or absence of a and a| b indicates presence of a or presence of b but not both. From a DTD fragment containing only the , ? and | operators it is possible to find all enumerations of possible XML structures.
3. Another type of pattern we identify is a simple list-based database where the root element holds many constant entries. We define this pattern as a first order list pattern. The model is given by:
<!ELEMENT root (entry)* > <!ELEMENT entry constant >
For example: The DTD fragment
<!ELEMENT names (name)*> <!ELEMENT name (firstName,lastName)> <!ELEMENT firstName (#PCDATA)> <!ELEMENT lastName (#PCDATA)>
follows the first order list pattern.
7. COMPARING THE ALGORITHMS
We list the different compression algorithms presented above for convenience.
1. Basic Millau (BM). The original implementation of Millau
encodings.
2. Variable-length Millau (VLM): Variable length encodings in Millau
with random assignments of codes.
3. Variable-length Millau with DTD statistics (VLM-DTD): Tokens
are assigned based upon apriori chosen statistics taken from the DTD.
A tag which has the highest probability of occurrence will have the smallest
length.
4. Variable length Millau with XML statistics (VLM-XML): Same as
3 above except probabilities derived from XML documents directly.
5. DDT Compression (DDT) Differential DTD Tree Compression.
6. ZIP compression (ZIP) (using of standard Java compression package methods).
We compared these algorithms in different dimensions – compression rates, and complexity of the algorithm itself. We ran our experiments using large log files encoded in XML with different number of log structures (Access_log100 with 100 logs and Access_log1000 with 1000 logs), and Shakespeare’s play, Hamlet, encoded in XML.
|
Algorithm |
Encode time (msec) |
Decode time (msec) |
Content size (bytes) |
Structure size (bytes) |
CR % |
|
BM |
914 |
250 |
1222 |
84 |
5.3 |
|
VLM |
266 |
140 |
1222 |
84 |
5.3 |
|
VLM-DTD |
483 |
140 |
1222 |
84 |
5.3 |
|
VLM-XML |
673 |
140 |
1222 |
84 |
5.3 |
|
DDT |
2556 |
293 |
1222 |
38 |
5.1 |
|
GZIP |
3.33 |
3.33 |
1516 |
- |
6.1 |
Table 1 Performance of different Algorithms for Access_log100 with file size = 24528 bytes, content = 41%, structure = 59%, DTD distance = 100. DDT Algorithm obtains the best structure compression but is the slowest. CR is Compression Ratio
|
Algorithm |
Encode time (msec) |
Decode time (msec) |
Content size (bytes) |
Structure size (bytes) |
CR % |
|
BM |
1170 |
1075 |
8819 |
153 |
3.7 |
|
VLM |
813 |
498 |
8819 |
153 |
3.7 |
|
VLM-DTD |
1174 |
510 |
8819 |
153 |
3.7 |
|
VLM-XML |
1278 |
514 |
8819 |
153 |
3.7 |
|
DDT |
7924 |
7934 |
8819 |
39 |
3.6 |
|
GZIP |
77 |
70 |
10457 |
- |
4.3 |
Table 2 Performance of different Algorithms for Access_log1000 with file size = 244655 bytes, content = 42%, structure = 58%, DTD distance = 1000. DDT Algorithm obtains the best structure compression but is the slowest.
|
Algorithm |
Encode time (msec) |
Decode time (msec) |
Content size (bytes) |
Structure size (bytes) |
CR % |
|
BM |
1511 |
861 |
71349 |
1292 |
25.2 |
|
VLM |
1127 |
501 |
71349 |
1292 |
25.2 |
|
VLM-DTD |
1625 |
471 |
71349 |
1292 |
25.2 |
|
VLM-XML |
1692 |
471 |
71349 |
1292 |
25.2 |
|
DDT |
N/A |
N/A |
N/A |
N/A |
N/A |
|
GZIP |
235 |
201 |
79931 |
- |
27.6 |
Table 3 Performance of different Algorithms for Hamlet with file size = 288735 bytes, content = 60%, structure = 40%, DTD distance = 2771. DDT Algorithm performs poorly (exceeds our performance threshold), because of the significant difference between DTD distance (2771) and weighted DTD distance (51140432)
Large Web XML log files are standard Web log files encoded in XML. The data is well-formed and valid against its DTD. For this DTD the weighted distance is low. Each log entry element follows a constant architecture (has no operators like ?,|,*,+). The DTD itself follows the first order list pattern. Web log files tend to have high redundancy in both content and text. Such files are representative of large XML database files like addresses and bibliography. The hamlet.xml DTD has operators like ?, |, *, + buried deep, thus making the weighted distance large as compared to the DTD distance measure.
It can be seen that DDT compression achieves significant structural compression.
In the case of Access_log100.xml (see Table 1) and
Access_log1000.xml (see Table 2), DDT compression
achieves over 2.7 times and 4 times better compression of structure. In
case of hamlet.xml (see Table 3), since the DTD distance
is 2771 and the weighted DTD distance 51140332, the wide difference between
the two causes DDT compression to be inefficient. Our experiment with
DDT compression exceeded the default memory and time settings we had in
the experiment due to extensive recursion. The difference in the distance
implies the operators being away from the root element. DDT compression
does not perform well in such cases. Thus, for DDT compression to perform
well, the DTD distance should be large but not the weighted distance,
i.e., the operators should be close to the root. The optimal case would
occur when the weighted distance equals the DTD (standard) distance.
7.1 Content Grouping
With data redundance at nodes of the same level content grouping can
help improve compression. Content grouping basically reorders the content
of a document to group similar element structures or elements with the
same names together. A similar approach is taken in relational databases
where column-wise compression achieves better compression than row-wise
compression [25]. Traditional compression algorithms
that use compression windows can take advantage of this re-organization.
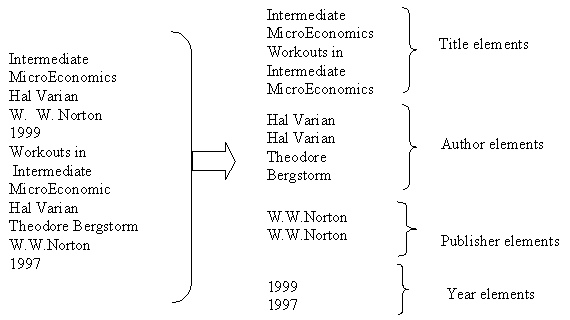
Consider the example in figure 2. The document on the left shows 2 bibliographical entries in XML form. The document on the right shows the extracted structure part of the document on the left. The content part is shown in figure 3.
Figure 2 Content and structure separation: The left box shows the original document. The right box shows the structure with references to the content. Content part is shown in figure 3.
Figure 3 Similar content grouping: By reordering the structure and grouping to gether the content under similar structures traditional text compression algorithms like LZ77 can perform better.
Content under similar element structures are grouped together. By reordering
the structure and grouping together content under similar structures,
traditional text compression algorithms like LZ77 can perform better.
Content grouping, however, has the overhead of multiplexing between different
content streams and to see the advantage of grouping of similar items
requires the document size to exceed a threshold. For Web log files of
size under the threshold of 9K bytes content grouping performs 5 to 10
percent poorer than standard Millau compression. Studying the numbers
in the dimension of tag occurrences, as the tag occurrences go up (and
so do the text content under them), we saw up to 20% improvement in the
compressed size. The gain of using content grouping is described by a
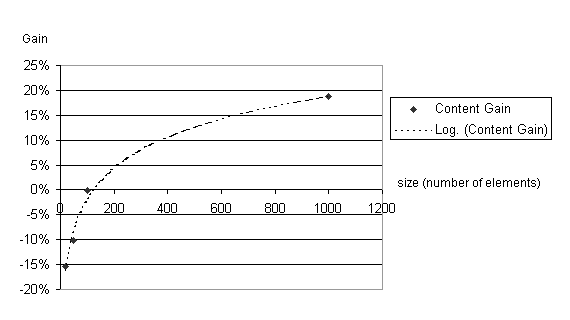
logarithmic increase as the size of the document increases. Over the threshold
of 9K elements, content grouping improves compression size in a logarithmic
way (see Figure 4).
Figure 4 Logarithmic trend of the content grouping gain. Beyond a threshold (100 element structures) the content grouping helps in improving the content compression.
7.2 Compression Speed
All of our algorithms are implemented in Java. Due to Java performance limitations, they perform slower than known C or C++ implementations. Within the variations of the algorithms implemented in Java, DDT compression is the slowest.
7.3 Composed Algorithm
Since different algorithms perform differently on different size and
types of XML documents we came up with a composed algorithm that applies
some decision logic before picking the appropriate encoder. The decision
logic works as follows (see Figure 5). If the document
is not wellformed, standard ZIP compression is applied. If it is well
formed, then if DTD information is not present, then Well-formed Millau
is applied. If DTD information is available, weighted DTD distance and
standard DTD distance is computed and compared. If the difference between
the two is large, variable byte Encoding Millau compression is
chosen. Otherwise, DDT compression is chosen. For documents of size more
than 10k content grouping is activated. When variable byte encoding Millau
is chosen, if the number of elements in the DTD is more than 255 then
enhanced Millau with DTD statistics is chosen, otherwise, enhanced
Millau with random statistics is chosen.
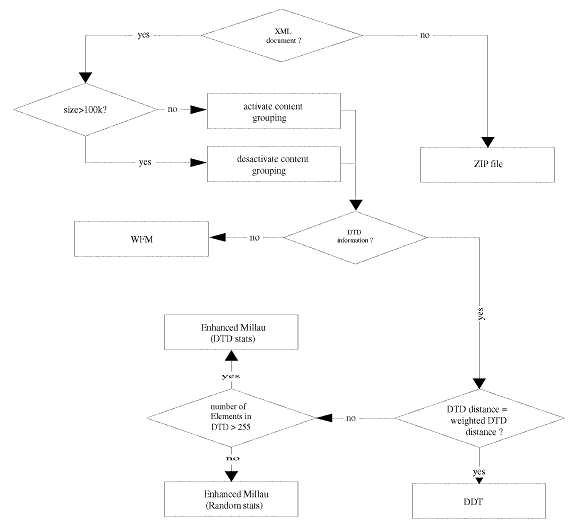
Figure 5 Flowchart of decision algorithm for picking the right compression algorithm based upon the characteristics of the XML document and its associated DTD (if present)
We implemented this composed decision algorithm and found that on an average the decision process caused an overhead of under 4% in size over the optimal algorithm (the optimal algorithm is chosen a posteriori after trying all the algorithms.)
8. EFFICIENT DOCUMENT OBJECT MODELS
The XML standard includes a document object model called DOM that allows navigating, querying, and updating a parsed XML document tree. Typical DOM implementations are in-memory tree based (which means that the whole XML tree is constructed in memory for full processing), though variants like Lazy DOM, Persistent DOM [27] have emerged that take load documents into memory in a delayed fashion. In addition to DOM, Simple API for XML (SAX) provides a programming interface that enables streaming XML and is event-driven. In this section we study how compression and encoding can influence this API definition.
8.1 Document Object Models for Encoded Documents
The DOM model mainly caters to the assumption that the underlying document tree has character and not binary encoding. Even though most of the DOM API methods can be implemented to support compressed encodings some additional methods are required to enhance and take advantage of the fact that the document is encoded. The DOM API methods use element and attribute names as arguments or results. The first generation Millau extends these APIs to support BDOM (Binary DOM) by allowing lookup and return using tokens, instead. Our SAX parser supports event-based parsing in SAX. Further, SAX is extended to support encodings instead of string names in the SAX API methods. The DOM and SAX support helps avoid conversion between binary encoded and compressed XML documents and the ASCII form unnecessarily for the sake of supporting DOM and SAX. In our experiments, for a sample document of size 3MB, standard parsing took 40 seconds; the same document compressed using Millau and using our SAX parser took 8 seconds; with our binary SAX parser it took 5 seconds.
8.2 Schema-aware Document Object Models
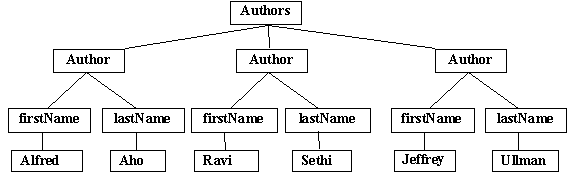
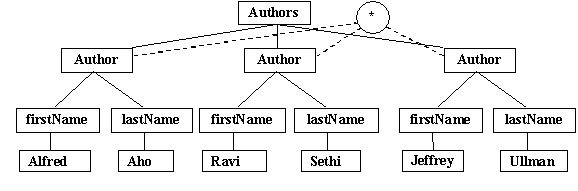
Validating XML parsers have to parse two documents – the content document that is being validated and parsed; and the schema document against which this document is validated. DDT compression operates in a manner similar to a validating XML parser in that it looks for the differential between the document and the schema to obtain better encoding. One method to make this process efficient is to encode schematic information in the nodes of the document itself. Corresponding to DOM we define a Schema-driven DOM or SDOM model where the non-constant operator information like *, |, ?, +, are stored within the nodes in the DOM tree. For example, consider the DTD in section 4.3. Consider a DOM tree fragment rooted at the authors element. The DOM tree is illustrated by Figure 6.
From the tree it is not apparent that the schema of the Authors element is Author* and not Author, Author, Author or something else. By decorating the tree with the schema of Authors we get a SDOM tree which looks like Figure 7.
Figure 7 The Schema-driven DOM (SDOM) tree corresponding to the DOM tree in figure 6. The original DOMtree is decorated with the ‘*’ operator indicating that the content model for Authors is Author*. The rest of the tree is not decorated since the content model model follows the constant pattern.
In the DOM model, all the programming interfaces corresponding to the different entities in XML like Element, Attribute, Comment, Entity, PI, etc. are derived from a base Node interface. We extend the NODE interface for SDOM. The base interface for SDOM is called the SPNode interface. There are three derivations of this interface – XNode (element Node in SDOM), OPNode (operator node), and CLNode (Cluster node denoting a group of nodes separated by a ‘,’ in the DTD). Correspondingly, new methods are added in SDOM to setting and getting the operators associated with a Node object and setting and getting the size of a cluster of nodes. We describe these methods below.
XNode Methods:
| void setElement(Node) | set the associated element |
| Node getElement() | get the associated element |
| void setUnderlying(Node) | set the SDOM tree under this node |
| Node getUnderlying(Node) | get the SDOM tree underlying this node |
OPNode Methods:
| void addNode(Node node) | add a node in the subtree of this operator |
| int getSize(Node node) | get the number of SPNodes under this OPNode |
| SPNode getNode(int index) | get the index-th SPNode under this OPNode |
| int getType() | get the type of the operator (*, +, ? or |) |
| void setType(int type) | set the type of the operataor (*, +, ? or |) |
CLNode Methods:
| void addNode(Node node) | add a node to the subtree of the cluster node |
| int getSize() | get the number of children of this cluster node |
| Node getNode(int index) | get the index-th node of this cluster node |
8.2.1 SXML Documents
Corresponding to the SDOM model there is a textual representation of XML. We call this the Schema-driven XML or SXML document. An SXML document is an XML document with extended markup to represent the DTD structure inside the document. We use the XML Processing Instruction (PI) facility to embed the schema information into the document. This way we retain the XML validity of the original document against its DTD while enhancing it with Processing Instructions about the schema. Processing Instructions in XML are like Pragmas in standard programming languages. We introduce two types of PIs -- one for operators, and the other for clusters.
PI for Operators
Operators have the following format:
<?SXML “start-operator” “operator” [“count”]> … <?SXML “end-operator”>
where “operator” can be one of - *, +, ?, or | . “count” represents the number of occurrences for that operator (applicable to only * and +). For example,
<?SXML “start-operator” “*” “3”> <x/> <?SXML “end-operator”>
denotes the 3 repeated occurrences of the element x corresponding to the content model x*.
PI for Clusters
<?SXML “start-cluster” “count”> … <?SXML “end-cluster”>
where count is the number of Elements inside the cluster node.
The schema for SXML itself can be expressed as an extension to that of the underlying XML using the following production rules:
SXML => (XML|Cluster)*
Cluster => (XML|Cluster|Operator)*
Operator => (XML|Cluster)*
The SXML fragment corresponding to the SDOM tree discussed in section 8.2. is illustrated by the following.
<authors>
<?SXML “start-operator” “*’ “3”>
<author>
<firstName>Alfred</firstName>
<lastName>Aho</lastName>
</author>
<author>
<firstName>Alfred</firstName>
<lastName>Aho</lastName>
</author>
<author>
<firstName>Alfred</firstName>
<lastName>Aho</lastName>
</author>
<?SXML “end-operator”>
</authors>
8.3 Programming Interface for SXML
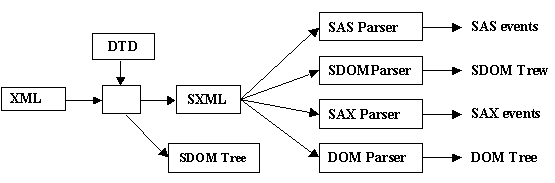
Analogous to the DOM and SAX programming models for standard XML, for the SXML document structure, we have Schema-driven DOM (SDOM) and Schema-driven SAX (SAS). Figure 8 shows the conceptual relationship between the XML, DTD, DOM, SAX, SDOM, and SAS. Given an XML document and its DTD, our parser can create an SDOM tree or create an SXML document as output. On this SXML document a DOM parser can produce a DOM tree, a SAX parser can generate SAX events, an SDOM parser can produce an SDOM tree, and a SAS parser can produce SAS events.
Figure 8 SDOM/SXML general architecture. From an XML document and its DTD, our parser can create an SDOM tree or an SXML document as output. The SXML document can be run through a DOM parser (to create a DOM tree), a SAX parser ( to generate SAX events), or an SDOM parser (to generate an SDOM tree) or a SAS parser (to generate SAS events).
8.4 Use of SDOM and SXML
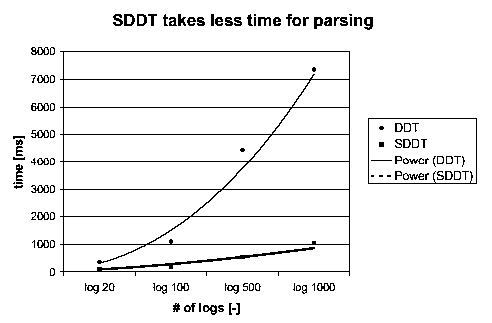
As we have already seen, SDOM and SXML can be used for the purposes of achieving better XML compression using the Differential DTD Tree algorithm. Compression using the SDOM tree is faster than the one using the DOM tree because we do not need to parse the DTD separately. We performed experiments with the SDOM-based DDT compression (called the SDDT compression algorithm) and found that over 80% faster than our original DDT compression. This compensates for the slowness of DDT algorithm as seen in tables 1, 2, and 3. Figure 9 shows a graph of the time taken for parsing log files in XML syntax of varying sizes. From the figure it can be seen that as the size of the file increases, SDDT performs increasingly better as compared to DDT.
In addition, SXML documents enable faster validating parsers than typical XML documents as the schema is closely associated with the content. SDOM can also be used for better and faster application processing of XML data. SDOM data is more structured and allow easy measurement of content than regular XML. This allows faster parsing, validation and analysis of XML data.
We can think of further ameliorations to SDOM and SXML implementations. The first improvement is the use of compression inside the SDOM tree to reduce memory usage. Another improvement is to use tokens instead of tags inside the SDOM tree as well as using caching for content to disk instead of memory.
Figure 9 SDDT compression performs much better than DDT compression for the Access log files of different sizes. As the file size increases, SDDT performs increasingly better.
In summary, SDOM and SXML provide a new way of associating schema with XML content. This improvement opens doors for faster compression and content processing. The SDOM structure as we have designed and implemented it is backward compatible with the standard DOM model. Similarly, SXML is XML with additional schematic annotations. The downside of associating the schema with the document this way is the increase in the document size. More importantly, changes in the DTD have to be appropriately reflected into the SXML document.
9. Applications
We have built two prototypical applications using our model of XML compression.
9.1 Compression-Decompression Proxy Server Application
Proxy servers have been used to efficiently tokenize HTML pages to reduce
network bandwidth. Significant work has been done to reduce network bandwidth
by using Proxy servers to efficiently compress and decompress data over
the network [11]. However, they do not have a systematic
way to compress arbitrary XML documents.
In the architecture of our prototypical system we have two proxy servers:
a server-side proxy server, and a client-side proxy server. Our proxy
servers were built using the WBI (Web Intelligence), a programmable proxy
server package [15]. An XML request from a client
(say a browser) is intercepted by the client proxy server, compressed
and sent to the server. On the server side it is intercepted by the server-side
proxy server and decompressed before sending it to the actual server.
Similarly, the response from the server is compressed by the server-side
proxy server and sent to the client to be intercepted by the client-side
proxy server to be decompressed and served to the client.
For typical documents, our system is 4 times faster. For transmission of small documents with approximately 20% compression-decompression overhead, it reduces the document size from an average of 3647 bytes to an average of 886 bytes. For a large document of average size 213 Kb our system reduces the transmission time from 30 seconds to 21 seconds where the document is compressed to an average size of 148Kb. There is an overhead of 1.5 seconds.
9.2 XML-based RPC Mechanism
XML-RPC [11] is used for remote procedure calls over HTTP using XML. An XML-RPC message is an HTTP-POST request. The body of the request is in XML. A procedure executes on the server and the value it returns is also formatted in XML. Procedure parameters can be scalars, numbers, strings, dates, etc., and can also be complex record and list structures. In our implementation, the body of the request is encoded using our compression scheme. To evaluate the performance of this implementation, we made a benchmark which sends an array of 100 integers as a parameter and receives the same array as a return value. We compared the performances of our implementation with the Helma XML-RPC system [12]. Helma RPC system could do 12 RPC calls per second. Using our system, we could do 27 RPC calls per second once again proving its compression efficiency.
10. Conclusions and Future Work
As XML becomes pervasive in Internet applications, new methods for efficiently storing, streaming, and processing XML structures will be required. The contributions of this paper are three-fold: We described a number of novel compression algorithms in the context of our system for XML. We used XML and DTD quantification to study and compare these algorithms. We also introduce novel programmatic APIs for XML that can take advantage of our compression-decompression schemes. We also looked at 2 prototypical applications of our system. As we write, we continue to improve our algorithms and study their performance on various classes of XML documents. We have also built a variation of the DDT compression called the DTD Constant Structures compression (or DCS compression) where we look for the largest constant structures within the DTD and encode them with efficiently and achieve better compression. As we continue to benchmark our system, we will also look at new applications that can use our algorithms.
Another area of work we continue to research is lazy loading of XML documents into memory. This is motivated by the fact that exploitation of large XML documents can become extremely difficult for regular applications if the data has to be modeled in memory (like for DOM). XML compression can be useful for storing and accessing this data without decompressing the full data or storing it in memory. DDT-compression can help achieve of such applications. In DDT-compressed data, both the structure and content are accessible without first decompressing the data. This is due to the small structural information stored in DDT-compression which can be easily decompressed. Then content data can be accessed randomly without decompressing the whole data, requiring only small memory overhead. This model of XML processing has interesting applications in streaming XML structures over the network medium.
The authors acknowledge Marc Girardot who implemented the first version
of Millau. Part of this was the second author’s thesis [27]
work done at the IBM Almaden Research Center.
11. REFERENCES
[1] Extensible Markup Language (XML) 1.0, W3C Recommendation 10-Feb 1998, http://www.w3.org/TR/REC-xml
[2] SAX 1.0: The Simple API for XML, http://www.megginson.com/SAX/
[3] Document Object Model (DOM) Level 1 Specification Version 1.0, W3C Recommendation 1 October, 1998, http://www.w3.org/TR/REC-DOM-Level-1/
[4] WAP Binary XML Content Format, W3C NOTE 24 June 1999, http://www.w3.org/TR/wbxml/
[5] P. Deutsch, J. Gailly, "ZLIB Compressed Data Format Specification Version 3.3", RFC 1950, May 1996, http://www.ietf.org/rfc/rfc1950.txt
[6] P. Deutsch, "DEFLATE Compressed Data Format Specification version 1.3", RFC 1951, Aladdin Enterprises, May 1996, http://www.ietf.org/rfc/rfc1951.txt
[7] P. Deutsch, "GZIP file format specification version 4.3", RFC 1952, Aladdin Enterprises, May 1996, http://www.ietf.org/rfc/rfc1952.txt
[8] J. Bosak. Shakespeare's plays encoded in XML http://metalab.unc.edu/bosak/xml/eg/shaks200.zip
[9] The Wireless Application Protocol (WAP) Forum, http://www.wapforum.org/
[10] J.C. Mogul, F. Douglis, A. Feldmann, B. Krishnamurthy, "Potential benefits of delta-encoding and data compression for HTTP", Proceedings of the ACM SIGCOMM '97 Conference, September 1997
[11] XML-RPC Home Page: http://www.xml-rpc.com/
[12] Hannes Wallnöfer, XML-RPC Library for Java, http://helma.at/hannes/xmlrpc/
[13] Open Applications Group, http://www.openapplications.org/
[14] Rob Barrett, Paul Maglio, Jöerg Meyer, Steve Ihde, and Stephen Farrell, WBI Development Kit, http://www.alphaworks.ibm.com/tech/wbidk
[15] M. Nelson, The Data Compression Book, M&T Books, 1992
[16] J. Ziv, and A. Lempel, "A universal algorithm for sequential data compression", IEEE Transaction on Information Theory, Volume 23, Number 3, May 1997, pages 337-343
[17] D.A.Huffman., "A method for the construction of minimum-redundancy codes", Proceedings of the IRE, Volume 40, Number 9, September 1952, pages 1098-1101
[18] R. Nigel Horspool, Gordon V. Cormack, "Constructing Word-Based Text Compression Algorithms", IEEE Transaction on Information Theory, 1992
[19] N. Jesper Larsson, Alistair Moffat, "Offline Dictionary-Based Compression", IEEE Transaction on Information Theory, 1999
[20] F. Yergeau, "UTF-8, a transformation format of ISO 10646", RFC 2279, Alis Technologies, January 1998, http://www.ietf.org/rfc/rfc2279.txt
[21] IBM XML Parser for Java, http://www.alphaworks.ibm.com/tech/xml4j
[22] M. Girardot, N. Sundaresan, "Efficient representation and streaming of XML content over the Internet medium", IEEE International Conference on Multimedia and Expo 2000, New York, July 2000.
[23] M. Girardot, N. Sundaresan. “Millau: an encoding format for efficient representation and exchange of XML over the Web”, Proceedings of the 9th WWW Conference, May 2000, Amsterdam, Netherlands.
[24] XML Solutions. XMLZip, available from http://www.xmls.com/products/xmlzip/xmlzip.html
[25] H. Liefke, D. Suciu. XMILL: An Efficient Compressor for XML Data. ACM SIGMOD 2000. Dallas, Texas.
[26] B. Iyer and D. Wilhite. Data Compression Support in Databases. Proceedings of the 20th International Conference on Very Large Databases. Pp 695-704. Santiago, Chile, 1994.
[27] R. Moussa. XML Data Compression, Quantification, and Representation. Thesis Report. Multimedia Communications, Eurecom Institute. Sofia Antipolis, France. July 2000.
[28] I. Macherius. Java Applications: XQL Language and Persistent W3C-DOM. http://www.oasis-open.org/cover/macherius19990329.html
12. BIOGRAPHY
Dr. Neel Sundaresan is a co-founder and Chief Technology Officer of NehaNet Corporation, a company focusing on Intelligent Electronic Commerce. Prior to this he was a research manager of the eMerging Internet Technologies department at the IBM Almaden Research Center. He has been IBM since December 1995 and has pioneered several XML and internet related research projects. He was one of the chief architects of the Grand Central Station project at IBM Research for building XML-based search engines. He received his PhD in CS in 1995. He has done research and advanced technology work in the area of Compilers and Programming Languages, Parallel and Distributed Systems and Algorithms, Information Theory, Data Mining and Semi-structured Data, Speech Synthesis, Agent Systems, and Internet and Electronic Commerce Systems. He has authored over 40 research publications and has given several invited and refereed talks and tutorials at national and international conferences. He is a frequent speaker at user groups and industrial conferences. He has been a member of the W3C standards effort.
Reshad Moussa is a Member of Technical Staff at NehaNet Corporation. He holds a Masters degree in computier science in the Multimedia major from the EPFL (Switzerland). He also did research and development work at the IBM Almaden center on XML technologies. His areas of research interests and expertise include Multimedia, Information Theory, Fractals, Usability Engineering, Security, and Internet technologies with focus on XML.