Basics of Caffe2 - Workspaces, Operators, and Nets
This tutorial introduces a few basic Caffe2 components:
- Workspaces
- Operators
- Nets
You also may want to review the Intro Tutorial before starting this notebook.
In this tutorial we will go through a set of Caffe2 basics: the basic concepts including how operators and nets are being written.
First, let’s import caffe2. core and workspace are usually the two that you need most. If you want to manipulate protocol buffers generated by caffe2, you probably also want to import caffe2_pb2 from caffe2.proto.
1 2 3 4 5 6 7 8 9 10 | # We'll also import a few standard python libraries from matplotlib import pyplot import numpy as np import time # These are the droids you are looking for. from caffe2.python import core, workspace from caffe2.proto import caffe2_pb2 # Let's show all plots inline. %matplotlib inline |
You might see a warning saying that caffe2 does not have GPU support. That means you are running a CPU-only build. Don’t be alarmed - anything CPU is still runnable without problem.
Workspaces
Let’s cover workspaces first, where all the data reside.
If you are familiar with Matlab, workspace consists of blobs you create and store in memory. For now, consider a blob to be a N-dimensional Tensor similar to numpy’s ndarray, but is contiguous. Down the road, we will show you that a blob is actually a typed pointer that can store any type of C++ objects, but Tensor is the most common type stored in a blob. Let’s show what the interface looks like.
Blobs() prints out all existing blobs in the workspace.
HasBlob() queries if a blob exists in the workspace. For now, we don’t have anything yet.
1 2 | print("Current blobs in the workspace: {}".format(workspace.Blobs())) print("Workspace has blob 'X'? {}".format(workspace.HasBlob("X"))) |
We can feed blobs into the workspace using FeedBlob().
1 2 3 | X = np.random.randn(2, 3).astype(np.float32) print("Generated X from numpy:\n{}".format(X)) workspace.FeedBlob("X", X) |
1 2 3 | Generated X from numpy: [[-0.56927377 -1.28052795 -0.95808828] [-0.44225693 -0.0620895 -0.50509363]] |
Now, let’s take a look what blobs there are in the workspace.
1 2 3 | print("Current blobs in the workspace: {}".format(workspace.Blobs())) print("Workspace has blob 'X'? {}".format(workspace.HasBlob("X"))) print("Fetched X:\n{}".format(workspace.FetchBlob("X"))) |
1 2 3 4 5 | Current blobs in the workspace: [u'X'] Workspace has blob 'X'? True Fetched X: [[-0.56927377 -1.28052795 -0.95808828] [-0.44225693 -0.0620895 -0.50509363]] |
Let’s verify that the arrays are equal.
1 | np.testing.assert_array_equal(X, workspace.FetchBlob("X")) |
Also, if you are trying to access a blob that does not exist, an error will be thrown:
1 2 3 4 | try: workspace.FetchBlob("invincible_pink_unicorn") except RuntimeError as err: print(err) |
1 | [enforce fail at pybind_state.cc:441] gWorkspace->HasBlob(name). |
One thing that you might not use immediately: you can have multiple workspaces in Python using different names, and switch between them. Blobs in different workspaces are separate from each other. You can query the current workspace using CurrentWorkspace. Let’s try switching the workspace by name (gutentag) and creating a new one if it doesn’t exist.
1 2 3 4 5 6 7 8 9 10 11 | print("Current workspace: {}".format(workspace.CurrentWorkspace())) print("Current blobs in the workspace: {}".format(workspace.Blobs())) # Switch the workspace. The second argument "True" means creating # the workspace if it is missing. workspace.SwitchWorkspace("gutentag", True) # Let's print the current workspace. Note that there is nothing in the # workspace yet. print("Current workspace: {}".format(workspace.CurrentWorkspace())) print("Current blobs in the workspace: {}".format(workspace.Blobs())) |
1 2 3 4 | Current workspace: default Current blobs in the workspace: ['X'] Current workspace: gutentag Current blobs in the workspace: [] |
Let’s switch back to the default workspace.
1 2 3 | workspace.SwitchWorkspace("default") print("Current workspace: {}".format(workspace.CurrentWorkspace())) print("Current blobs in the workspace: {}".format(workspace.Blobs())) |
1 2 | Current workspace: default Current blobs in the workspace: ['X'] |
Finally, ResetWorkspace() clears anything that is in the current workspace.
1 | workspace.ResetWorkspace() |
Operators
Operators in Caffe2 are kind of like functions. From the C++ side, they all derive from a common interface, and are registered by type, so that we can call different operators during runtime. The interface of operators is defined in caffe2/proto/caffe2.proto. Basically, it takes in a bunch of inputs, and produces a bunch of outputs.
Remember, when we say “create an operator” in Caffe2 Python, nothing gets run yet. All it does is to create the protocol buffer that specifies what the operator should be. At a later time it will be sent to the C++ backend for execution. If you are not familiar with protobuf, it is a json-like serialization tool for structured data. Find more about protocol buffers here.
Let’s see an actual example.
1 2 3 4 5 6 7 | # Create an operator. op = core.CreateOperator( "Relu", # The type of operator that we want to run ["X"], # A list of input blobs by their names ["Y"], # A list of output blobs by their names ) # and we are done! |
As we mentioned, the created op is actually a protobuf object. Let’s show the content.
1 2 3 | print("Type of the created op is: {}".format(type(op))) print("Content:\n") print(str(op)) |
1 2 3 4 5 6 7 | Type of the created op is: <class 'caffe2.proto.caffe2_pb2.OperatorDef'> Content: input: "X" output: "Y" name: "" type: "Relu" |
OK, let’s run the operator. We first feed in the input X to the workspace.
Then the simplest way to run an operator is to do workspace.RunOperatorOnce(operator)
1 2 | workspace.FeedBlob("X", np.random.randn(2, 3).astype(np.float32)) workspace.RunOperatorOnce(op) |
After execution, let’s see if the operator is doing the right thing, which is our neural network’s activation function (Relu) in this case.
1 2 3 4 | print("Current blobs in the workspace: {}\n".format(workspace.Blobs())) print("X:\n{}\n".format(workspace.FetchBlob("X"))) print("Y:\n{}\n".format(workspace.FetchBlob("Y"))) print("Expected:\n{}\n".format(np.maximum(workspace.FetchBlob("X"), 0))) |
1 2 3 4 5 6 7 8 9 10 11 12 13 | Current blobs in the workspace: ['X', 'Y'] X: [[ 1.03125858 1.0038228 0.0066975 ] [ 1.33142471 1.80271244 -0.54222912]] Y: [[ 1.03125858 1.0038228 0.0066975 ] [ 1.33142471 1.80271244 0. ]] Expected: [[ 1.03125858 1.0038228 0.0066975 ] [ 1.33142471 1.80271244 0. ]] |
This is working if you’re expected output matches your Y output in this example.
Operators also take optional arguments if needed. They are specified as key-value pairs. Let’s take a look at one simple example, which is to create a tensor and fills it with Gaussian random variables.
1 2 3 4 5 6 7 8 9 10 | op = core.CreateOperator( "GaussianFill", [], # GaussianFill does not need any parameters. ["Z"], shape=[100, 100], # shape argument as a list of ints. mean=1.0, # mean as a single float std=1.0, # std as a single float ) print("Content of op:\n") print(str(op)) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Content of op:
output: "Z"
name: ""
type: "GaussianFill"
arg {
name: "std"
f: 1.0
}
arg {
name: "shape"
ints: 100
ints: 100
}
arg {
name: "mean"
f: 1.0
}
|
Let’s run it and see if things are as intended.
1 2 3 4 | workspace.RunOperatorOnce(op) temp = workspace.FetchBlob("Z") pyplot.hist(temp.flatten(), bins=50) pyplot.title("Distribution of Z") |
1 | <matplotlib.text.Text at 0x7f2bd2d51710> |
If you see a bell shaped curve then it worked!
Nets
Nets are essentially computation graphs. We keep the name Net for backward consistency (and also to pay tribute to neural nets). A Net is composed of multiple operators just like a program written as a sequence of commands. Let’s take a look.
When we talk about nets, we will also talk about BlobReference, which is an object that wraps around a string so we can do easy chaining of operators.
Let’s create a network that is essentially the equivalent of the following python math:
1 2 3 4 | X = np.random.randn(2, 3) W = np.random.randn(5, 3) b = np.ones(5) Y = X * W^T + b |
We’ll show the progres step by step. Caffe2’s core.Net is a wrapper class around a NetDef protocol buffer.
When creating a network, its underlying protocol buffer is essentially empty other than the network name. Let’s create the net and then show the proto content.
1 2 | net = core.Net("my_first_net") print("Current network proto:\n\n{}".format(net.Proto())) |
1 2 3 | Current network proto: name: "my_first_net" |
Let’s create a blob called X, and use GaussianFill to fill it with some random data.
1 2 | X = net.GaussianFill([], ["X"], mean=0.0, std=1.0, shape=[2, 3], run_once=0) print("New network proto:\n\n{}".format(net.Proto())) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | New network proto:
name: "my_first_net"
op {
output: "X"
name: ""
type: "GaussianFill"
arg {
name: "std"
f: 1.0
}
arg {
name: "run_once"
i: 0
}
arg {
name: "shape"
ints: 2
ints: 3
}
arg {
name: "mean"
f: 0.0
}
}
|
You might have observed a few differences from the earlier core.CreateOperator call. Basically, when we have a net, you can direct create an operator and add it to the net at the same time using Python tricks: essentially, if you call net.SomeOp where SomeOp is a registered type string of an operator, this essentially gets translated to
1 2 | op = core.CreateOperator("SomeOp", ...)
net.Proto().op.append(op)
|
Also, you might be wondering what X is. X is a BlobReference which basically records two things:
- what its name is. You can access the name by str(X)
- which net it gets created from. It is recorded by an internal variable
_from_net, but most likely you won’t need that.
Let’s verify it. Also, remember, we are not actually running anything yet, so X contains nothing but a symbol. Don’t expect to get any numerical values out of it right now :)
1 2 | print("Type of X is: {}".format(type(X))) print("The blob name is: {}".format(str(X))) |
1 2 | Type of X is: <class 'caffe2.python.core.BlobReference'> The blob name is: X |
Let’s continue to create W and b.
1 2 | W = net.GaussianFill([], ["W"], mean=0.0, std=1.0, shape=[5, 3], run_once=0) b = net.ConstantFill([], ["b"], shape=[5,], value=1.0, run_once=0) |
Now, one simple code sugar: since the BlobReference objects know what net it is generated from, in addition to creating operators from net, you can also create operators from BlobReferences. Let’s create the FC operator in this way.
1 | Y = X.FC([W, b], ["Y"]) |
Under the hood, X.FC(...) simply delegates to net.FC by inserting X as the first input of the corresponding operator, so what we did above is equivalent to
1 | Y = net.FC([X, W, b], ["Y"]) |
Let’s take a look at the current network.
1 | print("Current network proto:\n\n{}".format(net.Proto())) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 | Current network proto:
name: "my_first_net"
op {
output: "X"
name: ""
type: "GaussianFill"
arg {
name: "std"
f: 1.0
}
arg {
name: "run_once"
i: 0
}
arg {
name: "shape"
ints: 2
ints: 3
}
arg {
name: "mean"
f: 0.0
}
}
op {
output: "W"
name: ""
type: "GaussianFill"
arg {
name: "std"
f: 1.0
}
arg {
name: "run_once"
i: 0
}
arg {
name: "shape"
ints: 5
ints: 3
}
arg {
name: "mean"
f: 0.0
}
}
op {
output: "b"
name: ""
type: "ConstantFill"
arg {
name: "run_once"
i: 0
}
arg {
name: "shape"
ints: 5
}
arg {
name: "value"
f: 1.0
}
}
op {
input: "X"
input: "W"
input: "b"
output: "Y"
name: ""
type: "FC"
}
|
Too verbose huh? Let’s try to visualize it as a graph. Caffe2 ships with a very minimal graph visualization tool for this purpose. Let’s show that in ipython.
1 2 3 4 | from caffe2.python import net_drawer from IPython import display graph = net_drawer.GetPydotGraph(net, rankdir="LR") display.Image(graph.create_png(), width=800) |
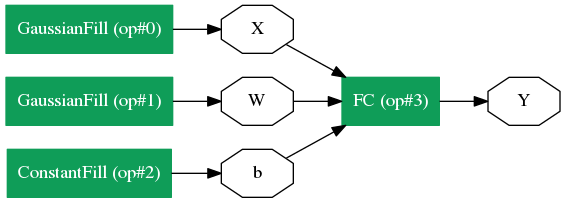
So we have defined a Net, but nothing gets executed yet. Remember that the net above is essentially a protobuf that holds the definition of the network. When we actually want to run the network, what happens under the hood is:
- Instantiate a C++ net object from the protobuf;
- Call the instantiated net’s Run() function.
Before we do anything, we should clear any earlier workspace variables with ResetWorkspace().
Then there are two ways to run a net from Python. We will do the first option in the example below.
- Using
workspace.RunNetOnce(), which instantiates, runs and immediately destructs the network. - A little bit more complex and involves two steps:
(a) call
workspace.CreateNet()to create the C++ net object owned by the workspace, and (b) useworkspace.RunNet()by passing the name of the network to it.
1 2 3 4 5 6 7 | workspace.ResetWorkspace() print("Current blobs in the workspace: {}".format(workspace.Blobs())) workspace.RunNetOnce(net) print("Blobs in the workspace after execution: {}".format(workspace.Blobs())) # Let's dump the contents of the blobs for name in workspace.Blobs(): print("{}:\n{}".format(name, workspace.FetchBlob(name))) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | Current blobs in the workspace: [] Blobs in the workspace after execution: ['W', 'X', 'Y', 'b'] W: [[-0.96537346 0.42591459 0.66788739] [-0.47695673 2.25724339 -0.10370601] [-0.20327474 -3.07469416 0.47715324] [-1.62159526 0.73711687 -1.42365313] [ 0.60718107 -0.50448036 -1.17132831]] X: [[-0.99601173 -0.61438894 0.10042733] [ 0.23359862 0.15135486 0.77555442]] Y: [[ 1.76692021 0.07781416 3.13944149 2.01927781 0.58755434] [ 1.35693741 1.14979863 0.85720366 -0.37135673 0.15705228]] b: [ 1. 1. 1. 1. 1.] |
Now let’s try the second way to create the net, and run it. First clear the variables with ResetWorkspace(), create the net with the workspace’s net object you created earlier CreateNet(net_object), and then run the net by name with RunNet(net_name).
1 2 3 4 5 6 7 | workspace.ResetWorkspace() print("Current blobs in the workspace: {}".format(workspace.Blobs())) workspace.CreateNet(net) workspace.RunNet(net.Proto().name) print("Blobs in the workspace after execution: {}".format(workspace.Blobs())) for name in workspace.Blobs(): print("{}:\n{}".format(name, workspace.FetchBlob(name))) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | Current blobs in the workspace: [] Blobs in the workspace after execution: ['W', 'X', 'Y', 'b'] W: [[-0.29295802 0.02897477 -1.25667715] [-1.82299471 0.92877913 0.33613944] [-0.64382178 -0.68545657 -0.44015241] [ 1.10232282 1.38060772 -2.29121733] [-0.55766547 1.97437167 0.39324901]] X: [[-0.47522315 -0.40166432 0.7179445 ] [-0.8363331 -0.82451206 1.54286408]] Y: [[ 0.22535783 1.73460138 1.2652775 -1.72335696 0.7543118 ] [-0.71776152 2.27745867 1.42452145 -4.59527397 0.4452306 ]] b: [ 1. 1. 1. 1. 1.] |
There are a few differences between RunNetOnce and RunNet, but probably the main difference is the computation time overhead. Since RunNetOnce involves serializing the protobuf to pass between Python and C and instantiating the network, it may take longer to run. Let’s see in this case what the overhead is.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | # It seems that %timeit magic does not work well with # C++ extensions so we'll basically do for loops start = time.time() for i in range(1000): workspace.RunNetOnce(net) end = time.time() print('Run time per RunNetOnce: {}'.format((end - start) / 1000)) start = time.time() workspace.CreateNet(net) for i in range(1000): workspace.RunNet(net.Proto().name) end = time.time() print('Run time per RunNet: {}'.format((end - start) / 1000)) |
1 2 | Run time per RunNetOnce: 0.000364284992218 Run time per RunNet: 4.42600250244e-06 |
OK, so above are a few key components if you would like to use Caffe2 from the python side. We are going to add more to the tutorial as we find more needs. For now, kindly check out the rest of the tutorials!