
 |
A subdivision method recursively refines a coarse mesh and generates an ever closer approximation to a smooth surface. Subdivision_method_3 consists of four subdivision methods and their refinement hosts. Each refinement host is a template function of a polyhedron class and a geometry policy class. It refines the connectivity of the control mesh and computes the geometry of the refined mesh. The geometry computation is dedicated to the custom geometry policy. A geometry policy consists of functions that compute the new point based on the subdivision stencil. A stencil defines the footprint (a submesh of the control mesh) of a new point.
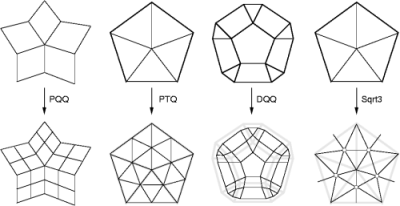
The four supported refinement hosts are the primal quadrilateral quadrisection (PQQ), the primal triangle quadrisection (PTQ), the dual quadrilateral quadrisection (DQQ), and the √3 triangulation. These refinements are respectively used in Catmull-Clark, Loop, Doo-Sabin and √3 subdivision.
#include <CGAL/Subdivision_method_3.h>
|
| ||
|
|
| |
| applies the PQQ refinement on the control mesh p step times. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. | ||
|
| ||
|
|
| |
| applies the PTQ refinement on the control mesh p step times, where p contains only triangle facets. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. The result of a non-triangle mesh p is undefined. | ||
|
| ||
|
|
| |
| applies the DQQ refinement on the control mesh p step times. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. | ||
|
| ||
|
|
| |
| applies the √3 triangulation on the control mesh p step times, where p contains only triangle facets. The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. The result of a non-triangle mesh p is undefined. | ||
|
| ||
|
|
| |
| applies Catmull-Clark subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
|
| ||
|
|
| |
| applies Loop subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
|
| ||
|
|
| |
| applies Doo-Sabin subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
|
| ||
|
|
| |
| applies √3 subdivision step times on the control mesh p. This function overwrites the control mesh p with the subdivided mesh. | ||
CGAL::CatmullClark_mask_3<Polyhedron_3>
CGAL::Loop_mask_3<Polyhedron_3>
CGAL::Sqrt3_mask_3<Polyhedron_3>
This example program subdivides a polyhedral mesh with Catmull-Clark subdivision.
File: examples/Subdivision_method_3/CatmullClark_subdivision.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Subdivision_method_3.h>
#include <iostream>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
typedef CGAL::Simple_cartesian<double> Kernel;
typedef CGAL::Polyhedron_3<Kernel> Polyhedron;
using namespace std;
using namespace CGAL;
int main(int argc, char** argv) {
if (argc != 2) {
cout << "Usage: CatmullClark_subdivision d < filename" << endl;
cout << " d: the depth of the subdivision (0 < d < 10)" << endl;
cout << " filename: the input mesh (.off)" << endl;
return 0;
}
int d = argv[1][0] - '0';
Polyhedron P;
cin >> P; // read the .off
Subdivision_method_3::CatmullClark_subdivision(P,d);
cout << P; // write the .off
return 0;
}