Advanced Search

Log In | Not a Member? Contact ADC

Remote Authentication

This is one of the more difficult problems in computer security: the ability to identify someone connecting to a computer remotely. One of the most secure methods is the use of public key cryptography, which is described in more detail in “Key-based Authentication and Encryption”. However, many other means of authentication are possible, with varying degrees of security.

Some other authentication schemes include:

• blind trust

• IP-only authentication

• password (shared secret) authentication

• combination of IP and password authentication

• one-time pads (challenge-response)

• time-based authentication

Most of these are obvious, and require no further explanation. However, one-time pads and time-based authentication may be unfamiliar to many people outside security circles, and are thus worth mentioning in more detail.

In this section:

One-Time Pads
Time-based authentication

One-Time Pads

Based on the concept of “challenge-response” pairs, one-time pad (OTP) authentication requires that both parties have an identical list of pairs of numbers, words, symbols, or whatever, sorted by the first item. When trying to access a remote system, the remote system prompts the user with a challenge. The user finds the challenge in the first column, then sends back the matching response. Alternatively, this could be an automated exchange between two pieces of software.

For maximum security, no challenge should ever be issued twice. For this reason, and because these systems were initially implemented with a paper pad containing challenge-response, or CR pairs, such systems are often called one-time pads.

The one-time nature of OTP authentication makes it impossible for someone to guess the appropriate response to any one particular challenge by a brute force attack (by responding to that challenge repeatedly with different answers). Basically, the only way to break such a system, short of a lucky guess, is to actually know some portion of the contents of the list of pairs.

For this reason, one-time pads can be used over insecure communication channels. If someone snoops the communication, they can obtain that challenge-response pair. However, that information is of no use to them, since that particular challenge will never be issued again. (It does not even reduce the potential sample space for responses, since only the challenges must be unique.)

Time-based authentication

This is probably the least understood means of authentication, though it is commonly used by such technologies as SecurID. The concept is relatively straightforward. You begin with a mathematical function that takes a small number of parameters (two, for example) and returns a new parameter. A good example of such a function is the function that generates the set of Fibonacci numbers (possibly truncated after a certain number of bits, with arbitrary initial seed values).

Take this function, and add a third parameter, t, representing time in units of k seconds. Make the function be a generating function on t, with two seed values, a and b, where

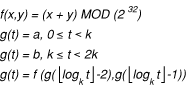
In other words, every k seconds, you calculate a new value based on the previous two and some equation. Then discard the oldest value, replacing it with the second oldest value, and replace the second oldest value with the value that you just generated.

As long as both ends have the same notion of the current time and the original two numbers, they can then calculate the most recently generated number and use this as a shared secret. Of course, if you are writing code that does this, you should use a closed form of this equation, since calculating Fibonacci numbers recursively without additional storage grows at O(2^(t/k)), which is not practical when t is measured in years and k is a small constant measured in seconds.

The security of such a scheme depends on various properties of the generator function, and the details of such a function are beyond the scope of this document. For more information, you should obtain an introductory text on cryptography,. such as Bruce Schneier’s Applied Cryptography.

Did this document help you? Yes: Tell us what works for you. It’s good, but: Report typos, inaccuracies, and so forth. It wasn’t helpful: Tell us what would have helped.

	Get information on Apple products. Visit the Apple Store online or at retail locations. 1-800-MY-APPLE Copyright © 2007 Apple Inc. All rights reserved. | Terms of use | Privacy Notice