This module provides generic bounding volume hierarchy algorithms and reference tree implementations.
* #include <unsupported/Eigen/BVH>
*
A bounding volume hierarchy (BVH) can accelerate many geometric queries. This module provides a generic implementation of the two basic algorithms over a BVH: intersection of a query object against all objects in the hierarchy and minimization of a function over the objects in the hierarchy. It also provides intersection and minimization over a cartesian product of two BVH's. A BVH accelerates intersection by using the fact that if a query object does not intersect a volume, then it cannot intersect any object contained in that volume. Similarly, a BVH accelerates minimization because the minimum of a function over a volume is no greater than the minimum of a function over any object contained in it.
Some sample queries that can be written in terms of intersection are:
- Determine all points where a ray intersects a triangle mesh
- Given a set of points, determine which are contained in a query sphere
- Given a set of spheres, determine which contain the query point
- Given a set of disks, determine if any is completely contained in a query rectangle (represent each 2D disk as a point
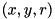 in 3D and represent the rectangle as a pyramid based on the original rectangle and shrinking in the
in 3D and represent the rectangle as a pyramid based on the original rectangle and shrinking in the 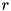 direction)
direction)
- Given a set of points, count how many pairs are
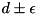 apart (done by looking at the cartesian product of the set of points with itself)
apart (done by looking at the cartesian product of the set of points with itself)
Some sample queries that can be written in terms of function minimization over a set of objects are:
- Find the intersection between a ray and a triangle mesh closest to the ray origin (function is infinite off the ray)
- Given a polyline and a query point, determine the closest point on the polyline to the query
- Find the diameter of a point cloud (done by looking at the cartesian product and using negative distance as the function)
- Determine how far two meshes are from colliding (this is also a cartesian product query)
This implementation decouples the basic algorithms both from the type of hierarchy (and the types of the bounding volumes) and from the particulars of the query. To enable abstraction from the BVH, the BVH is required to implement a generic mechanism for traversal. To abstract from the query, the query is responsible for keeping track of results.
To be used in the algorithms, a hierarchy must implement the following traversal mechanism (see KdBVH for a sample implementation):
typedef Volume
typedef Object
typedef Index
typedef VolumeIterator
typedef ObjectIterator
Index getRootIndex() const
const Volume &getVolume(Index index) const
void getChildren(Index index, VolumeIterator &outVBegin, VolumeIterator &outVEnd,
ObjectIterator &outOBegin, ObjectIterator &outOEnd) const
To use the hierarchy, call BVIntersect or BVMinimize, passing it a BVH (or two, for cartesian product) and a minimizer or intersector. For an intersection query on a single BVH, the intersector encapsulates the query and must provide two functions:
bool intersectVolume(const Volume &volume)
bool intersectObject(const Object &object)
The guarantee that BVIntersect provides is that intersectObject will be called on every object whose bounding volume intersects the query (but possibly on other objects too) unless the search is terminated prematurely. It is the responsibility of the intersectObject function to keep track of the results in whatever manner is appropriate. The cartesian product intersection and the BVMinimize queries are similar–see their individual documentation.
The following is a simple but complete example for how to use the BVH to accelerate the search for a closest red-blue point pair:
#include <Eigen/StdVector>
#include <unsupported/Eigen/BVH>
#include <iostream>
using namespace Eigen;
typedef AlignedBox<double, 2> Box2d;
namespace Eigen {
namespace internal {
Box2d bounding_box(const Vector2d &v) { return Box2d(v, v); }
}
}
struct PointPointMinimizer
{
PointPointMinimizer() : calls(0) {}
typedef double Scalar;
double minimumOnVolumeVolume(const Box2d &r1, const Box2d &r2) { ++calls; return r1.squaredExteriorDistance(r2); }
double minimumOnVolumeObject(const Box2d &r, const Vector2d &v) { ++calls; return r.squaredExteriorDistance(v); }
double minimumOnObjectVolume(const Vector2d &v, const Box2d &r) { ++calls; return r.squaredExteriorDistance(v); }
double minimumOnObjectObject(const Vector2d &v1, const Vector2d &v2) { ++calls; return (v1 - v2).squaredNorm(); }
int calls;
};
int main()
{
typedef std::vector<Vector2d, aligned_allocator<Vector2d> > StdVectorOfVector2d;
StdVectorOfVector2d redPoints, bluePoints;
for(int i = 0; i < 100; ++i) {
redPoints.push_back(Vector2d::Random());
bluePoints.push_back(Vector2d::Random());
}
PointPointMinimizer minimizer;
double minDistSq = std::numeric_limits<double>::max();
for(int i = 0; i < (int)redPoints.size(); ++i)
for(int j = 0; j < (int)bluePoints.size(); ++j)
minDistSq = std::min(minDistSq, minimizer.minimumOnObjectObject(redPoints[i], bluePoints[j]));
std::cout << "Brute force distance = " << sqrt(minDistSq) << ", calls = " << minimizer.calls << std::endl;
minimizer.calls = 0;
minDistSq =
BVMinimize(redTree, blueTree, minimizer);
std::cout << "BVH distance = " << sqrt(minDistSq) << ", calls = " << minimizer.calls << std::endl;
return 0;
}
Output:
Brute force distance = 0.00428018, calls = 10000
BVH distance = 0.00428018, calls = 756


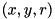 in 3D and represent the rectangle as a pyramid based on the original rectangle and shrinking in the
in 3D and represent the rectangle as a pyramid based on the original rectangle and shrinking in the 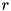 direction)
direction)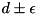 apart (done by looking at the cartesian product of the set of points with itself)
apart (done by looking at the cartesian product of the set of points with itself)