 |
Eigen-unsupported
3.2.7
|
 |
Eigen-unsupported
3.2.7
|
This module provides a QR based polynomial solver.
To use this module, add
at the start of your source file.
Classes | |
| class | PolynomialSolver< _Scalar, _Deg > |
| A polynomial solver. More... | |
| class | PolynomialSolverBase< _Scalar, _Deg > |
| Defined to be inherited by polynomial solvers: it provides convenient methods such as. More... | |
Functions | |
| template<typename Polynomial > | |
| NumTraits< typename Polynomial::Scalar >::Real | cauchy_max_bound (const Polynomial &poly) |
| template<typename Polynomial > | |
| NumTraits< typename Polynomial::Scalar >::Real | cauchy_min_bound (const Polynomial &poly) |
| template<typename Polynomials , typename T > | |
| T | poly_eval (const Polynomials &poly, const T &x) |
| template<typename Polynomials , typename T > | |
| T | poly_eval_horner (const Polynomials &poly, const T &x) |
| template<typename RootVector , typename Polynomial > | |
| void | roots_to_monicPolynomial (const RootVector &rv, Polynomial &poly) |
and a QR based polynomial solver. The remainder of the page documents first the functions for evaluating, computing polynomials, computing estimates about polynomials and next the QR based polynomial solver.
The function
computes the coefficients 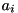 of
of
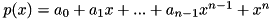
where \form#39 is known through its roots i.e. \form#40.
The function
evaluates a polynomial at a given point using stabilized Hörner method.
The following code: first computes the coefficients in the monomial basis of the monic polynomial that has the provided roots; then, it evaluates the computed polynomial, using a stabilized Hörner method.
Output:
Roots: 0.680375 -0.211234 0.566198 0.59688 Polynomial: -0.04857.x^0+ 0.00860842.x^1+ 0.739882.x^2+ -1.63222.x^3+ 1.x^4 Evaluation of the polynomial at the roots: -2.08167e-17 0 0 2.08167e-17
The function
provides a maximum bound (the Cauchy one: 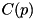 ) for the absolute value of a root of the given polynomial i.e.
) for the absolute value of a root of the given polynomial i.e. 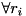 root of
root of 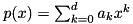 ,
, 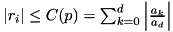 The leading coefficient
The leading coefficient  : should be non zero
: should be non zero  .
.
The function
provides a minimum bound (the Cauchy one: 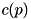 ) for the absolute value of a non zero root of the given polynomial i.e.
) for the absolute value of a non zero root of the given polynomial i.e. 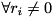 root of
root of 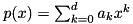 ,
, 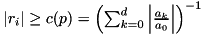
Computes the complex roots of a polynomial by computing the eigenvalues of the associated companion matrix with the QR algorithm.
The roots of 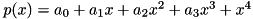 are the eigenvalues of
are the eigenvalues of ![$ \left [ \begin{array}{cccc} 0 & 0 & 0 & a_0 \\ 1 & 0 & 0 & a_1 \\ 0 & 1 & 0 & a_2 \\ 0 & 0 & 1 & a_3 \end{array} \right ] $](form_50.png)
However, the QR algorithm is not guaranteed to converge when there are several eigenvalues with same modulus. Therefore the current polynomial solver is guaranteed to provide a correct result only when the complex roots \form#51 have distinct moduli i.e.
![$ \forall i,j \in [1;d],~ \| r_i \| \neq \| r_j \| $](form_52.png) .
.
With 32bit (float) floating types this problem shows up frequently.
However, almost always, correct accuracy is reached even in these cases for 64bit (double) floating types and small polynomial degree (<20).
\include PolynomialSolver1.cpp In the above example: -# a simple use of the polynomial solver is shown; -# the accuracy problem with the QR algorithm is presented: a polynomial with almost conjugate roots is provided to the solver. Those roots have almost same module therefore the QR algorithm failed to converge: the accuracy of the last root is bad; -# a simple way to circumvent the problem is shown: use doubles instead of floats.
Output:
Roots: 0.680375 -0.211234 0.566198 0.59688 0.823295 Complex roots: (-0.211234,0) (0.566198,0) (0.59688,0) (0.680375,0) (0.823295,0) Real roots: -0.211234 0.566198 0.59688 0.680375 0.823295 Illustration of the convergence problem with the QR algorithm: --------------------------------------------------------------- Hard case polynomial defined by floats: -0.957 0.9219 0.3516 0.9453 -0.4023 -0.5508 -0.03125 Complex roots: (1.19707,0) (0.70514,0) (-1.9834,0) (-0.396563,0.966801) (-0.396563,-0.966801) (-16.7513,0) Norms of the evaluations of the polynomial at the roots: 3.72694e-07 1.43051e-06 1.76896e-05 1.74676e-06 1.74676e-06 0.0823092 Using double's almost always solves the problem for small degrees: ------------------------------------------------------------------- Complex roots: (1.19707,0) (0.70514,0) (-1.9834,0) (-0.396564,0.966801) (-0.396564,-0.966801) (-16.7513,0) Norms of the evaluations of the polynomial at the roots: 3.78175e-07 0 2.0411e-06 2.48518e-07 2.48518e-07 0 The last root in float then in double: (-16.75127983,0) (-16.75128099,0) Norm of the difference: 1.907348633e-06
|
inline |
| [in] | poly | : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 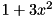 is stored as a vector is stored as a vector ![$ [ 1, 0, 3 ] $](form_76.png) . . |
Precondition: the leading coefficient of the input polynomial poly must be non zero
|
inline |
| [in] | poly | : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 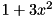 is stored as a vector is stored as a vector ![$ [ 1, 0, 3 ] $](form_76.png) . . |
|
inline |
| [in] | poly | : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 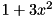 is stored as a vector is stored as a vector ![$ [ 1, 0, 3 ] $](form_76.png) . . |
| [in] | x | : the value to evaluate the polynomial at. |
References Eigen::poly_eval_horner().
|
inline |
| [in] | poly | : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 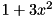 is stored as a vector is stored as a vector ![$ [ 1, 0, 3 ] $](form_76.png) . . |
| [in] | x | : the value to evaluate the polynomial at. |
Note for stability: 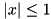
Referenced by Eigen::poly_eval().
| void Eigen::roots_to_monicPolynomial | ( | const RootVector & | rv, |
| Polynomial & | poly | ||
| ) |
Given the roots of a polynomial compute the coefficients in the monomial basis of the monic polynomial with same roots and minimal degree. If RootVector is a vector of complexes, Polynomial should also be a vector of complexes.
| [in] | rv | : a vector containing the roots of a polynomial. |
| [out] | poly | : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 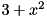 is stored as a vector is stored as a vector ![$ [ 3, 0, 1 ] $](form_79.png) . . |