 ; all other line segments are y-major
(slope is determined by the segment's endpoints).
We shall specify rasterization only for x-major segments except in
cases where the modifications for y-major segments are not self-evident.
; all other line segments are y-major
(slope is determined by the segment's endpoints).
We shall specify rasterization only for x-major segments except in
cases where the modifications for y-major segments are not self-evident.
Line segment rasterization begins by characterizing the segment as either
x-major or y-major.
x-major line segments have slope in the closed
interval  ; all other line segments are y-major
(slope is determined by the segment's endpoints).
We shall specify rasterization only for x-major segments except in
cases where the modifications for y-major segments are not self-evident.
; all other line segments are y-major
(slope is determined by the segment's endpoints).
We shall specify rasterization only for x-major segments except in
cases where the modifications for y-major segments are not self-evident.
Ideally, the GL uses a ``diamond-exit'' rule to determine those fragments
that are produced by rasterizing a line segment. For each fragment f
with center at window coordinates 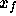 and
and 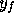 , define a diamond-shaped
region that is the intersection of four half planes:
, define a diamond-shaped
region that is the intersection of four half planes:
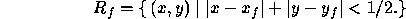
Essentially, a line segment starting at 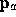 and ending at
and ending at 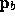 produces those fragments f for which the segment intersects
produces those fragments f for which the segment intersects 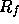 ,
except if
,
except if  is contained in
is contained in 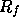 .
See Figure 3.4.
.
See Figure 3.4.
To avoid difficulties when an endpoint lies on a boundary of 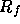 we (in principle) perturb the supplied endpoints by a tiny amount.
Let
we (in principle) perturb the supplied endpoints by a tiny amount.
Let  and
and 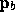 have window coordinates
have window coordinates 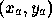 and
and
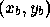 , respectively.
Obtain the perturbed endpoints
, respectively.
Obtain the perturbed endpoints 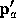 given by
given by
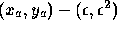 and
and 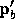 given by
given by
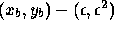 .
Rasterizing the line segment starting at
.
Rasterizing the line segment starting at
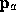 and ending at
and ending at 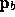 produces those fragments f
for which the segment starting at
produces those fragments f
for which the segment starting at 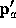 and ending on
and ending on
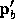 intersects
intersects 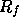 , except if
, except if 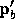 is contained in
is contained in 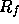 .
.
 is chosen to be so small that rasterizing the line
segment produces the same fragments when
is chosen to be so small that rasterizing the line
segment produces the same fragments when  is substituted
for
is substituted
for  for any
for any 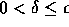 .
.
When  and
and  lie on fragment centers,
this characterization of fragments reduces to Bresenham's algorithm
with one modification:
lines produced in this description are
``half-open,'' meaning that the final fragment (corresponding to
lie on fragment centers,
this characterization of fragments reduces to Bresenham's algorithm
with one modification:
lines produced in this description are
``half-open,'' meaning that the final fragment (corresponding to
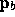 ) is not drawn.
This means that when rasterizing a series of connected line segments,
shared endpoints will be produced only once rather than twice (as would occur
with Bresenham's algorithm).
) is not drawn.
This means that when rasterizing a series of connected line segments,
shared endpoints will be produced only once rather than twice (as would occur
with Bresenham's algorithm).

Figure 3.4: Visualization of Bresenham's algorithm.
A portion of a line segment is shown.
A diamond shaped region of height 1 is placed around each fragment center;
those regions that the line segment exits cause rasterization to produce
corresponding fragments.
Because the initial and final conditions of the diamond-exit rule may be difficult to implement, other line segment rasterization algorithms are allowed, subject to the following rules:
Next we must specify how the data associated with each rasterized fragment
are obtained.
Let the window coordinates of a produced fragment center be given by
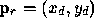 and let
and let 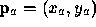 and
and  .
Set
.
Set
(Note that t=0 at  and t=1 at
and t=1 at 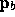 .)
The value of an associated datum f for the fragment,
whether it be R, G, B, or A (in RGBA mode) or a color index
(in color index mode), or the s, t, or r texture coordinate
(the depth value, window z, must be found using equation 3.3,
below),
is found as
.)
The value of an associated datum f for the fragment,
whether it be R, G, B, or A (in RGBA mode) or a color index
(in color index mode), or the s, t, or r texture coordinate
(the depth value, window z, must be found using equation 3.3,
below),
is found as
where 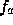 and
and 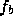 are the data associated with the starting and ending
endpoints of the segment, respectively;
are the data associated with the starting and ending
endpoints of the segment, respectively;
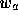 and
and 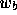 are the clip w coordinates of the starting and ending
endpoints of the segments, respectively.
are the clip w coordinates of the starting and ending
endpoints of the segments, respectively.
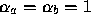 for all data except texture coordinates,
in which case
for all data except texture coordinates,
in which case 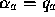 and
and  (
(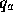 and
and 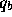 are
the homogeneous texture coordinates at the starting and ending endpoints
of the segment; results are undefined if either of these is less than
or equal to 0).
Note that linear interpolation would use
are
the homogeneous texture coordinates at the starting and ending endpoints
of the segment; results are undefined if either of these is less than
or equal to 0).
Note that linear interpolation would use
The reason that this formula is incorrect (except for the depth value) is that it interpolates a datum in window space, which may be distorted by perspective. What is actually desired is to find the corresponding value when interpolated in eye space, which equation 3.2 does. A GL implementation may choose to approximate equation 3.2 with 3.3, but this will normally lead to unacceptable distortion effects when interpolating texture coordinates.