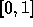 ,
with a+b+c = 1.
These coordinates uniquely specify any point p within the triangle or on
the triangle's boundary as
,
with a+b+c = 1.
These coordinates uniquely specify any point p within the triangle or on
the triangle's boundary as
The first step of polygon rasterization is to determine if the polygon is back facing or front facing. This determination is made by examining the sign of the area computed by equation 2.6 of section 2.13.1 (including the possible reversal of this sign as indicated by the last call to FrontFace ). If this sign is positive, the polygon is frontfacing; otherwise, it is back facing. This determination is used in conjunction with the CullFace enable bit and mode value to decide whether or not a particular polygon is rasterized. The CullFace mode is set by calling
mode is a symbolic constant: one of FRONT, BACK or FRONT_AND_BACK. Culling is enabled or disabled with Enable or Disable using the symbolic constant CULL_FACE. Front facing polygons are rasterized if either culling is disabled or the CullFace mode is BACK while back facing polygons are rasterized only if either culling is disabled or the CullFace mode is FRONT. The initial setting of the CullFace mode is BACK. Initially, culling is disabled.
The rule for determining which fragments are produced by polygon rasterization is called point sampling. The two-dimensional projection obtained by taking the x and y window coordinates of the polygon's vertices is formed. Fragment centers that lie inside of this polygon are produced by rasterization. Special treatment is given to a fragment whose center lies on a polygon boundary edge. In such a case we require that if two polygons lie on either side of a common edge (with identical endpoints) on which a fragment center lies, then exactly one of the polygons results in the production of the fragment during rasterization.
As for the data associated with each fragment produced
by rasterizing a polygon,
we begin by specifying how these
values are produced for fragments in a triangle.
Define barycentric coordinates for a triangle.
Barycentric coordinates are a set of three numbers,
a, b, and c, each in the range 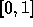 ,
with a+b+c = 1.
These coordinates uniquely specify any point p within the triangle or on
the triangle's boundary as
,
with a+b+c = 1.
These coordinates uniquely specify any point p within the triangle or on
the triangle's boundary as

where 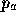 ,
, 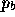 , and
, and 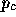 are the vertices of the triangle.
a, b, and c can be found as
are the vertices of the triangle.
a, b, and c can be found as
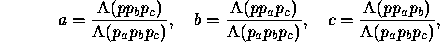
where 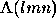 denotes the area in window coordinates
of the triangle with vertices l, m, and n.
denotes the area in window coordinates
of the triangle with vertices l, m, and n.
Denote a datum at 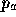 ,
, 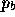 , or
, or 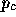 as
as 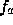 ,
, 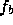 , or
, or 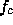 ,
respectively.
Then the value f of a datum at a fragment produced by rasterizing a triangle
is given by
,
respectively.
Then the value f of a datum at a fragment produced by rasterizing a triangle
is given by
where 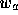 ,
, 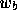 and
and 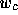 are the clip w coordinates of
are the clip w coordinates of 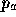 ,
, 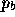 ,
and
,
and 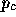 , respectively.
a, b, and c are the barycentric coordinates of the fragment for which
the data are produced.
, respectively.
a, b, and c are the barycentric coordinates of the fragment for which
the data are produced.
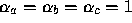 except for texture s, t, and r
coordinates,
for which
except for texture s, t, and r
coordinates,
for which 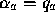 ,
, 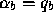 , and
, and 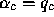 (if any of
(if any of 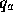 ,
, 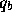 , or
, or 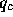 are less than or equal to zero,
results are undefined).
a, b, and c must correspond precisely
to the exact coordinates of the center of the fragment.
Another way of saying this is that the data associated with a fragment
must be sampled at the fragment's center.
are less than or equal to zero,
results are undefined).
a, b, and c must correspond precisely
to the exact coordinates of the center of the fragment.
Another way of saying this is that the data associated with a fragment
must be sampled at the fragment's center.
Just as with line segment rasterization, equation 3.4 may be approximated by
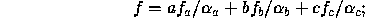
this may yield acceptable results for color values (it must be used for depth values), but will normally lead to unacceptable distortion effects if used for texture coordinates.
For a polygon with more than three edges, we require only that a convex combination of the values of the datum at the polygon's vertices can be used to obtain the value assigned to each fragment produced by the rasterization algorithm. That is, it must be the case that at every fragment

where n is the number of vertices in the polygon,
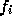 is the value of the f at vertex i;
for each i
is the value of the f at vertex i;
for each i 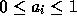 and
and 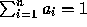 .
The values of the
.
The values of the 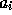 may differ
from fragment to fragment,
but at vertex i,
may differ
from fragment to fragment,
but at vertex i,
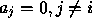 and
and 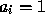 .
.
One algorithm that achieves the required behavior is to triangulate a polygon (without adding any vertices) and then treat each triangle individually as already discussed. A scan-line rasterizer that linearly interpolates data along each edge and then linearly interpolates data across each horizontal span from edge to edge also satisfies the restrictions (in this case, the numerator and denominator of equation 3.4 should be iterated independently and a division performed for each fragment).