[email protected]
Artelnics - Making intelligent use of data
In this tutorial we formulate the learning problem for neural networks and describe some learning tasks that they can solve.
Contents:The objective is the most important term in the performance functional expression. It defines the task that the neural network is required to accomplish.
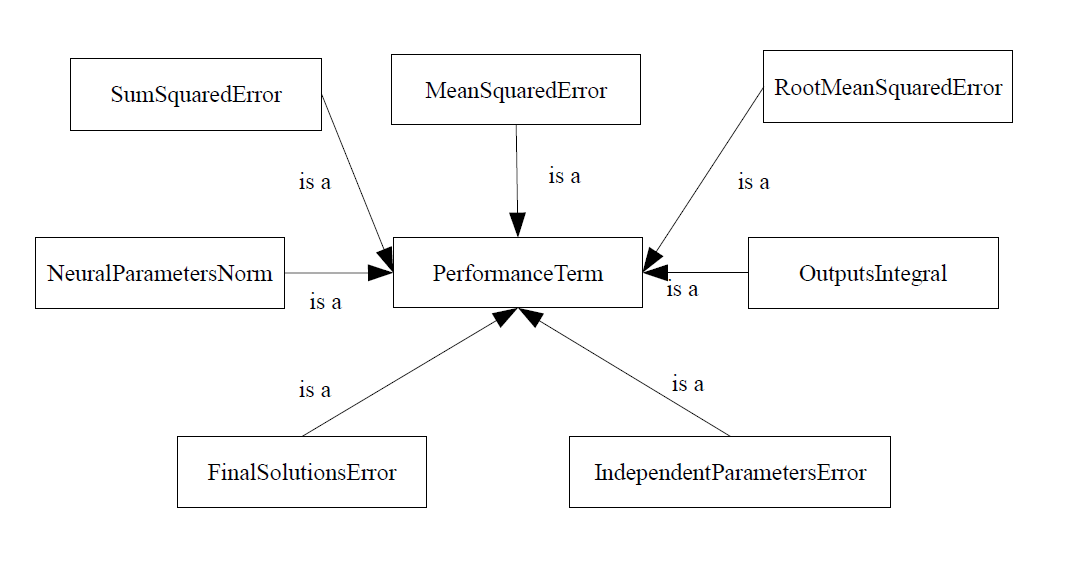
For data modeling applications, such as function regression or pattern recognition, the sum squared error is the reference objective functional. It measures the difference between the outputs from a neural network and the targets in a data set. Some related objective functionals here are the normalized squared error or the Minkowski error.
Applications in which the neural network learns from a mathematical model require other objective functionals. For instance, we can talk about minimum final time or desired trajectory optimal control problems. That two performance terms are called in OpenNN independent parameters error and solutions error, respectively.
A problem is called well-posed if its solution meets existence, uniqueness and stability. A solution is said to be stable when small changes in the independent variable led to small changes in the dependent variable. Otherwise the problem is said to be ill-posed.
An approach for ill-posed problems is to control the effective complexity of the neural network. This can be achieved by using a regularization term into the performance functional.
One of the simplest forms of regularization term consists on the norm of the neural parameters vector. Adding that term to the objective functional will cause the neural network to have smaller weights and biases, and this will force its response to be smoother.
Regularization can be used in problems which learn from a data set. Function regression or pattern recognition problems with noisy data sets are common applications. It is also useful in optimal control problems which aim to save control action.
A variational problem for a neural network can be specified by a set of constraints, which are equalities or inequalities that the solution must satisfy. Such constraints are expressed as functionals.
Here the aim is to find a solution which makes all the constraints to be satisfied and the objective functional to be an extremum.
Constraints are required in many optimal control or optimal shape design problems. For instance, we can talk about length, area or volume constraints.
The performance measure is a functional of the neural network which can take the following forms:
performance functional = Functional[neural network] performance functional = Functional[neural network, data set] performance functional = Functional[neural network, mathematical model] performance functional = Functional[neural network, mathematical model, data set]
In order to perform a particular task a neural network must be associated a performance functional, which depends on the variational problem at hand. The learning problem is thus formulated in terms of the minimization of the performance functional.
The performance functional defines the task that the neural network is required to accomplish and provides a measure of the quality of the representation that the neural network is required to learn. In this way, the choice of a suitable performance functional depends on the particular application.
The learning problem can then be stated as to find a neural network for which the performance functional takes on a minimum or a maximum value. This is a variational problem.
In the context of neural network, the variational problems are can be treated as a function optimization problem. The variational approach looks at the performance as being a functional of the function represented by the neural network. The optimization approach looks at the performance as being a function of the parameters in the neural network.
Then, a performance function can be visualized as a hypersurface, with the neural network parameters as coordinates, the following figure represents the performance function.The performance function evaluates the performance of the neural network by looking at its parameters. More complex calculations allow to obtain some partial derivatives of the performance with respect to the parameters. The first partial derivatives are arranged in the gradient vector. The second partial derivatives are arranged in the Hessian matrix.
When the desired output of the neural network for a given input is known, the gradient and Hessian can usually be found analytically using back-propagation. In some other circumstances exact evaluation of that quantities is not possible and numerical differentiation must be used.
performance functional = objective term + regularization term + constraints term
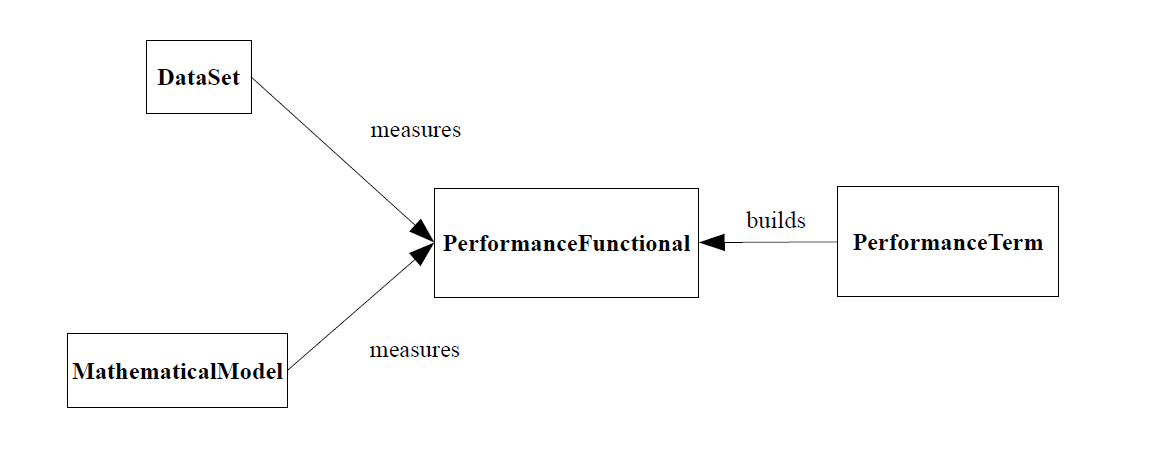
OpenNN implements the PerformanceFunctional concrete class. This class manages different objective, regularization and constraints terms in order to construct a performance functional suitable for our problem.
All that members are declared as private, and they can only be used with their corresponding get or set methods.
As it has been said, the choice of the performance functional depends on the particular application. A default performance functional is not associated to a neural network, it is not measured on a data set or a mathematical model,
PerformanceFunctional pf;
The default objective functional in the performance functional above is a normalized squared error. This is very used in function regression, pattern recognition and time series prediction.
That performance functional does not contain any regularization or constraints terms by default. Also, it does not have numerical differentiation utilities.
The following sentence constructs a performance functional associated to a neural network and to be measured on a data set.
NeuralNetwork nn(1, 1); DataSet ds(1, 1, 1); ds.initialize_data(0.0); PerformanceFunctional pf(&nn, &ds);
As before the default objective functional is the normalized squared error.
The calculate_performance method calculates the performance of some neural network. It is called as follows,
double performance = pf.calculate_performance();
Note that the evaluation of the performance functional is the sum of the objective, regularization and constraints terms.
The calculate_gradient method calculates the partial derivatives of the performance with respect to the neural network parameters.
PerformanceFunctional pf; Vector<double> gradient = pf.calculate_gradient();
As before, the gradient of the performance functional is the sum of the objective, the regularization and the constraints gradients. Most of the times, an analytical solution for the gradient is achieved. An example is the normalized squared error. On the other hand, some applications might need numerical differentiation. An example is the outputs integrals performance term.
Similarly, the Hessian matrix can be computed using the calculate_Hessian method,
Matrix<double> Hessian = pf.calculate_Hessian();
The Hessian of the objective functional is also the sum of the objective, regularization and constraints matrices of second derivatives.
If the user wants another objective functional than the default, he can writte
pf.construct_objective_term('MEAN_SQUARED_ERROR');
The above sets the objective functional to be the mean squared error.
The performance functional is not regularized by default. To change that, the following can be used
pf.construct_regularization_term('NEURAL_PARAMETERS_NORM');
The above sets the default regularization method to be the multilayer perceptron parameters norm. Also, it sets the weight for that regularization term.
Finally, the performance functional does not include a constraints term by default. The use of constrains might be difficult, so the interested reader is referred to look at the examples included in OpenNN.
OpenNN Copyright © 2014 Roberto Lopez (Artelnics)