| Description: Define the Moore
closure of a generating set, which is the smallest
closed set containing all generating elements. Definition of Moore
closure in [Schechter] p. 79. This
generalizes topological closure
(mrccls 20883) and linear span (mrclsp 18989).
A Moore closure operation  is (1) extensive, i.e., is (1) extensive, i.e.,
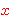 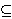 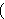   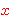 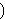 for all subsets for all subsets 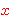 of the base set (mrcssid 16277),
(2) isotone, i.e., of the base set (mrcssid 16277),
(2) isotone, i.e., 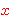 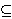
 implies that implies that 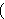   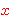 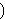 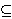 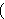    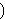 for all subsets
for all subsets 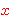 and
and  of the base set (mrcss 16276), and (3)
idempotent, i.e., of the base set (mrcss 16276), and (3)
idempotent, i.e., 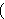   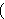      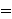 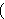   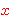 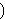 for all subsets for all subsets
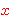 of the base set
(mrcidm 16279.) Operators satisfying these three
properties are in bijective correspondence with Moore collections, so
these properties may be used to give an alternate characterization of a
Moore collection by providing a closure operation of the base set
(mrcidm 16279.) Operators satisfying these three
properties are in bijective correspondence with Moore collections, so
these properties may be used to give an alternate characterization of a
Moore collection by providing a closure operation  on the set of
subsets of a given base set which satisfies (1), (2), and (3); the
closed sets can be recovered as those sets which equal their closures
(Section 4.5 in [Schechter] p. 82.)
(Contributed by Stefan O'Rear,
31-Jan-2015.) (Revised by David Moews,
1-May-2017.) on the set of
subsets of a given base set which satisfies (1), (2), and (3); the
closed sets can be recovered as those sets which equal their closures
(Section 4.5 in [Schechter] p. 82.)
(Contributed by Stefan O'Rear,
31-Jan-2015.) (Revised by David Moews,
1-May-2017.) |