Definition df-oc 28109

Description: Define orthogonal complement of a subset (usually a subspace) of Hilbert space. The orthogonal complement is the set of all vectors orthogonal to all vectors in the subset. See ocval 28139 and chocvali 28158 for its value. Textbooks usually denote this unary operation with the symbol 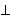_|_ as a small superscript, although Mittelstaedt uses the symbol as a prefix operation. Here we define a function (prefix operation) 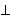_|_ rather than introducing a new syntactic form. This lets us take advantage of the theorems about functions that we already have proved under set theory. Definition of [Mittelstaedt] p. 9. (Contributed by NM, 7-Aug-2000.) (New usage is discouraged.)

Assertion

Ref	Expression
df-oc	|- _|_ = ( x e. ~P ~H |-> { y e. ~H | A. z e. x ( y .ih z ) = 0 } )

Distinct variable group:   x, y, z

Detailed syntax breakdown of Definition df-oc

Step	Hyp	Ref	Expression
1		cort 27787	. 2 class _|_
2		vx	. . 3 setvar x
3		chil 27776	. . . 4 class ~H
4	3	cpw 4158	. . 3 class ~P ~H
5		vy	. . . . . . . 8 setvar y
6	5	cv 1482	. . . . . . 7 class y
7		vz	. . . . . . . 8 setvar z
8	7	cv 1482	. . . . . . 7 class z
9		csp 27779	. . . . . . 7 class .ih
10	6, 8, 9	co 6650	. . . . . 6 class ( y .ih z )
11		cc0 9936	. . . . . 6 class 0
12	10, 11	wceq 1483	. . . . 5 wff ( y .ih z ) = 0
13	2	cv 1482	. . . . 5 class x
14	12, 7, 13	wral 2912	. . . 4 wff A. z e. x ( y .ih z ) = 0
15	14, 5, 3	crab 2916	. . 3 class { y e. ~H | A. z e. x ( y .ih z ) = 0 }
16	2, 4, 15	cmpt 4729	. 2 class ( x e. ~P ~H |-> { y e. ~H | A. z e. x ( y .ih z ) = 0 } )
17	1, 16	wceq 1483	1 wff _|_ = ( x e. ~P ~H |-> { y e. ~H | A. z e. x ( y .ih z ) = 0 } )

This definition is referenced by:  ocval  28139