Description: Define the class of
planar incidence geometries. We use Hilbert's
axioms and adapt them to planar geometry. We use  for the
incidence relation. We could have used a generic binary relation, but
using for the
incidence relation. We could have used a generic binary relation, but
using  allows
us to reuse previous results. Much of what follows
is directly borrowed from Aitken, Incidence-Betweenness Geometry,
2008, http://public.csusm.edu/aitken_html/m410/betweenness.08.pdf. allows
us to reuse previous results. Much of what follows
is directly borrowed from Aitken, Incidence-Betweenness Geometry,
2008, http://public.csusm.edu/aitken_html/m410/betweenness.08.pdf.
The class 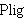 is the class of planar incidence geometries, where a
planar incidence geometry is defined as a set of lines satisfying three
axioms. In the definition below, is the class of planar incidence geometries, where a
planar incidence geometry is defined as a set of lines satisfying three
axioms. In the definition below,  denotes a planar incidence
geometry, so denotes a planar incidence
geometry, so   denotes the
union of its lines, that is, the set
of points in the plane, denotes the
union of its lines, that is, the set
of points in the plane, 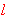 denotes a line, and denotes a line, and      denote
points. Therefore, the axioms are: 1) for all pairs of (distinct)
points, there exists a unique line containing them; 2) all lines contain
at least two points; 3) there exist three non-collinear points.
(Contributed by FL, 2-Aug-2009.) denote
points. Therefore, the axioms are: 1) for all pairs of (distinct)
points, there exists a unique line containing them; 2) all lines contain
at least two points; 3) there exist three non-collinear points.
(Contributed by FL, 2-Aug-2009.) |