Sage en quelques mots¶
Cette courte présentation de Sage reprend le “Tour of Mathematica” proposé au début du “Mathematica Book”.
La calculatrice Sage¶
La ligne de commande Sage débute par sage:. Il ne vous est pas
nécessaire de l’écrire à chaque ligne. Si vous utilisez le Notebook
de Sage, vous n’avez qu’à recopier ce qui suit sage: dans une
cellule, et à appuyer simultanément sur Maj + Entrée pour calculer
le résultat.
sage: 3 + 5
8
Comme partout, l’accent circonflexe signifie “élever à la puissance”.
sage: 57.1 ^ 100
4.60904368661396e175
Il permet de calculer des puissances d’objets plus complexes comme des matrices. Voici comment calculer l’inverse d’une matrice \(2 \times 2\) avec Sage.
sage: matrix([[1,2], [3,4]])^(-1)
[ -2 1]
[ 3/2 -1/2]
Voici comment intégrer une fonction simple.
sage: x = var('x') # Créer une variable symbolique
sage: integrate(sqrt(x)*sqrt(1+x), x)
1/4*((x + 1)^(3/2)/x^(3/2) + sqrt(x + 1)/sqrt(x))/((x + 1)^2/x^2 - 2*(x + 1)/x + 1) - 1/8*log(sqrt(x + 1)/sqrt(x) + 1) + 1/8*log(sqrt(x + 1)/sqrt(x) - 1)
Les commandes suivantes permettent de demander à Sage de résoudre une équation
quadratique. Le symbole == représente l’égalité sous Sage.
sage: a = var('a')
sage: S = solve(x^2 + x == a, x); S
[x == -1/2*sqrt(4*a + 1) - 1/2, x == 1/2*sqrt(4*a + 1) - 1/2]
Le résultat est une liste d’inégalités.
sage: S[0].rhs()
-1/2*sqrt(4*a + 1) - 1/2
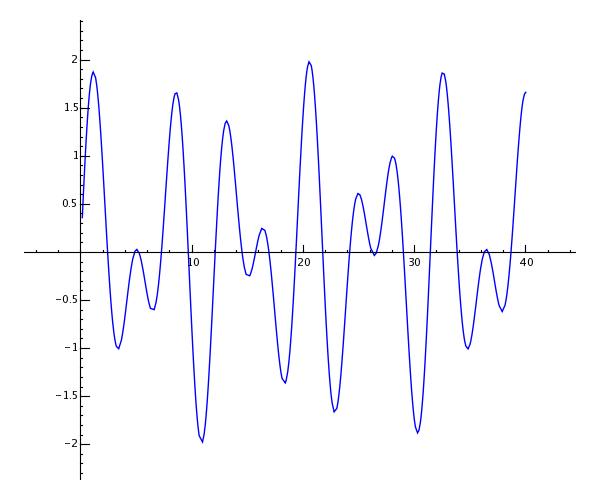
sage: show(plot(sin(x) + sin(1.6*x), 0, 40))
Calcul numérique sous Sage¶
Tout d’abord, créons une matrice aléatoire de taille \(500 \times 500\).
sage: m = random_matrix(RDF,500)
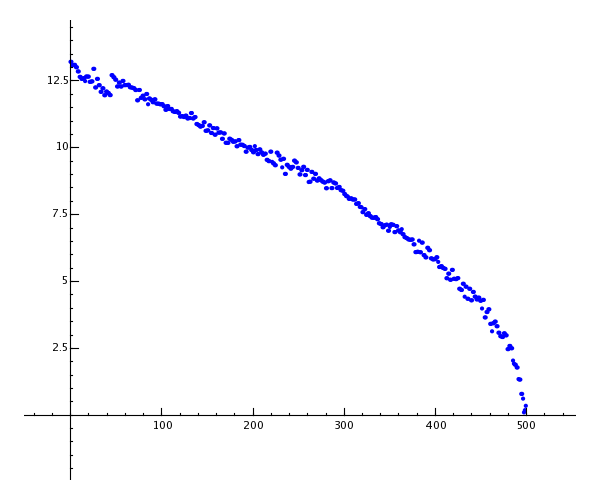
Il ne faut que quelques secondes à Sage pour calculer les valeurs propres de la matrice et en faire un graphique.
sage: e = m.eigenvalues() # environ 2 secondes
sage: w = [(i, abs(e[i])) for i in range(len(e))]
sage: show(points(w))
Grâce à la bibliothèque GMP (GNU Multiprecision Library), Sage peut effectuer des calculs sur de très grands nombres, comportant des millions ou des milliards de chiffres.
sage: factorial(100)
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
sage: n = factorial(1000000) # environ 2.5 secondes
Voici comment afficher les 100 première décimales de \(\pi\).
sage: N(pi, digits=100)
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068
Voici comment Sage factorise un polynôme en deux variables.
sage: R.<x,y> = QQ[]
sage: F = factor(x^99 + y^99)
sage: F
(x + y) * (x^2 - x*y + y^2) * (x^6 - x^3*y^3 + y^6) *
(x^10 - x^9*y + x^8*y^2 - x^7*y^3 + x^6*y^4 - x^5*y^5 +
x^4*y^6 - x^3*y^7 + x^2*y^8 - x*y^9 + y^10) *
(x^20 + x^19*y - x^17*y^3 - x^16*y^4 + x^14*y^6 + x^13*y^7 -
x^11*y^9 - x^10*y^10 - x^9*y^11 + x^7*y^13 + x^6*y^14 -
x^4*y^16 - x^3*y^17 + x*y^19 + y^20) * (x^60 + x^57*y^3 -
x^51*y^9 - x^48*y^12 + x^42*y^18 + x^39*y^21 - x^33*y^27 -
x^30*y^30 - x^27*y^33 + x^21*y^39 + x^18*y^42 - x^12*y^48 -
x^9*y^51 + x^3*y^57 + y^60)
sage: F.expand()
x^99 + y^99
Il ne faut pas plus de 5 secondes à Sage pour calculer le nombre de façons de partitionner mille millions (\(10^8\)) comme une somme d’entiers positifs.
sage: z = Partitions(10^8).cardinality() # environ 4.5 secondes
sage: str(z)[:40]
'1760517045946249141360373894679135204009'
Les algorithmes inclus dans Sage¶
Quand vous utilisez Sage, vous avez accès à l’une des plus grandes collections Open Source d’algorithmes de calcul.