Name
syslin — linear system definition
Calling Sequence
[sl]=syslin(dom,A,B,C [,D [,x0] ]) [sl]=syslin(dom,N,D) [sl]=syslin(dom,H)
Parameters
- dom
character string (
'c','d'), or[]or a scalar.- A,B,C,D
matrices of the state-space representation (
Doptional with default value zero matrix). For improper systemsDis a polynomial matrix.- x0
vector (initial state; default value is
0)- N, D
polynomial matrices
- H
rational matrix or linear state space representation
- sl
tlist ("
syslin" list) representing the linear system
Description
syslin defines a linear system as a list and
checks consistency of data.
dom specifies the time domain of the system and
can have the following values:
dom='c' for a continuous time system,
dom='d' for a discrete time system,
n for a sampled system with sampling period
n (in seconds).
dom=[] if the time domain is undefined
State-space representation:
sl=syslin(dom,A,B,C [,D [,x0] ])
represents the system :
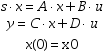
The output of syslin is a list of the following
form:
sl=tlist(['lss','A','B','C','D','X0','dt'],A,B,C,D,x0,dom)
Note that D is allowed to be a polynomial matrix
(improper systems).
Transfer matrix representation:
sl=syslin(dom,N,D)
sl=syslin(dom,H)
The output of syslin is a list of the following
form : sl=tlist(['r','num','den','dt'],N,D,dom) or
sl=tlist(['r','num','den','dt'],H(2),H(3),dom).
Linear systems defined as syslin can be
manipulated as usual matrices (concatenation, extraction, transpose,
multiplication, etc) both in state-space or transfer
representation.
Most of state-space control functions receive a
syslin list as input instead of the four matrices
defining the system.
Examples
A=[0,1;0,0];B=[1;1];C=[1,1];
S1=syslin('c',A,B,C) //Linear system definition
S1("A") //Display of A-matrix
S1("X0"), S1("dt") // Display of X0 and time domain
s=poly(0,'s');
D=s;
S2=syslin('c',A,B,C,D)
H1=(1+2*s)/s^2, S1bis=syslin('c',H1)
H2=(1+2*s+s^3)/s^2, S2bis=syslin('c',H2)
S1+S2
[S1,S2]
ss2tf(S1)-S1bis
S1bis+S2bis
S1*S2bis
size(S1)