Scilab 6.0.0
Справка Scilab >> Statistics > cdf > binomial
binomial
вероятности по биномиальному распределению
Последовательность вызова
pr=binomial(p,n)
Аргументы
- pr
вектор-строка с количеством элементов n+1
- p
вещественное число в диапазоне [0,1]
- n
целое число >= 1
Описание
pr=binomial(p,n) возвращает вектор вероятности по биномиальному распределению, т. е. pr(k+1) равно вероятности k "успехов" в n независимых экспериментах с вероятностью "успеха" в каждом из них p. Другими словами: pr(k+1) = вероятности (X=k), где X - случайное значение по распределению B(n,p), и численно:
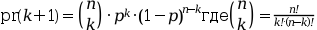
Примеры
// первый пример n=10;p=0.3; clf(); plot2d3(0:n,binomial(p,n)); // второй пример n=50;p=0.4; mea=n*p; sigma=sqrt(n*p*(1-p)); x=( (0:n)-mea )/sigma; clf() plot2d(x, sigma*binomial(p,n)); deff('y=Gauss(x)','y=1/sqrt(2*%pi)*exp(-(x.^2)/2)') plot2d(x, Gauss(x), style=2); // по формуле бинома (Осторожно, если n велико) function pr=binomial2(p, n) x=poly(0,'x');pr=coeff((1-p+x)^n).*horner(x^(0:n),p); endfunction p=1/3;n=5; binomial(p,n)-binomial2(p,n) // по Гамма-функции: gamma(n+1)=n! (Осторожно, если n велико) p=1/3;n=5; Cnks=gamma(n+1)./(gamma(1:n+1).*gamma(n+1:-1:1)); x=poly(0,'x'); pr=Cnks.*horner(x.^(0:n).*(1-x)^(n:-1:0),p); pr-binomial(p,n)
Comments
Add a comment:
Please login to comment this page.