Graph Structures¶

Theano represents symbolic mathematical computations as graphs. These graphs are composed of interconnected Apply and Variable nodes. They are associated to function application and data, respectively. Operations are represented by Op instances and data types are represented by Type instances. Here is a piece of code and a diagram showing the structure built by that piece of code. This should help you understand how these pieces fit together:

Code

import theano.tensor as T

x = T.dmatrix('x')
y = T.dmatrix('y')
z = x + y

Diagram

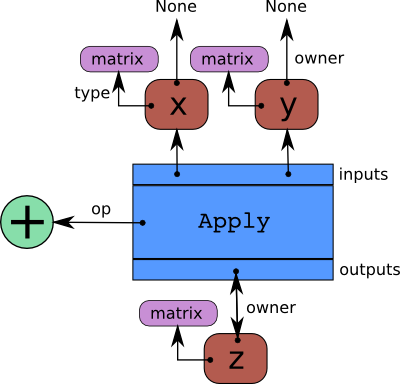
Arrows represent references to the Python objects pointed at. The blue box is an Apply node. Red boxes are Variable nodes. Green circles are Ops. Purple boxes are Types.

When we create Variables and then Apply Ops to them to make more Variables, we build a bi-partite, directed, acyclic graph. Variables point to the Apply nodes representing the function application producing them via their owner field. These Apply nodes point in turn to their input and output Variables via their inputs and outputs fields. (Apply instances also contain a list of references to their outputs, but those pointers don’t count in this graph.)

The owner field of both x and y point to None because they are not the result of another computation. If one of them was the result of another computation, it’s owner field would point to another blue box like z does, and so on.

Note that the Apply instance’s outputs points to z, and z.owner points back to the Apply instance.

An explicit example¶

In this example we will compare two ways of defining the same graph. First, a short bit of code will build an expression (graph) the normal way, with most of the graph construction being done automatically. Second, we will walk through a longer re-coding of the same thing without any shortcuts, that will make the graph construction very explicit.

Short example

This is what you would normally type:

# create 3 Variables with owner = None
x = T.matrix('x')
y = T.matrix('y')
z = T.matrix('z')

# create 2 Variables (one for 'e', one intermediate for y*z)
# create 2 Apply instances (one for '+', one for '*')
e = x + y * z

Long example

This is what you would type to build the graph explicitly:

from theano.tensor import add, mul, Apply, Variable, Constant, TensorType

# Instantiate a type that represents a matrix of doubles
float64_matrix = TensorType(dtype='float64',              # double
                            broadcastable=(False, False)) # matrix

 # We make the Variable instances we need.
x = Variable(type=float64_matrix, name='x')
y = Variable(type=float64_matrix, name='y')
z = Variable(type=float64_matrix, name='z')

# This is the Variable that we want to symbolically represents y*z
mul_variable = Variable(type=float64_matrix)
assert mul_variable.owner is None

# Instantiate a symbolic multiplication
node_mul = Apply(op=mul,
                 inputs=[y, z],
                 outputs=[mul_variable])
# Fields 'owner' and 'index' are set by Apply
assert mul_variable.owner is node_mul
# 'index' is the position of mul_variable in mode_mul's outputs
assert mul_variable.index == 0

# This is the Variable that we want to symbolically represents x+(y*z)
add_variable = Variable(type=float64_matrix)
assert add_variable.owner is None

# Instantiate a symbolic addition
node_add = Apply(op=add,
                 inputs=[x, mul_variable],
                 outputs=[add_variable])
# Fields 'owner' and 'index' are set by Apply
assert add_variable.owner is node_add
assert add_variable.index == 0

e = add_variable

# We have access to x, y and z through pointers
assert e.owner.inputs[0] is x
assert e.owner.inputs[1] is mul_variable
assert e.owner.inputs[1].owner.inputs[0] is y
assert e.owner.inputs[1].owner.inputs[1] is z

Note how the call to Apply modifies the owner and index fields of the Variables passed as outputs to point to itself and the rank they occupy in the output list. This whole machinery builds a DAG (Directed Acyclic Graph) representing the computation, a graph that Theano can compile and optimize.

Automatic wrapping¶

All nodes in the graph must be instances of Apply or Result, but <Op subclass>.make_node() typically wraps constants to satisfy those constraints. For example, the tensor.add() Op instance is written so that:

e = T.dscalar('x') + 1

builds the following graph:

node = Apply(op=add,
             inputs=[Variable(type=T.dscalar, name='x'),
                     Constant(type=T.lscalar, data=1)],
             outputs=[Variable(type=T.dscalar)])
e = node.outputs[0]

Graph Structures¶

The following section outlines each type of structure that may be used in a Theano-built computation graph. The following structures are explained: Apply, Constant, Op, Variable and Type.

Apply¶

An Apply node is a type of internal node used to represent a computation graph in Theano. Unlike Variable nodes, Apply nodes are usually not manipulated directly by the end user. They may be accessed via a Variable’s owner field.

An Apply node is typically an instance of the Apply class. It represents the application of an Op on one or more inputs, where each input is a Variable. By convention, each Op is responsible for knowing how to build an Apply node from a list of inputs. Therefore, an Apply node may be obtained from an Op and a list of inputs by calling Op.make_node(*inputs).

Comparing with the Python language, an Apply node is Theano’s version of a function call whereas an Op is Theano’s version of a function definition.

An Apply instance has three important fields:

op: An Op that determines the function/transformation being applied here.
inputs: A list of Variables that represent the arguments of the function.
outputs: A list of Variables that represent the return values of the function.

An Apply instance can be created by calling gof.Apply(op, inputs, outputs).

Op¶

An Op in Theano defines a certain computation on some types of inputs, producing some types of outputs. It is equivalent to a function definition in most programming languages. From a list of input Variables and an Op, you can build an Apply node representing the application of the Op to the inputs.

It is important to understand the distinction between an Op (the definition of a function) and an Apply node (the application of a function). If you were to interpret the Python language using Theano’s structures, code going like def f(x): ... would produce an Op for f whereas code like a = f(x) or g(f(4), 5) would produce an Apply node involving the f Op.

Type¶

A Type in Theano represents a set of constraints on potential data objects. These constraints allow Theano to tailor C code to handle them and to statically optimize the computation graph. For instance, the irow type in the theano.tensor package gives the following constraints on the data the Variables of type irow may contain:

Must be an instance of numpy.ndarray: isinstance(x, numpy.ndarray)
Must be an array of 32-bit integers: str(x.dtype) == 'int32'
Must have a shape of 1xN: len(x.shape) == 2 and x.shape[0] == 1

Knowing these restrictions, Theano may generate C code for addition, etc. that declares the right data types and that contains the right number of loops over the dimensions.

Note that a Theano Type is not equivalent to a Python type or class. Indeed, in Theano, irow and dmatrix both use numpy.ndarray as the underlying type for doing computations and storing data, yet they are different Theano Types. Indeed, the constraints set by dmatrix are:

Must be an instance of numpy.ndarray: isinstance(x, numpy.ndarray)
Must be an array of 64-bit floating point numbers: str(x.dtype) == 'float64'
Must have a shape of MxN, no restriction on M or N: len(x.shape) == 2

These restrictions are different from those of irow which are listed above.

There are cases in which a Type can fully correspond to a Python type, such as the double Type we will define here, which corresponds to Python’s float. But, it’s good to know that this is not necessarily the case. Unless specified otherwise, when we say “Type” we mean a Theano Type.

Variable¶

A Variable is the main data structure you work with when using Theano. The symbolic inputs that you operate on are Variables and what you get from applying various Ops to these inputs are also Variables. For example, when I type

>>> import theano
>>> x = theano.tensor.ivector()
>>> y = -x

x and y are both Variables, i.e. instances of the Variable class. The Type of both x and y is theano.tensor.ivector.

Unlike x, y is a Variable produced by a computation (in this case, it is the negation of x). y is the Variable corresponding to the output of the computation, while x is the Variable corresponding to its input. The computation itself is represented by another type of node, an Apply node, and may be accessed through y.owner.

More specifically, a Variable is a basic structure in Theano that represents a datum at a certain point in computation. It is typically an instance of the class Variable or one of its subclasses.

A Variable r contains four important fields:

type: a Type defining the kind of value this Variable can hold in computation.
owner: this is either None or an Apply node of which the Variable is an output.
index: the integer such that owner.outputs[index] is r (ignored if owner is None)
name: a string to use in pretty-printing and debugging.

Variable has one special subclass: Constant.

Constant¶

A Constant is a Variable with one extra field, data (only settable once). When used in a computation graph as the input of an Op application, it is assumed that said input will always take the value contained in the constant’s data field. Furthermore, it is assumed that the Op will not under any circumstances modify the input. This means that a constant is eligible to participate in numerous optimizations: constant inlining in C code, constant folding, etc.

A constant does not need to be specified in a function‘s list of inputs. In fact, doing so will raise an exception.

Graph Structures Extension¶

When we start the compilation of a Theano function, we compute some extra information. This section describes a portion of the information that is made available. Not everything is described, so email theano-dev if you need something that is missing.

The graph gets cloned at the start of compilation, so modifications done during compilation won’t affect the user graph.

Each variable receives a new field called clients. It is a list with references to every place in the graph where this variable is used. If its length is 0, it means the variable isn’t used. Each place where it is used is described by a tuple of 2 elements. There are two types of pairs:

The first element is an Apply node.
The first element is the string “output”. It means the function outputs this variable.

In both types of pairs, the second element of the tuple is an index, such that: var.clients[*][0].inputs[index] or fgraph.outputs[index] is that variable.

>>> import theano
>>> v = theano.tensor.vector()
>>> f = theano.function([v], (v+1).sum())
>>> theano.printing.debugprint(f)
Sum{acc_dtype=float64} [@A] ''   1
 |Elemwise{add,no_inplace} [@B] ''   0
   |TensorConstant{(1,) of 1.0} [@C]
   |<TensorType(float64, vector)> [@D]
>>> # Sorted list of all nodes in the compiled graph.
>>> topo = f.maker.fgraph.toposort()
>>> topo[0].outputs[0].clients
[(Sum{acc_dtype=float64}(Elemwise{add,no_inplace}.0), 0)]
>>> topo[1].outputs[0].clients
[('output', 0)]

>>> # An internal variable
>>> var = topo[0].outputs[0]
>>> client = var.clients[0]
>>> client
(Sum{acc_dtype=float64}(Elemwise{add,no_inplace}.0), 0)
>>> type(client[0])
<class 'theano.gof.graph.Apply'>
>>> assert client[0].inputs[client[1]] is var

>>> # An output of the graph
>>> var = topo[1].outputs[0]
>>> client = var.clients[0]
>>> client
('output', 0)
>>> assert f.maker.fgraph.outputs[client[1]] is var

Table Of Contents

Previous topic

Next topic

This Page

Graph Structures¶

An explicit example¶

Automatic wrapping¶

Graph Structures¶

Apply¶

Op¶

Type¶

Variable¶

Constant¶

Graph Structures Extension¶