Xiaozhou Steve Li, Yang Richard Yang, Mohamed G. Gouda, Simon S. Lam
Department of Computer Sciences
University of Texas at Austin
Austin, TX 78712-1188
{xli,yangyang,gouda,lam}@cs.utexas.edu
Copyright is held by the author/owner.
WWW10, May 2-5, 2001, Hong Kong
ACM 1-58113-348-0/01/0005.
Many emerging web and Internet applications are based on a group
communications model. Thus, securing group communications is an
important Internet design issue. The key graph approach has
been proposed for group key management. Key tree and key star are two
important types of key graphs. Previous work has been focused on
individual rekeying, i.e., rekeying after each join or leave request.
In this paper, we first identify two problems with individual
rekeying: inefficiency and an out-of-sync problem between keys and
data. We then propose the use of periodic batch rekeying which
can improve efficiency and alleviate the out-of-sync problem. We
devise a marking algorithm to process a batch of join and leave
requests. We then analyze the key server's processing cost for batch
rekeying. Our results show that batch rekeying, compared to individual
rekeying, saves server cost substantially. We also show that when the
number of requests in a batch is not large, the best key tree degree
is four; otherwise, key star (a special key tree with root degree
equal to group size) outperforms small-degree key trees.
Keywords: Secure group communications, group key management, rekeying.
Many emerging web applications are based on a group communications model [12,4,15]. In the Internet, multicast has been used successfully to provide an efficient, best-effort delivery service from a sender to a large group of receivers [6]. Thus, securing group communications (i.e., providing confidentiality, authenticity, and integrity of messages delivered between group members) will become an important Internet design issue.
One way to achieve secure group communications is to have a symmetric key, called group key, shared only by group members (also called users in this paper). The group key is distributed by a key server which provides group key management service. Messages sent by a member to the group are encrypted with the group key, so that only members of the group can decrypt and read the messages.
Compared to two-party communications, a unique characteristic of group communications is that group membership can change over time: new users can join and current users can leave or be expelled. If a user wants to join the group, it sends a join request to the key server. The user and key server mutually authenticate each other using a protocol such as SSL [7]. If authenticated and accepted into the group, the user shares with the key server a symmetric key, called the user's individual key.
For a group of ![]() users, initially distributing the group key to all
users requires
users, initially distributing the group key to all
users requires ![]() messages each encrypted with an individual key (the
computation and communication costs are proportional to group size
messages each encrypted with an individual key (the
computation and communication costs are proportional to group size
![]() ). To prevent a new user from reading past communications (called
backward access control) and a departed user from reading future
communications (called forward access control), the key server may
rekey (change the group key) whenever group membership
changes. For large groups, join and leave requests can happen
frequently. Thus, a group key management service should be scalable
with respect to frequent key changes.
). To prevent a new user from reading past communications (called
backward access control) and a departed user from reading future
communications (called forward access control), the key server may
rekey (change the group key) whenever group membership
changes. For large groups, join and leave requests can happen
frequently. Thus, a group key management service should be scalable
with respect to frequent key changes.
It is easier to rekey after a join than a leave. After a join, the
new group key can be sent via unicast to the new member (encrypted
with its individual key) and via multicast to existing members
(encrypted with the previous group key). After a leave, however,
since the previous group key cannot be used, the new group key may be
securely distributed by encrypting it with individual keys. This
straightforward approach, however, is not scalable. In particular,
rekeying costs 2 encryptions for a join and ![]() encryptions for a
leave, where
encryptions for a
leave, where ![]() is current group size (see
Section 2.2).
is current group size (see
Section 2.2).
The key graph approach [16,17] has been proposed for
scalable rekeying. In this approach, besides the group key and its
individual key, each user is given several auxiliary keys.
These auxiliary keys are used to facilitate rekeying. Key graph
is a data structure that models user-key and key-key
relationships. Key tree is an important type of key graph where
key-key relationships are modeled as a tree. For a single leave
request, key tree reduces server processing cost to ![]() . Key star is a special case of key tree. We provide more details of
the key graph approach in Section 2.
. Key star is a special case of key tree. We provide more details of
the key graph approach in Section 2.
A thorough performance analysis of individual rekeying (rekeying after each join or leave) is given in [17]. Individual rekeying, however, has two problems. First, it is relatively inefficient. Second, there is an out-of-sync problem between keys and data (see Section 4).
In this paper, we propose the use of periodic batch rekeying that can improve efficiency and alleviate the out-of-sync problem. In batch rekeying, the key server collects join and leave requests in a period of time and rekeys after a batch has been collected. We devise a marking algorithm to process a batch of requests. We then analyze the worst case and average case server processing costs for batch rekeying. Our results show that batch rekeying, compared to individual rekeying, saves server cost substantially. We also show that when the size of a batch is not large (roughly, when the number of joins is less than half of current group size, and the number of leaves is less than a quarter of current group size), four is the best key tree degree; otherwise, key star outperforms small-degree key trees. Our results provide guidelines for a key server to choose an appropriate data structure for group key management.
This paper is organized as follows. Section 2 briefly reviews the key graph approach. Section 3 identifies two problems with individual rekeying. Section 4 presents the batch rekeying idea. Section 5 presents the marking algorithm. Section 6 analyzes the server's processing cost for batch rekeying. Section 7 shows how to minimize server cost. Section 8 discusses related work. Section 9 concludes the paper.
The key graph approach [17] assumes that there is a single
trusted and secure key server, and the key server uses a key graph for
group key management. Key graph is a directed acyclic graph with two
types of nodes: u-nodes, which represent users, and k-nodes, which
represent keys. User ![]() is given key
is given key ![]() if and only if there is a
directed path from u-node
if and only if there is a
directed path from u-node ![]() to k-node
to k-node ![]() in the key graph. Key tree
and key star are two important types of key graph. In a key tree, the
k-nodes and u-nodes are organized as a tree. Key star is a special key
tree where tree degree equals group size. To avoid confusion, from now
on, we use key tree to mean small-degree key tree. We only consider
key tree and key star in this paper.
in the key graph. Key tree
and key star are two important types of key graph. In a key tree, the
k-nodes and u-nodes are organized as a tree. Key star is a special key
tree where tree degree equals group size. To avoid confusion, from now
on, we use key tree to mean small-degree key tree. We only consider
key tree and key star in this paper.
In a key tree, the root is the group key, leaf nodes are individual
keys, and the other nodes are auxiliary keys. Consider a group of 9
users ![]() , ...,
, ..., ![]() . A key tree of degree 3 is shown in
Figure 2.1(a). In this figure, boxes represent u-nodes
and circles represent k-nodes. User
. A key tree of degree 3 is shown in
Figure 2.1(a). In this figure, boxes represent u-nodes
and circles represent k-nodes. User ![]() is given 3 keys on the path
from
is given 3 keys on the path
from ![]() to
to ![]() :
: ![]() ,
, ![]() , and
, and ![]() .
. ![]() is the group key.
is the group key. ![]() is
is ![]() 's individual key, which is shared by
only
's individual key, which is shared by
only ![]() and the key server.
and the key server. ![]() is an auxiliary key shared by
is an auxiliary key shared by
![]() ,
, ![]() , and
, and ![]() .
.
|
|
: |
|
|
|
Here
![]() means key
means key ![]() encrypted with key
encrypted with key ![]() . We call each
item in the rekey message an encrypted key. Upon receiving the
rekey message, a user extracts the encrypted keys that it needs. For
example,
. We call each
item in the rekey message an encrypted key. Upon receiving the
rekey message, a user extracts the encrypted keys that it needs. For
example, ![]() only needs
only needs
![]() and
and
![]() .
.
Similarly, suppose ![]() wants to join a group of 8 users (from
Figure 2.1(b) to 2.1(a)). The key server
finds a joining point (
wants to join a group of 8 users (from
Figure 2.1(b) to 2.1(a)). The key server
finds a joining point (![]() in this example) for the new user,
constructs the rekey message, multicasts it to the whole group, and
unicasts
in this example) for the new user,
constructs the rekey message, multicasts it to the whole group, and
unicasts ![]() the keys needed by
the keys needed by ![]() :
:
|
|
: |
|
|
|
: |
|
From the above example, we can see that both the server's computation
and communication costs are proportional to the number of encryptions
to be performed (5 for the first example and 4 for the second
example). Thus, we use server cost to mean the number of
encryptions the key server has to perform. If the key tree degree is
![]() and there are
and there are ![]() users, assuming the key tree is a completely
balanced tree, the server cost is
users, assuming the key tree is a completely
balanced tree, the server cost is
![]() for a join and
for a join and
![]() for a leave. [17] showed that
for a leave. [17] showed that ![]() is the
optimal degree for a leave.
is the
optimal degree for a leave.
Key star is a special case of key tree where tree root degree equals
group size. Key star models the straightforward approach. In key
star, every user has two keys: its individual key and the group
key. There is no auxiliary key. Figure 2(a) shows the
key star for 4 users. Suppose ![]() wants to leave the group (from
Figure 2(a) to 2(b)), the key server
encrypts the new group key
wants to leave the group (from
Figure 2(a) to 2(b)), the key server
encrypts the new group key ![]() using every user's individual
key, puts the encrypted keys in a message and multicasts it to the
whole group:
using every user's individual
key, puts the encrypted keys in a message and multicasts it to the
whole group:
|
|
: |
|
Suppose ![]() wants to join the group (from Figure 2(b) to
2(a)), the key server sends out the following
messages:
wants to join the group (from Figure 2(b) to
2(a)), the key server sends out the following
messages:
|
|
: |
|
|
|
: |
|
Clearly, using a key star, the server cost is ![]() for a join and
for a join and ![]() for a leave.
for a leave.
Ideally, a departed user should be expelled from the group, and a new user be accepted to the group, as early as possible. Thus, the key server should rekey immediately after receiving a join or leave request, We call this individual rekeying. Individual rekeying, however, has two problems: inefficiency and an out-of-sync problem between keys and data.
Individual rekeying is relatively inefficient for two reasons. First, the rekey message has to be signed for authentication purpose, otherwise a compromised group user can send out bogus rekey messages and mess up the whole system. Signing operation is computationally expensive [18]. If, for every single request, the key server has to generate and sign a rekey message, the signing operation alone will place a heavy burden on the key server, especially when requests are frequent.
Second, consider two leaves that happen one after another. The key server generates two sets of new keys (group key and auxiliary keys) for these two leaves. These two leaves, however, might temporally happen so close to each other that the first set of new keys are actually not used and are immediately replaced by the second set of new keys. When requests are frequent, like during the startup or teardown of a multicast session, many new keys may be generated and distributed, while not used at all. This is a waste of server cost.
Individual rekeying also has the following out-of-sync problem
between keys and data: a user might receive a data message encrypted
by an old group key, or it might receive a data message encrypted with a
group key that it has not received yet. Figure 3
shows an example of this problem. In this example, at time ![]() ,
,
![]() receives a data message encrypted with group key GK(2) from
receives a data message encrypted with group key GK(2) from ![]() ,
but
,
but ![]() has not received GK(2); at time
has not received GK(2); at time ![]() ,
, ![]() receives a data
message encrypted with group key GK(0) from
receives a data
message encrypted with group key GK(0) from ![]() , but
, but ![]() 's current
group key is GK(2). Delay of reliable rekey message delivery
2 can be large and
variable. Thus, this out-of-sync problem may require a user to keep
many old group keys, and/or buffer a large amount of data encrypted with
group keys that it has not received.
's current
group key is GK(2). Delay of reliable rekey message delivery
2 can be large and
variable. Thus, this out-of-sync problem may require a user to keep
many old group keys, and/or buffer a large amount of data encrypted with
group keys that it has not received.
To address the above two problems, we propose the use of periodic batch rekeying. In batch rekeying, the key server waits for a period
of time, called a rekey interval, collects all the join and
leave requests during the interval, generates new keys, constructs a
rekey message, and multicasts the rekey message.
Batch rekeying improves efficiency because it reduces the number of rekey messages to be signed: one for a batch of requests, instead of one for each. Batch rekeying also takes advantage of the possible overlap of new keys for multiple rekey requests, and thus reduces the possibility of generating new keys that will not be used. In Section 6, we will quantify the performance benefit of batch rekeying.
Batch rekeying alleviates the out-of-sync problem. To see this, let
![]() be the maximum delay of reliable delivery of rekey messages,
be the maximum delay of reliable delivery of rekey messages,
![]() be the maximum delay of data messages,
be the maximum delay of data messages, ![]() be the length of the
rekey interval, and GK(
be the length of the
rekey interval, and GK(![]() ) be the
) be the ![]() -th group key. That is, if a
user's current group key is GK(
-th group key. That is, if a
user's current group key is GK(![]() ), when it receives a rekey message,
its group key becomes GK(
), when it receives a rekey message,
its group key becomes GK(![]() ). It is not hard to show the following
theorem. We skip the proof for simplicity.
). It is not hard to show the following
theorem. We skip the proof for simplicity.
This theorem indicates that if we make ![]() relatively large compared
to
relatively large compared
to ![]() and
and ![]() , then a user only needs to keep GK(
, then a user only needs to keep GK(![]() ), GK(
), GK(![]() ),
and its current auxiliary keys. If the user receives a data message
encrypted with GK(
),
and its current auxiliary keys. If the user receives a data message
encrypted with GK(![]() ), it has to keep them in some buffer and wait
until the next rekey message arrives. Since the rekey interval is
likely to be larger than message delays, the condition
), it has to keep them in some buffer and wait
until the next rekey message arrives. Since the rekey interval is
likely to be larger than message delays, the condition
![]() is easy to satisfy.
is easy to satisfy.
Batch rekeying is a tradeoff between performance and security. Since the key server does not rekey immediately, a departed user will remain in the group longer, and a new user has to wait longer to be accepted to the group.
We define vulnerability window to be the period of time from the
key server receives a join or leave request, to all users receive the
rekey message. We use the maximum size of vulnerability window,
denoted as ![]() , to measure security, because any group traffic sent
within the vulnerability window is susceptible to be read by a
departed user. The smaller
, to measure security, because any group traffic sent
within the vulnerability window is susceptible to be read by a
departed user. The smaller ![]() , the more secure the system is. We note
that
, the more secure the system is. We note
that ![]() also measures how soon a new user can be accepted to the
group.
also measures how soon a new user can be accepted to the
group.
Figure 4(a) shows an example to illustrate the
vulnerability window notion for individual rekeying. In this example,
![]() requests to leave the group at
requests to leave the group at ![]() . The key server receives
the request at
. The key server receives
the request at ![]() and rekeys immediately. The rekey message arrives
and rekeys immediately. The rekey message arrives
![]() at
at ![]() . But between
. But between ![]() and
and ![]() ,
, ![]() sends out a message
encrypted with GK(0) at
sends out a message
encrypted with GK(0) at ![]() . The message arrives
. The message arrives ![]() at
at
![]() . Although
. Although ![]() has left the group at
has left the group at ![]() , it is still able to read
this message. The period between
, it is still able to read
this message. The period between ![]() and
and ![]() is the vulnerability
window. Figure 4(b) shows the vulnerability window
notion for batch rekeying.
is the vulnerability
window. Figure 4(b) shows the vulnerability window
notion for batch rekeying.
It is not hard to see that ![]() for individual rekeying and
for individual rekeying and
![]() for batch rekeying. So even in individual rekeying, a
departed user is able to continue reading group communication for some
period of time. Batch rekeying only makes this period longer and
adjustable. Many applications can tolerate such a compromise. For
example, a pay-per-view application can tolerate a viewer remaining in
the group for a few more minutes after its subscription expires. An
application can choose an acceptable
for batch rekeying. So even in individual rekeying, a
departed user is able to continue reading group communication for some
period of time. Batch rekeying only makes this period longer and
adjustable. Many applications can tolerate such a compromise. For
example, a pay-per-view application can tolerate a viewer remaining in
the group for a few more minutes after its subscription expires. An
application can choose an acceptable ![]() based on its own
requirements.
based on its own
requirements.
As noted in the Introduction section, it is easier to rekey after a join than a leave. Thus, the access delay of a new user may be reduced by processing each new join immediately without rekeying the entire group, i.e., each new user is given the current group key and its auxiliary keys encrypted with its individual key, but leave requests are processed periodically in a batch. This approach offers new users faster access to the group at the cost of also giving new users a small amount of backward access. For simplicity, we will not discuss this approach in detail in the balance of this paper.
In this section, we present a marking algorithm for the key server to process a batch of requests. Obviously, if the key server uses key star, batch rekeying is a straightforward extension to individual rekeying. Thus, the marking algorithm applies to key tree only. In Section 6, we will analyze the resulting server processing cost for batch rekeying.
We use ![]() to denote the number of joins in a batch and
to denote the number of joins in a batch and ![]() to denote
the number of leaves in a batch. We assume that within a batch, a user
will not first join then leave, or first leave then join.
to denote
the number of leaves in a batch. We assume that within a batch, a user
will not first join then leave, or first leave then join.
Given a batch of requests, the main task for the key server is to identify which keys should be added, deleted, or changed. In individual rekeying, all the keys on the path from the request location to the root of the key tree have to be changed. When there are multiple requests, there are multiple paths. These paths form a subtree, called rekey subtree, which includes all the keys to be added or changed. The rekey subtree does not include individual keys.
The key server cannot control which users might leave, but it can control where in the key tree to place the new users. Thus, the key server should carefully place the new users (if there were any) so that the number of encryptions it has to perform is minimized. The following marking algorithm uses some heuristics to achieve this objective. Figure 5 illustrates the idea. We use the word key and node interchangeably.
UPDATE.
UPDATE or DELETE. Those
leaving nodes without joining replacements are marked
DELETE. A non-leaf node is marked DELETE if and
only if all of its children are marked DELETE.
NEW and mark all
the nodes from the root to the parent of UPDATE.
NEW and mark all
the keys from the replacement locations (except the old
location of UPDATE.
After marking the key tree, the key server removes all nodes that are
marked DELETE. The nodes marked UPDATE or
NEW form the rekey subtree. The key server then traverses the
rekey subtree, generates new keys, encrypts every new key by each of
its children, constructs and multicasts the rekey message. It is not
hard to see that the running time of the marking algorithm is
![]() , which is efficient (simulation results in
section 6.3).
, which is efficient (simulation results in
section 6.3).
Figure 6 shows an example to illustrate the
marking algorithm. In this example, ![]() and
and ![]() leave the group,
leave the group,
![]() joins the group. The rekey subtree is marked as in the
figure. Using group-oriented rekeying, the key server multicasts the
following message to the group:
joins the group. The rekey subtree is marked as in the
figure. Using group-oriented rekeying, the key server multicasts the
following message to the group:
|
|
: |
|
|
|
Figure 7 shows another example. In this example,
![]() leaves the group,
leaves the group, ![]() and
and ![]() join the group. The rekey
subtree is marked as in the figure. Using group-oriented rekeying, the
key server multicasts the following message to the group:
join the group. The rekey
subtree is marked as in the figure. Using group-oriented rekeying, the
key server multicasts the following message to the group:
|
|
: |
|
|
|
To achieve best performance, a key tree should be kept more or less balanced. Our marking algorithm aims to keep the tree balanced across multiple batches, by adding extra joins to the shallowest leaf node of the tree in each batch.
However, depending on the actual locations of the requests, even if the key tree starts complete and balanced, it is possible that the key tree may grow unbalanced after some number of batches. For example, many users located close to each other in the key tree may decide to leave at the same time. It is impossible to keep the key tree balanced all the time, without incurring extra cost. We refer the interested reader to [14] for discussions on this topic.
In this section, we analyze the server processing cost for batch rekeying. We consider the worst case and average case and compare batch rekeying against individual rekeying.
Key star's batch rekeying server cost, denoted as
![]() , is:
, is:
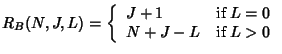
Thus, our analysis mainly focuses on key trees. For the purpose of analysis, we assume that the key tree is a complete and balanced tree at the beginning of a batch, and that each current user has equal probability of leaving.
Let ![]() be the key tree degree,
be the key tree degree, ![]() be the group size at the beginning
of a batch,
be the group size at the beginning
of a batch, ![]() be the height of the key tree (
be the height of the key tree (
![]() ),
),
![]() be the worst case batch rekeying server cost, and
be the worst case batch rekeying server cost, and
![]() be the average case batch rekeying server cost.
be the average case batch rekeying server cost.
The marking algorithm can control where to place joins, but cannot control where leaves happen. Thus, worst case analysis mainly considers how the locations of leaves affect the server cost. Since the marking algorithm takes different operations for four cases, worst case analysis is also divided into four cases.
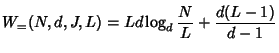
If ![]() is not some power of
is not some power of ![]() , suppose
, suppose ![]() ,
,
![]() , then in the worst case, each of the
, then in the worst case, each of the ![]() additional leaves
adds
additional leaves
adds ![]() to the total cost (see
Figure 6.1(b)). Thus,
to the total cost (see
Figure 6.1(b)). Thus,
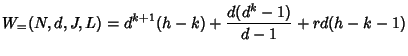
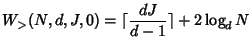
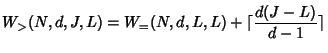
Figure 9 shows
![]() for
for
![]() and
and
![]()
![]()
![]() , on a wide range of
, on a wide range of ![]() and
and ![]() values. We can
see that, for fixed
values. We can
see that, for fixed ![]() ,
,
![]() is an increasing function of
is an increasing function of ![]() (because more joins helps the key tree to ``grow back''). For fixed
(because more joins helps the key tree to ``grow back''). For fixed
![]() , as
, as ![]() becomes larger,
becomes larger,
![]() first increases (because more
leaves means more keys to be changed), then decreases (because now
some keys are pruned from the tree). Clearly,
first increases (because more
leaves means more keys to be changed), then decreases (because now
some keys are pruned from the tree). Clearly,
![]() is an
increasing function of
is an
increasing function of ![]() . We will investigate the effect of
. We will investigate the effect of ![]() in
Section 7.
in
Section 7.
The server cost depends on the number of nodes belonging to the rekey subtree, and the number of children each node has. Thus, our technique for average case analysis is to consider the probability that an individual node belongs to the rekey subtree, and to consider the node's expected number of children (some children might be pruned). Again, we consider the following four cases.
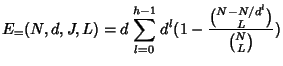 |
DELETE and pruned from the tree. A node
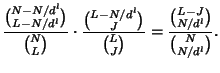
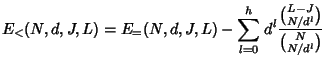 |
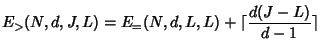 |
We built a simulator for the marking algorithm. The simulator first
constructs a key tree and randomly picks ![]() users to leave, it then
runs the marking algorithm and calculates the server cost. We ran the
simulation for
users to leave, it then
runs the marking algorithm and calculates the server cost. We ran the
simulation for ![]() times and calculated the mean server
cost. Simulations were done on a Sun Ultra Sparc I with 167MHz CPU and
128MB memory. The marking algorithm took at most
times and calculated the mean server
cost. Simulations were done on a Sun Ultra Sparc I with 167MHz CPU and
128MB memory. The marking algorithm took at most ![]() ms when
ms when
![]() , and at most
, and at most ![]() ms when
ms when
![]() , for all
, for all
![]() and
and ![]() .
.
Figure 11 shows
![]() for
for
![]() and
and
![]()
![]()
![]() , on a wide range of
, on a wide range of ![]() and
and ![]() values. Our
analysis and simulation results match so well that we cannot tell the
difference.
values. Our
analysis and simulation results match so well that we cannot tell the
difference.
Figure 12 compares average case and worst case server
costs. These two costs are rather close to each other when ![]() and
and ![]() are relatively small compared to
are relatively small compared to ![]() . Thus, we can consider worst case
a good approximation to average case.
. Thus, we can consider worst case
a good approximation to average case.
In this section, we show that batch rekeying saves server cost substantially over individual rekeying. The actual save depends on whether the key server uses key star or key tree.
Let
![]() be the cost for processing
be the cost for processing ![]() joins and
joins and
![]() leaves individually. Clearly,
leaves individually. Clearly,
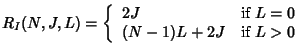
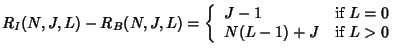
We have mentioned that using key tree for individual rekeying, the
server cost is
![]() for a leave and
for a leave and
![]() for a
join. Let
for a
join. Let
![]() be the server cost for rekeying a batch of
be the server cost for rekeying a batch of ![]() joins and
joins and ![]() leaves individually. Clearly,
leaves individually. Clearly,
Figure 13 compares batch rekeying against
individual rekeying for
![]() and
and
![]() . On the
left figure, we show a narrower range of
. On the
left figure, we show a narrower range of ![]() and
and ![]() values. On the
right figure, we show a wider range. We can see that batch rekeying
has a substantial benefit over individual rekeying.
values. On the
right figure, we show a wider range. We can see that batch rekeying
has a substantial benefit over individual rekeying.
In the previous section, we have shown that batch rekeying saves server cost substantially. But when a key server uses batch rekeying, there are still two questions to answer. Shall the key server use key tree or key star? If it uses key tree, what degree should be the key tree? In this section, we show that the choice of data structure has big influence on server cost, and we provide guidelines for the key server to choose an appropriate one.
First, we compare key star cost against ![]() -ary and
-ary and ![]() -ary key tree
costs. Figure 14 shows the comparison for
-ary key tree
costs. Figure 14 shows the comparison for ![]() and
and ![]() . The shadowed area is where key star is better. We
observe that key star is better when
. The shadowed area is where key star is better. We
observe that key star is better when ![]() or when
or when ![]() and
and ![]() are
large.
are
large.
Figure 15 compares key star cost against key tree
costs for ![]() ,
, ![]() , and
, and ![]() ,
,
![]() . We
temporarily ignore the case where
. We
temporarily ignore the case where ![]() . Each curve in the figures
corresponds to a
. Each curve in the figures
corresponds to a ![]() value. The curves are where key star cost is the
same as
value. The curves are where key star cost is the
same as ![]() -ary key tree cost. Above a curve is where key star is
better, while below a curve is where key tree is better. From this
figure we draw a similar conclusion that key star is better than key
tree when
-ary key tree cost. Above a curve is where key star is
better, while below a curve is where key tree is better. From this
figure we draw a similar conclusion that key star is better than key
tree when ![]() and
and ![]() are large. Roughly, when
are large. Roughly, when
![]() and
and
![]() , key tree is better than key star; otherwise, key
star is better than key tree.
, key tree is better than key star; otherwise, key
star is better than key tree.
[17] showed that ![]() is optimal for individual rekeying. We
show in this section that
is optimal for individual rekeying. We
show in this section that ![]() is still optimal for batch rekeying.
is still optimal for batch rekeying.
Since server cost depends on both ![]() and
and ![]() , we first look at the
special case when
, we first look at the
special case when ![]() . Figure 16 shows key tree
costs for various
. Figure 16 shows key tree
costs for various ![]() values, when
values, when ![]() . We can see that
. We can see that ![]() is
better than others when
is
better than others when ![]() and
and ![]() are small. Figure
17 shows the server costs for key trees with various
are small. Figure
17 shows the server costs for key trees with various
![]() values when
values when ![]() . We also observe that
. We also observe that ![]() is better than
others when
is better than
others when ![]() and
and ![]() are small. These two figures also show that
are small. These two figures also show that
![]() has a big influence on the resulting server cost. Figure
18 shows the area where
has a big influence on the resulting server cost. Figure
18 shows the area where ![]() is better than other
is better than other ![]() values. We can see that roughly, in the area where key tree is better
than key star,
values. We can see that roughly, in the area where key tree is better
than key star, ![]() is the best.
is the best.
From the above discussions we have seen that choosing an appropriate
data structure has big influence on server cost. An application
usually has an estimate of ![]() and
and ![]() , based on the expected number
of users, length of the rekey interval, and the application's other
characteristics. Thus, the guideline for a key server to choose an
appropriate data structure is: if
, based on the expected number
of users, length of the rekey interval, and the application's other
characteristics. Thus, the guideline for a key server to choose an
appropriate data structure is: if
![]() and
and
![]() ,
use a
,
use a ![]() -ary key tree; otherwise, use a key star.
-ary key tree; otherwise, use a key star.
The topic of secure group communications has been investigated in [2,3,8,10,9,13]. [13] addressed the need for frequent group key changes and the associated scalability problem. The approach proposed in [13] decomposes a large group of users into many subgroups and employs a hierarchy of group security agents. This approach, however, requires many trusted entities.
Approaches that assume only a single trusted key server are proposed in [17,16,1]. In these approaches, a user is given some auxiliary keys, besides the group key and the individual key, to reduce the server cost for rekeying. These approaches have been mainly focused on reducing the server cost for individual rekeying.
[5] addressed the problem of batch rekeying and proposed using boolean function minimization technique to facilitate batch rekeying. Their approach, however, has the collusion problem, namely, two users can combine their knowledge of keys to continue reading group communications, even after they leave the group.
[14] addressed the problem of keeping the key tree balanced. Their approach essentially is to add joins at the shallowest leaf nodes of the tree, and re-structure the tree periodically. [14] also briefly described an algorithm for batch rekeying, in which joins replace leaves one by one, and if there are still extra joins, they are added to the shallowest leaf nodes of the tree one by one. [14]'s objective is to keep the key tree balanced, while our marking algorithm aims to reduce the server cost for batch rekeying. [14] did not provide any quantitative analysis for the benefit of batch rekeying.
This paper addressed the scalability problem of group key management. We identified two problems with individual rekeying: inefficiency and an out-of-sync problem between keys and data. We proposed the use of periodic batch rekeying to improve the key server's performance and alleviate the out-of-sync problem. We devised a marking algorithm for the key server to process a batch of join and leave requests, and we analyzed the key server's processing cost for batch rekeying. Our results show that batch rekeying, compared to individual rekeying, saves server cost substantially. We also show that when the number of requests is not large in a batch, four is the best key tree degree; otherwise, key star outperforms small-degree key trees.
We thank the anonymous reviewers for helpful comments.