 |
Eigen
3.2.7
|
 |
Eigen
3.2.7
|
A general Cholesky factorization and solver based on Cholmod.
This class allows to solve for A.X = B sparse linear problems via a LL^T or LDL^T Cholesky factorization using the Cholmod library. The sparse matrix A must be selfadjoint and positive definite. The vectors or matrices X and B can be either dense or sparse.
This variant permits to change the underlying Cholesky method at runtime. On the other hand, it does not provide access to the result of the factorization. The default is to let Cholmod automatically choose between a simplicial and supernodal factorization.
| _MatrixType | the type of the sparse matrix A, it must be a SparseMatrix<> |
| _UpLo | the triangular part that will be used for the computations. It can be Lower or Upper. Default is Lower. |
This class supports all kind of SparseMatrix<>: row or column major; upper, lower, or both; compressed or non compressed.
 Inheritance diagram for CholmodDecomposition< _MatrixType, _UpLo >:
Inheritance diagram for CholmodDecomposition< _MatrixType, _UpLo >:Public Member Functions | |
| void | analyzePattern (const MatrixType &matrix) |
| cholmod_common & | cholmod () |
| CholmodDecomposition < _MatrixType, _UpLo > & | compute (const MatrixType &matrix) |
| void | factorize (const MatrixType &matrix) |
| ComputationInfo | info () const |
| Reports whether previous computation was successful. More... | |
| CholmodDecomposition < _MatrixType, _UpLo > & | setShift (const RealScalar &offset) |
| const internal::solve_retval < CholmodBase, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| const internal::sparse_solve_retval < CholmodBase, Rhs > | solve (const SparseMatrixBase< Rhs > &b) const |
|
inlineinherited |
Performs a symbolic decomposition on the sparsity pattern of matrix.
This function is particularly useful when solving for several problems having the same structure.
|
inlineinherited |
Returns a reference to the Cholmod's configuration structure to get a full control over the performed operations. See the Cholmod user guide for details.
|
inlineinherited |
Computes the sparse Cholesky decomposition of matrix
|
inlineinherited |
Performs a numeric decomposition of matrix
The given matrix must have the same sparsity pattern as the matrix on which the symbolic decomposition has been performed.
|
inlineinherited |
Reports whether previous computation was successful.
Success if computation was succesful, NumericalIssue if the matrix.appears to be negative.
|
inlineinherited |
Sets the shift parameter that will be used to adjust the diagonal coefficients during the numerical factorization.
During the numerical factorization, an offset term is added to the diagonal coefficients:
d_ii = offset + d_ii
The default is offset=0.
*this.
|
inlineinherited |
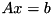 using the current decomposition of A.
using the current decomposition of A.
|
inlineinherited |
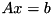 using the current decomposition of A.
using the current decomposition of A.