 |
Eigen
3.2.7
|
|
|
Eigen
3.2.7
|
|
Base class for all dense matrices, vectors, and expressions.
This class is the base that is inherited by all matrix, vector, and related expression types. Most of the Eigen API is contained in this class, and its base classes. Other important classes for the Eigen API are Matrix, and VectorwiseOp.
Note that some methods are defined in other modules such as the LU module LU module for all functions related to matrix inversions.
| Derived | is the derived type, e.g. a matrix type, or an expression, etc. |
When writing a function taking Eigen objects as argument, if you want your function to take as argument any matrix, vector, or expression, just let it take a MatrixBase argument. As an example, here is a function printFirstRow which, given a matrix, vector, or expression x, prints the first row of x.
This class can be extended with the help of the plugin mechanism described on the page Customizing/Extending Eigen by defining the preprocessor symbol EIGEN_MATRIXBASE_PLUGIN.
Inheritance diagram for MatrixBase< Derived >:Public Types | |
| enum | { RowsAtCompileTime, ColsAtCompileTime, SizeAtCompileTime, MaxRowsAtCompileTime, MaxColsAtCompileTime, MaxSizeAtCompileTime, IsVectorAtCompileTime, Flags, IsRowMajor , CoeffReadCost } |
| typedef internal::traits < Derived >::Index | Index |
| The type of indices. More... | |
| typedef Matrix< typename internal::traits< Derived > ::Scalar, internal::traits < Derived >::RowsAtCompileTime, internal::traits< Derived > ::ColsAtCompileTime, AutoAlign|(internal::traits < Derived >::Flags &RowMajorBit?RowMajor:ColMajor), internal::traits< Derived > ::MaxRowsAtCompileTime, internal::traits< Derived > ::MaxColsAtCompileTime > | PlainObject |
| The plain matrix type corresponding to this expression. More... | |
Public Member Functions | |
| const AdjointReturnType | adjoint () const |
| void | adjointInPlace () |
| bool | all (void) const |
| bool | allFinite () const |
| bool | any (void) const |
| template<typename EssentialPart > | |
| void | applyHouseholderOnTheLeft (const EssentialPart &essential, const Scalar &tau, Scalar *workspace) |
| template<typename EssentialPart > | |
| void | applyHouseholderOnTheRight (const EssentialPart &essential, const Scalar &tau, Scalar *workspace) |
| template<typename OtherDerived > | |
| void | applyOnTheLeft (const EigenBase< OtherDerived > &other) |
| template<typename OtherScalar > | |
| void | applyOnTheLeft (Index p, Index q, const JacobiRotation< OtherScalar > &j) |
| template<typename OtherDerived > | |
| void | applyOnTheRight (const EigenBase< OtherDerived > &other) |
| template<typename OtherScalar > | |
| void | applyOnTheRight (Index p, Index q, const JacobiRotation< OtherScalar > &j) |
| ArrayWrapper< Derived > | array () |
| const DiagonalWrapper< const Derived > | asDiagonal () const |
| template<typename CustomBinaryOp , typename OtherDerived > | |
| const CwiseBinaryOp < CustomBinaryOp, const Derived, const OtherDerived > | binaryExpr (const Eigen::MatrixBase< OtherDerived > &other, const CustomBinaryOp &func=CustomBinaryOp()) const |
| Block< Derived > | block (Index startRow, Index startCol, Index blockRows, Index blockCols) |
| const Block< const Derived > | block (Index startRow, Index startCol, Index blockRows, Index blockCols) const |
| template<int BlockRows, int BlockCols> | |
| Block< Derived, BlockRows, BlockCols > | block (Index startRow, Index startCol) |
| template<int BlockRows, int BlockCols> | |
| const Block< const Derived, BlockRows, BlockCols > | block (Index startRow, Index startCol) const |
| template<int BlockRows, int BlockCols> | |
| Block< Derived, BlockRows, BlockCols > | block (Index startRow, Index startCol, Index blockRows, Index blockCols) |
| template<int BlockRows, int BlockCols> | |
| const Block< const Derived, BlockRows, BlockCols > | block (Index startRow, Index startCol, Index blockRows, Index blockCols) const |
| RealScalar | blueNorm () const |
| Block< Derived > | bottomLeftCorner (Index cRows, Index cCols) |
| const Block< const Derived > | bottomLeftCorner (Index cRows, Index cCols) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | bottomLeftCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | bottomLeftCorner () const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | bottomLeftCorner (Index cRows, Index cCols) |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | bottomLeftCorner (Index cRows, Index cCols) const |
| Block< Derived > | bottomRightCorner (Index cRows, Index cCols) |
| const Block< const Derived > | bottomRightCorner (Index cRows, Index cCols) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | bottomRightCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | bottomRightCorner () const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | bottomRightCorner (Index cRows, Index cCols) |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | bottomRightCorner (Index cRows, Index cCols) const |
| RowsBlockXpr | bottomRows (Index n) |
| ConstRowsBlockXpr | bottomRows (Index n) const |
| template<int N> | |
| NRowsBlockXpr< N >::Type | bottomRows (Index n=N) |
| template<int N> | |
| ConstNRowsBlockXpr< N >::Type | bottomRows (Index n=N) const |
| template<typename NewType > | |
| internal::cast_return_type < Derived, const CwiseUnaryOp < internal::scalar_cast_op < typename internal::traits < Derived >::Scalar, NewType > , const Derived > >::type | cast () const |
| ColXpr | col (Index i) |
| ConstColXpr | col (Index i) const |
| const ColPivHouseholderQR < PlainObject > | colPivHouseholderQr () const |
| ConstColwiseReturnType | colwise () const |
| ColwiseReturnType | colwise () |
| template<typename ResultType > | |
| void | computeInverseAndDetWithCheck (ResultType &inverse, typename ResultType::Scalar &determinant, bool &invertible, const RealScalar &absDeterminantThreshold=NumTraits< Scalar >::dummy_precision()) const |
| template<typename ResultType > | |
| void | computeInverseWithCheck (ResultType &inverse, bool &invertible, const RealScalar &absDeterminantThreshold=NumTraits< Scalar >::dummy_precision()) const |
| ConjugateReturnType | conjugate () const |
| Index | count () const |
| template<typename OtherDerived > | |
| MatrixBase< Derived > ::template cross_product_return_type < OtherDerived >::type | cross (const MatrixBase< OtherDerived > &other) const |
| template<typename OtherDerived > | |
| MatrixBase< Derived >::PlainObject | cross3 (const MatrixBase< OtherDerived > &other) const |
| const CwiseUnaryOp < internal::scalar_abs_op < Scalar >, const Derived > | cwiseAbs () const |
| const CwiseUnaryOp < internal::scalar_abs2_op < Scalar >, const Derived > | cwiseAbs2 () const |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < std::equal_to< Scalar > , const Derived, const OtherDerived > | cwiseEqual (const Eigen::MatrixBase< OtherDerived > &other) const |
| const CwiseScalarEqualReturnType | cwiseEqual (const Scalar &s) const |
| const CwiseUnaryOp < internal::scalar_inverse_op < Scalar >, const Derived > | cwiseInverse () const |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < internal::scalar_max_op < Scalar >, const Derived, const OtherDerived > | cwiseMax (const Eigen::MatrixBase< OtherDerived > &other) const |
| const CwiseBinaryOp < internal::scalar_max_op < Scalar >, const Derived, const ConstantReturnType > | cwiseMax (const Scalar &other) const |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < internal::scalar_min_op < Scalar >, const Derived, const OtherDerived > | cwiseMin (const Eigen::MatrixBase< OtherDerived > &other) const |
| const CwiseBinaryOp < internal::scalar_min_op < Scalar >, const Derived, const ConstantReturnType > | cwiseMin (const Scalar &other) const |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < std::not_equal_to< Scalar > , const Derived, const OtherDerived > | cwiseNotEqual (const Eigen::MatrixBase< OtherDerived > &other) const |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < internal::scalar_product_op < typename Derived::Scalar, typename OtherDerived::Scalar > , const Derived, const OtherDerived > | cwiseProduct (const Eigen::MatrixBase< OtherDerived > &other) const |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < internal::scalar_quotient_op < Scalar >, const Derived, const OtherDerived > | cwiseQuotient (const Eigen::MatrixBase< OtherDerived > &other) const |
| const CwiseUnaryOp < internal::scalar_sqrt_op < Scalar >, const Derived > | cwiseSqrt () const |
| Scalar | determinant () const |
| DiagonalReturnType | diagonal () |
| ConstDiagonalReturnType | diagonal () const |
| DiagonalDynamicIndexReturnType | diagonal (Index index) |
| ConstDiagonalDynamicIndexReturnType | diagonal (Index index) const |
| Index | diagonalSize () const |
| template<typename OtherDerived > | |
| internal::scalar_product_traits < typename internal::traits < Derived >::Scalar, typename internal::traits< OtherDerived > ::Scalar >::ReturnType | dot (const MatrixBase< OtherDerived > &other) const |
| EigenvaluesReturnType | eigenvalues () const |
| Computes the eigenvalues of a matrix. More... | |
| Matrix< Scalar, 3, 1 > | eulerAngles (Index a0, Index a1, Index a2) const |
| EvalReturnType | eval () const |
| void | fill (const Scalar &value) |
| template<unsigned int Added, unsigned int Removed> | |
| const Flagged< Derived, Added, Removed > | flagged () const |
| const ForceAlignedAccess< Derived > | forceAlignedAccess () const |
| ForceAlignedAccess< Derived > | forceAlignedAccess () |
| template<bool Enable> | |
| internal::add_const_on_value_type < typename internal::conditional< Enable, ForceAlignedAccess< Derived > , Derived & >::type >::type | forceAlignedAccessIf () const |
| template<bool Enable> | |
| internal::conditional< Enable, ForceAlignedAccess< Derived > , Derived & >::type | forceAlignedAccessIf () |
| const WithFormat< Derived > | format (const IOFormat &fmt) const |
| const FullPivHouseholderQR < PlainObject > | fullPivHouseholderQr () const |
| const FullPivLU< PlainObject > | fullPivLu () const |
| bool | hasNaN () const |
| SegmentReturnType | head (Index n) |
| ConstSegmentReturnType | head (Index n) const |
| template<int N> | |
| FixedSegmentReturnType< N >::Type | head (Index n=N) |
| template<int N> | |
| ConstFixedSegmentReturnType< N > ::Type | head (Index n=N) const |
| const HNormalizedReturnType | hnormalized () const |
| HomogeneousReturnType | homogeneous () const |
| const HouseholderQR< PlainObject > | householderQr () const |
| RealScalar | hypotNorm () const |
| const ImagReturnType | imag () const |
| NonConstImagReturnType | imag () |
| Index | innerSize () const |
| const internal::inverse_impl < Derived > | inverse () const |
| template<typename OtherDerived > | |
| bool | isApprox (const DenseBase< OtherDerived > &other, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isApproxToConstant (const Scalar &value, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isConstant (const Scalar &value, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isDiagonal (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isIdentity (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isLowerTriangular (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| template<typename Derived > | |
| bool | isMuchSmallerThan (const typename NumTraits< Scalar >::Real &other, const RealScalar &prec) const |
| template<typename OtherDerived > | |
| bool | isMuchSmallerThan (const DenseBase< OtherDerived > &other, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isOnes (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| template<typename OtherDerived > | |
| bool | isOrthogonal (const MatrixBase< OtherDerived > &other, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isUnitary (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isUpperTriangular (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isZero (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const |
| JacobiSVD< PlainObject > | jacobiSvd (unsigned int computationOptions=0) const |
| template<typename OtherDerived > | |
| const LazyProductReturnType < Derived, OtherDerived > ::Type | lazyProduct (const MatrixBase< OtherDerived > &other) const |
| const LDLT< PlainObject > | ldlt () const |
| ColsBlockXpr | leftCols (Index n) |
| ConstColsBlockXpr | leftCols (Index n) const |
| template<int N> | |
| NColsBlockXpr< N >::Type | leftCols (Index n=N) |
| template<int N> | |
| ConstNColsBlockXpr< N >::Type | leftCols (Index n=N) const |
| const LLT< PlainObject > | llt () const |
| template<int p> | |
| NumTraits< typename internal::traits< Derived > ::Scalar >::Real | lpNorm () const |
| const PartialPivLU< PlainObject > | lu () const |
| template<typename EssentialPart > | |
| void | makeHouseholder (EssentialPart &essential, Scalar &tau, RealScalar &beta) const |
| void | makeHouseholderInPlace (Scalar &tau, RealScalar &beta) |
| internal::traits< Derived >::Scalar | maxCoeff () const |
| template<typename IndexType > | |
| internal::traits< Derived >::Scalar | maxCoeff (IndexType *row, IndexType *col) const |
| template<typename IndexType > | |
| internal::traits< Derived >::Scalar | maxCoeff (IndexType *index) const |
| Scalar | mean () const |
| ColsBlockXpr | middleCols (Index startCol, Index numCols) |
| ConstColsBlockXpr | middleCols (Index startCol, Index numCols) const |
| template<int N> | |
| NColsBlockXpr< N >::Type | middleCols (Index startCol, Index n=N) |
| template<int N> | |
| ConstNColsBlockXpr< N >::Type | middleCols (Index startCol, Index n=N) const |
| RowsBlockXpr | middleRows (Index startRow, Index n) |
| ConstRowsBlockXpr | middleRows (Index startRow, Index n) const |
| template<int N> | |
| NRowsBlockXpr< N >::Type | middleRows (Index startRow, Index n=N) |
| template<int N> | |
| ConstNRowsBlockXpr< N >::Type | middleRows (Index startRow, Index n=N) const |
| internal::traits< Derived >::Scalar | minCoeff () const |
| template<typename IndexType > | |
| internal::traits< Derived >::Scalar | minCoeff (IndexType *row, IndexType *col) const |
| template<typename IndexType > | |
| internal::traits< Derived >::Scalar | minCoeff (IndexType *index) const |
| const NestByValue< Derived > | nestByValue () const |
| NoAlias< Derived, Eigen::MatrixBase > | noalias () |
| Index | nonZeros () const |
| RealScalar | norm () const |
| void | normalize () |
| const PlainObject | normalized () const |
| template<typename OtherDerived > | |
| bool | operator!= (const MatrixBase< OtherDerived > &other) const |
| const ScalarMultipleReturnType | operator* (const Scalar &scalar) const |
| const CwiseUnaryOp < internal::scalar_multiple2_op < Scalar, std::complex< Scalar > >, const Derived > | operator* (const std::complex< Scalar > &scalar) const |
| template<typename OtherDerived > | |
| const ProductReturnType < Derived, OtherDerived > ::Type | operator* (const MatrixBase< OtherDerived > &other) const |
| template<typename DiagonalDerived > | |
| const DiagonalProduct< Derived, DiagonalDerived, OnTheRight > | operator* (const DiagonalBase< DiagonalDerived > &diagonal) const |
| ScalarMultipleReturnType | operator* (const UniformScaling< Scalar > &s) const |
| template<typename OtherDerived > | |
| Derived & | operator*= (const EigenBase< OtherDerived > &other) |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < internal::scalar_sum_op < Scalar >, const Derived, const OtherDerived > | operator+ (const Eigen::MatrixBase< OtherDerived > &other) const |
| template<typename OtherDerived > | |
| Derived & | operator+= (const MatrixBase< OtherDerived > &other) |
| template<typename OtherDerived > | |
| const CwiseBinaryOp < internal::scalar_difference_op < Scalar >, const Derived, const OtherDerived > | operator- (const Eigen::MatrixBase< OtherDerived > &other) const |
| const CwiseUnaryOp < internal::scalar_opposite_op < typename internal::traits < Derived >::Scalar >, const Derived > | operator- () const |
| template<typename OtherDerived > | |
| Derived & | operator-= (const MatrixBase< OtherDerived > &other) |
| const CwiseUnaryOp < internal::scalar_quotient1_op < typename internal::traits < Derived >::Scalar >, const Derived > | operator/ (const Scalar &scalar) const |
| CommaInitializer< Derived > | operator<< (const Scalar &s) |
| template<typename OtherDerived > | |
| CommaInitializer< Derived > | operator<< (const DenseBase< OtherDerived > &other) |
| Derived & | operator= (const MatrixBase &other) |
| template<typename OtherDerived > | |
| bool | operator== (const MatrixBase< OtherDerived > &other) const |
| RealScalar | operatorNorm () const |
| Computes the L2 operator norm. More... | |
| Index | outerSize () const |
| const PartialPivLU< PlainObject > | partialPivLu () const |
| Scalar | prod () const |
| RealReturnType | real () const |
| NonConstRealReturnType | real () |
| template<typename Func > | |
| internal::result_of< Func(typename internal::traits< Derived > ::Scalar)>::type | redux (const Func &func) const |
| template<int RowFactor, int ColFactor> | |
| const Replicate< Derived, RowFactor, ColFactor > | replicate () const |
| const ReplicateReturnType | replicate (Index rowFacor, Index colFactor) const |
| void | resize (Index newSize) |
| void | resize (Index nbRows, Index nbCols) |
| ReverseReturnType | reverse () |
| ConstReverseReturnType | reverse () const |
| void | reverseInPlace () |
| ColsBlockXpr | rightCols (Index n) |
| ConstColsBlockXpr | rightCols (Index n) const |
| template<int N> | |
| NColsBlockXpr< N >::Type | rightCols (Index n=N) |
| template<int N> | |
| ConstNColsBlockXpr< N >::Type | rightCols (Index n=N) const |
| RowXpr | row (Index i) |
| ConstRowXpr | row (Index i) const |
| ConstRowwiseReturnType | rowwise () const |
| RowwiseReturnType | rowwise () |
| SegmentReturnType | segment (Index start, Index n) |
| ConstSegmentReturnType | segment (Index start, Index n) const |
| template<int N> | |
| FixedSegmentReturnType< N >::Type | segment (Index start, Index n=N) |
| template<int N> | |
| ConstFixedSegmentReturnType< N > ::Type | segment (Index start, Index n=N) const |
| template<typename ThenDerived , typename ElseDerived > | |
| const Select< Derived, ThenDerived, ElseDerived > | select (const DenseBase< ThenDerived > &thenMatrix, const DenseBase< ElseDerived > &elseMatrix) const |
| template<typename ThenDerived > | |
| const Select< Derived, ThenDerived, typename ThenDerived::ConstantReturnType > | select (const DenseBase< ThenDerived > &thenMatrix, const typename ThenDerived::Scalar &elseScalar) const |
| template<typename ElseDerived > | |
| const Select< Derived, typename ElseDerived::ConstantReturnType, ElseDerived > | select (const typename ElseDerived::Scalar &thenScalar, const DenseBase< ElseDerived > &elseMatrix) const |
| Derived & | setConstant (const Scalar &value) |
| Derived & | setIdentity () |
| Derived & | setIdentity (Index rows, Index cols) |
| Resizes to the given size, and writes the identity expression (not necessarily square) into *this. More... | |
| Derived & | setLinSpaced (Index size, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. More... | |
| Derived & | setLinSpaced (const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. More... | |
| Derived & | setOnes () |
| Derived & | setRandom () |
| Derived & | setZero () |
| RealScalar | squaredNorm () const |
| RealScalar | stableNorm () const |
| Scalar | sum () const |
| template<typename OtherDerived > | |
| void | swap (const DenseBase< OtherDerived > &other, int=OtherDerived::ThisConstantIsPrivateInPlainObjectBase) |
| template<typename OtherDerived > | |
| void | swap (PlainObjectBase< OtherDerived > &other) |
| SegmentReturnType | tail (Index n) |
| ConstSegmentReturnType | tail (Index n) const |
| template<int N> | |
| FixedSegmentReturnType< N >::Type | tail (Index n=N) |
| template<int N> | |
| ConstFixedSegmentReturnType< N > ::Type | tail (Index n=N) const |
| Block< Derived > | topLeftCorner (Index cRows, Index cCols) |
| const Block< const Derived > | topLeftCorner (Index cRows, Index cCols) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | topLeftCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | topLeftCorner () const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | topLeftCorner (Index cRows, Index cCols) |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | topLeftCorner (Index cRows, Index cCols) const |
| Block< Derived > | topRightCorner (Index cRows, Index cCols) |
| const Block< const Derived > | topRightCorner (Index cRows, Index cCols) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | topRightCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | topRightCorner () const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | topRightCorner (Index cRows, Index cCols) |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | topRightCorner (Index cRows, Index cCols) const |
| RowsBlockXpr | topRows (Index n) |
| ConstRowsBlockXpr | topRows (Index n) const |
| template<int N> | |
| NRowsBlockXpr< N >::Type | topRows (Index n=N) |
| template<int N> | |
| ConstNRowsBlockXpr< N >::Type | topRows (Index n=N) const |
| Scalar | trace () const |
| Eigen::Transpose< Derived > | transpose () |
| ConstTransposeReturnType | transpose () const |
| void | transposeInPlace () |
| template<unsigned int Mode> | |
| MatrixBase< Derived > ::template TriangularViewReturnType< Mode > ::Type | triangularView () |
| template<unsigned int Mode> | |
| MatrixBase< Derived > ::template ConstTriangularViewReturnType < Mode >::Type | triangularView () const |
| template<typename CustomUnaryOp > | |
| const CwiseUnaryOp < CustomUnaryOp, const Derived > | unaryExpr (const CustomUnaryOp &func=CustomUnaryOp()) const |
| Apply a unary operator coefficient-wise. More... | |
| template<typename CustomViewOp > | |
| const CwiseUnaryView < CustomViewOp, const Derived > | unaryViewExpr (const CustomViewOp &func=CustomViewOp()) const |
| PlainObject | unitOrthogonal (void) const |
| CoeffReturnType | value () const |
| template<typename Visitor > | |
| void | visit (Visitor &func) const |
Static Public Member Functions | |
| static const ConstantReturnType | Constant (Index rows, Index cols, const Scalar &value) |
| static const ConstantReturnType | Constant (Index size, const Scalar &value) |
| static const ConstantReturnType | Constant (const Scalar &value) |
| static const IdentityReturnType | Identity () |
| static const IdentityReturnType | Identity (Index rows, Index cols) |
| static const SequentialLinSpacedReturnType | LinSpaced (Sequential_t, Index size, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. More... | |
| static const RandomAccessLinSpacedReturnType | LinSpaced (Index size, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. More... | |
| static const SequentialLinSpacedReturnType | LinSpaced (Sequential_t, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. More... | |
| static const RandomAccessLinSpacedReturnType | LinSpaced (const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. More... | |
| template<typename CustomNullaryOp > | |
| static const CwiseNullaryOp < CustomNullaryOp, Derived > | NullaryExpr (Index rows, Index cols, const CustomNullaryOp &func) |
| template<typename CustomNullaryOp > | |
| static const CwiseNullaryOp < CustomNullaryOp, Derived > | NullaryExpr (Index size, const CustomNullaryOp &func) |
| template<typename CustomNullaryOp > | |
| static const CwiseNullaryOp < CustomNullaryOp, Derived > | NullaryExpr (const CustomNullaryOp &func) |
| static const ConstantReturnType | Ones (Index rows, Index cols) |
| static const ConstantReturnType | Ones (Index size) |
| static const ConstantReturnType | Ones () |
| static const CwiseNullaryOp < internal::scalar_random_op < Scalar >, Derived > | Random (Index rows, Index cols) |
| static const CwiseNullaryOp < internal::scalar_random_op < Scalar >, Derived > | Random (Index size) |
| static const CwiseNullaryOp < internal::scalar_random_op < Scalar >, Derived > | Random () |
| static const BasisReturnType | Unit (Index size, Index i) |
| static const BasisReturnType | Unit (Index i) |
| static const BasisReturnType | UnitW () |
| static const BasisReturnType | UnitX () |
| static const BasisReturnType | UnitY () |
| static const BasisReturnType | UnitZ () |
| static const ConstantReturnType | Zero (Index rows, Index cols) |
| static const ConstantReturnType | Zero (Index size) |
| static const ConstantReturnType | Zero () |
Related Functions | |
(Note that these are not member functions.) | |
| template<typename Derived > | |
| std::ostream & | operator<< (std::ostream &s, const DenseBase< Derived > &m) |
The type of indices.
To change this, #define the preprocessor symbol EIGEN_DEFAULT_DENSE_INDEX_TYPE.
| typedef Matrix<typename internal::traits<Derived>::Scalar, internal::traits<Derived>::RowsAtCompileTime, internal::traits<Derived>::ColsAtCompileTime, AutoAlign | (internal::traits<Derived>::Flags&RowMajorBit ? RowMajor : ColMajor), internal::traits<Derived>::MaxRowsAtCompileTime, internal::traits<Derived>::MaxColsAtCompileTime > PlainObject |
The plain matrix type corresponding to this expression.
This is not necessarily exactly the return type of eval(). In the case of plain matrices, the return type of eval() is a const reference to a matrix, not a matrix! It is however guaranteed that the return type of eval() is either PlainObject or const PlainObject&.
|
inherited |
| Enumerator | |
|---|---|
| RowsAtCompileTime |
The number of rows at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant.
|
| ColsAtCompileTime |
The number of columns at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant.
|
| SizeAtCompileTime |
This is equal to the number of coefficients, i.e. the number of rows times the number of columns, or to Dynamic if this is not known at compile-time.
|
| MaxRowsAtCompileTime |
This value is equal to the maximum possible number of rows that this expression might have. If this expression might have an arbitrarily high number of rows, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. |
| MaxColsAtCompileTime |
This value is equal to the maximum possible number of columns that this expression might have. If this expression might have an arbitrarily high number of columns, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. |
| MaxSizeAtCompileTime |
This value is equal to the maximum possible number of coefficients that this expression might have. If this expression might have an arbitrarily high number of coefficients, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. |
| IsVectorAtCompileTime |
This is set to true if either the number of rows or the number of columns is known at compile-time to be equal to 1. Indeed, in that case, we are dealing with a column-vector (if there is only one column) or with a row-vector (if there is only one row). |
| Flags |
This stores expression Flags flags which may or may not be inherited by new expressions constructed from this one. See the list of flags. |
| IsRowMajor |
True if this expression has row-major storage order. |
| CoeffReadCost |
This is a rough measure of how expensive it is to read one coefficient from this expression. |
|
inline |
Example:
Output:
Here is the 2x2 complex matrix m: (-0.211,0.68) (-0.605,0.823) (0.597,0.566) (0.536,-0.33) Here is the adjoint of m: (-0.211,-0.68) (0.597,-0.566) (-0.605,-0.823) (0.536,0.33)
|
inline |
This is the "in place" version of adjoint(): it replaces *this by its own transpose. Thus, doing
has the same effect on m as doing
and is faster and also safer because in the latter line of code, forgetting the eval() results in a bug caused by aliasing.
Notice however that this method is only useful if you want to replace a matrix by its own adjoint. If you just need the adjoint of a matrix, use adjoint().
*this must be a resizable matrix. This excludes (non-square) fixed-size matrices, block-expressions and maps.
|
inlineinherited |
Example:
Output:
Is ( 0.68 -0.211 0.566) inside the box: 0 Is (0.597 0.823 0.605) inside the box: 1
References Eigen::Dynamic.
|
inlineinherited |
*this contains only finite numbers, i.e., no NaN and no +/-INF values.
|
inlineinherited |
| void applyHouseholderOnTheLeft | ( | const EssentialPart & | essential, |
| const Scalar & | tau, | ||
| Scalar * | workspace | ||
| ) |
Apply the elementary reflector H given by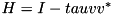 
with ![$ v^T = [1 essential^T] $](form_131.png)
from the left to a vector or matrix.
On input:
| essential | the essential part of the vector v |
| tau | the scaling factor of the Householder transformation |
| workspace | a pointer to working space with at least this->cols() * essential.size() entries |
| void applyHouseholderOnTheRight | ( | const EssentialPart & | essential, |
| const Scalar & | tau, | ||
| Scalar * | workspace | ||
| ) |
Apply the elementary reflector H given by 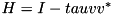with from the right to a vector or matrix.
On input:
| essential | the essential part of the vector v |
| tau | the scaling factor of the Householder transformation |
| workspace | a pointer to working space with at least this->cols() * essential.size() entries |
|
inline |
replaces *this by other * *this.
Example:
Output:
At start, A = 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 After applyOnTheLeft, A = -0.211 0.823 0.536 0.566 -0.605 -0.444 0.68 0.597 -0.33
References EigenBase< Derived >::derived().
|
inline |
This is defined in the Jacobi module.
Applies the rotation in the plane j to the rows p and q of *this, i.e., it computes B = J * B, with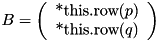 
.
|
inline |
replaces *this by *this * other. It is equivalent to MatrixBase::operator*=().
Example:
Output:
At start, A = 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 After A *= B, A = -0.33 0.68 0.597 0.536 -0.211 0.823 -0.444 0.566 -0.605 After applyOnTheRight, A = 0.597 -0.33 0.68 0.823 0.536 -0.211 -0.605 -0.444 0.566
References EigenBase< Derived >::derived().
|
inline |
|
inline |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
2 0 0 0 5 0 0 0 6
Referenced by Transform< Scalar, Dim, Mode, _Options >::fromPositionOrientationScale(), Transform< Scalar, Dim, Mode, _Options >::prescale(), and Transform< Scalar, Dim, Mode, _Options >::scale().
|
inline |
The template parameter CustomBinaryOp is the type of the functor of the custom operator (see class CwiseBinaryOp for an example)
Here is an example illustrating the use of custom functors:
Output:
(0.68,0.271) (0.823,-0.967) (-0.444,-0.687) (-0.27,0.998) (-0.211,0.435) (-0.605,-0.514) (0.108,-0.198) (0.0268,-0.563) (0.566,-0.717) (-0.33,-0.726) (-0.0452,-0.74) (0.904,0.0259) (0.597,0.214) (0.536,0.608) (0.258,-0.782) (0.832,0.678)
|
inlineinherited |
| startRow | the first row in the block |
| startCol | the first column in the block |
| blockRows | the number of rows in the block |
| blockCols | the number of columns in the block |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.block(1, 1, 2, 2): -6 1 -3 0 Now the matrix m is: 7 9 -5 -3 -2 0 0 0 6 0 0 9 6 6 3 9
|
inlineinherited |
This is the const version of block(Index,Index,Index,Index).
The template parameters BlockRows and BlockCols are the number of rows and columns in the block.
| startRow | the first row in the block |
| startCol | the first column in the block |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.block<2,2>(1,1): -6 1 -3 0 Now the matrix m is: 7 9 -5 -3 -2 0 0 0 6 0 0 9 6 6 3 9
|
inlineinherited |
This is the const version of block<>(Index, Index).
|
inlineinherited |
| BlockRows | number of rows in block as specified at compile-time |
| BlockCols | number of columns in block as specified at compile-time |
| startRow | the first row in the block |
| startCol | the first column in the block |
| blockRows | number of rows in block as specified at run-time |
| blockCols | number of columns in block as specified at run-time |
This function is mainly useful for blocks where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, blockRows should equal BlockRows unless BlockRows is Dynamic, and the same for the number of columns.
Example:
Output:
Matrix4i m = Matrix4i::Random(); cout << "Here is the matrix m:" << endl << m << endl; cout << "Here is the block:" << endl << m.block<2, Dynamic>(1, 1, 2, 3) << endl; m.block<2, Dynamic>(1, 1, 2, 3).setZero(); cout << "Now the matrix m is:" << endl << m << endl;
|
inlineinherited |
This is the const version of block<>(Index, Index, Index, Index).
|
inline |
*this using the Blue's algorithm. A Portable Fortran Program to Find the Euclidean Norm of a Vector, ACM TOMS, Vol 4, Issue 1, 1978.For architecture/scalar types without vectorization, this version is much faster than stableNorm(). Otherwise the stableNorm() is faster.
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomLeftCorner(2, 2): 6 -3 6 6 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 0 0 0 9 0 0 3 9
This is the const version of bottomLeftCorner(Index, Index).
|
inlineinherited |
The template parameters CRows and CCols are the number of rows and columns in the corner.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomLeftCorner<2,2>(): 6 -3 6 6 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 0 0 0 9 0 0 3 9
|
inlineinherited |
This is the const version of bottomLeftCorner<int, int>().
| CRows | number of rows in corner as specified at compile-time |
| CCols | number of columns in corner as specified at compile-time |
| cRows | number of rows in corner as specified at run-time |
| cCols | number of columns in corner as specified at run-time |
This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomLeftCorner<2,Dynamic>(2,2): 6 -3 6 6 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 0 0 0 9 0 0 3 9
|
inlineinherited |
This is the const version of bottomLeftCorner<int, int>(Index, Index).
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomRightCorner(2, 2): 0 9 3 9 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 6 -3 0 0 6 6 0 0
This is the const version of bottomRightCorner(Index, Index).
|
inlineinherited |
The template parameters CRows and CCols are the number of rows and columns in the corner.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomRightCorner<2,2>(): 0 9 3 9 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 6 -3 0 0 6 6 0 0
|
inlineinherited |
This is the const version of bottomRightCorner<int, int>().
| CRows | number of rows in corner as specified at compile-time |
| CCols | number of columns in corner as specified at compile-time |
| cRows | number of rows in corner as specified at run-time |
| cCols | number of columns in corner as specified at run-time |
This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomRightCorner<2,Dynamic>(2,2): 0 9 3 9 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 6 -3 0 0 6 6 0 0
|
inlineinherited |
This is the const version of bottomRightCorner<int, int>(Index, Index).
|
inlineinherited |
| n | the number of rows in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.bottomRows(2): 6 -3 0 9 6 6 3 9 Now the array a is: 7 9 -5 -3 -2 -6 1 0 0 0 0 0 0 0 0 0
|
inlineinherited |
This is the const version of bottomRows(Index).
|
inlineinherited |
| N | the number of rows in the block as specified at compile-time |
| n | the number of rows in the block as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.bottomRows<2>(): 6 -3 0 9 6 6 3 9 Now the array a is: 7 9 -5 -3 -2 -6 1 0 0 0 0 0 0 0 0 0
|
inlineinherited |
This is the const version of bottomRows<int>().
|
inline |
The template parameter NewScalar is the type we are casting the scalars to.
|
inlineinherited |
Example:
Output:
1 4 0 0 5 0 0 6 1
Referenced by VectorwiseOp< ExpressionType, Direction >::cross().
| const ColPivHouseholderQR< typename MatrixBase< Derived >::PlainObject > colPivHouseholderQr | ( | ) | const |
*this.
|
inlineinherited |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Here is the sum of each column: 1.04 0.815 -0.238 Here is the maximum absolute value of each column: 0.68 0.823 0.536
Referenced by Eigen::umeyama().
|
inlineinherited |
|
inline |
This is defined in the LU module.
Computation of matrix inverse and determinant, with invertibility check.
This is only for fixed-size square matrices of size up to 4x4.
| inverse | Reference to the matrix in which to store the inverse. |
| determinant | Reference to the variable in which to store the determinant. |
| invertible | Reference to the bool variable in which to store whether the matrix is invertible. |
| absDeterminantThreshold | Optional parameter controlling the invertibility check. The matrix will be declared invertible if the absolute value of its determinant is greater than this threshold. |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Its determinant is 0.209 It is invertible, and its inverse is: -0.199 2.23 2.84 1.01 -0.555 -1.42 -1.62 3.59 3.29
|
inline |
This is defined in the LU module.
Computation of matrix inverse, with invertibility check.
This is only for fixed-size square matrices of size up to 4x4.
| inverse | Reference to the matrix in which to store the inverse. |
| invertible | Reference to the bool variable in which to store whether the matrix is invertible. |
| absDeterminantThreshold | Optional parameter controlling the invertibility check. The matrix will be declared invertible if the absolute value of its determinant is greater than this threshold. |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 It is invertible, and its inverse is: -0.199 2.23 2.84 1.01 -0.555 -1.42 -1.62 3.59 3.29
|
inline |
*this.
|
inlinestaticinherited |
The parameters nbRows and nbCols are the number of rows and of columns of the returned matrix. Must be compatible with this DenseBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass nbRows and nbCols as arguments, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
References DenseBase< Derived >::NullaryExpr().
|
inlinestaticinherited |
The parameter size is the size of the returned vector. Must be compatible with this DenseBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
References DenseBase< Derived >::NullaryExpr().
|
inlinestaticinherited |
This variant is only for fixed-size DenseBase types. For dynamic-size types, you need to use the variants taking size arguments.
The template parameter CustomNullaryOp is the type of the functor.
References DenseBase< Derived >::NullaryExpr().
|
inline |
This is defined in the Geometry module.
*this and other Here is a very good explanation of cross-product: http://xkcd.com/199/
|
inline |
This is defined in the Geometry module.
*this and other using only the x, y, and z coefficientsThe size of *this and other must be four. This function is especially useful when using 4D vectors instead of 3D ones to get advantage of SSE/AltiVec vectorization.
|
inline |
*this Example:
Output:
2 4 6 5 1 0
|
inline |
*this Example:
Output:
4 16 36 25 1 0
|
inline |
Example:
Output:
Comparing m with identity matrix: 1 1 0 1 Number of coefficients that are equal: 3
Referenced by MatrixBase< DiagonalProduct< MatrixType, DiagonalType, ProductOrder > >::operator==().
|
inline |
*this and a scalar s
|
inline |
Example:
Output:
0.5 2 1 0.333 4 1
|
inline |
Example:
Output:
4 3 4
|
inline |
|
inline |
Example:
Output:
2 2 3
|
inline |
|
inline |
Example:
Output:
Comparing m with identity matrix: 0 0 1 0 Number of coefficients that are not equal: 1
Referenced by MatrixBase< DiagonalProduct< MatrixType, DiagonalType, ProductOrder > >::operator!=().
|
inline |
Example:
Output:
a: 7 6 -3 -2 9 6 6 -6 -5 b: 1 -3 9 0 0 3 3 9 5 c: 7 -18 -27 0 0 18 18 -54 -25
|
inline |
Example:
Output:
0.5 1.5 1.33
|
inline |
Example:
Output:
1 1.41 2
|
inline |
This is defined in the LU module.
|
inline |
*this *this is not required to be square.
Example:
Output:
Here is the matrix m: 7 6 -3 -2 9 6 6 -6 -5 Here are the coefficients on the main diagonal of m: 7 9 -5
*this *this is not required to be square.
The template parameter DiagIndex represent a super diagonal if DiagIndex > 0 and a sub diagonal otherwise. DiagIndex == 0 is equivalent to the main diagonal.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here are the coefficients on the 1st super-diagonal and 2nd sub-diagonal of m: 9 1 9 6 6
Referenced by AngleAxis< Scalar >::toRotationMatrix().
|
inline |
This is the const version of diagonal().
This is the const version of diagonal<int>().
|
inline |
*this *this is not required to be square.
The template parameter DiagIndex represent a super diagonal if DiagIndex > 0 and a sub diagonal otherwise. DiagIndex == 0 is equivalent to the main diagonal.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here are the coefficients on the 1st super-diagonal and 2nd sub-diagonal of m: 9 1 9 6 6
|
inline |
This is the const version of diagonal(Index).
|
inline |
| internal::scalar_product_traits< typename internal::traits< Derived >::Scalar, typename internal::traits< OtherDerived >::Scalar >::ReturnType dot | ( | const MatrixBase< OtherDerived > & | other | ) | const |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inline |
Computes the eigenvalues of a matrix.
This is defined in the Eigenvalues module.
This function computes the eigenvalues with the help of the EigenSolver class (for real matrices) or the ComplexEigenSolver class (for complex matrices).
The eigenvalues are repeated according to their algebraic multiplicity, so there are as many eigenvalues as rows in the matrix.
The SelfAdjointView class provides a better algorithm for selfadjoint matrices.
Example:
Output:
The eigenvalues of the 3x3 matrix of ones are:
(-5.31e-17,0)
(3,0)
(0,0)
|
inlineinherited |
Notice that in the case of a plain matrix or vector (not an expression) this function just returns a const reference, in order to avoid a useless copy.
|
inlineinherited |
Alias for setConstant(): sets all coefficients in this expression to val.
Referenced by PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::determinant().
|
inlineinherited |
This is mostly for internal use.
|
inline |
|
inline |
|
inline |
|
inline |
|
inlineinherited |
See class IOFormat for some examples.
| const FullPivHouseholderQR< typename MatrixBase< Derived >::PlainObject > fullPivHouseholderQr | ( | ) | const |
*this.
|
inline |
This is defined in the LU module.
*this.
|
inlineinherited |
*this contains at least one Not A Number (NaN).
|
inlineinherited |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| n | the number of coefficients in the segment |
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.head(2): 7 -2 Now the vector v is: 0 0 6 6
|
inlineinherited |
This is the const version of head(Index).
|
inlineinherited |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| N | the number of coefficients in the segment as specified at compile-time |
| n | the number of coefficients in the segment as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.head(2): 7 -2 Now the vector v is: 0 0 6 6
|
inlineinherited |
This is the const version of head<int>().
|
inline |
This is defined in the Geometry module.
*this Example:
Output:
|
inline |
This is defined in the Geometry module.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
| const HouseholderQR< typename MatrixBase< Derived >::PlainObject > householderQr | ( | ) | const |
*this.
|
inline |
*this avoiding undeflow and overflow. This version use a concatenation of hypot() calls, and it is very slow.
|
inlinestatic |
This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variant taking size arguments.
Example:
Output:
1 0 0 0 0 1 0 0 0 0 1 0
References DenseBase< Derived >::NullaryExpr().
|
inlinestatic |
The parameters nbRows and nbCols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Identity() should be used instead.
Example:
Output:
1 0 0 0 1 0 0 0 1 0 0 0
References DenseBase< Derived >::NullaryExpr().
|
inline |
*this.
|
inline |
*this.
|
inlineinherited |
References DenseBase< Derived >::IsRowMajor, and DenseBase< Derived >::IsVectorAtCompileTime.
|
inline |
This is defined in the LU module.
For small fixed sizes up to 4x4, this method uses cofactors. In the general case, this method uses class PartialPivLU.
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Its inverse is: -0.199 2.23 2.84 1.01 -0.555 -1.42 -1.62 3.59 3.29
Referenced by Hyperplane< _Scalar, _AmbientDim, Options >::transform().
|
inherited |
true if *this is approximately equal to other, within the precision determined by prec.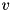
and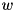 
are considered to be approximately equal within precision 
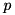if
![\[ \Vert v - w \Vert \leqslant p\,\min(\Vert v\Vert, \Vert w\Vert). \]](form_16.png)
*this is approximately equal to the zero matrix or vector. Indeed, isApprox(zero) returns false unless *this itself is exactly the zero matrix or vector. If you want to test whether *this is zero, use internal::isMuchSmallerThan(const RealScalar&, RealScalar) instead.Referenced by Transform< Scalar, Dim, Mode, _Options >::isApprox().
|
inherited |
|
inherited |
This is just an alias for isApproxToConstant().
| bool isDiagonal | ( | const RealScalar & | prec = NumTraits<Scalar>::dummy_precision() | ) | const |
Example:
Output:
Here's the matrix m:
1e+04 0 1
0 1e+04 0
0 0 1e+04
m.isDiagonal() returns: 0
m.isDiagonal(1e-3) returns: 1
| bool isIdentity | ( | const RealScalar & | prec = NumTraits<Scalar>::dummy_precision() | ) | const |
Example:
Output:
Here's the matrix m:
1 0 0.0001
0 1 0
0 0 1
m.isIdentity() returns: 0
m.isIdentity(1e-3) returns: 1
| bool isLowerTriangular | ( | const RealScalar & | prec = NumTraits<Scalar>::dummy_precision() | ) | const |
|
inherited |
true if the norm of *this is much smaller than other, within the precision determined by prec.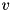 is considered to be much smaller than 
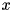within precision 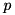if
![\[ \Vert v \Vert \leqslant p\,\vert x\vert. \]](form_18.png)
For matrices, the comparison is done using the Hilbert-Schmidt norm. For this reason, the value of the reference scalar other should come from the Hilbert-Schmidt norm of a reference matrix of same dimensions.
|
inherited |
true if the norm of *this is much smaller than the norm of other, within the precision determined by prec.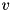 is considered to be much smaller than a vector 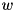within precision 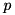if
![\[ \Vert v \Vert \leqslant p\,\Vert w\Vert. \]](form_19.png)
|
inherited |
Example:
Output:
Here's the matrix m: 1 1 1 1 1 1 1 1 1 m.isOnes() returns: 0 m.isOnes(1e-3) returns: 1
| bool isOrthogonal | ( | const MatrixBase< OtherDerived > & | other, |
| const RealScalar & | prec = NumTraits<Scalar>::dummy_precision() |
||
| ) | const |
Example:
Output:
Here's the vector v:
1
0
0
Here's the vector w:
0.0001
0
1
v.isOrthogonal(w) returns: 0
v.isOrthogonal(w,1e-3) returns: 1
| bool isUnitary | ( | const RealScalar & | prec = NumTraits<Scalar>::dummy_precision() | ) | const |
m.isUnitary() returns true if and only if the columns (equivalently, the rows) of m form an orthonormal basis.Example:
Output:
Here's the matrix m:
1 0 0.0001
0 1 0
0 0 1
m.isUnitary() returns: 0
m.isUnitary(1e-3) returns: 1
| bool isUpperTriangular | ( | const RealScalar & | prec = NumTraits<Scalar>::dummy_precision() | ) | const |
|
inherited |
Example:
Output:
Here's the matrix m:
0 0 0.0001
0 0 0
0 0 0
m.isZero() returns: 0
m.isZero(1e-3) returns: 1
| JacobiSVD< typename MatrixBase< Derived >::PlainObject > jacobiSvd | ( | unsigned int | computationOptions = 0 | ) | const |
This is defined in the SVD module.
*this computed by two-sided Jacobi transformations.| const LazyProductReturnType< Derived, OtherDerived >::Type lazyProduct | ( | const MatrixBase< OtherDerived > & | other | ) | const |
*this and other without implicit evaluation.The returned product will behave like any other expressions: the coefficients of the product will be computed once at a time as requested. This might be useful in some extremely rare cases when only a small and no coherent fraction of the result's coefficients have to be computed.
References Eigen::Dynamic.
|
inline |
This is defined in the Cholesky module.
*this
|
inlineinherited |
| n | the number of columns in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.leftCols(2): 7 9 -2 -6 6 -3 6 6 Now the array a is: 0 0 -5 -3 0 0 1 0 0 0 0 9 0 0 3 9
|
inlineinherited |
This is the const version of leftCols(Index).
|
inlineinherited |
| N | the number of columns in the block as specified at compile-time |
| n | the number of columns in the block as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.leftCols<2>(): 7 9 -2 -6 6 -3 6 6 Now the array a is: 0 0 -5 -3 0 0 1 0 0 0 0 9 0 0 3 9
|
inlineinherited |
This is the const version of leftCols<int>().
|
inlinestaticinherited |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. This particular version of LinSpaced() uses sequential access, i.e. vector access is assumed to be a(0), a(1), ..., a(size). This assumption allows for better vectorization and yields faster code than the random access version.
When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
References DenseBase< Derived >::NullaryExpr().
|
inlinestaticinherited |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
References DenseBase< Derived >::NullaryExpr().
|
inlinestaticinherited |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. This particular version of LinSpaced() uses sequential access, i.e. vector access is assumed to be a(0), a(1), ..., a(size). This assumption allows for better vectorization and yields faster code than the random access version.
When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
References DenseBase< Derived >::NullaryExpr().
|
inlinestaticinherited |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
References DenseBase< Derived >::NullaryExpr().
|
inline |
This is defined in the Cholesky module.
*this
|
inline |
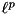norm of *this, that is, returns the p-th root of the sum of the p-th powers of the absolute values of the coefficients of *this. If p is the special value Eigen::Infinity, this function returns the 
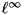norm, that is the maximum of the absolute values of the coefficients of *this.
|
inline |
This is defined in the LU module.
Synonym of partialPivLu().
*this.| void makeHouseholder | ( | EssentialPart & | essential, |
| Scalar & | tau, | ||
| RealScalar & | beta | ||
| ) | const |
Computes the elementary reflector H such that: ![$ H *this = [ beta 0 ... 0]^T $](form_129.png)
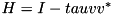where the transformation H is: and the vector v is:
On output:
| essential | the essential part of the vector v |
| tau | the scaling factor of the Householder transformation |
| beta | the result of H * *this |
| void makeHouseholderInPlace | ( | Scalar & | tau, |
| RealScalar & | beta | ||
| ) |
Computes the elementary reflector H such that: where the transformation H is: 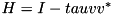and the vector v is:
The essential part of the vector v is stored in *this.
On output:
| tau | the scaling factor of the Householder transformation |
| beta | the result of H * *this |
|
inlineinherited |
*this. *this contains NaN.
|
inherited |
*this contains NaN.
|
inherited |
*this contains NaN.
|
inlineinherited |
| startCol | the index of the first column in the block |
| numCols | the number of columns in the block |
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(1..3,:) = -6 0 9 -3 3 3 6 -3 5 -5 0 -8 1 9 2
This is the const version of middleCols(Index,Index).
| N | the number of columns in the block as specified at compile-time |
| startCol | the index of the first column in the block |
| n | the number of columns in the block as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(:,1..3) = -6 0 9 -3 3 3 6 -3 5 -5 0 -8 1 9 2
This is the const version of middleCols<int>().
| startRow | the index of the first row in the block |
| n | the number of rows in the block |
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(2..3,:) = 6 6 -3 5 -8 6 -5 0 -8 6
This is the const version of middleRows(Index,Index).
| N | the number of rows in the block as specified at compile-time |
| startRow | the index of the first row in the block |
| n | the number of rows in the block as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(1..3,:) = -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6
This is the const version of middleRows<int>().
|
inlineinherited |
*this. *this contains NaN.
|
inherited |
*this contains NaN.
|
inherited |
*this contains NaN.
|
inlineinherited |
| NoAlias< Derived, MatrixBase > noalias | ( | ) |
*this with an operator= assuming no aliasing between *this and the source expression.More precisely, noalias() allows to bypass the EvalBeforeAssignBit flag. Currently, even though several expressions may alias, only product expressions have this flag. Therefore, noalias() is only usefull when the source expression contains a matrix product.
Here are some examples where noalias is usefull:
On the other hand the following example will lead to a wrong result:
because the result matrix A is also an operand of the matrix product. Therefore, there is no alternative than evaluating A * B in a temporary, that is the default behavior when you write:
|
inlineinherited |
|
inline |
*this, and for matrices the Frobenius norm. In both cases, it consists in the square root of the sum of the square of all the matrix entries. For vectors, this is also equals to the square root of the dot product of *this with itself.
|
inline |
Normalizes the vector, i.e. divides it by its own norm.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inline |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Referenced by QuaternionBase< Derived >::setFromTwoVectors().
|
inlinestaticinherited |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
Referenced by DenseBase< Derived >::Constant(), MatrixBase< Derived >::Identity(), and DenseBase< Derived >::LinSpaced().
|
inlinestaticinherited |
The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
|
inlinestaticinherited |
This variant is only for fixed-size DenseBase types. For dynamic-size types, you need to use the variants taking size arguments.
The template parameter CustomNullaryOp is the type of the functor.
|
inlinestaticinherited |
The parameters nbRows and nbCols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Ones() should be used instead.
Example:
Output:
1 1 1 1 1 1
The parameter newSize is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Ones() should be used instead.
Example:
Output:
6 6 6 6 1 1
|
inlinestaticinherited |
This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.
Example:
Output:
1 1 1 1 6 6 6 6
|
inline |
*this and other are not exactly equal to each other.
|
inline |
*this scaled by the scalar factor scalar
|
inline |
Overloaded for efficient real matrix times complex scalar value
|
inline |
*this and other.References Eigen::Dynamic.
|
inline |
*this by the diagonal matrix diagonal. | MatrixBase< Derived >::ScalarMultipleReturnType operator* | ( | const UniformScaling< Scalar > & | s | ) | const |
Concatenates a linear transformation matrix and a uniform scaling
|
inline |
replaces *this by *this * other.
*this Example:
Output:
At start, A = 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 After A *= B, A = -0.33 0.68 0.597 0.536 -0.211 0.823 -0.444 0.566 -0.605 After applyOnTheRight, A = 0.597 -0.33 0.68 0.823 0.536 -0.211 -0.605 -0.444 0.566
References EigenBase< Derived >::derived().
| const CwiseBinaryOp< internal::scalar_sum_op <Scalar>, const Derived, const OtherDerived> operator+ | ( | const Eigen::MatrixBase< OtherDerived > & | other | ) | const |
*this and other
|
inline |
replaces *this by *this + other.
*this | const CwiseBinaryOp< internal::scalar_difference_op <Scalar>, const Derived, const OtherDerived> operator- | ( | const Eigen::MatrixBase< OtherDerived > & | other | ) | const |
*this and other
|
inline |
*this
|
inline |
replaces *this by *this - other.
*this
|
inline |
*this divided by the scalar value scalar
|
inlineinherited |
Convenient operator to set the coefficients of a matrix.
The coefficients must be provided in a row major order and exactly match the size of the matrix. Otherwise an assertion is raised.
Example:
Output:
1 2 3 4 5 6 7 8 9 10 11 0 12 13 0 0 0 1 14 15 16 14 5 6 15 8 9
|
inlineinherited |
|
inline |
Special case of the template operator=, in order to prevent the compiler from generating a default operator= (issue hit with g++ 4.1)
|
inline |
*this and other are all exactly equal.
|
inline |
Computes the L2 operator norm.
This is defined in the Eigenvalues module.
This function computes the L2 operator norm of a matrix, which is also known as the spectral norm. The norm of a matrix 
is defined to be
![\[ \|A\|_2 = \max_x \frac{\|Ax\|_2}{\|x\|_2} \]](form_87.png)
where the maximum is over all vectors and the norm on the right is the Euclidean vector norm. The norm equals the largest singular value, which is the square root of the largest eigenvalue of the positive semi-definite matrix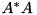 
.
The current implementation uses the eigenvalues of 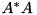, as computed by SelfAdjointView::eigenvalues(), to compute the operator norm of a matrix. The SelfAdjointView class provides a better algorithm for selfadjoint matrices.
Example:
Output:
The operator norm of the 3x3 matrix of ones is 3
|
inlineinherited |
References DenseBase< Derived >::IsRowMajor, and DenseBase< Derived >::IsVectorAtCompileTime.
|
inline |
This is defined in the LU module.
*this.
|
inlineinherited |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Here is the product of all the coefficients: 0.0019
References Eigen::Dynamic.
|
inlinestaticinherited |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Random() should be used instead.
Example:
Output:
7 6 9 -2 6 -6
This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary matrix whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.
|
inlinestaticinherited |
The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Random() should be used instead.
Example:
Output:
7 -2
This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary vector whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.
|
inlinestaticinherited |
This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.
Example:
Output:
700 600 -200 600
This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary matrix whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.
|
inline |
*this.
|
inline |
*this.
|
inlineinherited |
The template parameter BinaryOp is the type of the functor func which must be an associative operator. Both current STL and TR1 functor styles are handled.
|
inlineinherited |
*this Example:
Output:
Here is the matrix m: 7 6 9 -2 6 -6 m.replicate<3,2>() = ... 7 6 9 7 6 9 -2 6 -6 -2 6 -6 7 6 9 7 6 9 -2 6 -6 -2 6 -6 7 6 9 7 6 9 -2 6 -6 -2 6 -6
|
inlineinherited |
*this Example:
Output:
Here is the vector v: 7 -2 6 v.replicate(2,5) = ... 7 7 7 7 7 -2 -2 -2 -2 -2 6 6 6 6 6 7 7 7 7 7 -2 -2 -2 -2 -2 6 6 6 6 6
|
inlineinherited |
Only plain matrices/arrays, not expressions, may be resized; therefore the only useful resize methods are Matrix::resize() and Array::resize(). The present method only asserts that the new size equals the old size, and does nothing else.
Only plain matrices/arrays, not expressions, may be resized; therefore the only useful resize methods are Matrix::resize() and Array::resize(). The present method only asserts that the new size equals the old size, and does nothing else.
|
inlineinherited |
Example:
Output:
Here is the matrix m: 7 6 -3 1 -2 9 6 0 6 -6 -5 3 Here is the reverse of m: 3 -5 -6 6 0 6 9 -2 1 -3 6 7 Here is the coefficient (1,0) in the reverse of m: 0 Let us overwrite this coefficient with the value 4. Now the matrix m is: 7 6 -3 1 -2 9 6 4 6 -6 -5 3
|
inlineinherited |
This is the const version of reverse().
|
inlineinherited |
This is the "in place" version of reverse: it reverses *this.
In most cases it is probably better to simply use the reversed expression of a matrix. However, when reversing the matrix data itself is really needed, then this "in-place" version is probably the right choice because it provides the following additional features:
|
inlineinherited |
| n | the number of columns in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.rightCols(2): -5 -3 1 0 0 9 3 9 Now the array a is: 7 9 0 0 -2 -6 0 0 6 -3 0 0 6 6 0 0
|
inlineinherited |
This is the const version of rightCols(Index).
|
inlineinherited |
| N | the number of columns in the block as specified at compile-time |
| n | the number of columns in the block as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.rightCols<2>(): -5 -3 1 0 0 9 3 9 Now the array a is: 7 9 0 0 -2 -6 0 0 6 -3 0 0 6 6 0 0
|
inlineinherited |
This is the const version of rightCols<int>().
|
inlineinherited |
Example:
Output:
1 0 0 4 5 6 0 0 1
Referenced by VectorwiseOp< ExpressionType, Direction >::cross(), and Transform< Scalar, Dim, Mode, _Options >::pretranslate().
|
inlineinherited |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Here is the sum of each row: 0.948 1.15 -0.483 Here is the maximum absolute value of each row: 0.68 0.823 0.605
Referenced by Eigen::umeyama().
|
inlineinherited |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| start | the first coefficient in the segment |
| n | the number of coefficients in the segment |
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.segment(1, 2): -2 6 Now the vector v is: 7 0 0 6
This is the const version of segment(Index,Index).
*this This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| N | the number of coefficients in the segment as specified at compile-time |
| start | the index of the first element in the segment |
| n | the number of coefficients in the segment as specified at compile-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.segment<2>(1): -2 6 Now the vector v is: 7 -2 0 0
This is the const version of segment<int>(Index).
|
inlineinherited |
Version of DenseBase::select(const DenseBase&, const DenseBase&) with the else expression being a scalar value.
|
inlineinherited |
Version of DenseBase::select(const DenseBase&, const DenseBase&) with the then expression being a scalar value.
|
inlineinherited |
Sets all coefficients in this expression to value.
|
inline |
Writes the identity expression (not necessarily square) into *this.
Example:
Output:
0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0
Referenced by Transform< Scalar, Dim, Mode, _Options >::setIdentity().
Resizes to the given size, and writes the identity expression (not necessarily square) into *this.
| nbRows | the new number of rows |
| nbCols | the new number of columns |
Example:
Output:
1 0 0 0 1 0 0 0 1
|
inlineinherited |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
0.5 0.75 1 1.25 1.5
|
inlineinherited |
Sets a linearly space vector.
The function fill *this with equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inlineinherited |
Sets all coefficients in this expression to one.
Example:
Output:
7 9 -5 -3 1 1 1 1 6 -3 0 9 6 6 3 9
|
inlineinherited |
Sets all coefficients in this expression to random values.
Example:
Output:
0 7 0 0 0 -2 0 0 0 6 0 0 0 6 0 0
|
inlineinherited |
Sets all coefficients in this expression to zero.
Example:
Output:
7 9 -5 -3 0 0 0 0 6 -3 0 9 6 6 3 9
|
inline |
|
inline |
*this avoiding underflow and overflow. This version use a blockwise two passes algorithm: 1 - find the absolute largest coefficient s 2 - compute 
in a standard wayFor architecture/scalar types supporting vectorization, this version is faster than blueNorm(). Otherwise the blueNorm() is much faster.
References Eigen::AlignedBit, and Eigen::DirectAccessBit.
|
inlineinherited |
References Eigen::Dynamic.
|
inlineinherited |
swaps *this with the expression other.
|
inlineinherited |
swaps *this with the matrix or array other.
|
inlineinherited |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| n | the number of coefficients in the segment |
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.tail(2): 6 6 Now the vector v is: 7 -2 0 0
|
inlineinherited |
This is the const version of tail(Index).
|
inlineinherited |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| N | the number of coefficients in the segment as specified at compile-time |
| n | the number of coefficients in the segment as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.tail(2): 6 6 Now the vector v is: 7 -2 0 0
|
inlineinherited |
This is the const version of tail<int>.
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topLeftCorner(2, 2): 7 9 -2 -6 Now the matrix m is: 0 0 -5 -3 0 0 1 0 6 -3 0 9 6 6 3 9
This is the const version of topLeftCorner(Index, Index).
|
inlineinherited |
The template parameters CRows and CCols are the number of rows and columns in the corner.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topLeftCorner<2,2>(): 7 9 -2 -6 Now the matrix m is: 0 0 -5 -3 0 0 1 0 6 -3 0 9 6 6 3 9
|
inlineinherited |
This is the const version of topLeftCorner<int, int>().
| CRows | number of rows in corner as specified at compile-time |
| CCols | number of columns in corner as specified at compile-time |
| cRows | number of rows in corner as specified at run-time |
| cCols | number of columns in corner as specified at run-time |
This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topLeftCorner<2,Dynamic>(2,2): 7 9 -2 -6 Now the matrix m is: 0 0 -5 -3 0 0 1 0 6 -3 0 9 6 6 3 9
|
inlineinherited |
This is the const version of topLeftCorner<int, int>(Index, Index).
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topRightCorner(2, 2): -5 -3 1 0 Now the matrix m is: 7 9 0 0 -2 -6 0 0 6 -3 0 9 6 6 3 9
This is the const version of topRightCorner(Index, Index).
|
inlineinherited |
| CRows | the number of rows in the corner |
| CCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topRightCorner<2,2>(): -5 -3 1 0 Now the matrix m is: 7 9 0 0 -2 -6 0 0 6 -3 0 9 6 6 3 9
|
inlineinherited |
This is the const version of topRightCorner<int, int>().
| CRows | number of rows in corner as specified at compile-time |
| CCols | number of columns in corner as specified at compile-time |
| cRows | number of rows in corner as specified at run-time |
| cCols | number of columns in corner as specified at run-time |
This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topRightCorner<2,Dynamic>(2,2): -5 -3 1 0 Now the matrix m is: 7 9 0 0 -2 -6 0 0 6 -3 0 9 6 6 3 9
|
inlineinherited |
This is the const version of topRightCorner<int, int>(Index, Index).
|
inlineinherited |
| n | the number of rows in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.topRows(2): 7 9 -5 -3 -2 -6 1 0 Now the array a is: 0 0 0 0 0 0 0 0 6 -3 0 9 6 6 3 9
|
inlineinherited |
This is the const version of topRows(Index).
|
inlineinherited |
| N | the number of rows in the block as specified at compile-time |
| n | the number of rows in the block as specified at run-time |
The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.topRows<2>(): 7 9 -5 -3 -2 -6 1 0 Now the array a is: 0 0 0 0 0 0 0 0 6 -3 0 9 6 6 3 9
|
inlineinherited |
This is the const version of topRows<int>().
|
inline |
*this, i.e. the sum of the coefficients on the main diagonal.*this can be any matrix, not necessarily square.
|
inlineinherited |
Example:
Output:
Here is the matrix m: 7 6 -2 6 Here is the transpose of m: 7 -2 6 6 Here is the coefficient (1,0) in the transpose of m: 6 Let us overwrite this coefficient with the value 0. Now the matrix m is: 7 0 -2 6
Referenced by Hyperplane< _Scalar, _AmbientDim, Options >::Through().
|
inlineinherited |
This is the const version of transpose().
Make sure you read the warning for transpose() !
|
inlineinherited |
This is the "in place" version of transpose(): it replaces *this by its own transpose. Thus, doing
has the same effect on m as doing
and is faster and also safer because in the latter line of code, forgetting the eval() results in a bug caused by aliasing.
Notice however that this method is only useful if you want to replace a matrix by its own transpose. If you just need the transpose of a matrix, use transpose().
*this must be a resizable matrix. This excludes (non-square) fixed-size matrices, block-expressions and maps.References Eigen::Dynamic.
| MatrixBase<Derived>::template TriangularViewReturnType<Mode>::Type triangularView | ( | ) |
The parameter Mode can have the following values: Upper, StrictlyUpper, UnitUpper, Lower, StrictlyLower, UnitLower.
Example:
Output:
| MatrixBase<Derived>::template ConstTriangularViewReturnType<Mode>::Type triangularView | ( | ) | const |
This is the const version of MatrixBase::triangularView()
|
inline |
Apply a unary operator coefficient-wise.
| [in] | func | Functor implementing the unary operator |
| CustomUnaryOp | Type of func |
The function ptr_fun() from the C++ standard library can be used to make functors out of normal functions.
Example:
Output:
0.68 0.823 -0.444 -0.27
-0.211 -0.605 0.108 0.0268
0.566 -0.33 -0.0452 0.904
0.597 0.536 0.258 0.832
becomes:
0.68 0.823 0 0
0 0 0.108 0.0268
0.566 0 0 0.904
0.597 0.536 0.258 0.832
Genuine functors allow for more possibilities, for instance it may contain a state.
Example:
Output:
0.68 0.823 -0.444 -0.27
-0.211 -0.605 0.108 0.0268
0.566 -0.33 -0.0452 0.904
0.597 0.536 0.258 0.832
becomes:
0.5 0.5 -0.444 -0.27
-0.211 -0.5 0.108 0.0268
0.5 -0.33 -0.0452 0.5
0.5 0.5 0.258 0.5
|
inline |
The template parameter CustomUnaryOp is the type of the functor of the custom unary operator.
Example:
Output:
0.68 0.823 -0.444 -0.27
-0.211 -0.605 0.108 0.0268
0.566 -0.33 -0.0452 0.904
0.597 0.536 0.258 0.832
becomes:
0.5 0.5 -0.444 -0.27
-0.211 -0.5 0.108 0.0268
0.5 -0.33 -0.0452 0.5
0.5 0.5 0.258 0.5
|
inlinestatic |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inlinestatic |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is for fixed-size vector only.
| MatrixBase< Derived >::PlainObject unitOrthogonal | ( | void | ) | const |
*this The size of *this must be at least 2. If the size is exactly 2, then the returned vector is a counter clock wise rotation of *this, i.e., (-y,x).normalized().
|
inlinestatic |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inlinestatic |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inlinestatic |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inlinestatic |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
|
inlineinherited |
|
inherited |
Applies the visitor visitor to the whole coefficients of the matrix or vector.
The template parameter Visitor is the type of the visitor and provides the following interface:
References Eigen::Dynamic.
|
inlinestaticinherited |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.
Example:
Output:
0 0 0 0 0 0
The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.
Example:
Output:
0 0 0 0 0 0
|
inlinestaticinherited |
This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.
Example:
Output:
0 0 0 0 0 0 0 0
|
related |
Outputs the matrix, to the given stream.
If you wish to print the matrix with a format different than the default, use DenseBase::format().
It is also possible to change the default format by defining EIGEN_DEFAULT_IO_FORMAT before including Eigen headers. If not defined, this will automatically be defined to Eigen::IOFormat(), that is the Eigen::IOFormat with default parameters.
1.8.5