Detailed Description

template<typename _MatrixType, int _UpLo>
class Eigen::LDLT< _MatrixType, _UpLo >

Robust Cholesky decomposition of a matrix with pivoting.

Parameters

MatrixType	the type of the matrix of which to compute the LDL^T Cholesky decomposition
UpLo	the triangular part that will be used for the decompositon: Lower (default) or Upper. The other triangular part won't be read.

Perform a robust Cholesky decomposition of a positive semidefinite or negative semidefinite matrix $ A $ such that $ A = P^TLDL^*P $ , where P is a permutation matrix, L is lower triangular with a unit diagonal and D is a diagonal matrix.

The decomposition uses pivoting to ensure stability, so that L will have zeros in the bottom right rank(A) - n submatrix. Avoiding the square root on D also stabilizes the computation.

Remember that Cholesky decompositions are not rank-revealing. Also, do not use a Cholesky decomposition to determine whether a system of equations has a solution.

See Also: MatrixBase::ldlt(), class LLT

Public Member Functions
LDLT &	compute (const MatrixType &matrix)

ComputationInfo	info () const
	Reports whether previous computation was successful. More...

bool	isNegative (void) const

bool	isPositive () const

	LDLT ()
	Default Constructor. More...

	LDLT (Index size)
	Default Constructor with memory preallocation. More...

	LDLT (const MatrixType &matrix)
	Constructor with decomposition. More...

Traits::MatrixL	matrixL () const

const MatrixType &	matrixLDLT () const

Traits::MatrixU	matrixU () const

template<typename Derived >
LDLT< MatrixType, _UpLo > &	rankUpdate (const MatrixBase< Derived > &w, const typename LDLT< MatrixType, _UpLo >::RealScalar &sigma)

MatrixType	reconstructedMatrix () const

void	setZero ()

template<typename Rhs >
const internal::solve_retval < LDLT, Rhs >	solve (const MatrixBase< Rhs > &b) const

const TranspositionType &	transpositionsP () const

Diagonal< const MatrixType >	vectorD () const

Constructor & Destructor Documentation

LDLT ( )

inline

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via LDLT::compute(const MatrixType&).

LDLT ( Index size )

inline

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See Also: LDLT()

LDLT ( const MatrixType & matrix )

inline

Constructor with decomposition.

This calculates the decomposition for the input matrix.

See Also: LDLT(Index size)

References LDLT< _MatrixType, _UpLo >::compute().

Member Function Documentation

LDLT< MatrixType, _UpLo > & compute ( const MatrixType & a )

Compute / recompute the LDLT decomposition A = L D L^* = U^* D U of matrix

Referenced by LDLT< _MatrixType, _UpLo >::LDLT().

ComputationInfo info ( ) const

inline

Reports whether previous computation was successful.

Returns: Success if computation was succesful, NumericalIssue if the matrix.appears to be negative.

References Eigen::Success.

bool isNegative ( void ) const

inline

Returns: true if the matrix is negative (semidefinite)

bool isPositive ( ) const

inline

Returns: true if the matrix is positive (semidefinite)

Traits::MatrixL matrixL ( ) const

inline

Returns: a view of the lower triangular matrix L

const MatrixType& matrixLDLT ( ) const

inline

Returns: the internal LDLT decomposition matrix

TODO: document the storage layout

Traits::MatrixU matrixU ( ) const

inline

Returns: a view of the upper triangular matrix U

LDLT<MatrixType,_UpLo>& rankUpdate	(	const MatrixBase< Derived > &	w,
		const typename LDLT< MatrixType, _UpLo >::RealScalar &	sigma
	)

Update the LDLT decomposition: given A = L D L^T, efficiently compute the decomposition of A + sigma w w^T.

Parameters

w	a vector to be incorporated into the decomposition.
sigma	a scalar, +1 for updates and -1 for "downdates," which correspond to removing previously-added column vectors. Optional; default value is +1.

See Also: setZero()

MatrixType reconstructedMatrix ( ) const

Returns: the matrix represented by the decomposition, i.e., it returns the product: P^T L D L^* P. This function is provided for debug purpose.

void setZero ( )

inline

Clear any existing decomposition

See Also: rankUpdate(w,sigma)

const internal::solve_retval<LDLT, Rhs> solve ( const MatrixBase< Rhs > & b ) const

inline

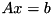Returns: a solution x of using the current decomposition of A.

This function also supports in-place solves using the syntax x = decompositionObject.solve(x) .

This method just tries to find as good a solution as possible. If you want to check whether a solution exists or if it is accurate, just call this function to get a result and then compute the error of this result, or use MatrixBase::isApprox() directly, for instance like this:

bool a_solution_exists = (A*result).isApprox(b, precision);

This method avoids dividing by zero, so that the non-existence of a solution doesn't by itself mean that you'll get inf or nan values.

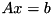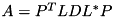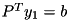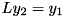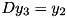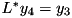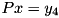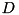More precisely, this method solves $ A x = b $ using the decomposition $ A = P^T L D L^* P $ by solving the systems $ P^T y_1 = b $ , $ L y_2 = y_1 $ , $ D y_3 = y_2 $ , $ L^* y_4 = y_3 $ and $ P x = y_4 $ in succession. If the matrix $ A $ is singular, then $ D $ will also be singular (all the other matrices are invertible). In that case, the least-square solution of 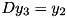is computed. This does not mean that this function computes the least-square solution of 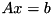$ A x = b $ is $ A $ is singular.