template<typename Derived>
class Eigen::SimplicialCholeskyBase< Derived >
A direct sparse Cholesky factorizations.
These classes provide LL^T and LDL^T Cholesky factorizations of sparse matrices that are selfadjoint and positive definite. The factorization allows for solving A.X = B where X and B can be either dense or sparse.
In order to reduce the fill-in, a symmetric permutation P is applied prior to the factorization such that the factorized matrix is P A P^-1.
- Template Parameters
-
| _MatrixType | the type of the sparse matrix A, it must be a SparseMatrix<> |
| _UpLo | the triangular part that will be used for the computations. It can be Lower or Upper. Default is Lower. |
Inherits noncopyable.
| Derived& setShift |
( |
const RealScalar & |
offset, |
|
|
const RealScalar & |
scale = 1 |
|
) |
| |
|
inline |
Sets the shift parameters that will be used to adjust the diagonal coefficients during the numerical factorization.
During the numerical factorization, the diagonal coefficients are transformed by the following linear model:
d_ii = offset + scale * d_ii
The default is the identity transformation with offset=0, and scale=1.
- Returns
- a reference to
*this.


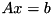 using the current decomposition of A.
using the current decomposition of A.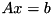 using the current decomposition of A.
using the current decomposition of A.