 |
Eigen
3.2.7
|
 |
Eigen
3.2.7
|
A sparse direct LU factorization and solver based on the SuperLU library.
This class allows to solve for A.X = B sparse linear problems via a direct LU factorization using the SuperLU library. The sparse matrix A must be squared and invertible. The vectors or matrices X and B can be either dense or sparse.
| _MatrixType | the type of the sparse matrix A, it must be a SparseMatrix<> |
 Inheritance diagram for SuperLU< _MatrixType >:
Inheritance diagram for SuperLU< _MatrixType >:Public Member Functions | |
| void | analyzePattern (const MatrixType &matrix) |
| void | compute (const MatrixType &matrix) |
| void | factorize (const MatrixType &matrix) |
| ComputationInfo | info () const |
| Reports whether previous computation was successful. More... | |
| superlu_options_t & | options () |
| const internal::solve_retval < SuperLUBase, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| const internal::sparse_solve_retval < SuperLUBase, Rhs > | solve (const SparseMatrixBase< Rhs > &b) const |
|
inline |
Performs a symbolic decomposition on the sparcity of matrix.
This function is particularly useful when solving for several problems having the same structure.
References SuperLUBase< _MatrixType, Derived >::analyzePattern(), and Eigen::InvalidInput.
|
inlineinherited |
Computes the sparse Cholesky decomposition of matrix
| void factorize | ( | const MatrixType & | matrix | ) |
Performs a numeric decomposition of matrix
The given matrix must has the same sparcity than the matrix on which the symbolic decomposition has been performed.
References Eigen::InvalidInput, Eigen::NumericalIssue, and Eigen::Success.
|
inlineinherited |
Reports whether previous computation was successful.
Success if computation was succesful, NumericalIssue if the matrix.appears to be negative.
|
inlineinherited |
|
inlineinherited |
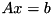 using the current decomposition of A.
using the current decomposition of A.
|
inlineinherited |
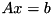 using the current decomposition of A.
using the current decomposition of A.