 |
OpenCV
3.0.0-dev
Open Source Computer Vision
|
 |
OpenCV
3.0.0-dev
Open Source Computer Vision
|
Classes | |
| class | cv::LDA |
| Linear Discriminant Analysis. More... | |
| class | cv::PCA |
| Principal Component Analysis. More... | |
| class | cv::RNG |
| Random Number Generator. More... | |
| class | cv::RNG_MT19937 |
| Mersenne Twister random number generator. More... | |
| class | cv::SVD |
| Singular Value Decomposition. More... | |
Functions | |
| void | cv::absdiff (InputArray src1, InputArray src2, OutputArray dst) |
| Calculates the per-element absolute difference between two arrays or between an array and a scalar. More... | |
| void | cv::add (InputArray src1, InputArray src2, OutputArray dst, InputArray mask=noArray(), int dtype=-1) |
| Calculates the per-element sum of two arrays or an array and a scalar. More... | |
| void | cv::addWeighted (InputArray src1, double alpha, InputArray src2, double beta, double gamma, OutputArray dst, int dtype=-1) |
| Calculates the weighted sum of two arrays. More... | |
| void | cv::batchDistance (InputArray src1, InputArray src2, OutputArray dist, int dtype, OutputArray nidx, int normType=NORM_L2, int K=0, InputArray mask=noArray(), int update=0, bool crosscheck=false) |
| naive nearest neighbor finder More... | |
| void | cv::bitwise_and (InputArray src1, InputArray src2, OutputArray dst, InputArray mask=noArray()) |
| computes bitwise conjunction of the two arrays (dst = src1 & src2) Calculates the per-element bit-wise conjunction of two arrays or an array and a scalar. More... | |
| void | cv::bitwise_not (InputArray src, OutputArray dst, InputArray mask=noArray()) |
| Inverts every bit of an array. More... | |
| void | cv::bitwise_or (InputArray src1, InputArray src2, OutputArray dst, InputArray mask=noArray()) |
| Calculates the per-element bit-wise disjunction of two arrays or an array and a scalar. More... | |
| void | cv::bitwise_xor (InputArray src1, InputArray src2, OutputArray dst, InputArray mask=noArray()) |
| Calculates the per-element bit-wise "exclusive or" operation on two arrays or an array and a scalar. More... | |
| int | cv::borderInterpolate (int p, int len, int borderType) |
| Computes the source location of an extrapolated pixel. More... | |
| void | cv::calcCovarMatrix (const Mat *samples, int nsamples, Mat &covar, Mat &mean, int flags, int ctype=CV_64F) |
| Calculates the covariance matrix of a set of vectors. More... | |
| void | cv::calcCovarMatrix (InputArray samples, OutputArray covar, InputOutputArray mean, int flags, int ctype=CV_64F) |
| void | cv::cartToPolar (InputArray x, InputArray y, OutputArray magnitude, OutputArray angle, bool angleInDegrees=false) |
| Calculates the magnitude and angle of 2D vectors. More... | |
| bool | cv::checkRange (InputArray a, bool quiet=true, Point *pos=0, double minVal=-DBL_MAX, double maxVal=DBL_MAX) |
| Checks every element of an input array for invalid values. More... | |
| void | cv::compare (InputArray src1, InputArray src2, OutputArray dst, int cmpop) |
| Performs the per-element comparison of two arrays or an array and scalar value. More... | |
| void | cv::completeSymm (InputOutputArray mtx, bool lowerToUpper=false) |
| Copies the lower or the upper half of a square matrix to another half. More... | |
| void | cv::convertScaleAbs (InputArray src, OutputArray dst, double alpha=1, double beta=0) |
| Scales, calculates absolute values, and converts the result to 8-bit. More... | |
| void | cv::copyMakeBorder (InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar &value=Scalar()) |
| Forms a border around an image. More... | |
| int | cv::countNonZero (InputArray src) |
| Counts non-zero array elements. More... | |
| void | cv::dct (InputArray src, OutputArray dst, int flags=0) |
| Performs a forward or inverse discrete Cosine transform of 1D or 2D array. More... | |
| double | cv::determinant (InputArray mtx) |
| Returns the determinant of a square floating-point matrix. More... | |
| void | cv::dft (InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0) |
| Performs a forward or inverse Discrete Fourier transform of a 1D or 2D floating-point array. More... | |
| void | cv::divide (InputArray src1, InputArray src2, OutputArray dst, double scale=1, int dtype=-1) |
| Performs per-element division of two arrays or a scalar by an array. More... | |
| void | cv::divide (double scale, InputArray src2, OutputArray dst, int dtype=-1) |
| bool | cv::eigen (InputArray src, OutputArray eigenvalues, OutputArray eigenvectors=noArray()) |
| Calculates eigenvalues and eigenvectors of a symmetric matrix. More... | |
| void | cv::exp (InputArray src, OutputArray dst) |
| Calculates the exponent of every array element. More... | |
| void | cv::extractChannel (InputArray src, OutputArray dst, int coi) |
| extracts a single channel from src (coi is 0-based index) More... | |
| void | cv::findNonZero (InputArray src, OutputArray idx) |
| Returns the list of locations of non-zero pixels. More... | |
| void | cv::flip (InputArray src, OutputArray dst, int flipCode) |
| Flips a 2D array around vertical, horizontal, or both axes. More... | |
| void | cv::gemm (InputArray src1, InputArray src2, double alpha, InputArray src3, double beta, OutputArray dst, int flags=0) |
| Performs generalized matrix multiplication. More... | |
| int | cv::getOptimalDFTSize (int vecsize) |
| Returns the optimal DFT size for a given vector size. More... | |
| void | cv::hconcat (const Mat *src, size_t nsrc, OutputArray dst) |
| Applies horizontal concatenation to given matrices. More... | |
| void | cv::hconcat (InputArray src1, InputArray src2, OutputArray dst) |
| void | cv::hconcat (InputArrayOfArrays src, OutputArray dst) |
| void | cv::idct (InputArray src, OutputArray dst, int flags=0) |
| Calculates the inverse Discrete Cosine Transform of a 1D or 2D array. More... | |
| void | cv::idft (InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0) |
| Calculates the inverse Discrete Fourier Transform of a 1D or 2D array. More... | |
| void | cv::inRange (InputArray src, InputArray lowerb, InputArray upperb, OutputArray dst) |
| Checks if array elements lie between the elements of two other arrays. More... | |
| void | cv::insertChannel (InputArray src, InputOutputArray dst, int coi) |
| inserts a single channel to dst (coi is 0-based index) More... | |
| double | cv::invert (InputArray src, OutputArray dst, int flags=DECOMP_LU) |
| Finds the inverse or pseudo-inverse of a matrix. More... | |
| void | cv::log (InputArray src, OutputArray dst) |
| Calculates the natural logarithm of every array element. More... | |
| void | cv::LUT (InputArray src, InputArray lut, OutputArray dst) |
| Performs a look-up table transform of an array. More... | |
| void | cv::magnitude (InputArray x, InputArray y, OutputArray magnitude) |
| Calculates the magnitude of 2D vectors. More... | |
| double | cv::Mahalanobis (InputArray v1, InputArray v2, InputArray icovar) |
| Calculates the Mahalanobis distance between two vectors. More... | |
| void | cv::max (InputArray src1, InputArray src2, OutputArray dst) |
| Calculates per-element maximum of two arrays or an array and a scalar. More... | |
| void | cv::max (const Mat &src1, const Mat &src2, Mat &dst) |
| void | cv::max (const UMat &src1, const UMat &src2, UMat &dst) |
| Scalar | cv::mean (InputArray src, InputArray mask=noArray()) |
| Calculates an average (mean) of array elements. More... | |
| void | cv::meanStdDev (InputArray src, OutputArray mean, OutputArray stddev, InputArray mask=noArray()) |
| void | cv::merge (const Mat *mv, size_t count, OutputArray dst) |
| Creates one multichannel array out of several single-channel ones. More... | |
| void | cv::merge (InputArrayOfArrays mv, OutputArray dst) |
| void | cv::min (InputArray src1, InputArray src2, OutputArray dst) |
| Calculates per-element minimum of two arrays or an array and a scalar. More... | |
| void | cv::min (const Mat &src1, const Mat &src2, Mat &dst) |
| void | cv::min (const UMat &src1, const UMat &src2, UMat &dst) |
| void | cv::minMaxIdx (InputArray src, double *minVal, double *maxVal=0, int *minIdx=0, int *maxIdx=0, InputArray mask=noArray()) |
| Finds the global minimum and maximum in an array. More... | |
| void | cv::minMaxLoc (InputArray src, double *minVal, double *maxVal=0, Point *minLoc=0, Point *maxLoc=0, InputArray mask=noArray()) |
| Finds the global minimum and maximum in an array. More... | |
| void | cv::minMaxLoc (const SparseMat &a, double *minVal, double *maxVal, int *minIdx=0, int *maxIdx=0) |
| void | cv::mixChannels (const Mat *src, size_t nsrcs, Mat *dst, size_t ndsts, const int *fromTo, size_t npairs) |
| Copies specified channels from input arrays to the specified channels of output arrays. More... | |
| void | cv::mixChannels (InputArrayOfArrays src, InputOutputArrayOfArrays dst, const int *fromTo, size_t npairs) |
| void | cv::mixChannels (InputArrayOfArrays src, InputOutputArrayOfArrays dst, const std::vector< int > &fromTo) |
| void | cv::mulSpectrums (InputArray a, InputArray b, OutputArray c, int flags, bool conjB=false) |
| Performs the per-element multiplication of two Fourier spectrums. More... | |
| void | cv::multiply (InputArray src1, InputArray src2, OutputArray dst, double scale=1, int dtype=-1) |
| Calculates the per-element scaled product of two arrays. More... | |
| void | cv::mulTransposed (InputArray src, OutputArray dst, bool aTa, InputArray delta=noArray(), double scale=1, int dtype=-1) |
| Calculates the product of a matrix and its transposition. More... | |
| double | cv::norm (InputArray src1, int normType=NORM_L2, InputArray mask=noArray()) |
| Calculates an absolute array norm, an absolute difference norm, or a relative difference norm. More... | |
| double | cv::norm (InputArray src1, InputArray src2, int normType=NORM_L2, InputArray mask=noArray()) |
| double | cv::norm (const SparseMat &src, int normType) |
| void | cv::normalize (InputArray src, InputOutputArray dst, double alpha=1, double beta=0, int norm_type=NORM_L2, int dtype=-1, InputArray mask=noArray()) |
| Normalizes the norm or value range of an array. More... | |
| void | cv::normalize (const SparseMat &src, SparseMat &dst, double alpha, int normType) |
| void | cv::patchNaNs (InputOutputArray a, double val=0) |
| converts NaN's to the given number More... | |
| void | cv::PCABackProject (InputArray data, InputArray mean, InputArray eigenvectors, OutputArray result) |
| void | cv::PCACompute (InputArray data, InputOutputArray mean, OutputArray eigenvectors, int maxComponents=0) |
| void | cv::PCACompute (InputArray data, InputOutputArray mean, OutputArray eigenvectors, double retainedVariance) |
| void | cv::PCAProject (InputArray data, InputArray mean, InputArray eigenvectors, OutputArray result) |
| void | cv::perspectiveTransform (InputArray src, OutputArray dst, InputArray m) |
| Performs the perspective matrix transformation of vectors. More... | |
| void | cv::phase (InputArray x, InputArray y, OutputArray angle, bool angleInDegrees=false) |
| Calculates the rotation angle of 2D vectors. More... | |
| void | cv::polarToCart (InputArray magnitude, InputArray angle, OutputArray x, OutputArray y, bool angleInDegrees=false) |
| Calculates x and y coordinates of 2D vectors from their magnitude and angle. More... | |
| void | cv::pow (InputArray src, double power, OutputArray dst) |
| Raises every array element to a power. More... | |
| double | cv::PSNR (InputArray src1, InputArray src2) |
| computes PSNR image/video quality metric More... | |
| void | cv::randn (InputOutputArray dst, InputArray mean, InputArray stddev) |
| Fills the array with normally distributed random numbers. More... | |
| void | cv::randShuffle (InputOutputArray dst, double iterFactor=1., RNG *rng=0) |
| Shuffles the array elements randomly. More... | |
| void | cv::randu (InputOutputArray dst, InputArray low, InputArray high) |
| Generates a single uniformly-distributed random number or an array of random numbers. More... | |
| void | cv::reduce (InputArray src, OutputArray dst, int dim, int rtype, int dtype=-1) |
| Reduces a matrix to a vector. More... | |
| void | cv::repeat (InputArray src, int ny, int nx, OutputArray dst) |
| Fills the output array with repeated copies of the input array. More... | |
| Mat | cv::repeat (const Mat &src, int ny, int nx) |
| void | cv::scaleAdd (InputArray src1, double alpha, InputArray src2, OutputArray dst) |
| Calculates the sum of a scaled array and another array. More... | |
| void | cv::setIdentity (InputOutputArray mtx, const Scalar &s=Scalar(1)) |
| Initializes a scaled identity matrix. More... | |
| bool | cv::solve (InputArray src1, InputArray src2, OutputArray dst, int flags=DECOMP_LU) |
| Solves one or more linear systems or least-squares problems. More... | |
| int | cv::solveCubic (InputArray coeffs, OutputArray roots) |
| Finds the real roots of a cubic equation. More... | |
| double | cv::solvePoly (InputArray coeffs, OutputArray roots, int maxIters=300) |
| Finds the real or complex roots of a polynomial equation. More... | |
| void | cv::sort (InputArray src, OutputArray dst, int flags) |
| Sorts each row or each column of a matrix. More... | |
| void | cv::sortIdx (InputArray src, OutputArray dst, int flags) |
| Sorts each row or each column of a matrix. More... | |
| void | cv::split (const Mat &src, Mat *mvbegin) |
| Divides a multi-channel array into several single-channel arrays. More... | |
| void | cv::split (InputArray m, OutputArrayOfArrays mv) |
| void | cv::sqrt (InputArray src, OutputArray dst) |
| Calculates a square root of array elements. More... | |
| void | cv::subtract (InputArray src1, InputArray src2, OutputArray dst, InputArray mask=noArray(), int dtype=-1) |
| Calculates the per-element difference between two arrays or array and a scalar. More... | |
| Scalar | cv::sum (InputArray src) |
| Calculates the sum of array elements. More... | |
| void | cv::SVBackSubst (InputArray w, InputArray u, InputArray vt, InputArray rhs, OutputArray dst) |
| void | cv::SVDecomp (InputArray src, OutputArray w, OutputArray u, OutputArray vt, int flags=0) |
| RNG & | cv::theRNG () |
| Returns the default random number generator. More... | |
| Scalar | cv::trace (InputArray mtx) |
| Returns the trace of a matrix. More... | |
| void | cv::transform (InputArray src, OutputArray dst, InputArray m) |
| Performs the matrix transformation of every array element. More... | |
| void | cv::transpose (InputArray src, OutputArray dst) |
| Transposes a matrix. More... | |
| void | cv::vconcat (const Mat *src, size_t nsrc, OutputArray dst) |
| Applies vertical concatenation to given matrices. More... | |
| void | cv::vconcat (InputArray src1, InputArray src2, OutputArray dst) |
| void | cv::vconcat (InputArrayOfArrays src, OutputArray dst) |
| enum cv::BorderTypes |
Various border types, image boundaries are denoted with |
| enum cv::CmpTypes |
| enum cv::DecompTypes |
matrix decomposition types
| Enumerator | |
|---|---|
| DECOMP_LU |
Gaussian elimination with the optimal pivot element chosen. |
| DECOMP_SVD |
singular value decomposition (SVD) method; the system can be over-defined and/or the matrix src1 can be singular |
| DECOMP_EIG |
eigenvalue decomposition; the matrix src1 must be symmetrical |
| DECOMP_CHOLESKY |
Cholesky \(LL^T\) factorization; the matrix src1 must be symmetrical and positively defined |
| DECOMP_QR |
QR factorization; the system can be over-defined and/or the matrix src1 can be singular |
| DECOMP_NORMAL |
while all the previous flags are mutually exclusive, this flag can be used together with any of the previous; it means that the normal equations \(\texttt{src1}^T\cdot\texttt{src1}\cdot\texttt{dst}=\texttt{src1}^T\texttt{src2}\) are solved instead of the original system \(\texttt{src1}\cdot\texttt{dst}=\texttt{src2}\) |
| enum cv::DftFlags |
| enum cv::PCA::Flags |
| enum cv::SVD::Flags |
| enum cv::GemmFlags |
| enum cv::NormTypes |
norm types
\[norm = \forkthree{\|\texttt{src1}\|_{L_{\infty}} = \max _I | \texttt{src1} (I)|}{if \(\texttt{normType} = \texttt{NORM_INF}\) } { \| \texttt{src1} \| _{L_1} = \sum _I | \texttt{src1} (I)|}{if \(\texttt{normType} = \texttt{NORM_L1}\) } { \| \texttt{src1} \| _{L_2} = \sqrt{\sum_I \texttt{src1}(I)^2} }{if \(\texttt{normType} = \texttt{NORM_L2}\) }\]
\[norm = \forkthree{\|\texttt{src1}-\texttt{src2}\|_{L_{\infty}} = \max _I | \texttt{src1} (I) - \texttt{src2} (I)|}{if \(\texttt{normType} = \texttt{NORM_INF}\) } { \| \texttt{src1} - \texttt{src2} \| _{L_1} = \sum _I | \texttt{src1} (I) - \texttt{src2} (I)|}{if \(\texttt{normType} = \texttt{NORM_L1}\) } { \| \texttt{src1} - \texttt{src2} \| _{L_2} = \sqrt{\sum_I (\texttt{src1}(I) - \texttt{src2}(I))^2} }{if \(\texttt{normType} = \texttt{NORM_L2}\) }\]
\[norm = \forkthree{\frac{\|\texttt{src1}-\texttt{src2}\|_{L_{\infty}} }{\|\texttt{src2}\|_{L_{\infty}} }}{if \(\texttt{normType} = \texttt{NORM_RELATIVE_INF}\) } { \frac{\|\texttt{src1}-\texttt{src2}\|_{L_1} }{\|\texttt{src2}\|_{L_1}} }{if \(\texttt{normType} = \texttt{NORM_RELATIVE_L1}\) } { \frac{\|\texttt{src1}-\texttt{src2}\|_{L_2} }{\|\texttt{src2}\|_{L_2}} }{if \(\texttt{normType} = \texttt{NORM_RELATIVE_L2}\) }\]
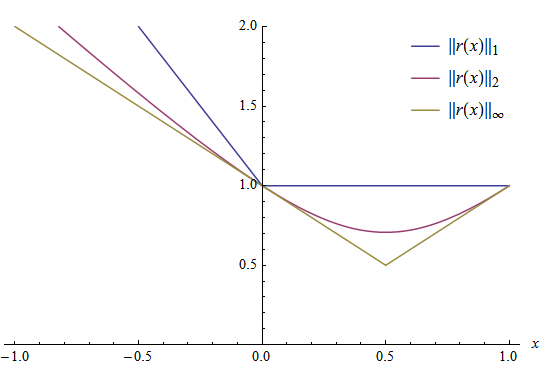
As example for one array consider the function \(r(x)= \begin{pmatrix} x \\ 1-x \end{pmatrix}, x \in [-1;1]\). The \( L_{1}, L_{2} \) and \( L_{\infty} \) norm for the sample value \(r(-1) = \begin{pmatrix} -1 \\ 2 \end{pmatrix}\) is calculated as follows
\begin{align*} \| r(-1) \|_{L_1} &= |-1| + |2| = 3 \\ \| r(-1) \|_{L_2} &= \sqrt{(-1)^{2} + (2)^{2}} = \sqrt{5} \\ \| r(-1) \|_{L_\infty} &= \max(|-1|,|2|) = 2 \end{align*}
and for \(r(0.5) = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix}\) the calculation is
\begin{align*} \| r(0.5) \|_{L_1} &= |0.5| + |0.5| = 1 \\ \| r(0.5) \|_{L_2} &= \sqrt{(0.5)^{2} + (0.5)^{2}} = \sqrt{0.5} \\ \| r(0.5) \|_{L_\infty} &= \max(|0.5|,|0.5|) = 0.5. \end{align*}
The following graphic shows all values for the three norm functions \(\| r(x) \|_{L_1}, \| r(x) \|_{L_2}\) and \(\| r(x) \|_{L_\infty}\). It is notable that the \( L_{1} \) norm forms the upper and the \( L_{\infty} \) norm forms the lower border for the example function \( r(x) \).
| Enumerator | |
|---|---|
| NORM_INF | |
| NORM_L1 | |
| NORM_L2 | |
| NORM_L2SQR | |
| NORM_HAMMING | |
| NORM_HAMMING2 | |
| NORM_TYPE_MASK | |
| NORM_RELATIVE |
flag |
| NORM_MINMAX |
flag |
| void cv::absdiff | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst | ||
| ) |
Calculates the per-element absolute difference between two arrays or between an array and a scalar.
The function absdiff calculates: Absolute difference between two arrays when they have the same size and type:
\[\texttt{dst}(I) = \texttt{saturate} (| \texttt{src1}(I) - \texttt{src2}(I)|)\]
Absolute difference between an array and a scalar when the second array is constructed from Scalar or has as many elements as the number of channels in src1:
\[\texttt{dst}(I) = \texttt{saturate} (| \texttt{src1}(I) - \texttt{src2} |)\]
Absolute difference between a scalar and an array when the first array is constructed from Scalar or has as many elements as the number of channels in src2:
\[\texttt{dst}(I) = \texttt{saturate} (| \texttt{src1} - \texttt{src2}(I) |)\]
where I is a multi-dimensional index of array elements. In case of multi-channel arrays, each channel is processed independently.
| src1 | first input array or a scalar. |
| src2 | second input array or a scalar. |
| dst | output array that has the same size and type as input arrays. |
| void cv::add | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| InputArray | mask = noArray(), |
||
| int | dtype = -1 |
||
| ) |
Calculates the per-element sum of two arrays or an array and a scalar.
The function add calculates:
\[\texttt{dst}(I) = \texttt{saturate} ( \texttt{src1}(I) + \texttt{src2}(I)) \quad \texttt{if mask}(I) \ne0\]
src1.channels(): \[\texttt{dst}(I) = \texttt{saturate} ( \texttt{src1}(I) + \texttt{src2} ) \quad \texttt{if mask}(I) \ne0\]
src2.channels(): \[\texttt{dst}(I) = \texttt{saturate} ( \texttt{src1} + \texttt{src2}(I) ) \quad \texttt{if mask}(I) \ne0\]
whereI is a multi-dimensional index of array elements. In case of multi-channel arrays, each channel is processed independently.The first function in the list above can be replaced with matrix expressions:
The input arrays and the output array can all have the same or different depths. For example, you can add a 16-bit unsigned array to a 8-bit signed array and store the sum as a 32-bit floating-point array. Depth of the output array is determined by the dtype parameter. In the second and third cases above, as well as in the first case, when src1.depth() == src2.depth(), dtype can be set to the default -1. In this case, the output array will have the same depth as the input array, be it src1, src2 or both.
| src1 | first input array or a scalar. |
| src2 | second input array or a scalar. |
| dst | output array that has the same size and number of channels as the input array(s); the depth is defined by dtype or src1/src2. |
| mask | optional operation mask - 8-bit single channel array, that specifies elements of the output array to be changed. |
| dtype | optional depth of the output array (see the discussion below). |
| void cv::addWeighted | ( | InputArray | src1, |
| double | alpha, | ||
| InputArray | src2, | ||
| double | beta, | ||
| double | gamma, | ||
| OutputArray | dst, | ||
| int | dtype = -1 |
||
| ) |
Calculates the weighted sum of two arrays.
The function addWeighted calculates the weighted sum of two arrays as follows:
\[\texttt{dst} (I)= \texttt{saturate} ( \texttt{src1} (I)* \texttt{alpha} + \texttt{src2} (I)* \texttt{beta} + \texttt{gamma} )\]
where I is a multi-dimensional index of array elements. In case of multi-channel arrays, each channel is processed independently. The function can be replaced with a matrix expression:
| src1 | first input array. |
| alpha | weight of the first array elements. |
| src2 | second input array of the same size and channel number as src1. |
| beta | weight of the second array elements. |
| gamma | scalar added to each sum. |
| dst | output array that has the same size and number of channels as the input arrays. |
| dtype | optional depth of the output array; when both input arrays have the same depth, dtype can be set to -1, which will be equivalent to src1.depth(). |
| void cv::batchDistance | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dist, | ||
| int | dtype, | ||
| OutputArray | nidx, | ||
| int | normType = NORM_L2, |
||
| int | K = 0, |
||
| InputArray | mask = noArray(), |
||
| int | update = 0, |
||
| bool | crosscheck = false |
||
| ) |
naive nearest neighbor finder
see http://en.wikipedia.org/wiki/Nearest_neighbor_search
| void cv::bitwise_and | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| InputArray | mask = noArray() |
||
| ) |
computes bitwise conjunction of the two arrays (dst = src1 & src2) Calculates the per-element bit-wise conjunction of two arrays or an array and a scalar.
The function calculates the per-element bit-wise logical conjunction for: Two arrays when src1 and src2 have the same size:
\[\texttt{dst} (I) = \texttt{src1} (I) \wedge \texttt{src2} (I) \quad \texttt{if mask} (I) \ne0\]
An array and a scalar when src2 is constructed from Scalar or has the same number of elements as src1.channels():
\[\texttt{dst} (I) = \texttt{src1} (I) \wedge \texttt{src2} \quad \texttt{if mask} (I) \ne0\]
A scalar and an array when src1 is constructed from Scalar or has the same number of elements as src2.channels():
\[\texttt{dst} (I) = \texttt{src1} \wedge \texttt{src2} (I) \quad \texttt{if mask} (I) \ne0\]
In case of floating-point arrays, their machine-specific bit representations (usually IEEE754-compliant) are used for the operation. In case of multi-channel arrays, each channel is processed independently. In the second and third cases above, the scalar is first converted to the array type.
| src1 | first input array or a scalar. |
| src2 | second input array or a scalar. |
| dst | output array that has the same size and type as the input arrays. |
| mask | optional operation mask, 8-bit single channel array, that specifies elements of the output array to be changed. |
| void cv::bitwise_not | ( | InputArray | src, |
| OutputArray | dst, | ||
| InputArray | mask = noArray() |
||
| ) |
Inverts every bit of an array.
The function calculates per-element bit-wise inversion of the input array:
\[\texttt{dst} (I) = \neg \texttt{src} (I)\]
In case of a floating-point input array, its machine-specific bit representation (usually IEEE754-compliant) is used for the operation. In case of multi-channel arrays, each channel is processed independently.
| src | input array. |
| dst | output array that has the same size and type as the input array. |
| mask | optional operation mask, 8-bit single channel array, that specifies elements of the output array to be changed. |
| void cv::bitwise_or | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| InputArray | mask = noArray() |
||
| ) |
Calculates the per-element bit-wise disjunction of two arrays or an array and a scalar.
The function calculates the per-element bit-wise logical disjunction for: Two arrays when src1 and src2 have the same size:
\[\texttt{dst} (I) = \texttt{src1} (I) \vee \texttt{src2} (I) \quad \texttt{if mask} (I) \ne0\]
An array and a scalar when src2 is constructed from Scalar or has the same number of elements as src1.channels():
\[\texttt{dst} (I) = \texttt{src1} (I) \vee \texttt{src2} \quad \texttt{if mask} (I) \ne0\]
A scalar and an array when src1 is constructed from Scalar or has the same number of elements as src2.channels():
\[\texttt{dst} (I) = \texttt{src1} \vee \texttt{src2} (I) \quad \texttt{if mask} (I) \ne0\]
In case of floating-point arrays, their machine-specific bit representations (usually IEEE754-compliant) are used for the operation. In case of multi-channel arrays, each channel is processed independently. In the second and third cases above, the scalar is first converted to the array type.
| src1 | first input array or a scalar. |
| src2 | second input array or a scalar. |
| dst | output array that has the same size and type as the input arrays. |
| mask | optional operation mask, 8-bit single channel array, that specifies elements of the output array to be changed. |
| void cv::bitwise_xor | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| InputArray | mask = noArray() |
||
| ) |
Calculates the per-element bit-wise "exclusive or" operation on two arrays or an array and a scalar.
The function calculates the per-element bit-wise logical "exclusive-or" operation for: Two arrays when src1 and src2 have the same size:
\[\texttt{dst} (I) = \texttt{src1} (I) \oplus \texttt{src2} (I) \quad \texttt{if mask} (I) \ne0\]
An array and a scalar when src2 is constructed from Scalar or has the same number of elements as src1.channels():
\[\texttt{dst} (I) = \texttt{src1} (I) \oplus \texttt{src2} \quad \texttt{if mask} (I) \ne0\]
A scalar and an array when src1 is constructed from Scalar or has the same number of elements as src2.channels():
\[\texttt{dst} (I) = \texttt{src1} \oplus \texttt{src2} (I) \quad \texttt{if mask} (I) \ne0\]
In case of floating-point arrays, their machine-specific bit representations (usually IEEE754-compliant) are used for the operation. In case of multi-channel arrays, each channel is processed independently. In the 2nd and 3rd cases above, the scalar is first converted to the array type.
| src1 | first input array or a scalar. |
| src2 | second input array or a scalar. |
| dst | output array that has the same size and type as the input arrays. |
| mask | optional operation mask, 8-bit single channel array, that specifies elements of the output array to be changed. |
| int cv::borderInterpolate | ( | int | p, |
| int | len, | ||
| int | borderType | ||
| ) |
Computes the source location of an extrapolated pixel.
The function computes and returns the coordinate of a donor pixel corresponding to the specified extrapolated pixel when using the specified extrapolation border mode. For example, if you use cv::BORDER_WRAP mode in the horizontal direction, cv::BORDER_REFLECT_101 in the vertical direction and want to compute value of the "virtual" pixel Point(-5, 100) in a floating-point image img , it looks like:
Normally, the function is not called directly. It is used inside filtering functions and also in copyMakeBorder.
| p | 0-based coordinate of the extrapolated pixel along one of the axes, likely <0 or >= len |
| len | Length of the array along the corresponding axis. |
| borderType | Border type, one of the cv::BorderTypes, except for cv::BORDER_TRANSPARENT and cv::BORDER_ISOLATED . When borderType==cv::BORDER_CONSTANT , the function always returns -1, regardless of p and len. |
| void cv::calcCovarMatrix | ( | const Mat * | samples, |
| int | nsamples, | ||
| Mat & | covar, | ||
| Mat & | mean, | ||
| int | flags, | ||
| int | ctype = CV_64F |
||
| ) |
Calculates the covariance matrix of a set of vectors.
The functions calcCovarMatrix calculate the covariance matrix and, optionally, the mean vector of the set of input vectors.
| samples | samples stored as separate matrices |
| nsamples | number of samples |
| covar | output covariance matrix of the type ctype and square size. |
| mean | input or output (depending on the flags) array as the average value of the input vectors. |
| flags | operation flags as a combination of cv::CovarFlags |
| ctype | type of the matrixl; it equals 'CV_64F' by default. |
| void cv::calcCovarMatrix | ( | InputArray | samples, |
| OutputArray | covar, | ||
| InputOutputArray | mean, | ||
| int | flags, | ||
| int | ctype = CV_64F |
||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| samples | samples stored as rows/columns of a single matrix. |
| covar | output covariance matrix of the type ctype and square size. |
| mean | input or output (depending on the flags) array as the average value of the input vectors. |
| flags | operation flags as a combination of cv::CovarFlags |
| ctype | type of the matrixl; it equals 'CV_64F' by default. |
| void cv::cartToPolar | ( | InputArray | x, |
| InputArray | y, | ||
| OutputArray | magnitude, | ||
| OutputArray | angle, | ||
| bool | angleInDegrees = false |
||
| ) |
Calculates the magnitude and angle of 2D vectors.
The function cartToPolar calculates either the magnitude, angle, or both for every 2D vector (x(I),y(I)):
\[\begin{array}{l} \texttt{magnitude} (I)= \sqrt{\texttt{x}(I)^2+\texttt{y}(I)^2} , \\ \texttt{angle} (I)= \texttt{atan2} ( \texttt{y} (I), \texttt{x} (I))[ \cdot180 / \pi ] \end{array}\]
The angles are calculated with accuracy about 0.3 degrees. For the point (0,0), the angle is set to 0.
| x | array of x-coordinates; this must be a single-precision or double-precision floating-point array. |
| y | array of y-coordinates, that must have the same size and same type as x. |
| magnitude | output array of magnitudes of the same size and type as x. |
| angle | output array of angles that has the same size and type as x; the angles are measured in radians (from 0 to 2*Pi) or in degrees (0 to 360 degrees). |
| angleInDegrees | a flag, indicating whether the angles are measured in radians (which is by default), or in degrees. |
| bool cv::checkRange | ( | InputArray | a, |
| bool | quiet = true, |
||
| Point * | pos = 0, |
||
| double | minVal = -DBL_MAX, |
||
| double | maxVal = DBL_MAX |
||
| ) |
Checks every element of an input array for invalid values.
The functions checkRange check that every array element is neither NaN nor infinite. When minVal > -DBL_MAX and maxVal < DBL_MAX, the functions also check that each value is between minVal and maxVal. In case of multi-channel arrays, each channel is processed independently. If some values are out of range, position of the first outlier is stored in pos (when pos != NULL). Then, the functions either return false (when quiet=true) or throw an exception.
| a | input array. |
| quiet | a flag, indicating whether the functions quietly return false when the array elements are out of range or they throw an exception. |
| pos | optional output parameter, when not NULL, must be a pointer to array of src.dims elements. |
| minVal | inclusive lower boundary of valid values range. |
| maxVal | exclusive upper boundary of valid values range. |
| void cv::compare | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| int | cmpop | ||
| ) |
Performs the per-element comparison of two arrays or an array and scalar value.
The function compares: Elements of two arrays when src1 and src2 have the same size:
\[\texttt{dst} (I) = \texttt{src1} (I) \,\texttt{cmpop}\, \texttt{src2} (I)\]
Elements of src1 with a scalar src2 when src2 is constructed from Scalar or has a single element:
\[\texttt{dst} (I) = \texttt{src1}(I) \,\texttt{cmpop}\, \texttt{src2}\]
src1 with elements of src2 when src1 is constructed from Scalar or has a single element:
\[\texttt{dst} (I) = \texttt{src1} \,\texttt{cmpop}\, \texttt{src2} (I)\]
When the comparison result is true, the corresponding element of output array is set to 255. The comparison operations can be replaced with the equivalent matrix expressions:
| src1 | first input array or a scalar; when it is an array, it must have a single channel. |
| src2 | second input array or a scalar; when it is an array, it must have a single channel. |
| dst | output array of type ref CV_8U that has the same size and the same number of channels as the input arrays. |
| cmpop | a flag, that specifies correspondence between the arrays (cv::CmpTypes) |
| void cv::completeSymm | ( | InputOutputArray | mtx, |
| bool | lowerToUpper = false |
||
| ) |
Copies the lower or the upper half of a square matrix to another half.
The function completeSymm copies the lower half of a square matrix to its another half. The matrix diagonal remains unchanged: \(\texttt{mtx}_{ij}=\texttt{mtx}_{ji}\) for \(i > j\) if lowerToUpper=false \(\texttt{mtx}_{ij}=\texttt{mtx}_{ji}\) for \(i < j\) if lowerToUpper=true
| mtx | input-output floating-point square matrix. |
| lowerToUpper | operation flag; if true, the lower half is copied to the upper half. Otherwise, the upper half is copied to the lower half. |
| void cv::convertScaleAbs | ( | InputArray | src, |
| OutputArray | dst, | ||
| double | alpha = 1, |
||
| double | beta = 0 |
||
| ) |
Scales, calculates absolute values, and converts the result to 8-bit.
On each element of the input array, the function convertScaleAbs performs three operations sequentially: scaling, taking an absolute value, conversion to an unsigned 8-bit type:
\[\texttt{dst} (I)= \texttt{saturate\_cast<uchar>} (| \texttt{src} (I)* \texttt{alpha} + \texttt{beta} |)\]
In case of multi-channel arrays, the function processes each channel independently. When the output is not 8-bit, the operation can be emulated by calling the Mat::convertTo method (or by using matrix expressions) and then by calculating an absolute value of the result. For example:
| src | input array. |
| dst | output array. |
| alpha | optional scale factor. |
| beta | optional delta added to the scaled values. |
| void cv::copyMakeBorder | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | top, | ||
| int | bottom, | ||
| int | left, | ||
| int | right, | ||
| int | borderType, | ||
| const Scalar & | value = Scalar() |
||
| ) |
Forms a border around an image.
The function copies the source image into the middle of the destination image. The areas to the left, to the right, above and below the copied source image will be filled with extrapolated pixels. This is not what filtering functions based on it do (they extrapolate pixels on-fly), but what other more complex functions, including your own, may do to simplify image boundary handling.
The function supports the mode when src is already in the middle of dst . In this case, the function does not copy src itself but simply constructs the border, for example:
| src | Source image. |
| dst | Destination image of the same type as src and the size Size(src.cols+left+right, src.rows+top+bottom) . |
| top | |
| bottom | |
| left | |
| right | Parameter specifying how many pixels in each direction from the source image rectangle to extrapolate. For example, top=1, bottom=1, left=1, right=1 mean that 1 pixel-wide border needs to be built. |
| borderType | Border type. See borderInterpolate for details. |
| value | Border value if borderType==BORDER_CONSTANT . |
| int cv::countNonZero | ( | InputArray | src | ) |
Counts non-zero array elements.
The function returns the number of non-zero elements in src :
\[\sum _{I: \; \texttt{src} (I) \ne0 } 1\]
| src | single-channel array. |
| void cv::dct | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flags = 0 |
||
| ) |
Performs a forward or inverse discrete Cosine transform of 1D or 2D array.
The function dct performs a forward or inverse discrete Cosine transform (DCT) of a 1D or 2D floating-point array:
\[Y = C^{(N)} \cdot X\]
where\[C^{(N)}_{jk}= \sqrt{\alpha_j/N} \cos \left ( \frac{\pi(2k+1)j}{2N} \right )\]
and \(\alpha_0=1\), \(\alpha_j=2\) for j > 0.\[X = \left (C^{(N)} \right )^{-1} \cdot Y = \left (C^{(N)} \right )^T \cdot Y\]
(since \(C^{(N)}\) is an orthogonal matrix, \(C^{(N)} \cdot \left(C^{(N)}\right)^T = I\) )\[Y = C^{(N)} \cdot X \cdot \left (C^{(N)} \right )^T\]
\[X = \left (C^{(N)} \right )^T \cdot X \cdot C^{(N)}\]
The function chooses the mode of operation by looking at the flags and size of the input array:
| src | input floating-point array. |
| dst | output array of the same size and type as src . |
| flags | transformation flags as a combination of cv::DftFlags (DCT_*) |
| double cv::determinant | ( | InputArray | mtx | ) |
Returns the determinant of a square floating-point matrix.
The function determinant calculates and returns the determinant of the specified matrix. For small matrices ( mtx.cols=mtx.rows<=3 ), the direct method is used. For larger matrices, the function uses LU factorization with partial pivoting.
For symmetric positively-determined matrices, it is also possible to use eigen decomposition to calculate the determinant.
| mtx | input matrix that must have CV_32FC1 or CV_64FC1 type and square size. |
| void cv::dft | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flags = 0, |
||
| int | nonzeroRows = 0 |
||
| ) |
Performs a forward or inverse Discrete Fourier transform of a 1D or 2D floating-point array.
The function performs one of the following:
\[Y = F^{(N)} \cdot X,\]
where \(F^{(N)}_{jk}=\exp(-2\pi i j k/N)\) and \(i=\sqrt{-1}\)\[\begin{array}{l} X'= \left (F^{(N)} \right )^{-1} \cdot Y = \left (F^{(N)} \right )^* \cdot y \\ X = (1/N) \cdot X, \end{array}\]
where \(F^*=\left(\textrm{Re}(F^{(N)})-\textrm{Im}(F^{(N)})\right)^T\)\[Y = F^{(M)} \cdot X \cdot F^{(N)}\]
\[\begin{array}{l} X'= \left (F^{(M)} \right )^* \cdot Y \cdot \left (F^{(N)} \right )^* \\ X = \frac{1}{M \cdot N} \cdot X' \end{array}\]
In case of real (single-channel) data, the output spectrum of the forward Fourier transform or input spectrum of the inverse Fourier transform can be represented in a packed format called CCS (complex-conjugate-symmetrical). It was borrowed from IPL (Intel* Image Processing Library). Here is how 2D CCS spectrum looks:
\[\begin{bmatrix} Re Y_{0,0} & Re Y_{0,1} & Im Y_{0,1} & Re Y_{0,2} & Im Y_{0,2} & \cdots & Re Y_{0,N/2-1} & Im Y_{0,N/2-1} & Re Y_{0,N/2} \\ Re Y_{1,0} & Re Y_{1,1} & Im Y_{1,1} & Re Y_{1,2} & Im Y_{1,2} & \cdots & Re Y_{1,N/2-1} & Im Y_{1,N/2-1} & Re Y_{1,N/2} \\ Im Y_{1,0} & Re Y_{2,1} & Im Y_{2,1} & Re Y_{2,2} & Im Y_{2,2} & \cdots & Re Y_{2,N/2-1} & Im Y_{2,N/2-1} & Im Y_{1,N/2} \\ \hdotsfor{9} \\ Re Y_{M/2-1,0} & Re Y_{M-3,1} & Im Y_{M-3,1} & \hdotsfor{3} & Re Y_{M-3,N/2-1} & Im Y_{M-3,N/2-1}& Re Y_{M/2-1,N/2} \\ Im Y_{M/2-1,0} & Re Y_{M-2,1} & Im Y_{M-2,1} & \hdotsfor{3} & Re Y_{M-2,N/2-1} & Im Y_{M-2,N/2-1}& Im Y_{M/2-1,N/2} \\ Re Y_{M/2,0} & Re Y_{M-1,1} & Im Y_{M-1,1} & \hdotsfor{3} & Re Y_{M-1,N/2-1} & Im Y_{M-1,N/2-1}& Re Y_{M/2,N/2} \end{bmatrix}\]
In case of 1D transform of a real vector, the output looks like the first row of the matrix above.
So, the function chooses an operation mode depending on the flags and size of the input array:
If DFT_SCALE is set, the scaling is done after the transformation.
Unlike dct , the function supports arrays of arbitrary size. But only those arrays are processed efficiently, whose sizes can be factorized in a product of small prime numbers (2, 3, and 5 in the current implementation). Such an efficient DFT size can be calculated using the getOptimalDFTSize method.
The sample below illustrates how to calculate a DFT-based convolution of two 2D real arrays:
To optimize this sample, consider the following approaches:
All of the above improvements have been implemented in matchTemplate and filter2D . Therefore, by using them, you can get the performance even better than with the above theoretically optimal implementation. Though, those two functions actually calculate cross-correlation, not convolution, so you need to "flip" the second convolution operand B vertically and horizontally using flip .
| src | input array that could be real or complex. |
| dst | output array whose size and type depends on the flags . |
| flags | transformation flags, representing a combination of the cv::DftFlags |
| nonzeroRows | when the parameter is not zero, the function assumes that only the first nonzeroRows rows of the input array (DFT_INVERSE is not set) or only the first nonzeroRows of the output array (DFT_INVERSE is set) contain non-zeros, thus, the function can handle the rest of the rows more efficiently and save some time; this technique is very useful for calculating array cross-correlation or convolution using DFT. |
| void cv::divide | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| double | scale = 1, |
||
| int | dtype = -1 |
||
| ) |
Performs per-element division of two arrays or a scalar by an array.
The functions divide divide one array by another:
\[\texttt{dst(I) = saturate(src1(I)*scale/src2(I))}\]
or a scalar by an array when there is no src1 :
\[\texttt{dst(I) = saturate(scale/src2(I))}\]
When src2(I) is zero, dst(I) will also be zero. Different channels of multi-channel arrays are processed independently.
| src1 | first input array. |
| src2 | second input array of the same size and type as src1. |
| scale | scalar factor. |
| dst | output array of the same size and type as src2. |
| dtype | optional depth of the output array; if -1, dst will have depth src2.depth(), but in case of an array-by-array division, you can only pass -1 when src1.depth()==src2.depth(). |
| void cv::divide | ( | double | scale, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| int | dtype = -1 |
||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| bool cv::eigen | ( | InputArray | src, |
| OutputArray | eigenvalues, | ||
| OutputArray | eigenvectors = noArray() |
||
| ) |
Calculates eigenvalues and eigenvectors of a symmetric matrix.
The functions eigen calculate just eigenvalues, or eigenvalues and eigenvectors of the symmetric matrix src:
| src | input matrix that must have CV_32FC1 or CV_64FC1 type, square size and be symmetrical (src ^T^ == src). |
| eigenvalues | output vector of eigenvalues of the same type as src; the eigenvalues are stored in the descending order. |
| eigenvectors | output matrix of eigenvectors; it has the same size and type as src; the eigenvectors are stored as subsequent matrix rows, in the same order as the corresponding eigenvalues. |
| void cv::exp | ( | InputArray | src, |
| OutputArray | dst | ||
| ) |
Calculates the exponent of every array element.
The function exp calculates the exponent of every element of the input array:
\[\texttt{dst} [I] = e^{ src(I) }\]
The maximum relative error is about 7e-6 for single-precision input and less than 1e-10 for double-precision input. Currently, the function converts denormalized values to zeros on output. Special values (NaN, Inf) are not handled.
| src | input array. |
| dst | output array of the same size and type as src. |
| void cv::extractChannel | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | coi | ||
| ) |
extracts a single channel from src (coi is 0-based index)
| void cv::findNonZero | ( | InputArray | src, |
| OutputArray | idx | ||
| ) |
Returns the list of locations of non-zero pixels.
Given a binary matrix (likely returned from an operation such as threshold(), compare(), >, ==, etc, return all of the non-zero indices as a cv::Mat or std::vector<cv::Point> (x,y) For example:
or
| src | single-channel array (type CV_8UC1) |
| idx | the output array, type of cv::Mat or std::vector<Point>, corresponding to non-zero indices in the input |
| void cv::flip | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flipCode | ||
| ) |
Flips a 2D array around vertical, horizontal, or both axes.
The function flip flips the array in one of three different ways (row and column indices are 0-based):
\[\texttt{dst} _{ij} = \left\{ \begin{array}{l l} \texttt{src} _{\texttt{src.rows}-i-1,j} & if\; \texttt{flipCode} = 0 \\ \texttt{src} _{i, \texttt{src.cols} -j-1} & if\; \texttt{flipCode} > 0 \\ \texttt{src} _{ \texttt{src.rows} -i-1, \texttt{src.cols} -j-1} & if\; \texttt{flipCode} < 0 \\ \end{array} \right.\]
The example scenarios of using the function are the following: Vertical flipping of the image (flipCode == 0) to switch between top-left and bottom-left image origin. This is a typical operation in video processing on Microsoft Windows* OS. Horizontal flipping of the image with the subsequent horizontal shift and absolute difference calculation to check for a vertical-axis symmetry (flipCode > 0). Simultaneous horizontal and vertical flipping of the image with the subsequent shift and absolute difference calculation to check for a central symmetry (flipCode < 0). Reversing the order of point arrays (flipCode > 0 or flipCode == 0).
| src | input array. |
| dst | output array of the same size and type as src. |
| flipCode | a flag to specify how to flip the array; 0 means flipping around the x-axis and positive value (for example, 1) means flipping around y-axis. Negative value (for example, -1) means flipping around both axes. |
| void cv::gemm | ( | InputArray | src1, |
| InputArray | src2, | ||
| double | alpha, | ||
| InputArray | src3, | ||
| double | beta, | ||
| OutputArray | dst, | ||
| int | flags = 0 |
||
| ) |
Performs generalized matrix multiplication.
The function performs generalized matrix multiplication similar to the gemm functions in BLAS level 3. For example, gemm(src1, src2, alpha, src3, beta, dst, GEMM_1_T + GEMM_3_T) corresponds to
\[\texttt{dst} = \texttt{alpha} \cdot \texttt{src1} ^T \cdot \texttt{src2} + \texttt{beta} \cdot \texttt{src3} ^T\]
In case of complex (two-channel) data, performed a complex matrix multiplication.
The function can be replaced with a matrix expression. For example, the above call can be replaced with:
| src1 | first multiplied input matrix that could be real(CV_32FC1, CV_64FC1) or complex(CV_32FC2, CV_64FC2). |
| src2 | second multiplied input matrix of the same type as src1. |
| alpha | weight of the matrix product. |
| src3 | third optional delta matrix added to the matrix product; it should have the same type as src1 and src2. |
| beta | weight of src3. |
| dst | output matrix; it has the proper size and the same type as input matrices. |
| flags | operation flags (cv::GemmFlags) |
| int cv::getOptimalDFTSize | ( | int | vecsize | ) |
Returns the optimal DFT size for a given vector size.
DFT performance is not a monotonic function of a vector size. Therefore, when you calculate convolution of two arrays or perform the spectral analysis of an array, it usually makes sense to pad the input data with zeros to get a bit larger array that can be transformed much faster than the original one. Arrays whose size is a power-of-two (2, 4, 8, 16, 32, ...) are the fastest to process. Though, the arrays whose size is a product of 2's, 3's, and 5's (for example, 300 = 5*5*3*2*2) are also processed quite efficiently.
The function getOptimalDFTSize returns the minimum number N that is greater than or equal to vecsize so that the DFT of a vector of size N can be processed efficiently. In the current implementation N = 2 ^p^ * 3 ^q^ * 5 ^r^ for some integer p, q, r.
The function returns a negative number if vecsize is too large (very close to INT_MAX ).
While the function cannot be used directly to estimate the optimal vector size for DCT transform (since the current DCT implementation supports only even-size vectors), it can be easily processed as getOptimalDFTSize((vecsize+1)/2)*2.
| vecsize | vector size. |
| void cv::hconcat | ( | const Mat * | src, |
| size_t | nsrc, | ||
| OutputArray | dst | ||
| ) |
Applies horizontal concatenation to given matrices.
The function horizontally concatenates two or more cv::Mat matrices (with the same number of rows).
| src | input array or vector of matrices. all of the matrices must have the same number of rows and the same depth. |
| nsrc | number of matrices in src. |
| dst | output array. It has the same number of rows and depth as the src, and the sum of cols of the src. |
| void cv::hconcat | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src1 | first input array to be considered for horizontal concatenation. |
| src2 | second input array to be considered for horizontal concatenation. |
| dst | output array. It has the same number of rows and depth as the src1 and src2, and the sum of cols of the src1 and src2. |
| void cv::hconcat | ( | InputArrayOfArrays | src, |
| OutputArray | dst | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src | input array or vector of matrices. all of the matrices must have the same number of rows and the same depth. |
| dst | output array. It has the same number of rows and depth as the src, and the sum of cols of the src. same depth. |
| void cv::idct | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flags = 0 |
||
| ) |
Calculates the inverse Discrete Cosine Transform of a 1D or 2D array.
idct(src, dst, flags) is equivalent to dct(src, dst, flags | DCT_INVERSE).
| src | input floating-point single-channel array. |
| dst | output array of the same size and type as src. |
| flags | operation flags. |
| void cv::idft | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flags = 0, |
||
| int | nonzeroRows = 0 |
||
| ) |
Calculates the inverse Discrete Fourier Transform of a 1D or 2D array.
idft(src, dst, flags) is equivalent to dft(src, dst, flags | DFT_INVERSE) .
| src | input floating-point real or complex array. |
| dst | output array whose size and type depend on the flags. |
| flags | operation flags (see dft and cv::DftFlags). |
| nonzeroRows | number of dst rows to process; the rest of the rows have undefined content (see the convolution sample in dft description. |
| void cv::inRange | ( | InputArray | src, |
| InputArray | lowerb, | ||
| InputArray | upperb, | ||
| OutputArray | dst | ||
| ) |
Checks if array elements lie between the elements of two other arrays.
The function checks the range as follows:
\[\texttt{dst} (I)= \texttt{lowerb} (I)_0 \leq \texttt{src} (I)_0 \leq \texttt{upperb} (I)_0\]
\[\texttt{dst} (I)= \texttt{lowerb} (I)_0 \leq \texttt{src} (I)_0 \leq \texttt{upperb} (I)_0 \land \texttt{lowerb} (I)_1 \leq \texttt{src} (I)_1 \leq \texttt{upperb} (I)_1\]
That is, dst (I) is set to 255 (all 1 -bits) if src (I) is within the specified 1D, 2D, 3D, ... box and 0 otherwise.
When the lower and/or upper boundary parameters are scalars, the indexes (I) at lowerb and upperb in the above formulas should be omitted.
| src | first input array. |
| lowerb | inclusive lower boundary array or a scalar. |
| upperb | inclusive upper boundary array or a scalar. |
| dst | output array of the same size as src and CV_8U type. |
| void cv::insertChannel | ( | InputArray | src, |
| InputOutputArray | dst, | ||
| int | coi | ||
| ) |
inserts a single channel to dst (coi is 0-based index)
| double cv::invert | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flags = DECOMP_LU |
||
| ) |
Finds the inverse or pseudo-inverse of a matrix.
The function invert inverts the matrix src and stores the result in dst . When the matrix src is singular or non-square, the function calculates the pseudo-inverse matrix (the dst matrix) so that norm(src*dst - I) is minimal, where I is an identity matrix.
In case of the DECOMP_LU method, the function returns non-zero value if the inverse has been successfully calculated and 0 if src is singular.
In case of the DECOMP_SVD method, the function returns the inverse condition number of src (the ratio of the smallest singular value to the largest singular value) and 0 if src is singular. The SVD method calculates a pseudo-inverse matrix if src is singular.
Similarly to DECOMP_LU, the method DECOMP_CHOLESKY works only with non-singular square matrices that should also be symmetrical and positively defined. In this case, the function stores the inverted matrix in dst and returns non-zero. Otherwise, it returns 0.
| src | input floating-point M x N matrix. |
| dst | output matrix of N x M size and the same type as src. |
| flags | inversion method (cv::DecompTypes) |
| void cv::log | ( | InputArray | src, |
| OutputArray | dst | ||
| ) |
Calculates the natural logarithm of every array element.
The function log calculates the natural logarithm of the absolute value of every element of the input array:
\[\texttt{dst} (I) = \fork{\log |\texttt{src}(I)|}{if \(\texttt{src}(I) \ne 0\) }{\texttt{C}}{otherwise}\]
where C is a large negative number (about -700 in the current implementation). The maximum relative error is about 7e-6 for single-precision input and less than 1e-10 for double-precision input. Special values (NaN, Inf) are not handled.
| src | input array. |
| dst | output array of the same size and type as src . |
| void cv::LUT | ( | InputArray | src, |
| InputArray | lut, | ||
| OutputArray | dst | ||
| ) |
Performs a look-up table transform of an array.
The function LUT fills the output array with values from the look-up table. Indices of the entries are taken from the input array. That is, the function processes each element of src as follows:
\[\texttt{dst} (I) \leftarrow \texttt{lut(src(I) + d)}\]
where
\[d = \fork{0}{if \(\texttt{src}\) has depth \(\texttt{CV_8U}\)}{128}{if \(\texttt{src}\) has depth \(\texttt{CV_8S}\)}\]
| src | input array of 8-bit elements. |
| lut | look-up table of 256 elements; in case of multi-channel input array, the table should either have a single channel (in this case the same table is used for all channels) or the same number of channels as in the input array. |
| dst | output array of the same size and number of channels as src, and the same depth as lut. |
| void cv::magnitude | ( | InputArray | x, |
| InputArray | y, | ||
| OutputArray | magnitude | ||
| ) |
Calculates the magnitude of 2D vectors.
The function magnitude calculates the magnitude of 2D vectors formed from the corresponding elements of x and y arrays:
\[\texttt{dst} (I) = \sqrt{\texttt{x}(I)^2 + \texttt{y}(I)^2}\]
| x | floating-point array of x-coordinates of the vectors. |
| y | floating-point array of y-coordinates of the vectors; it must have the same size as x. |
| magnitude | output array of the same size and type as x. |
| double cv::Mahalanobis | ( | InputArray | v1, |
| InputArray | v2, | ||
| InputArray | icovar | ||
| ) |
Calculates the Mahalanobis distance between two vectors.
The function Mahalanobis calculates and returns the weighted distance between two vectors:
\[d( \texttt{vec1} , \texttt{vec2} )= \sqrt{\sum_{i,j}{\texttt{icovar(i,j)}\cdot(\texttt{vec1}(I)-\texttt{vec2}(I))\cdot(\texttt{vec1(j)}-\texttt{vec2(j)})} }\]
The covariance matrix may be calculated using the cv::calcCovarMatrix function and then inverted using the invert function (preferably using the cv::DECOMP_SVD method, as the most accurate).
| v1 | first 1D input vector. |
| v2 | second 1D input vector. |
| icovar | inverse covariance matrix. |
| void cv::max | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst | ||
| ) |
Calculates per-element maximum of two arrays or an array and a scalar.
The functions max calculate the per-element maximum of two arrays:
\[\texttt{dst} (I)= \max ( \texttt{src1} (I), \texttt{src2} (I))\]
or array and a scalar:
\[\texttt{dst} (I)= \max ( \texttt{src1} (I), \texttt{value} )\]
| src1 | first input array. |
| src2 | second input array of the same size and type as src1 . |
| dst | output array of the same size and type as src1. |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. needed to avoid conflicts with const _Tp& std::min(const _Tp&, const _Tp&, _Compare)
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. needed to avoid conflicts with const _Tp& std::min(const _Tp&, const _Tp&, _Compare)
| Scalar cv::mean | ( | InputArray | src, |
| InputArray | mask = noArray() |
||
| ) |
Calculates an average (mean) of array elements.
The function mean calculates the mean value M of array elements, independently for each channel, and return it:
\[\begin{array}{l} N = \sum _{I: \; \texttt{mask} (I) \ne 0} 1 \\ M_c = \left ( \sum _{I: \; \texttt{mask} (I) \ne 0}{ \texttt{mtx} (I)_c} \right )/N \end{array}\]
When all the mask elements are 0's, the functions return Scalar::all(0)
| src | input array that should have from 1 to 4 channels so that the result can be stored in Scalar_ . |
| mask | optional operation mask. |
| void cv::meanStdDev | ( | InputArray | src, |
| OutputArray | mean, | ||
| OutputArray | stddev, | ||
| InputArray | mask = noArray() |
||
| ) |
Calculates a mean and standard deviation of array elements.
The function meanStdDev calculates the mean and the standard deviation M of array elements independently for each channel and returns it via the output parameters:
\[\begin{array}{l} N = \sum _{I, \texttt{mask} (I) \ne 0} 1 \\ \texttt{mean} _c = \frac{\sum_{ I: \; \texttt{mask}(I) \ne 0} \texttt{src} (I)_c}{N} \\ \texttt{stddev} _c = \sqrt{\frac{\sum_{ I: \; \texttt{mask}(I) \ne 0} \left ( \texttt{src} (I)_c - \texttt{mean} _c \right )^2}{N}} \end{array}\]
When all the mask elements are 0's, the functions return mean=stddev=Scalar::all(0).
| src | input array that should have from 1 to 4 channels so that the results can be stored in Scalar_ 's. |
| mean | output parameter: calculated mean value. |
| stddev | output parameter: calculateded standard deviation. |
| mask | optional operation mask. |
| void cv::merge | ( | const Mat * | mv, |
| size_t | count, | ||
| OutputArray | dst | ||
| ) |
Creates one multichannel array out of several single-channel ones.
The functions merge merge several arrays to make a single multi-channel array. That is, each element of the output array will be a concatenation of the elements of the input arrays, where elements of i-th input array are treated as mv[i].channels()-element vectors.
The function split does the reverse operation. If you need to shuffle channels in some other advanced way, use mixChannels .
| mv | input array of matrices to be merged; all the matrices in mv must have the same size and the same depth. |
| count | number of input matrices when mv is a plain C array; it must be greater than zero. |
| dst | output array of the same size and the same depth as mv[0]; The number of channels will be the total number of channels in the matrix array. |
| void cv::merge | ( | InputArrayOfArrays | mv, |
| OutputArray | dst | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| mv | input vector of matrices to be merged; all the matrices in mv must have the same size and the same depth. |
| dst | output array of the same size and the same depth as mv[0]; The number of channels will be the total number of channels in the matrix array. |
| void cv::min | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst | ||
| ) |
Calculates per-element minimum of two arrays or an array and a scalar.
The functions min calculate the per-element minimum of two arrays:
\[\texttt{dst} (I)= \min ( \texttt{src1} (I), \texttt{src2} (I))\]
or array and a scalar:
\[\texttt{dst} (I)= \min ( \texttt{src1} (I), \texttt{value} )\]
| src1 | first input array. |
| src2 | second input array of the same size and type as src1. |
| dst | output array of the same size and type as src1. |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. needed to avoid conflicts with const _Tp& std::min(const _Tp&, const _Tp&, _Compare)
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts. needed to avoid conflicts with const _Tp& std::min(const _Tp&, const _Tp&, _Compare)
| void cv::minMaxIdx | ( | InputArray | src, |
| double * | minVal, | ||
| double * | maxVal = 0, |
||
| int * | minIdx = 0, |
||
| int * | maxIdx = 0, |
||
| InputArray | mask = noArray() |
||
| ) |
Finds the global minimum and maximum in an array.
The function minMaxIdx finds the minimum and maximum element values and their positions. The extremums are searched across the whole array or, if mask is not an empty array, in the specified array region. The function does not work with multi-channel arrays. If you need to find minimum or maximum elements across all the channels, use Mat::reshape first to reinterpret the array as single-channel. Or you may extract the particular channel using either extractImageCOI , or mixChannels , or split . In case of a sparse matrix, the minimum is found among non-zero elements only.
| src | input single-channel array. |
| minVal | pointer to the returned minimum value; NULL is used if not required. |
| maxVal | pointer to the returned maximum value; NULL is used if not required. |
| minIdx | pointer to the returned minimum location (in nD case); NULL is used if not required; Otherwise, it must point to an array of src.dims elements, the coordinates of the minimum element in each dimension are stored there sequentially. |
| maxIdx | pointer to the returned maximum location (in nD case). NULL is used if not required. |
| mask | specified array region |
| void cv::minMaxLoc | ( | InputArray | src, |
| double * | minVal, | ||
| double * | maxVal = 0, |
||
| Point * | minLoc = 0, |
||
| Point * | maxLoc = 0, |
||
| InputArray | mask = noArray() |
||
| ) |
Finds the global minimum and maximum in an array.
The functions minMaxLoc find the minimum and maximum element values and their positions. The extremums are searched across the whole array or, if mask is not an empty array, in the specified array region.
The functions do not work with multi-channel arrays. If you need to find minimum or maximum elements across all the channels, use Mat::reshape first to reinterpret the array as single-channel. Or you may extract the particular channel using either extractImageCOI , or mixChannels , or split .
| src | input single-channel array. |
| minVal | pointer to the returned minimum value; NULL is used if not required. |
| maxVal | pointer to the returned maximum value; NULL is used if not required. |
| minLoc | pointer to the returned minimum location (in 2D case); NULL is used if not required. |
| maxLoc | pointer to the returned maximum location (in 2D case); NULL is used if not required. |
| mask | optional mask used to select a sub-array. |
| void cv::minMaxLoc | ( | const SparseMat & | a, |
| double * | minVal, | ||
| double * | maxVal, | ||
| int * | minIdx = 0, |
||
| int * | maxIdx = 0 |
||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| a | input single-channel array. |
| minVal | pointer to the returned minimum value; NULL is used if not required. |
| maxVal | pointer to the returned maximum value; NULL is used if not required. |
| minIdx | pointer to the returned minimum location (in nD case); NULL is used if not required; Otherwise, it must point to an array of src.dims elements, the coordinates of the minimum element in each dimension are stored there sequentially. |
| maxIdx | pointer to the returned maximum location (in nD case). NULL is used if not required. |
| void cv::mixChannels | ( | const Mat * | src, |
| size_t | nsrcs, | ||
| Mat * | dst, | ||
| size_t | ndsts, | ||
| const int * | fromTo, | ||
| size_t | npairs | ||
| ) |
Copies specified channels from input arrays to the specified channels of output arrays.
The function cv::mixChannels provides an advanced mechanism for shuffling image channels.
cv::split and cv::merge and some forms of cv::cvtColor are partial cases of cv::mixChannels .
In the example below, the code splits a 4-channel BGRA image into a 3-channel BGR (with B and R channels swapped) and a separate alpha-channel image:
| src | input array or vector of matrices; all of the matrices must have the same size and the same depth. |
| nsrcs | number of matrices in src. |
| dst | output array or vector of matrices; all the matrices must be allocated; their size and depth must be the same as in src[0]. |
| ndsts | number of matrices in dst. |
| fromTo | array of index pairs specifying which channels are copied and where; fromTo[k*2] is a 0-based index of the input channel in src, fromTo[k*2+1] is an index of the output channel in dst; the continuous channel numbering is used: the first input image channels are indexed from 0 to src[0].channels()-1, the second input image channels are indexed from src[0].channels() to src[0].channels() + src[1].channels()-1, and so on, the same scheme is used for the output image channels; as a special case, when fromTo[k*2] is negative, the corresponding output channel is filled with zero . |
| npairs | number of index pairs in fromTo. |
| void cv::mixChannels | ( | InputArrayOfArrays | src, |
| InputOutputArrayOfArrays | dst, | ||
| const int * | fromTo, | ||
| size_t | npairs | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src | input array or vector of matrices; all of the matrices must have the same size and the same depth. |
| dst | output array or vector of matrices; all the matrices must be allocated; their size and depth must be the same as in src[0]. |
| fromTo | array of index pairs specifying which channels are copied and where; fromTo[k*2] is a 0-based index of the input channel in src, fromTo[k*2+1] is an index of the output channel in dst; the continuous channel numbering is used: the first input image channels are indexed from 0 to src[0].channels()-1, the second input image channels are indexed from src[0].channels() to src[0].channels() + src[1].channels()-1, and so on, the same scheme is used for the output image channels; as a special case, when fromTo[k*2] is negative, the corresponding output channel is filled with zero . |
| npairs | number of index pairs in fromTo. |
| void cv::mixChannels | ( | InputArrayOfArrays | src, |
| InputOutputArrayOfArrays | dst, | ||
| const std::vector< int > & | fromTo | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src | input array or vector of matrices; all of the matrices must have the same size and the same depth. |
| dst | output array or vector of matrices; all the matrices must be allocated; their size and depth must be the same as in src[0]. |
| fromTo | array of index pairs specifying which channels are copied and where; fromTo[k*2] is a 0-based index of the input channel in src, fromTo[k*2+1] is an index of the output channel in dst; the continuous channel numbering is used: the first input image channels are indexed from 0 to src[0].channels()-1, the second input image channels are indexed from src[0].channels() to src[0].channels() + src[1].channels()-1, and so on, the same scheme is used for the output image channels; as a special case, when fromTo[k*2] is negative, the corresponding output channel is filled with zero . |
| void cv::mulSpectrums | ( | InputArray | a, |
| InputArray | b, | ||
| OutputArray | c, | ||
| int | flags, | ||
| bool | conjB = false |
||
| ) |
Performs the per-element multiplication of two Fourier spectrums.
The function mulSpectrums performs the per-element multiplication of the two CCS-packed or complex matrices that are results of a real or complex Fourier transform.
The function, together with dft and idft , may be used to calculate convolution (pass conjB=false ) or correlation (pass conjB=true ) of two arrays rapidly. When the arrays are complex, they are simply multiplied (per element) with an optional conjugation of the second-array elements. When the arrays are real, they are assumed to be CCS-packed (see dft for details).
| a | first input array. |
| b | second input array of the same size and type as src1 . |
| c | output array of the same size and type as src1 . |
| flags | operation flags; currently, the only supported flag is cv::DFT_ROWS, which indicates that each row of src1 and src2 is an independent 1D Fourier spectrum. If you do not want to use this flag, then simply add a 0 as value. |
| conjB | optional flag that conjugates the second input array before the multiplication (true) or not (false). |
| void cv::multiply | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| double | scale = 1, |
||
| int | dtype = -1 |
||
| ) |
Calculates the per-element scaled product of two arrays.
The function multiply calculates the per-element product of two arrays:
\[\texttt{dst} (I)= \texttt{saturate} ( \texttt{scale} \cdot \texttt{src1} (I) \cdot \texttt{src2} (I))\]
There is also a MatrixExpressions -friendly variant of the first function. See Mat::mul .
For a not-per-element matrix product, see gemm .
| src1 | first input array. |
| src2 | second input array of the same size and the same type as src1. |
| dst | output array of the same size and type as src1. |
| scale | optional scale factor. |
| dtype | optional depth of the output array |
| void cv::mulTransposed | ( | InputArray | src, |
| OutputArray | dst, | ||
| bool | aTa, | ||
| InputArray | delta = noArray(), |
||
| double | scale = 1, |
||
| int | dtype = -1 |
||
| ) |
Calculates the product of a matrix and its transposition.
The function mulTransposed calculates the product of src and its transposition:
\[\texttt{dst} = \texttt{scale} ( \texttt{src} - \texttt{delta} )^T ( \texttt{src} - \texttt{delta} )\]
if aTa=true , and
\[\texttt{dst} = \texttt{scale} ( \texttt{src} - \texttt{delta} ) ( \texttt{src} - \texttt{delta} )^T\]
otherwise. The function is used to calculate the covariance matrix. With zero delta, it can be used as a faster substitute for general matrix product A*B when B=A'
| src | input single-channel matrix. Note that unlike gemm, the function can multiply not only floating-point matrices. |
| dst | output square matrix. |
| aTa | Flag specifying the multiplication ordering. See the description below. |
| delta | Optional delta matrix subtracted from src before the multiplication. When the matrix is empty ( delta=noArray() ), it is assumed to be zero, that is, nothing is subtracted. If it has the same size as src , it is simply subtracted. Otherwise, it is "repeated" (see repeat ) to cover the full src and then subtracted. Type of the delta matrix, when it is not empty, must be the same as the type of created output matrix. See the dtype parameter description below. |
| scale | Optional scale factor for the matrix product. |
| dtype | Optional type of the output matrix. When it is negative, the output matrix will have the same type as src . Otherwise, it will be type=CV_MAT_DEPTH(dtype) that should be either CV_32F or CV_64F . |
| double cv::norm | ( | InputArray | src1, |
| int | normType = NORM_L2, |
||
| InputArray | mask = noArray() |
||
| ) |
Calculates an absolute array norm, an absolute difference norm, or a relative difference norm.
The functions norm calculate an absolute norm of src1 (when there is no src2 ):
\[norm = \forkthree{\|\texttt{src1}\|_{L_{\infty}} = \max _I | \texttt{src1} (I)|}{if \(\texttt{normType} = \texttt{NORM_INF}\) } { \| \texttt{src1} \| _{L_1} = \sum _I | \texttt{src1} (I)|}{if \(\texttt{normType} = \texttt{NORM_L1}\) } { \| \texttt{src1} \| _{L_2} = \sqrt{\sum_I \texttt{src1}(I)^2} }{if \(\texttt{normType} = \texttt{NORM_L2}\) }\]
or an absolute or relative difference norm if src2 is there:
\[norm = \forkthree{\|\texttt{src1}-\texttt{src2}\|_{L_{\infty}} = \max _I | \texttt{src1} (I) - \texttt{src2} (I)|}{if \(\texttt{normType} = \texttt{NORM_INF}\) } { \| \texttt{src1} - \texttt{src2} \| _{L_1} = \sum _I | \texttt{src1} (I) - \texttt{src2} (I)|}{if \(\texttt{normType} = \texttt{NORM_L1}\) } { \| \texttt{src1} - \texttt{src2} \| _{L_2} = \sqrt{\sum_I (\texttt{src1}(I) - \texttt{src2}(I))^2} }{if \(\texttt{normType} = \texttt{NORM_L2}\) }\]
or
\[norm = \forkthree{\frac{\|\texttt{src1}-\texttt{src2}\|_{L_{\infty}} }{\|\texttt{src2}\|_{L_{\infty}} }}{if \(\texttt{normType} = \texttt{NORM_RELATIVE_INF}\) } { \frac{\|\texttt{src1}-\texttt{src2}\|_{L_1} }{\|\texttt{src2}\|_{L_1}} }{if \(\texttt{normType} = \texttt{NORM_RELATIVE_L1}\) } { \frac{\|\texttt{src1}-\texttt{src2}\|_{L_2} }{\|\texttt{src2}\|_{L_2}} }{if \(\texttt{normType} = \texttt{NORM_RELATIVE_L2}\) }\]
The functions norm return the calculated norm.
When the mask parameter is specified and it is not empty, the norm is calculated only over the region specified by the mask.
A multi-channel input arrays are treated as a single-channel, that is, the results for all channels are combined.
| src1 | first input array. |
| normType | type of the norm (see cv::NormTypes). |
| mask | optional operation mask; it must have the same size as src1 and CV_8UC1 type. |
| double cv::norm | ( | InputArray | src1, |
| InputArray | src2, | ||
| int | normType = NORM_L2, |
||
| InputArray | mask = noArray() |
||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src1 | first input array. |
| src2 | second input array of the same size and the same type as src1. |
| normType | type of the norm (cv::NormTypes). |
| mask | optional operation mask; it must have the same size as src1 and CV_8UC1 type. |
| double cv::norm | ( | const SparseMat & | src, |
| int | normType | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src | first input array. |
| normType | type of the norm (see cv::NormTypes). |
| void cv::normalize | ( | InputArray | src, |
| InputOutputArray | dst, | ||
| double | alpha = 1, |
||
| double | beta = 0, |
||
| int | norm_type = NORM_L2, |
||
| int | dtype = -1, |
||
| InputArray | mask = noArray() |
||
| ) |
Normalizes the norm or value range of an array.
The functions normalize scale and shift the input array elements so that
\[\| \texttt{dst} \| _{L_p}= \texttt{alpha}\]
(where p=Inf, 1 or 2) when normType=NORM_INF, NORM_L1, or NORM_L2, respectively; or so that
\[\min _I \texttt{dst} (I)= \texttt{alpha} , \, \, \max _I \texttt{dst} (I)= \texttt{beta}\]
when normType=NORM_MINMAX (for dense arrays only). The optional mask specifies a sub-array to be normalized. This means that the norm or min-n-max are calculated over the sub-array, and then this sub-array is modified to be normalized. If you want to only use the mask to calculate the norm or min-max but modify the whole array, you can use norm and Mat::convertTo.
In case of sparse matrices, only the non-zero values are analyzed and transformed. Because of this, the range transformation for sparse matrices is not allowed since it can shift the zero level.
Possible usage with some positive example data:
| src | input array. |
| dst | output array of the same size as src . |
| alpha | norm value to normalize to or the lower range boundary in case of the range normalization. |
| beta | upper range boundary in case of the range normalization; it is not used for the norm normalization. |
| norm_type | normalization type (see cv::NormTypes). |
| dtype | when negative, the output array has the same type as src; otherwise, it has the same number of channels as src and the depth =CV_MAT_DEPTH(dtype). |
| mask | optional operation mask. |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src | input array. |
| dst | output array of the same size as src . |
| alpha | norm value to normalize to or the lower range boundary in case of the range normalization. |
| normType | normalization type (see cv::NormTypes). |
| void cv::patchNaNs | ( | InputOutputArray | a, |
| double | val = 0 |
||
| ) |
converts NaN's to the given number
| void cv::PCABackProject | ( | InputArray | data, |
| InputArray | mean, | ||
| InputArray | eigenvectors, | ||
| OutputArray | result | ||
| ) |
wrap PCA::backProject
| void cv::PCACompute | ( | InputArray | data, |
| InputOutputArray | mean, | ||
| OutputArray | eigenvectors, | ||
| int | maxComponents = 0 |
||
| ) |
wrap PCA::operator()
| void cv::PCACompute | ( | InputArray | data, |
| InputOutputArray | mean, | ||
| OutputArray | eigenvectors, | ||
| double | retainedVariance | ||
| ) |
wrap PCA::operator()
| void cv::PCAProject | ( | InputArray | data, |
| InputArray | mean, | ||
| InputArray | eigenvectors, | ||
| OutputArray | result | ||
| ) |
wrap PCA::project
| void cv::perspectiveTransform | ( | InputArray | src, |
| OutputArray | dst, | ||
| InputArray | m | ||
| ) |
Performs the perspective matrix transformation of vectors.
The function perspectiveTransform transforms every element of src by treating it as a 2D or 3D vector, in the following way:
\[(x, y, z) \rightarrow (x'/w, y'/w, z'/w)\]
where
\[(x', y', z', w') = \texttt{mat} \cdot \begin{bmatrix} x & y & z & 1 \end{bmatrix}\]
and
\[w = \fork{w'}{if \(w' \ne 0\)}{\infty}{otherwise}\]
Here a 3D vector transformation is shown. In case of a 2D vector transformation, the z component is omitted.
| src | input two-channel or three-channel floating-point array; each element is a 2D/3D vector to be transformed. |
| dst | output array of the same size and type as src. |
| m | 3x3 or 4x4 floating-point transformation matrix. |
| void cv::phase | ( | InputArray | x, |
| InputArray | y, | ||
| OutputArray | angle, | ||
| bool | angleInDegrees = false |
||
| ) |
Calculates the rotation angle of 2D vectors.
The function phase calculates the rotation angle of each 2D vector that is formed from the corresponding elements of x and y :
\[\texttt{angle} (I) = \texttt{atan2} ( \texttt{y} (I), \texttt{x} (I))\]
The angle estimation accuracy is about 0.3 degrees. When x(I)=y(I)=0 , the corresponding angle(I) is set to 0.
| x | input floating-point array of x-coordinates of 2D vectors. |
| y | input array of y-coordinates of 2D vectors; it must have the same size and the same type as x. |
| angle | output array of vector angles; it has the same size and same type as x . |
| angleInDegrees | when true, the function calculates the angle in degrees, otherwise, they are measured in radians. |
| void cv::polarToCart | ( | InputArray | magnitude, |
| InputArray | angle, | ||
| OutputArray | x, | ||
| OutputArray | y, | ||
| bool | angleInDegrees = false |
||
| ) |
Calculates x and y coordinates of 2D vectors from their magnitude and angle.
The function polarToCart calculates the Cartesian coordinates of each 2D vector represented by the corresponding elements of magnitude and angle:
\[\begin{array}{l} \texttt{x} (I) = \texttt{magnitude} (I) \cos ( \texttt{angle} (I)) \\ \texttt{y} (I) = \texttt{magnitude} (I) \sin ( \texttt{angle} (I)) \\ \end{array}\]
The relative accuracy of the estimated coordinates is about 1e-6.
| magnitude | input floating-point array of magnitudes of 2D vectors; it can be an empty matrix (=Mat()), in this case, the function assumes that all the magnitudes are =1; if it is not empty, it must have the same size and type as angle. |
| angle | input floating-point array of angles of 2D vectors. |
| x | output array of x-coordinates of 2D vectors; it has the same size and type as angle. |
| y | output array of y-coordinates of 2D vectors; it has the same size and type as angle. |
| angleInDegrees | when true, the input angles are measured in degrees, otherwise, they are measured in radians. |
| void cv::pow | ( | InputArray | src, |
| double | power, | ||
| OutputArray | dst | ||
| ) |
Raises every array element to a power.
The function pow raises every element of the input array to power :
\[\texttt{dst} (I) = \fork{\texttt{src}(I)^{power}}{if \(\texttt{power}\) is integer}{|\texttt{src}(I)|^{power}}{otherwise}\]
So, for a non-integer power exponent, the absolute values of input array elements are used. However, it is possible to get true values for negative values using some extra operations. In the example below, computing the 5th root of array src shows:
For some values of power, such as integer values, 0.5 and -0.5, specialized faster algorithms are used.
Special values (NaN, Inf) are not handled.
| src | input array. |
| power | exponent of power. |
| dst | output array of the same size and type as src. |
| double cv::PSNR | ( | InputArray | src1, |
| InputArray | src2 | ||
| ) |
computes PSNR image/video quality metric
see http://en.wikipedia.org/wiki/Peak_signal-to-noise_ratio for details
| void cv::randn | ( | InputOutputArray | dst, |
| InputArray | mean, | ||
| InputArray | stddev | ||
| ) |
Fills the array with normally distributed random numbers.
The function randn fills the matrix dst with normally distributed random numbers with the specified mean vector and the standard deviation matrix. The generated random numbers are clipped to fit the value range of the output array data type.
| dst | output array of random numbers; the array must be pre-allocated and have 1 to 4 channels. |
| mean | mean value (expectation) of the generated random numbers. |
| stddev | standard deviation of the generated random numbers; it can be either a vector (in which case a diagonal standard deviation matrix is assumed) or a square matrix. |
| void cv::randShuffle | ( | InputOutputArray | dst, |
| double | iterFactor = 1., |
||
| RNG * | rng = 0 |
||
| ) |
Shuffles the array elements randomly.
The function randShuffle shuffles the specified 1D array by randomly choosing pairs of elements and swapping them. The number of such swap operations will be dst.rows*dst.cols*iterFactor .
| dst | input/output numerical 1D array. |
| iterFactor | scale factor that determines the number of random swap operations (see the details below). |
| rng | optional random number generator used for shuffling; if it is zero, theRNG () is used instead. |
| void cv::randu | ( | InputOutputArray | dst, |
| InputArray | low, | ||
| InputArray | high | ||
| ) |
Generates a single uniformly-distributed random number or an array of random numbers.
Non-template variant of the function fills the matrix dst with uniformly-distributed random numbers from the specified range:
\[\texttt{low} _c \leq \texttt{dst} (I)_c < \texttt{high} _c\]
| dst | output array of random numbers; the array must be pre-allocated. |
| low | inclusive lower boundary of the generated random numbers. |
| high | exclusive upper boundary of the generated random numbers. |
| void cv::reduce | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | dim, | ||
| int | rtype, | ||
| int | dtype = -1 |
||
| ) |
Reduces a matrix to a vector.
The function reduce reduces the matrix to a vector by treating the matrix rows/columns as a set of 1D vectors and performing the specified operation on the vectors until a single row/column is obtained. For example, the function can be used to compute horizontal and vertical projections of a raster image. In case of REDUCE_SUM and REDUCE_AVG , the output may have a larger element bit-depth to preserve accuracy. And multi-channel arrays are also supported in these two reduction modes.
| src | input 2D matrix. |
| dst | output vector. Its size and type is defined by dim and dtype parameters. |
| dim | dimension index along which the matrix is reduced. 0 means that the matrix is reduced to a single row. 1 means that the matrix is reduced to a single column. |
| rtype | reduction operation that could be one of cv::ReduceTypes |
| dtype | when negative, the output vector will have the same type as the input matrix, otherwise, its type will be CV_MAKE_TYPE(CV_MAT_DEPTH(dtype), src.channels()). |
| void cv::repeat | ( | InputArray | src, |
| int | ny, | ||
| int | nx, | ||
| OutputArray | dst | ||
| ) |
Fills the output array with repeated copies of the input array.
The functions repeat duplicate the input array one or more times along each of the two axes:
\[\texttt{dst} _{ij}= \texttt{src} _{i\mod src.rows, \; j\mod src.cols }\]
The second variant of the function is more convenient to use with MatrixExpressions.
| src | input array to replicate. |
| dst | output array of the same type as src. |
| ny | Flag to specify how many times the src is repeated along the vertical axis. |
| nx | Flag to specify how many times the src is repeated along the horizontal axis. |
| Mat cv::repeat | ( | const Mat & | src, |
| int | ny, | ||
| int | nx | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src | input array to replicate. |
| ny | Flag to specify how many times the src is repeated along the vertical axis. |
| nx | Flag to specify how many times the src is repeated along the horizontal axis. |
| void cv::scaleAdd | ( | InputArray | src1, |
| double | alpha, | ||
| InputArray | src2, | ||
| OutputArray | dst | ||
| ) |
Calculates the sum of a scaled array and another array.
The function scaleAdd is one of the classical primitive linear algebra operations, known as DAXPY or SAXPY in BLAS. It calculates the sum of a scaled array and another array:
\[\texttt{dst} (I)= \texttt{scale} \cdot \texttt{src1} (I) + \texttt{src2} (I)\]
The function can also be emulated with a matrix expression, for example:
| src1 | first input array. |
| alpha | scale factor for the first array. |
| src2 | second input array of the same size and type as src1. |
| dst | output array of the same size and type as src1. |
| void cv::setIdentity | ( | InputOutputArray | mtx, |
| const Scalar & | s = Scalar(1) |
||
| ) |
Initializes a scaled identity matrix.
The function setIdentity initializes a scaled identity matrix:
\[\texttt{mtx} (i,j)= \fork{\texttt{value}}{ if \(i=j\)}{0}{otherwise}\]
The function can also be emulated using the matrix initializers and the matrix expressions:
| mtx | matrix to initialize (not necessarily square). |
| s | value to assign to diagonal elements. |
| bool cv::solve | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| int | flags = DECOMP_LU |
||
| ) |
Solves one or more linear systems or least-squares problems.
The function solve solves a linear system or least-squares problem (the latter is possible with SVD or QR methods, or by specifying the flag DECOMP_NORMAL ):
\[\texttt{dst} = \arg \min _X \| \texttt{src1} \cdot \texttt{X} - \texttt{src2} \|\]
If DECOMP_LU or DECOMP_CHOLESKY method is used, the function returns 1 if src1 (or \(\texttt{src1}^T\texttt{src1}\) ) is non-singular. Otherwise, it returns 0. In the latter case, dst is not valid. Other methods find a pseudo-solution in case of a singular left-hand side part.
| src1 | input matrix on the left-hand side of the system. |
| src2 | input matrix on the right-hand side of the system. |
| dst | output solution. |
| flags | solution (matrix inversion) method (cv::DecompTypes) |
| int cv::solveCubic | ( | InputArray | coeffs, |
| OutputArray | roots | ||
| ) |
Finds the real roots of a cubic equation.
The function solveCubic finds the real roots of a cubic equation:
\[\texttt{coeffs} [0] x^3 + \texttt{coeffs} [1] x^2 + \texttt{coeffs} [2] x + \texttt{coeffs} [3] = 0\]
\[x^3 + \texttt{coeffs} [0] x^2 + \texttt{coeffs} [1] x + \texttt{coeffs} [2] = 0\]
The roots are stored in the roots array.
| coeffs | equation coefficients, an array of 3 or 4 elements. |
| roots | output array of real roots that has 1 or 3 elements. |
| double cv::solvePoly | ( | InputArray | coeffs, |
| OutputArray | roots, | ||
| int | maxIters = 300 |
||
| ) |
Finds the real or complex roots of a polynomial equation.
The function solvePoly finds real and complex roots of a polynomial equation:
\[\texttt{coeffs} [n] x^{n} + \texttt{coeffs} [n-1] x^{n-1} + ... + \texttt{coeffs} [1] x + \texttt{coeffs} [0] = 0\]
| coeffs | array of polynomial coefficients. |
| roots | output (complex) array of roots. |
| maxIters | maximum number of iterations the algorithm does. |
| void cv::sort | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flags | ||
| ) |
Sorts each row or each column of a matrix.
The function sort sorts each matrix row or each matrix column in ascending or descending order. So you should pass two operation flags to get desired behaviour. If you want to sort matrix rows or columns lexicographically, you can use STL std::sort generic function with the proper comparison predicate.
| src | input single-channel array. |
| dst | output array of the same size and type as src. |
| flags | operation flags, a combination of cv::SortFlags |
| void cv::sortIdx | ( | InputArray | src, |
| OutputArray | dst, | ||
| int | flags | ||
| ) |
Sorts each row or each column of a matrix.
The function sortIdx sorts each matrix row or each matrix column in the ascending or descending order. So you should pass two operation flags to get desired behaviour. Instead of reordering the elements themselves, it stores the indices of sorted elements in the output array. For example:
| src | input single-channel array. |
| dst | output integer array of the same size as src. |
| flags | operation flags that could be a combination of cv::SortFlags |
Divides a multi-channel array into several single-channel arrays.
The functions split split a multi-channel array into separate single-channel arrays:
\[\texttt{mv} [c](I) = \texttt{src} (I)_c\]
If you need to extract a single channel or do some other sophisticated channel permutation, use mixChannels .
| src | input multi-channel array. |
| mvbegin | output array; the number of arrays must match src.channels(); the arrays themselves are reallocated, if needed. |
| void cv::split | ( | InputArray | m, |
| OutputArrayOfArrays | mv | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| m | input multi-channel array. |
| mv | output vector of arrays; the arrays themselves are reallocated, if needed. |
| void cv::sqrt | ( | InputArray | src, |
| OutputArray | dst | ||
| ) |
Calculates a square root of array elements.
The functions sqrt calculate a square root of each input array element. In case of multi-channel arrays, each channel is processed independently. The accuracy is approximately the same as of the built-in std::sqrt .
| src | input floating-point array. |
| dst | output array of the same size and type as src. |
| void cv::subtract | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst, | ||
| InputArray | mask = noArray(), |
||
| int | dtype = -1 |
||
| ) |
Calculates the per-element difference between two arrays or array and a scalar.
The function subtract calculates:
\[\texttt{dst}(I) = \texttt{saturate} ( \texttt{src1}(I) - \texttt{src2}(I)) \quad \texttt{if mask}(I) \ne0\]
src1.channels(): \[\texttt{dst}(I) = \texttt{saturate} ( \texttt{src1}(I) - \texttt{src2} ) \quad \texttt{if mask}(I) \ne0\]
src2.channels(): \[\texttt{dst}(I) = \texttt{saturate} ( \texttt{src1} - \texttt{src2}(I) ) \quad \texttt{if mask}(I) \ne0\]
SubRS: \[\texttt{dst}(I) = \texttt{saturate} ( \texttt{src2} - \texttt{src1}(I) ) \quad \texttt{if mask}(I) \ne0\]
where I is a multi-dimensional index of array elements. In case of multi-channel arrays, each channel is processed independently.The first function in the list above can be replaced with matrix expressions:
The input arrays and the output array can all have the same or different depths. For example, you can subtract to 8-bit unsigned arrays and store the difference in a 16-bit signed array. Depth of the output array is determined by dtype parameter. In the second and third cases above, as well as in the first case, when src1.depth() == src2.depth(), dtype can be set to the default -1. In this case the output array will have the same depth as the input array, be it src1, src2 or both.
| src1 | first input array or a scalar. |
| src2 | second input array or a scalar. |
| dst | output array of the same size and the same number of channels as the input array. |
| mask | optional operation mask; this is an 8-bit single channel array that specifies elements of the output array to be changed. |
| dtype | optional depth of the output array |
| Scalar cv::sum | ( | InputArray | src | ) |
Calculates the sum of array elements.
The functions sum calculate and return the sum of array elements, independently for each channel.
| src | input array that must have from 1 to 4 channels. |
| void cv::SVBackSubst | ( | InputArray | w, |
| InputArray | u, | ||
| InputArray | vt, | ||
| InputArray | rhs, | ||
| OutputArray | dst | ||
| ) |
wrap SVD::backSubst
| void cv::SVDecomp | ( | InputArray | src, |
| OutputArray | w, | ||
| OutputArray | u, | ||
| OutputArray | vt, | ||
| int | flags = 0 |
||
| ) |
wrap SVD::compute
| RNG& cv::theRNG | ( | ) |
Returns the default random number generator.
The function theRNG returns the default random number generator. For each thread, there is a separate random number generator, so you can use the function safely in multi-thread environments. If you just need to get a single random number using this generator or initialize an array, you can use randu or randn instead. But if you are going to generate many random numbers inside a loop, it is much faster to use this function to retrieve the generator and then use RNG::operator _Tp() .
| Scalar cv::trace | ( | InputArray | mtx | ) |
Returns the trace of a matrix.
The function trace returns the sum of the diagonal elements of the matrix mtx .
\[\mathrm{tr} ( \texttt{mtx} ) = \sum _i \texttt{mtx} (i,i)\]
| mtx | input matrix. |
| void cv::transform | ( | InputArray | src, |
| OutputArray | dst, | ||
| InputArray | m | ||
| ) |
Performs the matrix transformation of every array element.
The function transform performs the matrix transformation of every element of the array src and stores the results in dst :
\[\texttt{dst} (I) = \texttt{m} \cdot \texttt{src} (I)\]
(when m.cols=src.channels() ), or
\[\texttt{dst} (I) = \texttt{m} \cdot [ \texttt{src} (I); 1]\]
(when m.cols=src.channels()+1 )
Every element of the N -channel array src is interpreted as N -element vector that is transformed using the M x N or M x (N+1) matrix m to M-element vector - the corresponding element of the output array dst .
The function may be used for geometrical transformation of N -dimensional points, arbitrary linear color space transformation (such as various kinds of RGB to YUV transforms), shuffling the image channels, and so forth.
| src | input array that must have as many channels (1 to 4) as m.cols or m.cols-1. |
| dst | output array of the same size and depth as src; it has as many channels as m.rows. |
| m | transformation 2x2 or 2x3 floating-point matrix. |
| void cv::transpose | ( | InputArray | src, |
| OutputArray | dst | ||
| ) |
Transposes a matrix.
The function transpose transposes the matrix src :
\[\texttt{dst} (i,j) = \texttt{src} (j,i)\]
| src | input array. |
| dst | output array of the same type as src. |
| void cv::vconcat | ( | const Mat * | src, |
| size_t | nsrc, | ||
| OutputArray | dst | ||
| ) |
Applies vertical concatenation to given matrices.
The function vertically concatenates two or more cv::Mat matrices (with the same number of cols).
| src | input array or vector of matrices. all of the matrices must have the same number of cols and the same depth. |
| nsrc | number of matrices in src. |
| dst | output array. It has the same number of cols and depth as the src, and the sum of rows of the src. |
| void cv::vconcat | ( | InputArray | src1, |
| InputArray | src2, | ||
| OutputArray | dst | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src1 | first input array to be considered for vertical concatenation. |
| src2 | second input array to be considered for vertical concatenation. |
| dst | output array. It has the same number of cols and depth as the src1 and src2, and the sum of rows of the src1 and src2. |
| void cv::vconcat | ( | InputArrayOfArrays | src, |
| OutputArray | dst | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
| src | input array or vector of matrices. all of the matrices must have the same number of cols and the same depth |
| dst | output array. It has the same number of cols and depth as the src, and the sum of rows of the src. same depth. |
 1.8.9.1
1.8.9.1