Proof of Theorem bnj1445
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | bnj1445.21 |
. 2
  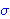                            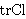           |
| 2 | | bnj1445.20 |
. . . . 5
     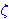            |
| 3 | | bnj1445.19 |
. . . . . . 7
  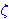       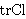          |
| 4 | | bnj1445.17 |
. . . . . . . . 9
            |
| 5 | | bnj1445.7 |
. . . . . . . . . . . . 13
              
      |
| 6 | | bnj1445.6 |
. . . . . . . . . . . . . . 15
      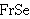
       |
| 7 | | nfv 1843 |
. . . . . . . . . . . . . . . 16
    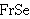
 |
| 8 | | bnj1445.5 |
. . . . . . . . . . . . . . . . . 18
             |
| 9 | | bnj1445.4 |
. . . . . . . . . . . . . . . . . . . . . 22
          
      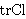           |
| 10 | | bnj1445.3 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
        
                       |
| 11 | | nfre1 3005 |
. . . . . . . . . . . . . . . . . . . . . . . . . 26
                            |
| 12 | 11 | nfab 2769 |
. . . . . . . . . . . . . . . . . . . . . . . . 25
        
                       |
| 13 | 10, 12 | nfcxfr 2762 |
. . . . . . . . . . . . . . . . . . . . . . . 24
    |
| 14 | 13 | nfcri 2758 |
. . . . . . . . . . . . . . . . . . . . . . 23
      |
| 15 | | nfv 1843 |
. . . . . . . . . . . . . . . . . . . . . . 23
           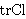         |
| 16 | 14, 15 | nfan 1828 |
. . . . . . . . . . . . . . . . . . . . . 22
                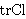          |
| 17 | 9, 16 | nfxfr 1779 |
. . . . . . . . . . . . . . . . . . . . 21
    |
| 18 | 17 | nfex 2154 |
. . . . . . . . . . . . . . . . . . . 20
      |
| 19 | 18 | nfn 1784 |
. . . . . . . . . . . . . . . . . . 19
       |
| 20 | | nfcv 2764 |
. . . . . . . . . . . . . . . . . . 19
    |
| 21 | 19, 20 | nfrab 3123 |
. . . . . . . . . . . . . . . . . 18
    
        |
| 22 | 8, 21 | nfcxfr 2762 |
. . . . . . . . . . . . . . . . 17
    |
| 23 | | nfcv 2764 |
. . . . . . . . . . . . . . . . 17
    |
| 24 | 22, 23 | nfne 2894 |
. . . . . . . . . . . . . . . 16
      |
| 25 | 7, 24 | nfan 1828 |
. . . . . . . . . . . . . . 15
     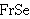   
   |
| 26 | 6, 25 | nfxfr 1779 |
. . . . . . . . . . . . . 14
    |
| 27 | 22 | nfcri 2758 |
. . . . . . . . . . . . . 14
      |
| 28 | | nfv 1843 |
. . . . . . . . . . . . . . 15
       |
| 29 | 22, 28 | nfral 2945 |
. . . . . . . . . . . . . 14
           |
| 30 | 26, 27, 29 | nf3an 1831 |
. . . . . . . . . . . . 13
        
    
     |
| 31 | 5, 30 | nfxfr 1779 |
. . . . . . . . . . . 12
    |
| 32 | 31 | nf5ri 2065 |
. . . . . . . . . . 11
        |
| 33 | 32 | bnj1351 30897 |
. . . . . . . . . 10
                    |
| 34 | 33 | nf5i 2024 |
. . . . . . . . 9
          |
| 35 | 4, 34 | nfxfr 1779 |
. . . . . . . 8
    |
| 36 | | nfv 1843 |
. . . . . . . 8
     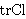        |
| 37 | 35, 36 | nfan 1828 |
. . . . . . 7
        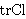         |
| 38 | 3, 37 | nfxfr 1779 |
. . . . . 6
   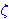 |
| 39 | | bnj1445.9 |
. . . . . . . 8
        
        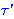  |
| 40 | | nfcv 2764 |
. . . . . . . . . 10
           |
| 41 | | bnj1445.8 |
. . . . . . . . . . 11
  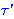      ![]. ].](_drbrack.gif)   |
| 42 | | nfcv 2764 |
. . . . . . . . . . . 12
    |
| 43 | 42, 17 | nfsbc 3457 |
. . . . . . . . . . 11
       ![]. ].](_drbrack.gif)  |
| 44 | 41, 43 | nfxfr 1779 |
. . . . . . . . . 10
   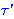 |
| 45 | 40, 44 | nfrex 3007 |
. . . . . . . . 9
              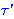 |
| 46 | 45 | nfab 2769 |
. . . . . . . 8
        
        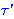  |
| 47 | 39, 46 | nfcxfr 2762 |
. . . . . . 7
    |
| 48 | 47 | nfcri 2758 |
. . . . . 6
      |
| 49 | | nfv 1843 |
. . . . . 6
       |
| 50 | 38, 48, 49 | nf3an 1831 |
. . . . 5
    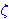    
      |
| 51 | 2, 50 | nfxfr 1779 |
. . . 4
    |
| 52 | 51 | nf5ri 2065 |
. . 3
        |
| 53 | | ax-5 1839 |
. . 3
                          |
| 54 | 14 | nf5ri 2065 |
. . 3
            |
| 55 | | ax-5 1839 |
. . 3
                                        |
| 56 | 52, 53, 54, 55 | bnj982 30849 |
. 2
                    |
| 57 | 1, 56 | hbxfrbi 1752 |
1
        |