Description: Rule of Generalization.
The postulated inference rule of predicate
calculus. See e.g. Rule 2 of [Hamilton] p. 74. This rule says that if
something is unconditionally true, then it is true for all values of a
variable. For example, if we have proved    , we can
conclude , we can
conclude
     or even or even
     . Theorem allt 32400
shows the
special case . Theorem allt 32400
shows the
special case   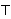 . Theorem spi 2054
shows we can go the other way
also: in other words we can add or remove universal quantifiers from the
beginning of any theorem as required. (Contributed by NM,
3-Jan-1993.) . Theorem spi 2054
shows we can go the other way
also: in other words we can add or remove universal quantifiers from the
beginning of any theorem as required. (Contributed by NM,
3-Jan-1993.) |