Description: Define a recursive
definition generator on  (the class of ordinal
numbers) with characteristic function (the class of ordinal
numbers) with characteristic function  and initial value and initial value  .
This combines functions .
This combines functions  in tfr1 7493 and in tfr1 7493 and  in tz7.44-1 7502 into one
definition. This rather amazing operation allows us to define, with
compact direct definitions, functions that are usually defined in
textbooks only with indirect self-referencing recursive definitions. A
recursive definition requires advanced metalogic to justify - in
particular, eliminating a recursive definition is very difficult and
often not even shown in textbooks. On the other hand, the elimination
of a direct definition is a matter of simple mechanical substitution.
The price paid is the daunting complexity of our in tz7.44-1 7502 into one
definition. This rather amazing operation allows us to define, with
compact direct definitions, functions that are usually defined in
textbooks only with indirect self-referencing recursive definitions. A
recursive definition requires advanced metalogic to justify - in
particular, eliminating a recursive definition is very difficult and
often not even shown in textbooks. On the other hand, the elimination
of a direct definition is a matter of simple mechanical substitution.
The price paid is the daunting complexity of our 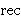 operation
(especially when df-recs 7468 that it is built on is also eliminated). But
once we get past this hurdle, definitions that would otherwise be
recursive become relatively simple, as in for example oav 7591,
from which
we prove the recursive textbook definition as theorems oa0 7596,
oasuc 7604,
and oalim 7612 (with the help of theorems rdg0 7517,
rdgsuc 7520, and
rdglim2a 7529). We can also restrict the operation
(especially when df-recs 7468 that it is built on is also eliminated). But
once we get past this hurdle, definitions that would otherwise be
recursive become relatively simple, as in for example oav 7591,
from which
we prove the recursive textbook definition as theorems oa0 7596,
oasuc 7604,
and oalim 7612 (with the help of theorems rdg0 7517,
rdgsuc 7520, and
rdglim2a 7529). We can also restrict the 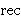 operation to define
otherwise recursive functions on the natural numbers operation to define
otherwise recursive functions on the natural numbers  ; see
fr0g 7531 and frsuc 7532. Our ; see
fr0g 7531 and frsuc 7532. Our 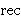 operation apparently does not appear
in published literature, although closely related is Definition 25.2 of
[Quine] p. 177, which he uses to
"turn...a recursion into a genuine or
direct definition" (p. 174). Note that the operation apparently does not appear
in published literature, although closely related is Definition 25.2 of
[Quine] p. 177, which he uses to
"turn...a recursion into a genuine or
direct definition" (p. 174). Note that the  operations (see
df-if 4087) select cases based on whether the domain of operations (see
df-if 4087) select cases based on whether the domain of
 is zero, a
successor, or a limit ordinal. is zero, a
successor, or a limit ordinal.
An important use of this definition is in the recursive sequence
generator df-seq 12802 on the natural numbers (as a subset of the
complex
numbers), allowing us to define, with direct definitions, recursive
infinite sequences such as the factorial function df-fac 13061 and integer
powers df-exp 12861.
Note: We introduce 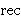 with the philosophical goal of being
able to eliminate all definitions with direct mechanical
substitution
and to verify easily the soundness of definitions. Metamath
itself
has no built-in technical limitation that prevents multiple-part
recursive definitions in the traditional textbook style.
(Contributed
by NM, 9-Apr-1995.) (Revised by Mario Carneiro,
9-May-2015.) with the philosophical goal of being
able to eliminate all definitions with direct mechanical
substitution
and to verify easily the soundness of definitions. Metamath
itself
has no built-in technical limitation that prevents multiple-part
recursive definitions in the traditional textbook style.
(Contributed
by NM, 9-Apr-1995.) (Revised by Mario Carneiro,
9-May-2015.) |