Proof of Theorem dp53lemd
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | lea 160 |
. . 3
 b0 b0   a0 a0  p0 p0  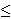 b0 b0 |
| 2 | | leor 159 |
. . . 4
 b0 b0   a0 a0  p0 p0  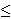  b1 b1   b0 b0   a0 a0  p0 p0   |
| 3 | | dp53lem.1 |
. . . . 5
c0 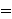   a1 a1  a2 a2   b1 b1  b2 b2  |
| 4 | | dp53lem.2 |
. . . . 5
c1 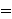   a0 a0  a2 a2   b0 b0  b2 b2  |
| 5 | | dp53lem.3 |
. . . . 5
c2 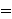   a0 a0  a1 a1   b0 b0  b1 b1  |
| 6 | | dp53lem.4 |
. . . . 5
p0 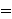   a1 a1  b1 b1   a2 a2  b2 b2  |
| 7 | | dp53lem.5 |
. . . . 5
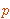 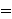    a0 a0  b0 b0   a1 a1  b1 b1    a2 a2
 b2 b2  |
| 8 | 3, 4, 5, 6, 7 | dp53lema 1161 |
. . . 4
 b1 b1   b0 b0   a0 a0  p0 p0   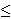  b1 b1    a0 a0  a1 a1 
 c0 c0  c1 c1   |
| 9 | 2, 8 | letr 137 |
. . 3
 b0 b0   a0 a0  p0 p0  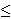  b1 b1    a0 a0  a1 a1   c0 c0  c1 c1   |
| 10 | 1, 9 | ler2an 173 |
. 2
 b0 b0   a0 a0  p0 p0  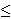  b0 b0   b1 b1    a0 a0  a1 a1 
 c0 c0  c1 c1    |
| 11 | 3, 4, 5, 6, 7 | dp53lemc 1163 |
. . . 4
 b0 b0     a0 a0
 b0 b0  b1
b1   c2 c2   c0 c0  c1 c1    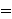  b0 b0   b1 b1   c2 c2   c0 c0
 c1 c1    |
| 12 | 3, 4, 5, 6, 7 | dp53lemb 1162 |
. . . 4
 b0 b0   b1 b1   c2 c2   c0 c0
 c1 c1    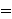  b0 b0   b1 b1    a0 a0  a1 a1 
 c0 c0  c1 c1    |
| 13 | 11, 12 | tr 62 |
. . 3
 b0 b0     a0 a0
 b0 b0  b1
b1   c2 c2   c0 c0  c1 c1    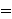  b0 b0   b1 b1    a0 a0  a1 a1 
 c0 c0  c1 c1    |
| 14 | 13 | cm 61 |
. 2
 b0 b0   b1 b1    a0 a0  a1 a1 
 c0 c0  c1 c1    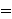  b0 b0
    a0 a0  b0 b0  b1 b1 
 c2 c2   c0 c0  c1 c1    |
| 15 | 10, 14 | lbtr 139 |
1
 b0 b0   a0 a0  p0 p0  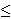  b0 b0     a0 a0
 b0 b0  b1
b1   c2 c2   c0 c0  c1 c1    |