Graph optimization¶
In this section we will define a couple optimizations on doubles.
Todo
This tutorial goes way too far under the hood, for someone who just wants to add yet another pattern to the libraries in tensor.opt for example.
We need another tutorial that covers the decorator syntax, and explains how to register your optimization right away. That’s what you need to get going.
Later, the rest is more useful for when that decorator syntax type thing doesn’t work. (There are optimizations that don’t fit that model).
Note
The optimization tag cxx_only is used for optimizations that insert Ops which have no Python implementation (so they only have C code). Optimizations with this tag are skipped when there is no C++ compiler available.
Global and local optimizations¶
First, let’s lay out the way optimizations work in Theano. There are
two types of optimizations: global optimizations and local
optimizations. A global optimization takes a FunctionGraph object (a
FunctionGraph is a wrapper around a whole computation graph, you can see its
documentation for more details) and navigates through it
in a suitable way, replacing some Variables by others in the process. A
local optimization, on the other hand, is defined as a function on a
single Apply node and must return either False (to mean that
nothing is to be done) or a list of new Variables that we would like to
replace the node’s outputs with. A Navigator is a special kind
of global optimization which navigates the computation graph in some
fashion (in topological order, reverse-topological order, random
order, etc.) and applies one or more local optimizations at each step.
Optimizations which are holistic, meaning that they must take into account dependencies that might be all over the graph, should be global. Optimizations that can be done with a narrow perspective are better defined as local optimizations. The majority of optimizations we want to define are local.
Global optimization¶
A global optimization (or optimizer) is an object which defines the following methods:
-
class
Optimizer¶ -
apply(fgraph)¶ This method takes a FunctionGraph object which contains the computation graph and does modifications in line with what the optimization is meant to do. This is one of the main methods of the optimizer.
-
add_requirements(fgraph)¶ This method takes a FunctionGraph object and adds features to it. These features are “plugins” that are needed for the
applymethod to do its job properly.
-
optimize(fgraph)¶ This is the interface function called by Theano.
Default: this is defined by Optimizer as
add_requirement(fgraph); apply(fgraph).
-
See the section about FunctionGraph to understand how to define these
methods.
Local optimization¶
A local optimization is an object which defines the following methods:
-
class
LocalOptimizer¶ -
transform(node)¶ This method takes an Apply node and returns either
Falseto signify that no changes are to be done or a list of Variables which matches the length of the node’soutputslist. When the LocalOptimizer is applied by a Navigator, the outputs of the node passed as argument to the LocalOptimizer will be replaced by the list returned.
-
One simplification rule¶
For starters, let’s define the following simplification:
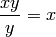
We will implement it in three ways: using a global optimization, a local optimization with a Navigator and then using the PatternSub facility.
Global optimization¶
Here is the code for a global optimization implementing the simplification described above:
import theano
from theano import gof
from theano.gof import toolbox
class Simplify(gof.Optimizer):
def add_requirements(self, fgraph):
fgraph.attach_feature(toolbox.ReplaceValidate())
def apply(self, fgraph):
for node in fgraph.toposort():
if node.op == true_div:
x, y = node.inputs
z = node.outputs[0]
if x.owner and x.owner.op == mul:
a, b = x.owner.inputs
if y == a:
fgraph.replace_validate(z, b)
elif y == b:
fgraph.replace_validate(z, a)
simplify = Simplify()
Todo
What is add_requirements? Why would we know to do this? Are there other requirements we might want to know about?
Here’s how it works: first, in add_requirements, we add the
ReplaceValidate FunctionGraph Features located in
toolbox – [doc TODO]. This feature adds the replace_validate
method to fgraph, which is an enhanced version of replace that
does additional checks to ensure that we are not messing up the
computation graph (note: if ReplaceValidate was already added by
another optimizer, extend will do nothing). In a nutshell,
toolbox.ReplaceValidate grants access to fgraph.replace_validate,
and fgraph.replace_validate allows us to replace a Variable with
another while respecting certain validation constraints. You can
browse the list of FunctionGraph Feature List and see if some of
them might be useful to write optimizations with. For example, as an
exercise, try to rewrite Simplify using NodeFinder. (Hint: you
want to use the method it publishes instead of the call to toposort!)
Then, in apply we do the actual job of simplification. We start by
iterating through the graph in topological order. For each node
encountered, we check if it’s a div node. If not, we have nothing
to do here. If so, we put in x, y and z the numerator,
denominator and quotient (output) of the division.
The simplification only occurs when the numerator is a multiplication,
so we check for that. If the numerator is a multiplication we put the
two operands in a and b, so
we can now say that z == (a*b)/y. If y==a then z==b and if
y==b then z==a. When either case happens then we can replace
z by either a or b using fgraph.replace_validate - else we do
nothing. You might want to check the documentation about Variable
and Apply to get a better understanding of the
pointer-following game you need to get ahold of the nodes of interest
for the simplification (x, y, z, a, b, etc.).
Test time:
>>> from theano.scalar import float64, add, mul, true_div
>>> x = float64('x')
>>> y = float64('y')
>>> z = float64('z')
>>> a = add(z, mul(true_div(mul(y, x), y), true_div(z, x)))
>>> e = gof.FunctionGraph([x, y, z], [a])
>>> e
[add(z, mul(true_div(mul(y, x), y), true_div(z, x)))]
>>> simplify.optimize(e)
>>> e
[add(z, mul(x, true_div(z, x)))]
Cool! It seems to work. You can check what happens if you put many
instances of 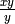 in the graph. Note that it sometimes
won’t work for reasons that have nothing to do with the quality of the
optimization you wrote. For example, consider the following:
in the graph. Note that it sometimes
won’t work for reasons that have nothing to do with the quality of the
optimization you wrote. For example, consider the following:
>>> x = float64('x')
>>> y = float64('y')
>>> z = float64('z')
>>> a = true_div(mul(add(y, z), x), add(y, z))
>>> e = gof.FunctionGraph([x, y, z], [a])
>>> e
[true_div(mul(add(y, z), x), add(y, z))]
>>> simplify.optimize(e)
>>> e
[true_div(mul(add(y, z), x), add(y, z))]
Nothing happened here. The reason is: add(y, z) != add(y,
z). That is the case for efficiency reasons. To fix this problem we
first need to merge the parts of the graph that represent the same
computation, using the merge_optimizer defined in
theano.gof.opt.
>>> from theano.gof.opt import merge_optimizer
>>> merge_optimizer.optimize(e)
(0, ..., None, None, {}, 1, 0)
>>> e
[true_div(mul(*1 -> add(y, z), x), *1)]
>>> simplify.optimize(e)
>>> e
[x]
Once the merge is done, both occurrences of add(y, z) are
collapsed into a single one and is used as an input in two
places. Note that add(x, y) and add(y, x) are still considered
to be different because Theano has no clue that add is
commutative. You may write your own global optimizer to identify
computations that are identical with full knowledge of the rules of
arithmetics that your Ops implement. Theano might provide facilities
for this somewhere in the future.
Note
FunctionGraph is a Theano structure intended for the optimization
phase. It is used internally by function and is rarely
exposed to the end user. You can use it to test out optimizations,
etc. if you are comfortable with it, but it is recommended to use
the function frontend and to interface optimizations with
optdb (we’ll see how to do that soon).
Local optimization¶
The local version of the above code would be the following:
class LocalSimplify(gof.LocalOptimizer):
def transform(self, node):
if node.op == true_div:
x, y = node.inputs
if x.owner and x.owner.op == mul:
a, b = x.owner.inputs
if y == a:
return [b]
elif y == b:
return [a]
return False
def tracks(self):
# This should be needed for the EquilibriumOptimizer
# but it isn't now
# TODO: do this and explain it
return [] # that's not what you should do
local_simplify = LocalSimplify()
Todo
Fix up previous example... it’s bad and incomplete.
The definition of transform is the inner loop of the global optimizer,
where the node is given as argument. If no changes are to be made,
False must be returned. Else, a list of what to replace the node’s
outputs with must be returned. This list must have the same length as
node.ouputs. If one of node.outputs don’t have clients(it is not used
in the graph), you can put None in the returned list to remove it.
In order to apply the local optimizer we must use it in conjunction with a Navigator. Basically, a Navigator is a global optimizer that loops through all nodes in the graph (or a well-defined subset of them) and applies one or several local optimizers on them.
>>> x = float64('x')
>>> y = float64('y')
>>> z = float64('z')
>>> a = add(z, mul(true_div(mul(y, x), y), true_div(z, x)))
>>> e = gof.FunctionGraph([x, y, z], [a])
>>> e
[add(z, mul(true_div(mul(y, x), y), true_div(z, x)))]
>>> simplify = gof.TopoOptimizer(local_simplify)
>>> simplify.optimize(e)
(<theano.gof.opt.TopoOptimizer object at 0x...>, 1, 5, 3, ..., ..., ...)
>>> e
[add(z, mul(x, true_div(z, x)))]
OpSub, OpRemove, PatternSub¶
Theano defines some shortcuts to make LocalOptimizers:
-
OpSub(op1, op2)¶ Replaces all uses of op1 by op2. In other words, the outputs of all Apply involving op1 by the outputs of Apply nodes involving op2, where their inputs are the same.
-
OpRemove(op)¶ Removes all uses of op in the following way: if
y = op(x)thenyis replaced byx. op must have as many outputs as it has inputs. The first output becomes the first input, the second output becomes the second input, and so on.
-
PatternSub(pattern1, pattern2)¶ Replaces all occurrences of the first pattern by the second pattern. See
PatternSub.
from theano.gof.opt import OpSub, OpRemove, PatternSub
# Replacing add by mul (this is not recommended for primarily
# mathematical reasons):
add_to_mul = OpSub(add, mul)
# Removing identity
remove_identity = OpRemove(identity)
# The "simplify" operation we've been defining in the past few
# sections. Note that we need two patterns to account for the
# permutations of the arguments to mul.
local_simplify_1 = PatternSub((true_div, (mul, 'x', 'y'), 'y'),
'x')
local_simplify_2 = PatternSub((true_div, (mul, 'x', 'y'), 'x'),
'y')
Note
OpSub, OpRemove and PatternSub produce local optimizers, which
means that everything we said previously about local optimizers
apply: they need to be wrapped in a Navigator, etc.
Todo
wtf is a navigator?
When an optimization can be naturally expressed using OpSub, OpRemove
or PatternSub, it is highly recommended to use them.
WRITEME: more about using PatternSub (syntax for the patterns, how to
use constraints, etc. - there’s some decent doc at
PatternSub for those interested)
The optimization database (optdb)¶
Theano exports a symbol called optdb which acts as a sort of
ordered database of optimizations. When you make a new optimization,
you must insert it at the proper place in the database. Furthermore,
you can give each optimization in the database a set of tags that can
serve as a basis for filtering.
The point of optdb is that you might want to apply many optimizations to a computation graph in many unique patterns. For example, you might want to do optimization X, then optimization Y, then optimization Z. And then maybe optimization Y is an EquilibriumOptimizer containing LocalOptimizers A, B and C which are applied on every node of the graph until they all fail to change it. If some optimizations act up, we want an easy way to turn them off. Ditto if some optimizations are very CPU-intensive and we don’t want to take the time to apply them.
The optdb system allows us to tag each optimization with a unique name as well as informative tags such as ‘stable’, ‘buggy’ or ‘cpu_intensive’, all this without compromising the structure of the optimizations.
Definition of optdb¶
optdb is an object which is an instance of
SequenceDB,
itself a subclass of DB.
There exist (for now) two types of DB, SequenceDB and EquilibriumDB.
When given an appropriate Query, DB objects build an Optimizer matching
the query.
A SequenceDB contains Optimizer or DB objects. Each of them has a name, an arbitrary number of tags and an integer representing their order in the sequence. When a Query is applied to a SequenceDB, all Optimizers whose tags match the query are inserted in proper order in a SequenceOptimizer, which is returned. If the SequenceDB contains DB instances, the Query will be passed to them as well and the optimizers they return will be put in their places.
An EquilibriumDB contains LocalOptimizer or DB objects. Each of them has a name and an arbitrary number of tags. When a Query is applied to an EquilibriumDB, all LocalOptimizers that match the query are inserted into an EquilibriumOptimizer, which is returned. If the SequenceDB contains DB instances, the Query will be passed to them as well and the LocalOptimizers they return will be put in their places (note that as of yet no DB can produce LocalOptimizer objects, so this is a moot point).
Theano contains one principal DB object, optdb, which
contains all of Theano’s optimizers with proper tags. It is
recommended to insert new Optimizers in it. As mentioned previously,
optdb is a SequenceDB, so, at the top level, Theano applies a sequence
of global optimizations to the computation graphs.
Query¶
A Query is built by the following call:
theano.gof.Query(include, require=None, exclude=None, subquery=None)
-
class
Query¶ -
include¶ A set of tags (a tag being a string) such that every optimization obtained through this Query must have one of the tags listed. This field is required and basically acts as a starting point for the search.
-
require¶ A set of tags such that every optimization obtained through this Query must have all of these tags.
-
exclude¶ A set of tags such that every optimization obtained through this Query must have none of these tags.
-
subquery¶ optdb can contain sub-databases; subquery is a dictionary mapping the name of a sub-database to a special Query. If no subquery is given for a sub-database, the original Query will be used again.
-
Furthermore, a Query object includes three methods, including,
requiring and excluding which each produce a new Query object
with include, require and exclude sets refined to contain the new [WRITEME]
Examples¶
Here are a few examples of how to use a Query on optdb to produce an Optimizer:
from theano.gof import Query
from theano.compile import optdb
# This is how the optimizer for the fast_run mode is defined
fast_run = optdb.query(Query(include=['fast_run']))
# This is how the optimizer for the fast_compile mode is defined
fast_compile = optdb.query(Query(include=['fast_compile']))
# This is the same as fast_run but no optimizations will replace
# any operation by an inplace version. This assumes, of course,
# that all inplace operations are tagged as 'inplace' (as they
# should!)
fast_run_no_inplace = optdb.query(Query(include=['fast_run'],
exclude=['inplace']))
Registering an Optimizer¶
Let’s say we have a global optimizer called simplify. We can add
it to optdb as follows:
# optdb.register(name, optimizer, order, *tags)
optdb.register('simplify', simplify, 0.5, 'fast_run')
Once this is done, the FAST_RUN mode will automatically include your optimization (since you gave it the ‘fast_run’ tag). Of course, already-compiled functions will see no change. The ‘order’ parameter (what it means and how to choose it) will be explained in optdb structure below.
Registering a LocalOptimizer¶
LocalOptimizers may be registered in two ways:
- Wrap them in a Navigator and insert them like a global optimizer (see previous section).
- Put them in an EquilibriumDB.
Theano defines two EquilibriumDBs where you can put local optimizations:
-
canonicalize()¶ This contains optimizations that aim to simplify the graph:
- Replace rare or esoterical operations with their equivalents using elementary operations.
- Order operations in a canonical way (any sequence of
multiplications and divisions can be rewritten to contain at most
one division, for example;
x*xcan be rewrittenx**2; etc.) - Fold constants (
Constant(2)*Constant(2)becomesConstant(4))
-
specialize()¶ This contains optimizations that aim to specialize the graph:
- Replace a combination of operations with a special operation that does the same thing (but better).
For each group, all optimizations of the group that are selected by
the Query will be applied on the graph over and over again until none
of them is applicable, so keep that in mind when designing it: check
carefully that your optimization leads to a fixpoint (a point where it
cannot apply anymore) at which point it returns False to indicate its
job is done. Also be careful not to undo the work of another local
optimizer in the group, because then the graph will oscillate between
two or more states and nothing will get done.
optdb structure¶
optdb contains the following Optimizers and sub-DBs, with the given priorities and tags:
| Order | Name | Description |
|---|---|---|
| 0 | merge1 | First merge operation |
| 1 | canonicalize | Simplify the graph |
| 2 | specialize | Add specialized operations |
| 49 | merge2 | Second merge operation |
| 49.5 | add_destroy_handler | Enable inplace optimizations |
| 100 | merge3 | Third merge operation |
The merge operations are meant to put together parts of the graph that represent the same computation. Since optimizations can modify the graph in such a way that two previously different-looking parts of the graph become similar, we merge at the beginning, in the middle and at the very end. Technically, we only really need to do it at the end, but doing it in previous steps reduces the size of the graph and therefore increases the efficiency of the process.
See previous section for more information about the canonicalize and specialize steps.
The add_destroy_handler step is not really an optimization. It is
a marker. Basically:
Warning
Any optimization which inserts inplace operations in the
computation graph must appear after the add_destroy_handler
“optimizer”. In other words, the priority of any such optimization
must be >= 50. Failure to comply by this restriction can lead
to the creation of incorrect computation graphs.
The reason the destroy handler is not inserted at the beginning is that it is costly to run. It is cheaper to run most optimizations under the assumption there are no inplace operations.
Profiling Theano function compilation¶
You find that compiling a Theano function is taking too much time? You can get profiling information about Theano optimization. The normal Theano profiler will provide you with very high-level information. The indentation shows the included in/subset relationship between sections. The top of its output look like this:
Function profiling
==================
Message: PATH_TO_A_FILE:23
Time in 0 calls to Function.__call__: 0.000000e+00s
Total compile time: 1.131874e+01s
Number of Apply nodes: 50
Theano Optimizer time: 1.152431e+00s
Theano validate time: 2.790451e-02s
Theano Linker time (includes C, CUDA code generation/compiling): 7.893991e-02s
Import time 1.153541e-02s
Time in all call to theano.grad() 4.732513e-02s
Explanations:
Total compile time: 1.131874e+01sgives the total time spent inside theano.function.Number of Apply nodes: 50means that after optimization, there are 50 apply node in the graph.Theano Optimizer time: 1.152431e+00smeans that we spend 1.15s in thetheano.functionphase where we optimize (modify) the graph to make it faster / more stable numerically / work on GPU /...Theano validate time: 2.790451e-02smeans that we spent 2.8e-2s in the validate subset of the optimization phase.Theano Linker time (includes C, CUDA code generation/compiling): 7.893991e-02smeans that we spent 7.9e-2s in linker phase oftheano.function.Import time 1.153541e-02sis a subset of the linker time where we import the compiled module.Time in all call to theano.grad() 4.732513e-02stells that we spent a total of 4.7e-2s in all calls totheano.grad. This is outside of the calls totheano.function.
The linker phase includes the generation of the C code, the time spent by g++ to compile and the time needed by Theano to build the object we return. The C code generation and compilation is cached, so the first time you compile a function and the following ones could take different amount of execution time.
Detailed profiling of Theano optimizer¶
You can get more detailed profiling information about the Theano
optimizer phase by setting to True the Theano flags
config.profile_optimizer.
This will output something like this:
Optimizer Profile
-----------------
SeqOptimizer OPT_FAST_RUN time 1.152s for 123/50 nodes before/after optimization
0.028s for fgraph.validate()
0.131s for callback
time - (name, class, index) - validate time
0.751816s - ('canonicalize', 'EquilibriumOptimizer', 4) - 0.004s
EquilibriumOptimizer canonicalize
time 0.751s for 14 passes
nb nodes (start, end, max) 108 81 117
time io_toposort 0.029s
time in local optimizers 0.687s
time in global optimizers 0.010s
0 - 0.050s 27 (0.000s in global opts, 0.002s io_toposort) - 108 nodes - ('local_dimshuffle_lift', 9) ('local_upcast_elemwise_constant_inputs', 5) ('local_shape_to_shape_i', 3) ('local_fill_sink', 3) ('local_fill_to_alloc', 2) ...
1 - 0.288s 26 (0.002s in global opts, 0.002s io_toposort) - 117 nodes - ('local_dimshuffle_lift', 8) ('local_fill_sink', 4) ('constant_folding', 4) ('local_useless_elemwise', 3) ('local_subtensor_make_vector', 3) ...
2 - 0.044s 13 (0.002s in global opts, 0.003s io_toposort) - 96 nodes - ('constant_folding', 4) ('local_dimshuffle_lift', 3) ('local_fill_sink', 3) ('local_useless_elemwise', 1) ('local_fill_to_alloc', 1) ...
3 - 0.045s 11 (0.000s in global opts, 0.002s io_toposort) - 91 nodes - ('constant_folding', 3) ('local_fill_to_alloc', 2) ('local_dimshuffle_lift', 2) ('local_mul_canonizer', 2) ('MergeOptimizer', 1) ...
4 - 0.035s 8 (0.002s in global opts, 0.002s io_toposort) - 93 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1)
5 - 0.035s 6 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_fill_sink', 2) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('local_mul_canonizer', 1)
6 - 0.038s 10 (0.001s in global opts, 0.002s io_toposort) - 95 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 3) ('constant_folding', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1)
7 - 0.032s 5 (0.001s in global opts, 0.002s io_toposort) - 91 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1)
8 - 0.034s 5 (0.000s in global opts, 0.002s io_toposort) - 92 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_greedy_distributor', 1)
9 - 0.031s 6 (0.001s in global opts, 0.002s io_toposort) - 90 nodes - ('local_fill_sink', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1) ('local_greedy_distributor', 1)
10 - 0.032s 5 (0.000s in global opts, 0.002s io_toposort) - 89 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_fill_sink', 1)
11 - 0.030s 5 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1)
12 - 0.026s 1 (0.000s in global opts, 0.003s io_toposort) - 81 nodes - ('MergeOptimizer', 1)
13 - 0.031s 0 (0.000s in global opts, 0.003s io_toposort) - 81 nodes -
times - times applied - nb node created - name:
0.263s - 15 - 0 - constant_folding
0.096s - 2 - 14 - local_greedy_distributor
0.066s - 4 - 19 - local_mul_canonizer
0.046s - 28 - 57 - local_fill_sink
0.042s - 35 - 78 - local_dimshuffle_lift
0.018s - 5 - 15 - local_upcast_elemwise_constant_inputs
0.010s - 11 - 4 - MergeOptimizer
0.009s - 4 - 0 - local_useless_elemwise
0.005s - 11 - 2 - local_fill_to_alloc
0.004s - 3 - 6 - local_neg_to_mul
0.002s - 1 - 3 - local_lift_transpose_through_dot
0.002s - 3 - 4 - local_shape_to_shape_i
0.002s - 2 - 4 - local_subtensor_lift
0.001s - 3 - 0 - local_subtensor_make_vector
0.001s - 1 - 1 - local_sum_all_to_none
0.131s - in 62 optimization that where not used (display only those with a runtime > 0)
0.050s - local_add_canonizer
0.018s - local_mul_zero
0.016s - local_one_minus_erf
0.010s - local_func_inv
0.006s - local_0_dot_x
0.005s - local_track_shape_i
0.004s - local_mul_switch_sink
0.004s - local_fill_cut
0.004s - local_one_minus_erf2
0.003s - local_remove_switch_const_cond
0.003s - local_cast_cast
0.002s - local_IncSubtensor_serialize
0.001s - local_sum_div_dimshuffle
0.001s - local_div_switch_sink
0.001s - local_dimshuffle_no_inplace_at_canonicalize
0.001s - local_cut_useless_reduce
0.001s - local_reduce_join
0.000s - local_sum_sum
0.000s - local_useless_alloc
0.000s - local_reshape_chain
0.000s - local_useless_subtensor
0.000s - local_reshape_lift
0.000s - local_flatten_lift
0.000s - local_useless_slice
0.000s - local_subtensor_of_alloc
0.000s - local_subtensor_of_dot
0.000s - local_subtensor_merge
0.101733s - ('elemwise_fusion', 'SeqOptimizer', 13) - 0.000s
SeqOptimizer elemwise_fusion time 0.102s for 78/50 nodes before/after optimization
0.000s for fgraph.validate()
0.004s for callback
0.095307s - ('composite_elemwise_fusion', 'FusionOptimizer', 1) - 0.000s
FusionOptimizer
nb_iter 3
nb_replacement 10
nb_inconsistency_replace 0
validate_time 0.000249624252319
callback_time 0.00316381454468
time_toposort 0.00375390052795
0.006412s - ('local_add_mul_fusion', 'FusionOptimizer', 0) - 0.000s
FusionOptimizer
nb_iter 2
nb_replacement 3
nb_inconsistency_replace 0
validate_time 6.43730163574e-05
callback_time 0.000783205032349
time_toposort 0.0035240650177
0.090089s - ('inplace_elemwise_optimizer', 'FromFunctionOptimizer', 30) - 0.019s
0.048993s - ('BlasOpt', 'SeqOptimizer', 8) - 0.000s
SeqOptimizer BlasOpt time 0.049s for 81/80 nodes before/after optimization
0.000s for fgraph.validate()
0.003s for callback
0.035997s - ('gemm_optimizer', 'GemmOptimizer', 1) - 0.000s
GemmOptimizer
nb_iter 2
nb_replacement 2
nb_replacement_didn_t_remove 0
nb_inconsistency_make 0
nb_inconsistency_replace 0
time_canonicalize 0.00720071792603
time_factor_can 9.05990600586e-06
time_factor_list 0.00128507614136
time_toposort 0.00311398506165
validate_time 4.60147857666e-05
callback_time 0.00174236297607
0.004569s - ('local_dot_to_dot22', 'TopoOptimizer', 0) - 0.000s
TopoOptimizer
nb_node (start, end, changed) (81, 81, 5)
init io_toposort 0.00139284133911
loop time 0.00312399864197
callback_time 0.00172805786133
0.002283s - ('local_dot22_to_dot22scalar', 'TopoOptimizer', 2) - 0.000s
TopoOptimizer
nb_node (start, end, changed) (80, 80, 0)
init io_toposort 0.00171804428101
loop time 0.000502109527588
callback_time 0.0
0.002257s - ('local_gemm_to_gemv', 'EquilibriumOptimizer', 3) - 0.000s
EquilibriumOptimizer local_gemm_to_gemv
time 0.002s for 1 passes
nb nodes (start, end, max) 80 80 80
time io_toposort 0.001s
time in local optimizers 0.000s
time in global optimizers 0.000s
0 - 0.002s 0 (0.000s in global opts, 0.001s io_toposort) - 80 nodes -
0.002227s - ('use_c_blas', 'TopoOptimizer', 4) - 0.000s
TopoOptimizer
nb_node (start, end, changed) (80, 80, 0)
init io_toposort 0.0014750957489
loop time 0.00068998336792
callback_time 0.0
0.001632s - ('use_scipy_ger', 'TopoOptimizer', 5) - 0.000s
TopoOptimizer
nb_node (start, end, changed) (80, 80, 0)
init io_toposort 0.00138401985168
loop time 0.000202178955078
callback_time 0.0
0.031740s - ('specialize', 'EquilibriumOptimizer', 9) - 0.000s
EquilibriumOptimizer specialize
time 0.031s for 2 passes
nb nodes (start, end, max) 80 78 80
time io_toposort 0.003s
time in local optimizers 0.022s
time in global optimizers 0.004s
0 - 0.017s 6 (0.002s in global opts, 0.001s io_toposort) - 80 nodes - ('constant_folding', 2) ('local_mul_to_sqr', 1) ('local_elemwise_alloc', 1) ('local_div_to_inv', 1) ('local_mul_specialize', 1)
1 - 0.014s 0 (0.002s in global opts, 0.001s io_toposort) - 78 nodes -
times - times applied - nb node created - name:
0.003s - 1 - 1 - local_mul_specialize
0.002s - 1 - 2 - local_elemwise_alloc
0.002s - 2 - 0 - constant_folding
0.001s - 1 - 1 - local_div_to_inv
0.001s - 1 - 1 - local_mul_to_sqr
0.016s - in 69 optimization that where not used (display only those with a runtime > 0)
0.004s - crossentropy_to_crossentropy_with_softmax_with_bias
0.002s - local_one_minus_erf
0.002s - Elemwise{sub,no_inplace}(z, Elemwise{mul,no_inplace}(alpha subject to <function <lambda> at 0x7f475e4da050>, SparseDot(x, y))) -> Usmm{no_inplace}(Elemwise{neg,no_inplace}(alpha), x, y, z)
0.002s - local_add_specialize
0.001s - local_func_inv
0.001s - local_useless_elemwise
0.001s - local_abs_merge
0.001s - local_track_shape_i
0.000s - local_one_minus_erf2
0.000s - local_sum_mul_by_scalar
0.000s - local_elemwise_sub_zeros
0.000s - local_cast_cast
0.000s - local_alloc_unary
0.000s - Elemwise{log,no_inplace}(Softmax(x)) -> <function make_out_pattern at 0x7f47619a8410>(x)
0.000s - local_sum_div_dimshuffle
0.000s - local_sum_alloc
0.000s - local_dimshuffle_lift
0.000s - local_reduce_broadcastable
0.000s - local_grad_log_erfc_neg
0.000s - local_advanced_indexing_crossentropy_onehot
0.000s - local_log_erfc
0.000s - local_log1p
0.000s - local_log_add
0.000s - local_useless_alloc
0.000s - local_neg_neg
0.000s - local_neg_div_neg
...
To understand this profile here is some explanation of how optimizations work:
Optimizations are organized in an hierarchy. At the top level, there is a
SeqOptimizer(Sequence Optimizer). It contains other optimizers, and applies them in the order they were specified. Those sub-optimizers can be of other types, but are all global optimizers.Each Optimizer in the hierarchy will print some stats about itself. The information that it prints depends of the type of the optimizer.
The SeqOptimizer will print some stats at the start:
Optimizer Profile ----------------- SeqOptimizer OPT_FAST_RUN time 1.152s for 123/50 nodes before/after optimization 0.028s for fgraph.validate() 0.131s for callback time - (name, class, index) - validate time Then it will print, with some additional indentation, each sub-optimizer's profile information. These sub-profiles are ordered by the time they took to execute, not by their execution order.OPT_FAST_RUNis the name of the optimizer- 1.152s is the total time spent in that optimizer
- 123/50 means that before this optimization, there were 123 apply node in the function graph, and after only 50.
- 0.028s means it spent that time calls to
fgraph.validate() - 0.131s means it spent that time for callbacks. This is a mechanism that can trigger other execution when there is a change to the FunctionGraph.
time - (name, class, index) - validate timetells how the information for each sub-optimizer get printed.- All other instances of
SeqOptimizerare described like this. In particular, some sub-optimizer from OPT_FAST_RUN that are alsoSeqOptimizer.
The
SeqOptimizerwill print some stats at the start:0.751816s - ('canonicalize', 'EquilibriumOptimizer', 4) - 0.004s EquilibriumOptimizer canonicalize time 0.751s for 14 passes nb nodes (start, end, max) 108 81 117 time io_toposort 0.029s time in local optimizers 0.687s time in global optimizers 0.010s 0 - 0.050s 27 (0.000s in global opts, 0.002s io_toposort) - 108 nodes - ('local_dimshuffle_lift', 9) ('local_upcast_elemwise_constant_inputs', 5) ('local_shape_to_shape_i', 3) ('local_fill_sink', 3) ('local_fill_to_alloc', 2) ... 1 - 0.288s 26 (0.002s in global opts, 0.002s io_toposort) - 117 nodes - ('local_dimshuffle_lift', 8) ('local_fill_sink', 4) ('constant_folding', 4) ('local_useless_elemwise', 3) ('local_subtensor_make_vector', 3) ... 2 - 0.044s 13 (0.002s in global opts, 0.003s io_toposort) - 96 nodes - ('constant_folding', 4) ('local_dimshuffle_lift', 3) ('local_fill_sink', 3) ('local_useless_elemwise', 1) ('local_fill_to_alloc', 1) ... 3 - 0.045s 11 (0.000s in global opts, 0.002s io_toposort) - 91 nodes - ('constant_folding', 3) ('local_fill_to_alloc', 2) ('local_dimshuffle_lift', 2) ('local_mul_canonizer', 2) ('MergeOptimizer', 1) ... 4 - 0.035s 8 (0.002s in global opts, 0.002s io_toposort) - 93 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1) 5 - 0.035s 6 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_fill_sink', 2) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('local_mul_canonizer', 1) 6 - 0.038s 10 (0.001s in global opts, 0.002s io_toposort) - 95 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 3) ('constant_folding', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) 7 - 0.032s 5 (0.001s in global opts, 0.002s io_toposort) - 91 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1) 8 - 0.034s 5 (0.000s in global opts, 0.002s io_toposort) - 92 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_greedy_distributor', 1) 9 - 0.031s 6 (0.001s in global opts, 0.002s io_toposort) - 90 nodes - ('local_fill_sink', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1) ('local_greedy_distributor', 1) 10 - 0.032s 5 (0.000s in global opts, 0.002s io_toposort) - 89 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_fill_sink', 1) 11 - 0.030s 5 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1) 12 - 0.026s 1 (0.000s in global opts, 0.003s io_toposort) - 81 nodes - ('MergeOptimizer', 1) 13 - 0.031s 0 (0.000s in global opts, 0.003s io_toposort) - 81 nodes - times - times applied - nb node created - name: 0.263s - 15 - 0 - constant_folding 0.096s - 2 - 14 - local_greedy_distributor 0.066s - 4 - 19 - local_mul_canonizer 0.046s - 28 - 57 - local_fill_sink 0.042s - 35 - 78 - local_dimshuffle_lift 0.018s - 5 - 15 - local_upcast_elemwise_constant_inputs 0.010s - 11 - 4 - MergeOptimizer 0.009s - 4 - 0 - local_useless_elemwise 0.005s - 11 - 2 - local_fill_to_alloc 0.004s - 3 - 6 - local_neg_to_mul 0.002s - 1 - 3 - local_lift_transpose_through_dot 0.002s - 3 - 4 - local_shape_to_shape_i 0.002s - 2 - 4 - local_subtensor_lift 0.001s - 3 - 0 - local_subtensor_make_vector 0.001s - 1 - 1 - local_sum_all_to_none 0.131s - in 62 optimization that where not used (display only those with a runtime > 0) 0.050s - local_add_canonizer 0.018s - local_mul_zero 0.016s - local_one_minus_erf 0.010s - local_func_inv 0.006s - local_0_dot_x 0.005s - local_track_shape_i 0.004s - local_mul_switch_sink 0.004s - local_fill_cut 0.004s - local_one_minus_erf2 0.003s - local_remove_switch_const_cond 0.003s - local_cast_cast 0.002s - local_IncSubtensor_serialize 0.001s - local_sum_div_dimshuffle 0.001s - local_div_switch_sink 0.001s - local_dimshuffle_no_inplace_at_canonicalize 0.001s - local_cut_useless_reduce 0.001s - local_reduce_join 0.000s - local_sum_sum 0.000s - local_useless_alloc 0.000s - local_reshape_chain 0.000s - local_useless_subtensor 0.000s - local_reshape_lift 0.000s - local_flatten_lift 0.000s - local_useless_slice 0.000s - local_subtensor_of_alloc 0.000s - local_subtensor_of_dot 0.000s - local_subtensor_merge0.751816s - ('canonicalize', 'EquilibriumOptimizer', 4) - 0.004sThis line is fromSeqOptimizer, and indicates information related to a sub-optimizer. It means that this sub-optimizer took a total of .7s. Its name is'canonicalize'. It is anEquilibriumOptimizer. It was executed at index 4 by theSeqOptimizer. It spent 0.004s in the validate phase.All other lines are from the profiler of the
EquilibriumOptimizer.An
EquilibriumOptimizerdoes multiple passes on the Apply nodes from the graph, trying to apply local and global optimizations. Conceptually, it tries to execute all global optimizations, and to apply all local optimizations on all nodes in the graph. If no optimization got applied during a pass, it stops. So it tries to find an equilibrium state where none of the optimizations get applied. This is useful when we do not know a fixed order for the execution of the optimization.time 0.751s for 14 passesmeans that it took .7s and did 14 passes over the graph.nb nodes (start, end, max) 108 81 117means that at the start, the graph had 108 node, at the end, it had 81 and the maximum size was 117.Then it prints some global timing information: it spent 0.029s in
io_toposort, all local optimizers took 0.687s together for all passes, and global optimizers took a total of 0.010s.Then we print the timing for each pass, the optimization that got applied, and the number of time they got applied. For example, in pass 0, the
local_dimshuffle_liftoptimizer changed the graph 9 time.Then we print the time spent in each optimizer, the number of times they changed the graph and the number of nodes they introduced in the graph.
Optimizations with that pattern local_op_lift means that a node with that op will be replaced by another node, with the same op, but will do computation closer to the inputs of the graph. For instance,
local_op(f(x))getting replaced byf(local_op(x)).Optimization with that pattern local_op_sink is the opposite of lift. For instance
f(local_op(x))getting replaced bylocal_op(f(x)).Local optimizers can replace any arbitrary node in the graph, not only the node it received as input. For this, it must return a dict. The keys being nodes to replace and the values being the corresponding replacement.
This is useful to replace a client of the node received as parameter.
