Detailed Description

template<typename _Scalar, int _Rows, int _Cols, int _Options, int _MaxRows, int _MaxCols>
class Eigen::Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >

General-purpose arrays with easy API for coefficient-wise operations.

The Array class is very similar to the Matrix class. It provides general-purpose one- and two-dimensional arrays. The difference between the Array and the Matrix class is primarily in the API: the API for the Array class provides easy access to coefficient-wise operations, while the API for the Matrix class provides easy access to linear-algebra operations.

This class can be extended with the help of the plugin mechanism described on the page Customizing/Extending Eigen by defining the preprocessor symbol EIGEN_ARRAY_PLUGIN.

See Also: The Array class and coefficient-wise operations, The class hierarchy

Inheritance diagram for Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >:

Public Types
enum	{ RowsAtCompileTime, ColsAtCompileTime, SizeAtCompileTime, MaxRowsAtCompileTime, MaxColsAtCompileTime, MaxSizeAtCompileTime, IsVectorAtCompileTime, Flags, IsRowMajor , CoeffReadCost }

Public Member Functions
const CwiseUnaryOp < internal::scalar_abs_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	abs () const

const CwiseUnaryOp < internal::scalar_abs2_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	abs2 () const

const CwiseUnaryOp < internal::scalar_acos_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	acos () const

bool	all (void) const

bool	allFinite () const

bool	any (void) const

	Array ()

	Array (Index dim)

	Array (Index rows, Index cols)

	Array (const Scalar &val0, const Scalar &val1)

	Array (const Scalar &val0, const Scalar &val1, const Scalar &val2)

	Array (const Scalar &val0, const Scalar &val1, const Scalar &val2, const Scalar &val3)

template<typename OtherDerived >
	Array (const ArrayBase< OtherDerived > &other)

	Array (const Array &other)

template<typename OtherDerived >
	Array (const ReturnByValue< OtherDerived > &other)

template<typename OtherDerived >
	Array (const EigenBase< OtherDerived > &other)

const CwiseUnaryOp < internal::scalar_asin_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	asin () const

const CwiseBinaryOp < CustomBinaryOp, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	binaryExpr (const Eigen::ArrayBase< OtherDerived > &other, const CustomBinaryOp &func=CustomBinaryOp()) const

Block< Derived >	block (Index startRow, Index startCol, Index blockRows, Index blockCols)

const Block< const Derived >	block (Index startRow, Index startCol, Index blockRows, Index blockCols) const

template<int BlockRows, int BlockCols>
Block< Derived, BlockRows, BlockCols >	block (Index startRow, Index startCol)

template<int BlockRows, int BlockCols>
const Block< const Derived, BlockRows, BlockCols >	block (Index startRow, Index startCol) const

template<int BlockRows, int BlockCols>
Block< Derived, BlockRows, BlockCols >	block (Index startRow, Index startCol, Index blockRows, Index blockCols)

template<int BlockRows, int BlockCols>
const Block< const Derived, BlockRows, BlockCols >	block (Index startRow, Index startCol, Index blockRows, Index blockCols) const

Block< Derived >	bottomLeftCorner (Index cRows, Index cCols)

const Block< const Derived >	bottomLeftCorner (Index cRows, Index cCols) const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	bottomLeftCorner ()

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	bottomLeftCorner () const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	bottomLeftCorner (Index cRows, Index cCols)

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	bottomLeftCorner (Index cRows, Index cCols) const

Block< Derived >	bottomRightCorner (Index cRows, Index cCols)

const Block< const Derived >	bottomRightCorner (Index cRows, Index cCols) const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	bottomRightCorner ()

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	bottomRightCorner () const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	bottomRightCorner (Index cRows, Index cCols)

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	bottomRightCorner (Index cRows, Index cCols) const

RowsBlockXpr	bottomRows (Index n)

ConstRowsBlockXpr	bottomRows (Index n) const

template<int N>
NRowsBlockXpr< N >::Type	bottomRows (Index n=N)

template<int N>
ConstNRowsBlockXpr< N >::Type	bottomRows (Index n=N) const

internal::cast_return_type < Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const CwiseUnaryOp < internal::scalar_cast_op < typename internal::traits < Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::Scalar, NewType >, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > >::type	cast () const

ColXpr	col (Index i)

ConstColXpr	col (Index i) const

ConstColwiseReturnType	colwise () const

ColwiseReturnType	colwise ()

ConjugateReturnType	conjugate () const

void	conservativeResize (Index nbRows, Index nbCols)

void	conservativeResize (Index nbRows, NoChange_t)

void	conservativeResize (NoChange_t, Index nbCols)

void	conservativeResize (Index size)

void	conservativeResizeLike (const DenseBase< OtherDerived > &other)

const CwiseUnaryOp < internal::scalar_cos_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	cos () const

Index	count () const

const CwiseUnaryOp < internal::scalar_cube_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	cube () const

const CwiseUnaryOp < internal::scalar_abs_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	cwiseAbs () const

const CwiseUnaryOp < internal::scalar_abs2_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	cwiseAbs2 () const

const CwiseBinaryOp < std::equal_to< Scalar > , const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, const OtherDerived >	cwiseEqual (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseScalarEqualReturnType	cwiseEqual (const Scalar &s) const

const CwiseUnaryOp < internal::scalar_inverse_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	cwiseInverse () const

const CwiseBinaryOp < internal::scalar_max_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	cwiseMax (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseBinaryOp < internal::scalar_max_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const ConstantReturnType >	cwiseMax (const Scalar &other) const

const CwiseBinaryOp < internal::scalar_min_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	cwiseMin (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseBinaryOp < internal::scalar_min_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const ConstantReturnType >	cwiseMin (const Scalar &other) const

const CwiseBinaryOp < std::not_equal_to< Scalar > , const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, const OtherDerived >	cwiseNotEqual (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseBinaryOp < internal::scalar_product_op < typename Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >::Scalar, typename OtherDerived::Scalar > , const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, const OtherDerived >	cwiseProduct (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseBinaryOp < internal::scalar_quotient_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	cwiseQuotient (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseUnaryOp < internal::scalar_sqrt_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	cwiseSqrt () const

const Scalar *	data () const

Scalar *	data ()

EvalReturnType	eval () const

const CwiseUnaryOp < internal::scalar_exp_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	exp () const

void	fill (const Scalar &value)

template<unsigned int Added, unsigned int Removed>
const Flagged< Derived, Added, Removed >	flagged () const

const WithFormat< Derived >	format (const IOFormat &fmt) const

bool	hasNaN () const

SegmentReturnType	head (Index n)

ConstSegmentReturnType	head (Index n) const

template<int N>
FixedSegmentReturnType< N >::Type	head (Index n=N)

template<int N>
ConstFixedSegmentReturnType< N > ::Type	head (Index n=N) const

const ImagReturnType	imag () const

NonConstImagReturnType	imag ()

Index	innerSize () const

const CwiseUnaryOp < internal::scalar_inverse_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	inverse () const

template<typename OtherDerived >
bool	isApprox (const DenseBase< OtherDerived > &other, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const

bool	isApproxToConstant (const Scalar &value, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const

bool	isConstant (const Scalar &value, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const

template<typename Derived >
bool	isMuchSmallerThan (const typename NumTraits< Scalar >::Real &other, const RealScalar &prec) const

template<typename OtherDerived >
bool	isMuchSmallerThan (const DenseBase< OtherDerived > &other, const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const

bool	isOnes (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const

bool	isZero (const RealScalar &prec=NumTraits< Scalar >::dummy_precision()) const

Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > &	lazyAssign (const DenseBase< OtherDerived > &other)

ColsBlockXpr	leftCols (Index n)

ConstColsBlockXpr	leftCols (Index n) const

template<int N>
NColsBlockXpr< N >::Type	leftCols (Index n=N)

template<int N>
ConstNColsBlockXpr< N >::Type	leftCols (Index n=N) const

const CwiseUnaryOp < internal::scalar_log_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	log () const

MatrixWrapper< Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	matrix ()

const CwiseBinaryOp < internal::scalar_max_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	max (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseBinaryOp < internal::scalar_max_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const CwiseNullaryOp < internal::scalar_constant_op < Scalar >, PlainObject > >	max (const Scalar &other) const

internal::traits< Derived >::Scalar	maxCoeff () const

template<typename IndexType >
internal::traits< Derived >::Scalar	maxCoeff (IndexType row, IndexType col) const

template<typename IndexType >
internal::traits< Derived >::Scalar	maxCoeff (IndexType *index) const

Scalar	mean () const

ColsBlockXpr	middleCols (Index startCol, Index numCols)

ConstColsBlockXpr	middleCols (Index startCol, Index numCols) const

template<int N>
NColsBlockXpr< N >::Type	middleCols (Index startCol, Index n=N)

template<int N>
ConstNColsBlockXpr< N >::Type	middleCols (Index startCol, Index n=N) const

RowsBlockXpr	middleRows (Index startRow, Index n)

ConstRowsBlockXpr	middleRows (Index startRow, Index n) const

template<int N>
NRowsBlockXpr< N >::Type	middleRows (Index startRow, Index n=N)

template<int N>
ConstNRowsBlockXpr< N >::Type	middleRows (Index startRow, Index n=N) const

const CwiseBinaryOp < internal::scalar_min_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	min (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseBinaryOp < internal::scalar_min_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const CwiseNullaryOp < internal::scalar_constant_op < Scalar >, PlainObject > >	min (const Scalar &other) const

internal::traits< Derived >::Scalar	minCoeff () const

template<typename IndexType >
internal::traits< Derived >::Scalar	minCoeff (IndexType row, IndexType col) const

template<typename IndexType >
internal::traits< Derived >::Scalar	minCoeff (IndexType *index) const

const NestByValue< Derived >	nestByValue () const

Index	nonZeros () const

const CwiseBinaryOp < internal::scalar_boolean_and_op, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, const OtherDerived >	operator&& (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseBinaryOp < internal::scalar_product_op < typename Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >::Scalar, typename OtherDerived::Scalar > , const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, const OtherDerived >	operator* (const Eigen::ArrayBase< OtherDerived > &other) const

const ScalarMultipleReturnType	operator* (const Scalar &scalar) const

const CwiseUnaryOp < internal::scalar_multiple2_op < Scalar, std::complex< Scalar > >, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	operator* (const std::complex< Scalar > &scalar) const

const CwiseBinaryOp < internal::scalar_sum_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	operator+ (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseUnaryOp < internal::scalar_add_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	operator+ (const Scalar &scalar) const

const CwiseBinaryOp < internal::scalar_difference_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	operator- (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseUnaryOp < internal::scalar_opposite_op < typename internal::traits < Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	operator- () const

const CwiseUnaryOp < internal::scalar_add_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	operator- (const Scalar &scalar) const

const CwiseBinaryOp < internal::scalar_quotient_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived >	operator/ (const Eigen::ArrayBase< OtherDerived > &other) const

const CwiseUnaryOp < internal::scalar_quotient1_op < typename internal::traits < Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	operator/ (const Scalar &scalar) const

CommaInitializer< Derived >	operator<< (const Scalar &s)

template<typename OtherDerived >
CommaInitializer< Derived >	operator<< (const DenseBase< OtherDerived > &other)

template<typename OtherDerived >
Array &	operator= (const EigenBase< OtherDerived > &other)

template<typename OtherDerived >
Array &	operator= (const ArrayBase< OtherDerived > &other)

Array &	operator= (const Array &other)

const CwiseBinaryOp < internal::scalar_boolean_or_op, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, const OtherDerived >	operator\|\| (const Eigen::ArrayBase< OtherDerived > &other) const

Index	outerSize () const

const CwiseUnaryOp < internal::scalar_pow_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	pow (const Scalar &exponent) const

Scalar	prod () const

RealReturnType	real () const

NonConstRealReturnType	real ()

template<typename Func >
internal::result_of< Func(typename internal::traits< Derived > ::Scalar)>::type	redux (const Func &func) const

template<int RowFactor, int ColFactor>
const Replicate< Derived, RowFactor, ColFactor >	replicate () const

const ReplicateReturnType	replicate (Index rowFacor, Index colFactor) const

void	resize (Index nbRows, Index nbCols)

void	resize (Index size)

void	resize (NoChange_t, Index nbCols)

void	resize (Index nbRows, NoChange_t)

void	resizeLike (const EigenBase< OtherDerived > &_other)

ReverseReturnType	reverse ()

ConstReverseReturnType	reverse () const

void	reverseInPlace ()

ColsBlockXpr	rightCols (Index n)

ConstColsBlockXpr	rightCols (Index n) const

template<int N>
NColsBlockXpr< N >::Type	rightCols (Index n=N)

template<int N>
ConstNColsBlockXpr< N >::Type	rightCols (Index n=N) const

RowXpr	row (Index i)

ConstRowXpr	row (Index i) const

ConstRowwiseReturnType	rowwise () const

RowwiseReturnType	rowwise ()

SegmentReturnType	segment (Index start, Index n)

ConstSegmentReturnType	segment (Index start, Index n) const

template<int N>
FixedSegmentReturnType< N >::Type	segment (Index start, Index n=N)

template<int N>
ConstFixedSegmentReturnType< N > ::Type	segment (Index start, Index n=N) const

template<typename ThenDerived , typename ElseDerived >
const Select< Derived, ThenDerived, ElseDerived >	select (const DenseBase< ThenDerived > &thenMatrix, const DenseBase< ElseDerived > &elseMatrix) const

template<typename ThenDerived >
const Select< Derived, ThenDerived, typename ThenDerived::ConstantReturnType >	select (const DenseBase< ThenDerived > &thenMatrix, const typename ThenDerived::Scalar &elseScalar) const

template<typename ElseDerived >
const Select< Derived, typename ElseDerived::ConstantReturnType, ElseDerived >	select (const typename ElseDerived::Scalar &thenScalar, const DenseBase< ElseDerived > &elseMatrix) const

Derived &	setConstant (const Scalar &value)

Derived &	setLinSpaced (Index size, const Scalar &low, const Scalar &high)
	Sets a linearly space vector. More...

Derived &	setLinSpaced (const Scalar &low, const Scalar &high)
	Sets a linearly space vector. More...

Derived &	setOnes ()

Derived &	setRandom ()

Derived &	setZero ()

const CwiseUnaryOp < internal::scalar_sin_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	sin () const

const CwiseUnaryOp < internal::scalar_sqrt_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	sqrt () const

const CwiseUnaryOp < internal::scalar_square_op < Scalar >, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	square () const

Scalar	sum () const

template<typename OtherDerived >
void	swap (ArrayBase< OtherDerived > const &other)

template<typename OtherDerived >
void	swap (const DenseBase< OtherDerived > &other, int=OtherDerived::ThisConstantIsPrivateInPlainObjectBase)

template<typename OtherDerived >
void	swap (PlainObjectBase< OtherDerived > &other)

SegmentReturnType	tail (Index n)

ConstSegmentReturnType	tail (Index n) const

template<int N>
FixedSegmentReturnType< N >::Type	tail (Index n=N)

template<int N>
ConstFixedSegmentReturnType< N > ::Type	tail (Index n=N) const

const CwiseUnaryOp < internal::scalar_tan_op < Scalar >, Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	tan () const

Block< Derived >	topLeftCorner (Index cRows, Index cCols)

const Block< const Derived >	topLeftCorner (Index cRows, Index cCols) const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	topLeftCorner ()

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	topLeftCorner () const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	topLeftCorner (Index cRows, Index cCols)

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	topLeftCorner (Index cRows, Index cCols) const

Block< Derived >	topRightCorner (Index cRows, Index cCols)

const Block< const Derived >	topRightCorner (Index cRows, Index cCols) const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	topRightCorner ()

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	topRightCorner () const

template<int CRows, int CCols>
Block< Derived, CRows, CCols >	topRightCorner (Index cRows, Index cCols)

template<int CRows, int CCols>
const Block< const Derived, CRows, CCols >	topRightCorner (Index cRows, Index cCols) const

RowsBlockXpr	topRows (Index n)

ConstRowsBlockXpr	topRows (Index n) const

template<int N>
NRowsBlockXpr< N >::Type	topRows (Index n=N)

template<int N>
ConstNRowsBlockXpr< N >::Type	topRows (Index n=N) const

Eigen::Transpose< Derived >	transpose ()

ConstTransposeReturnType	transpose () const

void	transposeInPlace ()

const CwiseUnaryOp < CustomUnaryOp, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	unaryExpr (const CustomUnaryOp &func=CustomUnaryOp()) const
	Apply a unary operator coefficient-wise. More...

const CwiseUnaryView < CustomViewOp, const Array < _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >	unaryViewExpr (const CustomViewOp &func=CustomViewOp()) const

CoeffReturnType	value () const

template<typename Visitor >
void	visit (Visitor &func) const

Static Public Member Functions
static const ConstantReturnType	Constant (Index rows, Index cols, const Scalar &value)

static const ConstantReturnType	Constant (Index size, const Scalar &value)

static const ConstantReturnType	Constant (const Scalar &value)

static const SequentialLinSpacedReturnType	LinSpaced (Sequential_t, Index size, const Scalar &low, const Scalar &high)
	Sets a linearly space vector. More...

static const RandomAccessLinSpacedReturnType	LinSpaced (Index size, const Scalar &low, const Scalar &high)
	Sets a linearly space vector. More...

static const SequentialLinSpacedReturnType	LinSpaced (Sequential_t, const Scalar &low, const Scalar &high)
	Sets a linearly space vector. More...

static const RandomAccessLinSpacedReturnType	LinSpaced (const Scalar &low, const Scalar &high)
	Sets a linearly space vector. More...

template<typename CustomNullaryOp >
static const CwiseNullaryOp < CustomNullaryOp, Derived >	NullaryExpr (Index rows, Index cols, const CustomNullaryOp &func)

template<typename CustomNullaryOp >
static const CwiseNullaryOp < CustomNullaryOp, Derived >	NullaryExpr (Index size, const CustomNullaryOp &func)

template<typename CustomNullaryOp >
static const CwiseNullaryOp < CustomNullaryOp, Derived >	NullaryExpr (const CustomNullaryOp &func)

static const ConstantReturnType	Ones (Index rows, Index cols)

static const ConstantReturnType	Ones (Index size)

static const ConstantReturnType	Ones ()

static const CwiseNullaryOp < internal::scalar_random_op < Scalar >, Derived >	Random (Index rows, Index cols)

static const CwiseNullaryOp < internal::scalar_random_op < Scalar >, Derived >	Random (Index size)

static const CwiseNullaryOp < internal::scalar_random_op < Scalar >, Derived >	Random ()

static const ConstantReturnType	Zero (Index rows, Index cols)

static const ConstantReturnType	Zero (Index size)

static const ConstantReturnType	Zero ()

Map
These are convenience functions returning Map objects. The Map() static functions return unaligned Map objects, while the AlignedMap() functions return aligned Map objects and thus should be called only with 16-byte-aligned data pointers. See Also class Map
static ConstMapType	Map (const Scalar *data)

static MapType	Map (Scalar *data)

static ConstMapType	Map (const Scalar *data, Index size)

static MapType	Map (Scalar *data, Index size)

static ConstMapType	Map (const Scalar *data, Index rows, Index cols)

static MapType	Map (Scalar *data, Index rows, Index cols)

static StridedConstMapType < Stride< Outer, Inner > >::type	Map (const Scalar *data, const Stride< Outer, Inner > &stride)

static StridedMapType< Stride < Outer, Inner > >::type	Map (Scalar *data, const Stride< Outer, Inner > &stride)

static StridedConstMapType < Stride< Outer, Inner > >::type	Map (const Scalar *data, Index size, const Stride< Outer, Inner > &stride)

static StridedMapType< Stride < Outer, Inner > >::type	Map (Scalar *data, Index size, const Stride< Outer, Inner > &stride)

static StridedConstMapType < Stride< Outer, Inner > >::type	Map (const Scalar *data, Index rows, Index cols, const Stride< Outer, Inner > &stride)

static StridedMapType< Stride < Outer, Inner > >::type	Map (Scalar *data, Index rows, Index cols, const Stride< Outer, Inner > &stride)

static ConstAlignedMapType	MapAligned (const Scalar *data)

static AlignedMapType	MapAligned (Scalar *data)

static ConstAlignedMapType	MapAligned (const Scalar *data, Index size)

static AlignedMapType	MapAligned (Scalar *data, Index size)

static ConstAlignedMapType	MapAligned (const Scalar *data, Index rows, Index cols)

static AlignedMapType	MapAligned (Scalar *data, Index rows, Index cols)

static StridedConstAlignedMapType < Stride< Outer, Inner > >::type	MapAligned (const Scalar *data, const Stride< Outer, Inner > &stride)

static StridedAlignedMapType < Stride< Outer, Inner > >::type	MapAligned (Scalar *data, const Stride< Outer, Inner > &stride)

static StridedConstAlignedMapType < Stride< Outer, Inner > >::type	MapAligned (const Scalar *data, Index size, const Stride< Outer, Inner > &stride)

static StridedAlignedMapType < Stride< Outer, Inner > >::type	MapAligned (Scalar *data, Index size, const Stride< Outer, Inner > &stride)

static StridedConstAlignedMapType < Stride< Outer, Inner > >::type	MapAligned (const Scalar *data, Index rows, Index cols, const Stride< Outer, Inner > &stride)

static StridedAlignedMapType < Stride< Outer, Inner > >::type	MapAligned (Scalar *data, Index rows, Index cols, const Stride< Outer, Inner > &stride)

Protected Member Functions
Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > &	_set (const DenseBase< OtherDerived > &other)
	Copies the value of the expression other into `*this` with automatic resizing. More...

Related Functions
(Note that these are not member functions.)
template<typename Derived >
std::ostream &	operator<< (std::ostream &s, const DenseBase< Derived > &m)

Member Enumeration Documentation

anonymous enum

inherited

Enumerator
RowsAtCompileTime	The number of rows at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant. See Also MatrixBase::rows(), MatrixBase::cols(), ColsAtCompileTime, SizeAtCompileTime
ColsAtCompileTime	The number of columns at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant. See Also MatrixBase::rows(), MatrixBase::cols(), RowsAtCompileTime, SizeAtCompileTime
SizeAtCompileTime	This is equal to the number of coefficients, i.e. the number of rows times the number of columns, or to Dynamic if this is not known at compile-time. See Also RowsAtCompileTime, ColsAtCompileTime
MaxRowsAtCompileTime	This value is equal to the maximum possible number of rows that this expression might have. If this expression might have an arbitrarily high number of rows, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. See Also RowsAtCompileTime, MaxColsAtCompileTime, MaxSizeAtCompileTime
MaxColsAtCompileTime	This value is equal to the maximum possible number of columns that this expression might have. If this expression might have an arbitrarily high number of columns, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. See Also ColsAtCompileTime, MaxRowsAtCompileTime, MaxSizeAtCompileTime
MaxSizeAtCompileTime	This value is equal to the maximum possible number of coefficients that this expression might have. If this expression might have an arbitrarily high number of coefficients, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. See Also SizeAtCompileTime, MaxRowsAtCompileTime, MaxColsAtCompileTime
IsVectorAtCompileTime	This is set to true if either the number of rows or the number of columns is known at compile-time to be equal to 1. Indeed, in that case, we are dealing with a column-vector (if there is only one column) or with a row-vector (if there is only one row).
Flags	This stores expression Flags flags which may or may not be inherited by new expressions constructed from this one. See the list of flags.
IsRowMajor	True if this expression has row-major storage order.
CoeffReadCost	This is a rough measure of how expensive it is to read one coefficient from this expression.

Constructor & Destructor Documentation

Array ( )

inline

Default constructor.

For fixed-size matrices, does nothing.

For dynamic-size matrices, creates an empty matrix of size 0. Does not allocate any array. Such a matrix is called a null matrix. This constructor is the unique way to create null matrices: resizing a matrix to 0 is not supported.

See Also: resize(Index,Index)

Array ( Index dim )

inlineexplicit

Constructs a vector or row-vector with given dimension. This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Note that this is only useful for dynamic-size vectors. For fixed-size vectors, it is redundant to pass the dimension here, so it makes more sense to use the default constructor Matrix() instead.

Array	(	Index	rows,
		Index	cols
	)

constructs an uninitialized matrix with rows rows and cols columns.

This is useful for dynamic-size matrices. For fixed-size matrices, it is redundant to pass these parameters, so one should use the default constructor Matrix() instead.

Array	(	const Scalar &	val0,
		const Scalar &	val1
	)

constructs an initialized 2D vector with given coefficients

Array	(	const Scalar &	val0,
		const Scalar &	val1,
		const Scalar &	val2
	)

inline

constructs an initialized 3D vector with given coefficients

Array	(	const Scalar &	val0,
		const Scalar &	val1,
		const Scalar &	val2,
		const Scalar &	val3
	)

inline

constructs an initialized 4D vector with given coefficients

Array ( const ArrayBase< OtherDerived > & other )

inline

Constructor copying the value of the expression other

Array ( const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > & other )

inline

Copy constructor

Array ( const ReturnByValue< OtherDerived > & other )

inline

Copy constructor with in-place evaluation

Array ( const EigenBase< OtherDerived > & other )

inline

See Also: MatrixBase::operator=(const EigenBase<OtherDerived>&)

Member Function Documentation

Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > & _set ( const DenseBase< OtherDerived > & other )

inlineprotectedinherited

Copies the value of the expression other into *this with automatic resizing.

*this might be resized to match the dimensions of other. If *this was a null matrix (not already initialized), it will be initialized.

Note that copying a row-vector into a vector (and conversely) is allowed. The resizing, if any, is then done in the appropriate way so that row-vectors remain row-vectors and vectors remain vectors.

See Also: operator=(const MatrixBase<OtherDerived>&), _set_noalias()

const CwiseUnaryOp<internal::scalar_abs_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > abs ( ) const

inlineinherited

Returns: an expression of the coefficient-wise absolute value of *this

Example:

Array3d v(1,-2,-3);

cout << v.abs() << endl;

Output:

1
2
3

See Also: abs2()

const CwiseUnaryOp<internal::scalar_abs2_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > abs2 ( ) const

inlineinherited

Returns: an expression of the coefficient-wise squared absolute value of *this

Example:

Array3d v(1,-2,-3);

cout << v.abs2() << endl;

Output:

1
4
9

See Also: abs(), square()

const CwiseUnaryOp<internal::scalar_acos_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > acos ( ) const

inlineinherited

Returns: an expression of the coefficient-wise arc cosine of *this.

Example:

Array3d v(0, sqrt(2.)/2, 1);

cout << v.acos() << endl;

Output:

 1.57
0.785
    0

See Also: cos(), asin()

bool all ( void ) const

inlineinherited

Returns: true if all coefficients are true

Example:

Vector3f boxMin(Vector3f::Zero()), boxMax(Vector3f::Ones());
Vector3f p0 = Vector3f::Random(), p1 = Vector3f::Random().cwiseAbs();
// let's check if p0 and p1 are inside the axis aligned box defined by the corners boxMin,boxMax:
cout << "Is (" << p0.transpose() << ") inside the box: "
     << ((boxMin.array()<p0.array()).all() && (boxMax.array()>p0.array()).all()) << endl;
cout << "Is (" << p1.transpose() << ") inside the box: "
     << ((boxMin.array()<p1.array()).all() && (boxMax.array()>p1.array()).all()) << endl;

Output:

Is (  0.68 -0.211  0.566) inside the box: 0
Is (0.597 0.823 0.605) inside the box: 1

See Also: any(), Cwise::operator<()

References Eigen::Dynamic.

bool allFinite ( ) const

inlineinherited

Returns: true if *this contains only finite numbers, i.e., no NaN and no +/-INF values.

See Also: hasNaN()

bool any ( void ) const

inlineinherited

Returns: true if at least one coefficient is true

See Also: all()

References Eigen::Dynamic.

const CwiseUnaryOp<internal::scalar_asin_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > asin ( ) const

inlineinherited

Returns: an expression of the coefficient-wise arc sine of *this.

Example:

Array3d v(0, sqrt(2.)/2, 1);

cout << v.asin() << endl;

Output:

    0
0.785
 1.57

See Also: sin(), acos()

const CwiseBinaryOp<CustomBinaryOp, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> binaryExpr	(	const Eigen::ArrayBase< OtherDerived > &	other,
		const CustomBinaryOp &	func = `CustomBinaryOp()`
	)		const

inlineinherited

Returns: an expression of a custom coefficient-wise operator func of *this and other

The template parameter CustomBinaryOp is the type of the functor of the custom operator (see class CwiseBinaryOp for an example)

Here is an example illustrating the use of custom functors:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
// define a custom template binary functor
template<typename Scalar> struct MakeComplexOp {
  EIGEN_EMPTY_STRUCT_CTOR(MakeComplexOp)
  typedef complex<Scalar> result_type;
  complex<Scalar> operator()(const Scalar& a, const Scalar& b) const { return complex<Scalar>(a,b); }
};
int main(int, char**)
{
  Matrix4d m1 = Matrix4d::Random(), m2 = Matrix4d::Random();
  cout << m1.binaryExpr(m2, MakeComplexOp<double>()) << endl;
  return 0;
}

Output:

   (0.68,0.271)  (0.823,-0.967) (-0.444,-0.687)   (-0.27,0.998)
 (-0.211,0.435) (-0.605,-0.514)  (0.108,-0.198) (0.0268,-0.563)
 (0.566,-0.717)  (-0.33,-0.726) (-0.0452,-0.74)  (0.904,0.0259)
  (0.597,0.214)   (0.536,0.608)  (0.258,-0.782)   (0.832,0.678)

See Also: class CwiseBinaryOp, operator+(), operator-(), cwiseProduct()

Block<Derived> block	(	Index	startRow,
		Index	startCol,
		Index	blockRows,
		Index	blockCols
	)

inlineinherited

Returns: a dynamic-size expression of a block in *this.

Parameters

startRow	the first row in the block
startCol	the first column in the block
blockRows	the number of rows in the block
blockCols	the number of columns in the block

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.block(1, 1, 2, 2):" << endl << m.block(1, 1, 2, 2) << endl;
m.block(1, 1, 2, 2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.block(1, 1, 2, 2):
-6  1
-3  0
Now the matrix m is:
 7  9 -5 -3
-2  0  0  0
 6  0  0  9
 6  6  3  9

Note: Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size matrix, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.

See Also: class Block, block(Index,Index)

const Block<const Derived> block	(	Index	startRow,
		Index	startCol,
		Index	blockRows,
		Index	blockCols
	)		const

inlineinherited

This is the const version of block(Index,Index,Index,Index).

Block<Derived, BlockRows, BlockCols> block	(	Index	startRow,
		Index	startCol
	)

inlineinherited

Returns: a fixed-size expression of a block in *this.

The template parameters BlockRows and BlockCols are the number of rows and columns in the block.

Parameters

startRow	the first row in the block
startCol	the first column in the block

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.block<2,2>(1,1):" << endl << m.block<2,2>(1,1) << endl;
m.block<2,2>(1,1).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.block<2,2>(1,1):
-6  1
-3  0
Now the matrix m is:
 7  9 -5 -3
-2  0  0  0
 6  0  0  9
 6  6  3  9

Note: since block is a templated member, the keyword template has to be used if the matrix type is also a template parameter:
m.template block<3,3>(1,1);

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived, BlockRows, BlockCols> block	(	Index	startRow,
		Index	startCol
	)		const

inlineinherited

This is the const version of block<>(Index, Index).

Block<Derived, BlockRows, BlockCols> block	(	Index	startRow,
		Index	startCol,
		Index	blockRows,
		Index	blockCols
	)

inlineinherited

Returns: an expression of a block in *this.

Template Parameters

BlockRows	number of rows in block as specified at compile-time
BlockCols	number of columns in block as specified at compile-time

Parameters

startRow	the first row in the block
startCol	the first column in the block
blockRows	number of rows in block as specified at run-time
blockCols	number of columns in block as specified at run-time

This function is mainly useful for blocks where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, blockRows should equal BlockRows unless BlockRows is Dynamic, and the same for the number of columns.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the block:" << endl << m.block<2, Dynamic>(1, 1, 2, 3) << endl;
m.block<2, Dynamic>(1, 1, 2, 3).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the block:" << endl << m.block<2, Dynamic>(1, 1, 2, 3) << endl;
m.block<2, Dynamic>(1, 1, 2, 3).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived, BlockRows, BlockCols> block	(	Index	startRow,
		Index	startCol,
		Index	blockRows,
		Index	blockCols
	)		const

inlineinherited

This is the const version of block<>(Index, Index, Index, Index).

Block<Derived> bottomLeftCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: a dynamic-size expression of a bottom-left corner of *this.

Parameters

cRows	the number of rows in the corner
cCols	the number of columns in the corner

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.bottomLeftCorner(2, 2):" << endl;
cout << m.bottomLeftCorner(2, 2) << endl;
m.bottomLeftCorner(2, 2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.bottomLeftCorner(2, 2):
 6 -3
 6  6
Now the matrix m is:
 7  9 -5 -3
-2 -6  1  0
 0  0  0  9
 0  0  3  9

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived> bottomLeftCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of bottomLeftCorner(Index, Index).

Block<Derived, CRows, CCols> bottomLeftCorner ( )

inlineinherited

Returns: an expression of a fixed-size bottom-left corner of *this.

The template parameters CRows and CCols are the number of rows and columns in the corner.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.bottomLeftCorner<2,2>():" << endl;
cout << m.bottomLeftCorner<2,2>() << endl;
m.bottomLeftCorner<2,2>().setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.bottomLeftCorner<2,2>():
 6 -3
 6  6
Now the matrix m is:
 7  9 -5 -3
-2 -6  1  0
 0  0  0  9
 0  0  3  9

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived, CRows, CCols> bottomLeftCorner ( ) const

inlineinherited

This is the const version of bottomLeftCorner<int, int>().

Block<Derived, CRows, CCols> bottomLeftCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: an expression of a bottom-left corner of *this.

Template Parameters

CRows	number of rows in corner as specified at compile-time
CCols	number of columns in corner as specified at compile-time

Parameters

cRows	number of rows in corner as specified at run-time
cCols	number of columns in corner as specified at run-time

This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.bottomLeftCorner<2,Dynamic>(2,2):" << endl;
cout << m.bottomLeftCorner<2,Dynamic>(2,2) << endl;
m.bottomLeftCorner<2,Dynamic>(2,2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.bottomLeftCorner<2,Dynamic>(2,2):
 6 -3
 6  6
Now the matrix m is:
 7  9 -5 -3
-2 -6  1  0
 0  0  0  9
 0  0  3  9

See Also: class Block

const Block<const Derived, CRows, CCols> bottomLeftCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of bottomLeftCorner<int, int>(Index, Index).

Block<Derived> bottomRightCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: a dynamic-size expression of a bottom-right corner of *this.

Parameters

cRows	the number of rows in the corner
cCols	the number of columns in the corner

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.bottomRightCorner(2, 2):" << endl;
cout << m.bottomRightCorner(2, 2) << endl;
m.bottomRightCorner(2, 2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.bottomRightCorner(2, 2):
0 9
3 9
Now the matrix m is:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  0
 6  6  0  0

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived> bottomRightCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of bottomRightCorner(Index, Index).

Block<Derived, CRows, CCols> bottomRightCorner ( )

inlineinherited

Returns: an expression of a fixed-size bottom-right corner of *this.

The template parameters CRows and CCols are the number of rows and columns in the corner.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.bottomRightCorner<2,2>():" << endl;
cout << m.bottomRightCorner<2,2>() << endl;
m.bottomRightCorner<2,2>().setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.bottomRightCorner<2,2>():
0 9
3 9
Now the matrix m is:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  0
 6  6  0  0

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived, CRows, CCols> bottomRightCorner ( ) const

inlineinherited

This is the const version of bottomRightCorner<int, int>().

Block<Derived, CRows, CCols> bottomRightCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: an expression of a bottom-right corner of *this.

Template Parameters

CRows	number of rows in corner as specified at compile-time
CCols	number of columns in corner as specified at compile-time

Parameters

cRows	number of rows in corner as specified at run-time
cCols	number of columns in corner as specified at run-time

This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.bottomRightCorner<2,Dynamic>(2,2):" << endl;
cout << m.bottomRightCorner<2,Dynamic>(2,2) << endl;
m.bottomRightCorner<2,Dynamic>(2,2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.bottomRightCorner<2,Dynamic>(2,2):
0 9
3 9
Now the matrix m is:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  0
 6  6  0  0

See Also: class Block

const Block<const Derived, CRows, CCols> bottomRightCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of bottomRightCorner<int, int>(Index, Index).

RowsBlockXpr bottomRows ( Index n )

inlineinherited

Returns: a block consisting of the bottom rows of *this.

Parameters

n	the number of rows in the block

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.bottomRows(2):" << endl;
cout << a.bottomRows(2) << endl;
a.bottomRows(2).setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.bottomRows(2):
 6 -3  0  9
 6  6  3  9
Now the array a is:
 7  9 -5 -3
-2 -6  1  0
 0  0  0  0
 0  0  0  0

See Also: class Block, block(Index,Index,Index,Index)

ConstRowsBlockXpr bottomRows ( Index n ) const

inlineinherited

This is the const version of bottomRows(Index).

NRowsBlockXpr<N>::Type bottomRows ( Index n = N )

inlineinherited

Returns: a block consisting of the bottom rows of *this.

Template Parameters

N	the number of rows in the block as specified at compile-time

Parameters

n	the number of rows in the block as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.bottomRows<2>():" << endl;
cout << a.bottomRows<2>() << endl;
a.bottomRows<2>().setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.bottomRows<2>():
 6 -3  0  9
 6  6  3  9
Now the array a is:
 7  9 -5 -3
-2 -6  1  0
 0  0  0  0
 0  0  0  0

See Also: class Block, block(Index,Index,Index,Index)

ConstNRowsBlockXpr<N>::Type bottomRows ( Index n = N ) const

inlineinherited

This is the const version of bottomRows<int>().

internal::cast_return_type<Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > ,const CwiseUnaryOp<internal::scalar_cast_op<typename internal::traits<Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::Scalar, NewType>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > >::type cast ( ) const

inlineinherited

Returns: an expression of *this with the Scalar type casted to NewScalar.

The template parameter NewScalar is the type we are casting the scalars to.

See Also: class CwiseUnaryOp

ColXpr col ( Index i )

inlineinherited

Returns: an expression of the i-th column of *this. Note that the numbering starts at 0.

Example:

Matrix3d m = Matrix3d::Identity();
m.col(1) = Vector3d(4,5,6);
cout << m << endl;

Output:

1 4 0
0 5 0
0 6 1

See Also: row(), class Block

Referenced by VectorwiseOp< ExpressionType, Direction >::cross().

ConstColXpr col ( Index i ) const

inlineinherited

This is the const version of col().

const DenseBase< Derived >::ConstColwiseReturnType colwise ( ) const

inlineinherited

Returns: a VectorwiseOp wrapper of *this providing additional partial reduction operations

Example:

Matrix3d m = Matrix3d::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the sum of each column:" << endl << m.colwise().sum() << endl;
cout << "Here is the maximum absolute value of each column:"
     << endl << m.cwiseAbs().colwise().maxCoeff() << endl;

Output:

Here is the matrix m:
  0.68  0.597  -0.33
-0.211  0.823  0.536
 0.566 -0.605 -0.444
Here is the sum of each column:
  1.04  0.815 -0.238
Here is the maximum absolute value of each column:
 0.68 0.823 0.536

See Also: rowwise(), class VectorwiseOp, Reductions, visitors and broadcasting

Referenced by Eigen::umeyama().

DenseBase< Derived >::ColwiseReturnType colwise ( )

inlineinherited

Returns: a writable VectorwiseOp wrapper of *this providing additional partial reduction operations

See Also: rowwise(), class VectorwiseOp, Reductions, visitors and broadcasting

ConjugateReturnType conjugate ( ) const

inlineinherited

Returns: an expression of the complex conjugate of *this.

See Also: adjoint()

void conservativeResize	(	Index	nbRows,
		Index	nbCols
	)

inlineinherited

Resizes the matrix to rows x cols while leaving old values untouched.

The method is intended for matrices of dynamic size. If you only want to change the number of rows and/or of columns, you can use conservativeResize(NoChange_t, Index) or conservativeResize(Index, NoChange_t).

Matrices are resized relative to the top-left element. In case values need to be appended to the matrix they will be uninitialized.

void conservativeResize	(	Index	nbRows,
		NoChange_t
	)

inlineinherited

Resizes the matrix to rows x cols while leaving old values untouched.

As opposed to conservativeResize(Index rows, Index cols), this version leaves the number of columns unchanged.

In case the matrix is growing, new rows will be uninitialized.

void conservativeResize	(	NoChange_t	,
		Index	nbCols
	)

inlineinherited

Resizes the matrix to rows x cols while leaving old values untouched.

As opposed to conservativeResize(Index rows, Index cols), this version leaves the number of rows unchanged.

In case the matrix is growing, new columns will be uninitialized.

void conservativeResize ( Index size )

inlineinherited

Resizes the vector to size while retaining old values.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.. This method does not work for partially dynamic matrices when the static dimension is anything other than 1. For example it will not work with Matrix<double, 2, Dynamic>.

When values are appended, they will be uninitialized.

void conservativeResizeLike ( const DenseBase< OtherDerived > & other )

inlineinherited

Resizes the matrix to rows x cols of other, while leaving old values untouched.

The method is intended for matrices of dynamic size. If you only want to change the number of rows and/or of columns, you can use conservativeResize(NoChange_t, Index) or conservativeResize(Index, NoChange_t).

Matrices are resized relative to the top-left element. In case values need to be appended to the matrix they will copied from other.

const DenseBase< Derived >::ConstantReturnType Constant	(	Index	nbRows,
		Index	nbCols,
		const Scalar &	value
	)

inlinestaticinherited

Returns: an expression of a constant matrix of value value

The parameters nbRows and nbCols are the number of rows and of columns of the returned matrix. Must be compatible with this DenseBase type.

This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass nbRows and nbCols as arguments, so Zero() should be used instead.

The template parameter CustomNullaryOp is the type of the functor.

See Also: class CwiseNullaryOp

References DenseBase< Derived >::NullaryExpr().

const DenseBase< Derived >::ConstantReturnType Constant	(	Index	size,
		const Scalar &	value
	)

inlinestaticinherited

Returns: an expression of a constant matrix of value value

The parameter size is the size of the returned vector. Must be compatible with this DenseBase type.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.

The template parameter CustomNullaryOp is the type of the functor.

See Also: class CwiseNullaryOp

References DenseBase< Derived >::NullaryExpr().

const DenseBase< Derived >::ConstantReturnType Constant ( const Scalar & value )

inlinestaticinherited

Returns: an expression of a constant matrix of value value

This variant is only for fixed-size DenseBase types. For dynamic-size types, you need to use the variants taking size arguments.

The template parameter CustomNullaryOp is the type of the functor.

See Also: class CwiseNullaryOp

References DenseBase< Derived >::NullaryExpr().

const CwiseUnaryOp<internal::scalar_cos_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > cos ( ) const

inlineinherited

Returns: an expression of the coefficient-wise cosine of *this.

Example:

Array3d v(M_PI, M_PI/2, M_PI/3);

cout << v.cos() << endl;

Output:

      -1
6.12e-17
     0.5

See Also: sin(), acos()

DenseBase< Derived >::Index count ( ) const

inlineinherited

Returns: the number of coefficients which evaluate to true

See Also: all(), any()

const CwiseUnaryOp<internal::scalar_cube_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > cube ( ) const

inlineinherited

Returns: an expression of the coefficient-wise cube of *this.

Example:

Array3d v(2,3,4);

cout << v.cube() << endl;

Output:

 8
27
64

See Also: square(), pow()

const CwiseUnaryOp<internal::scalar_abs_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > cwiseAbs ( ) const

inlineinherited

Returns: an expression of the coefficient-wise absolute value of *this

Example:

MatrixXd m(2,3);
m << 2, -4, 6,   
     -5, 1, 0;
cout << m.cwiseAbs() << endl;

Output:

2 4 6
5 1 0

See Also: cwiseAbs2()

const CwiseUnaryOp<internal::scalar_abs2_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > cwiseAbs2 ( ) const

inlineinherited

Returns: an expression of the coefficient-wise squared absolute value of *this

Example:

MatrixXd m(2,3);
m << 2, -4, 6,   
     -5, 1, 0;
cout << m.cwiseAbs2() << endl;

Output:

 4 16 36
25  1  0

See Also: cwiseAbs()

const CwiseBinaryOp<std::equal_to<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> cwiseEqual ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient-wise == operator of *this and other

Warning: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

Example:

MatrixXi m(2,2);
m << 1, 0,
     1, 1;
cout << "Comparing m with identity matrix:" << endl;
cout << m.cwiseEqual(MatrixXi::Identity(2,2)) << endl;
int count = m.cwiseEqual(MatrixXi::Identity(2,2)).count();
cout << "Number of coefficients that are equal: " << count << endl;

Output:

Comparing m with identity matrix:
1 1
0 1
Number of coefficients that are equal: 3

See Also: cwiseNotEqual(), isApprox(), isMuchSmallerThan()

const CwiseScalarEqualReturnType cwiseEqual ( const Scalar & s ) const

inlineinherited

Returns: an expression of the coefficient-wise == operator of *this and a scalar s

Warning: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

See Also: cwiseEqual(const MatrixBase<OtherDerived> &) const

const CwiseUnaryOp<internal::scalar_inverse_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > cwiseInverse ( ) const

inlineinherited

Returns: an expression of the coefficient-wise inverse of *this.

Example:

MatrixXd m(2,3);
m << 2, 0.5, 1,   
     3, 0.25, 1;
cout << m.cwiseInverse() << endl;

Output:

  0.5     2     1
0.333     4     1

See Also: cwiseProduct()

const CwiseBinaryOp<internal::scalar_max_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> cwiseMax ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient-wise max of *this and other

Example:

Vector3d v(2,3,4), w(4,2,3);

cout << v.cwiseMax(w) << endl;

Output:

4
3
4

See Also: class CwiseBinaryOp, min()

const CwiseBinaryOp<internal::scalar_max_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const ConstantReturnType> cwiseMax ( const Scalar & other ) const

inlineinherited

Returns: an expression of the coefficient-wise max of *this and scalar other

See Also: class CwiseBinaryOp, min()

const CwiseBinaryOp<internal::scalar_min_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> cwiseMin ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient-wise min of *this and other

Example:

Vector3d v(2,3,4), w(4,2,3);

cout << v.cwiseMin(w) << endl;

Output:

2
2
3

See Also: class CwiseBinaryOp, max()

const CwiseBinaryOp<internal::scalar_min_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const ConstantReturnType> cwiseMin ( const Scalar & other ) const

inlineinherited

Returns: an expression of the coefficient-wise min of *this and scalar other

See Also: class CwiseBinaryOp, min()

const CwiseBinaryOp<std::not_equal_to<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> cwiseNotEqual ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient-wise != operator of *this and other

Warning: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

Example:

MatrixXi m(2,2);
m << 1, 0,
     1, 1;
cout << "Comparing m with identity matrix:" << endl;
cout << m.cwiseNotEqual(MatrixXi::Identity(2,2)) << endl;
int count = m.cwiseNotEqual(MatrixXi::Identity(2,2)).count();
cout << "Number of coefficients that are not equal: " << count << endl;

Output:

Comparing m with identity matrix:
0 0
1 0
Number of coefficients that are not equal: 1

See Also: cwiseEqual(), isApprox(), isMuchSmallerThan()

const CwiseBinaryOp<internal::scalar_product_op<typename Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > ::Scalar, typename OtherDerived ::Scalar >, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived > cwiseProduct ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the Schur product (coefficient wise product) of *this and other

Example:

Matrix3i a = Matrix3i::Random(), b = Matrix3i::Random();
Matrix3i c = a.cwiseProduct(b);
cout << "a:\n" << a << "\nb:\n" << b << "\nc:\n" << c << endl;

Output:

See Also: class CwiseBinaryOp, cwiseAbs2

const CwiseBinaryOp<internal::scalar_quotient_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> cwiseQuotient ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient-wise quotient of *this and other

Example:

Vector3d v(2,3,4), w(4,2,3);

cout << v.cwiseQuotient(w) << endl;

Output:

 0.5
 1.5
1.33

See Also: class CwiseBinaryOp, cwiseProduct(), cwiseInverse()

const CwiseUnaryOp<internal::scalar_sqrt_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > cwiseSqrt ( ) const

inlineinherited

Returns: an expression of the coefficient-wise square root of *this.

Example:

Vector3d v(1,2,4);

cout << v.cwiseSqrt() << endl;

Output:

   1
1.41
   2

See Also: cwisePow(), cwiseSquare()

const Scalar* data ( ) const

inlineinherited

Returns: a const pointer to the data array of this matrix

Scalar* data ( )

inlineinherited

Returns: a pointer to the data array of this matrix

EvalReturnType eval ( ) const

inlineinherited

Returns: the matrix or vector obtained by evaluating this expression.

Notice that in the case of a plain matrix or vector (not an expression) this function just returns a const reference, in order to avoid a useless copy.

const CwiseUnaryOp<internal::scalar_exp_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > exp ( ) const

inlineinherited

Returns: an expression of the coefficient-wise exponential of *this.

Example:

Array3d v(1,2,3);

cout << v.exp() << endl;

Output:

2.72
7.39
20.1

See Also: pow(), log(), sin(), cos()

void fill ( const Scalar & val )

inlineinherited

Alias for setConstant(): sets all coefficients in this expression to val.

See Also: setConstant(), Constant(), class CwiseNullaryOp

Referenced by PermutationBase< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType > >::determinant().

const Flagged< Derived, Added, Removed > flagged ( ) const

inlineinherited

Returns: an expression of *this with added and removed flags

This is mostly for internal use.

See Also: class Flagged

const WithFormat< Derived > format ( const IOFormat & fmt ) const

inlineinherited

Returns: a WithFormat proxy object allowing to print a matrix the with given format fmt.

See class IOFormat for some examples.

See Also: class IOFormat, class WithFormat

bool hasNaN ( ) const

inlineinherited

Returns: true is *this contains at least one Not A Number (NaN).

See Also: allFinite()

SegmentReturnType head ( Index n )

inlineinherited

Returns: a dynamic-size expression of the first coefficients of *this.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Parameters

n	the number of coefficients in the segment

Example:

RowVector4i v = RowVector4i::Random();
cout << "Here is the vector v:" << endl << v << endl;
cout << "Here is v.head(2):" << endl << v.head(2) << endl;
v.head(2).setZero();
cout << "Now the vector v is:" << endl << v << endl;

Output:

Here is the vector v:
 7 -2  6  6
Here is v.head(2):
 7 -2
Now the vector v is:
0 0 6 6

Note: Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size vector, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.

See Also: class Block, block(Index,Index)

ConstSegmentReturnType head ( Index n ) const

inlineinherited

This is the const version of head(Index).

FixedSegmentReturnType<N>::Type head ( Index n = N )

inlineinherited

Returns: a fixed-size expression of the first coefficients of *this.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Template Parameters

N	the number of coefficients in the segment as specified at compile-time

Parameters

n	the number of coefficients in the segment as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

RowVector4i v = RowVector4i::Random();
cout << "Here is the vector v:" << endl << v << endl;
cout << "Here is v.head(2):" << endl << v.head<2>() << endl;
v.head<2>().setZero();
cout << "Now the vector v is:" << endl << v << endl;

Output:

Here is the vector v:
 7 -2  6  6
Here is v.head(2):
 7 -2
Now the vector v is:
0 0 6 6

See Also: class Block

ConstFixedSegmentReturnType<N>::Type head ( Index n = N ) const

inlineinherited

This is the const version of head<int>().

const ImagReturnType imag ( ) const

inlineinherited

Returns: an read-only expression of the imaginary part of *this.

See Also: real()

NonConstImagReturnType imag ( )

inlineinherited

Returns: a non const expression of the imaginary part of *this.

See Also: real()

Index innerSize ( ) const

inlineinherited

Returns: the inner size.

Note: For a vector, this is just the size. For a matrix (non-vector), this is the minor dimension with respect to the storage order, i.e., the number of rows for a column-major matrix, and the number of columns for a row-major matrix.

References DenseBase< Derived >::IsRowMajor, and DenseBase< Derived >::IsVectorAtCompileTime.

const CwiseUnaryOp<internal::scalar_inverse_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > inverse ( ) const

inlineinherited

Returns: an expression of the coefficient-wise inverse of *this.

Example:

Array3d v(2,3,4);

cout << v.inverse() << endl;

Output:

  0.5
0.333
 0.25

See Also: operator/(), operator*()

bool isApprox	(	const DenseBase< OtherDerived > &	other,
		const RealScalar &	prec = `NumTraits<Scalar>::dummy_precision()`
	)		const

inherited

Returns: true if *this is approximately equal to other, within the precision determined by prec.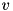

Note: The fuzzy compares are done multiplicatively. Two vectors and 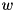are considered to be approximately equal within precision 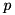if
$\Vert v - w \Vert \leqslant p\,\min(\Vert v\Vert, \Vert w\Vert).$
For matrices, the comparison is done using the Hilbert-Schmidt norm (aka Frobenius norm L2 norm).; Because of the multiplicativeness of this comparison, one can't use this function to check whether *this is approximately equal to the zero matrix or vector. Indeed, isApprox(zero) returns false unless *this itself is exactly the zero matrix or vector. If you want to test whether *this is zero, use internal::isMuchSmallerThan(const RealScalar&, RealScalar) instead.

See Also: internal::isMuchSmallerThan(const RealScalar&, RealScalar) const

Referenced by Transform< Scalar, Dim, Mode, _Options >::isApprox().

bool isApproxToConstant	(	const Scalar &	val,
		const RealScalar &	prec = `NumTraits<Scalar>::dummy_precision()`
	)		const

inherited

Returns: true if all coefficients in this matrix are approximately equal to val, to within precision prec

bool isConstant	(	const Scalar &	val,
		const RealScalar &	prec = `NumTraits<Scalar>::dummy_precision()`
	)		const

inherited

This is just an alias for isApproxToConstant().

Returns: true if all coefficients in this matrix are approximately equal to value, to within precision prec

bool isMuchSmallerThan	(	const typename NumTraits< Scalar >::Real &	other,
		const RealScalar &	prec
	)		const

inherited

Returns: true if the norm of *this is much smaller than other, within the precision determined by prec.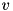

Note: The fuzzy compares are done multiplicatively. A vector is considered to be much smaller than 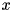within precision 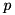if
$\Vert v \Vert \leqslant p\,\vert x\vert.$

For matrices, the comparison is done using the Hilbert-Schmidt norm. For this reason, the value of the reference scalar other should come from the Hilbert-Schmidt norm of a reference matrix of same dimensions.

See Also: isApprox(), isMuchSmallerThan(const DenseBase<OtherDerived>&, RealScalar) const

bool isMuchSmallerThan	(	const DenseBase< OtherDerived > &	other,
		const RealScalar &	prec = `NumTraits<Scalar>::dummy_precision()`
	)		const

inherited

Returns: true if the norm of *this is much smaller than the norm of other, within the precision determined by prec.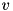

Note: The fuzzy compares are done multiplicatively. A vector is considered to be much smaller than a vector 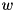within precision 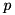if
$\Vert v \Vert \leqslant p\,\Vert w\Vert.$
For matrices, the comparison is done using the Hilbert-Schmidt norm.

See Also: isApprox(), isMuchSmallerThan(const RealScalar&, RealScalar) const

bool isOnes ( const RealScalar & prec = NumTraits<Scalar>::dummy_precision() ) const

inherited

Returns: true if *this is approximately equal to the matrix where all coefficients are equal to 1, within the precision given by prec.

Example:

Matrix3d m = Matrix3d::Ones();
m(0,2) += 1e-4;
cout << "Here's the matrix m:" << endl << m << endl;
cout << "m.isOnes() returns: " << m.isOnes() << endl;
cout << "m.isOnes(1e-3) returns: " << m.isOnes(1e-3) << endl;

Output:

Here's the matrix m:
1 1 1
1 1 1
1 1 1
m.isOnes() returns: 0
m.isOnes(1e-3) returns: 1

See Also: class CwiseNullaryOp, Ones()

bool isZero ( const RealScalar & prec = NumTraits<Scalar>::dummy_precision() ) const

inherited

Returns: true if *this is approximately equal to the zero matrix, within the precision given by prec.

Example:

Matrix3d m = Matrix3d::Zero();
m(0,2) = 1e-4;
cout << "Here's the matrix m:" << endl << m << endl;
cout << "m.isZero() returns: " << m.isZero() << endl;
cout << "m.isZero(1e-3) returns: " << m.isZero(1e-3) << endl;

Output:

Here's the matrix m:
     0      0 0.0001
     0      0      0
     0      0      0
m.isZero() returns: 0
m.isZero(1e-3) returns: 1

See Also: class CwiseNullaryOp, Zero()

Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > & lazyAssign ( const DenseBase< OtherDerived > & other )

inlineinherited

See Also: MatrixBase::lazyAssign()

ColsBlockXpr leftCols ( Index n )

inlineinherited

Returns: a block consisting of the left columns of *this.

Parameters

n	the number of columns in the block

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.leftCols(2):" << endl;
cout << a.leftCols(2) << endl;
a.leftCols(2).setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.leftCols(2):
 7  9
-2 -6
 6 -3
 6  6
Now the array a is:
 0  0 -5 -3
 0  0  1  0
 0  0  0  9
 0  0  3  9

See Also: class Block, block(Index,Index,Index,Index)

ConstColsBlockXpr leftCols ( Index n ) const

inlineinherited

This is the const version of leftCols(Index).

NColsBlockXpr<N>::Type leftCols ( Index n = N )

inlineinherited

Returns: a block consisting of the left columns of *this.

Template Parameters

N	the number of columns in the block as specified at compile-time

Parameters

n	the number of columns in the block as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.leftCols<2>():" << endl;
cout << a.leftCols<2>() << endl;
a.leftCols<2>().setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.leftCols<2>():
 7  9
-2 -6
 6 -3
 6  6
Now the array a is:
 0  0 -5 -3
 0  0  1  0
 0  0  0  9
 0  0  3  9

See Also: class Block, block(Index,Index,Index,Index)

ConstNColsBlockXpr<N>::Type leftCols ( Index n = N ) const

inlineinherited

This is the const version of leftCols<int>().

const DenseBase< Derived >::SequentialLinSpacedReturnType LinSpaced	(	Sequential_t	,
		Index	size,
		const Scalar &	low,
		const Scalar &	high
	)

inlinestaticinherited

Sets a linearly space vector.

The function generates 'size' equally spaced values in the closed interval [low,high]. This particular version of LinSpaced() uses sequential access, i.e. vector access is assumed to be a(0), a(1), ..., a(size). This assumption allows for better vectorization and yields faster code than the random access version.

When size is set to 1, a vector of length 1 containing 'high' is returned.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Example:

cout << VectorXi::LinSpaced(Sequential,4,7,10).transpose() << endl;

cout << VectorXd::LinSpaced(Sequential,5,0.0,1.0).transpose() << endl;

Output:

 7  8  9 10
   0 0.25  0.5 0.75    1

See Also: setLinSpaced(Index,const Scalar&,const Scalar&), LinSpaced(Index,Scalar,Scalar), CwiseNullaryOp

References DenseBase< Derived >::NullaryExpr().

const DenseBase< Derived >::RandomAccessLinSpacedReturnType LinSpaced	(	Index	size,
		const Scalar &	low,
		const Scalar &	high
	)

inlinestaticinherited

Sets a linearly space vector.

The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Example:

cout << VectorXi::LinSpaced(4,7,10).transpose() << endl;

cout << VectorXd::LinSpaced(5,0.0,1.0).transpose() << endl;

Output:

 7  8  9 10
   0 0.25  0.5 0.75    1

See Also: setLinSpaced(Index,const Scalar&,const Scalar&), LinSpaced(Sequential_t,Index,const Scalar&,const Scalar&,Index), CwiseNullaryOp

References DenseBase< Derived >::NullaryExpr().

const DenseBase< Derived >::SequentialLinSpacedReturnType LinSpaced	(	Sequential_t	,
		const Scalar &	low,
		const Scalar &	high
	)

inlinestaticinherited

Sets a linearly space vector.

The function generates 'size' equally spaced values in the closed interval [low,high]. This particular version of LinSpaced() uses sequential access, i.e. vector access is assumed to be a(0), a(1), ..., a(size). This assumption allows for better vectorization and yields faster code than the random access version.

When size is set to 1, a vector of length 1 containing 'high' is returned.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Example:

cout << VectorXi::LinSpaced(Sequential,4,7,10).transpose() << endl;

cout << VectorXd::LinSpaced(Sequential,5,0.0,1.0).transpose() << endl;

Output:

 7  8  9 10
   0 0.25  0.5 0.75    1

See Also: setLinSpaced(Index,const Scalar&,const Scalar&), LinSpaced(Index,Scalar,Scalar), CwiseNullaryOp Special version for fixed size types which does not require the size parameter.

References DenseBase< Derived >::NullaryExpr().

const DenseBase< Derived >::RandomAccessLinSpacedReturnType LinSpaced	(	const Scalar &	low,
		const Scalar &	high
	)

inlinestaticinherited

Sets a linearly space vector.

The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Example:

cout << VectorXi::LinSpaced(4,7,10).transpose() << endl;

cout << VectorXd::LinSpaced(5,0.0,1.0).transpose() << endl;

Output:

 7  8  9 10
   0 0.25  0.5 0.75    1

See Also: setLinSpaced(Index,const Scalar&,const Scalar&), LinSpaced(Sequential_t,Index,const Scalar&,const Scalar&,Index), CwiseNullaryOp Special version for fixed size types which does not require the size parameter.

References DenseBase< Derived >::NullaryExpr().

const CwiseUnaryOp<internal::scalar_log_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > log ( ) const

inlineinherited

Returns: an expression of the coefficient-wise logarithm of *this.

Example:

Array3d v(1,2,3);

cout << v.log() << endl;

Output:

    0
0.693
  1.1

See Also: exp()

MatrixWrapper<Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > matrix ( )

inlineinherited

Returns: an Matrix expression of this array

See Also: MatrixBase::array()

const CwiseBinaryOp< internal::scalar_max_op <Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> max ( const Eigen::ArrayBase< OtherDerived > & other ) const

inherited

Returns: an expression of the coefficient-wise max of *this and other

Example:

Array3d v(2,3,4), w(4,2,3);

cout << v.max(w) << endl;

Output:

4
3
4

See Also: min()

const CwiseBinaryOp<internal::scalar_max_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const CwiseNullaryOp<internal::scalar_constant_op<Scalar>, PlainObject> > max ( const Scalar & other ) const

inlineinherited

Returns: an expression of the coefficient-wise max of *this and scalar other

See Also: min()

internal::traits< Derived >::Scalar maxCoeff ( ) const

inlineinherited

Returns: the maximum of all coefficients of *this.

Warning: the result is undefined if *this contains NaN.

internal::traits< Derived >::Scalar maxCoeff	(	IndexType *	rowPtr,
		IndexType *	colPtr
	)		const

inherited

Returns: the maximum of all coefficients of *this and puts in *row and *col its location.

Warning: the result is undefined if *this contains NaN.

See Also: DenseBase::minCoeff(IndexType*,IndexType*), DenseBase::visitor(), DenseBase::maxCoeff()

internal::traits< Derived >::Scalar maxCoeff ( IndexType * index ) const

inherited

Returns: the maximum of all coefficients of *this and puts in *index its location.

Warning: the result is undefined if *this contains NaN.

See Also: DenseBase::maxCoeff(IndexType*,IndexType*), DenseBase::minCoeff(IndexType*,IndexType*), DenseBase::visitor(), DenseBase::maxCoeff()

internal::traits< Derived >::Scalar mean ( ) const

inlineinherited

Returns: the mean of all coefficients of *this

See Also: trace(), prod(), sum()

ColsBlockXpr middleCols	(	Index	startCol,
		Index	numCols
	)

inlineinherited

Returns: a block consisting of a range of columns of *this.

Parameters

startCol	the index of the first column in the block
numCols	the number of columns in the block

Example:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
int main(void)
{
    int const N = 5;
    MatrixXi A(N,N);
    A.setRandom();
    cout << "A =\n" << A << '\n' << endl;
    cout << "A(1..3,:) =\n" << A.middleCols(1,3) << endl;
    return 0;
}

Output:

A =
  7  -6   0   9 -10
 -2  -3   3   3  -5
  6   6  -3   5  -8
  6  -5   0  -8   6
  9   1   9   2  -7

A(1..3,:) =
-6  0  9
-3  3  3
 6 -3  5
-5  0 -8
 1  9  2

See Also: class Block, block(Index,Index,Index,Index)

ConstColsBlockXpr middleCols	(	Index	startCol,
		Index	numCols
	)		const

inlineinherited

This is the const version of middleCols(Index,Index).

NColsBlockXpr<N>::Type middleCols	(	Index	startCol,
		Index	n = `N`
	)

inlineinherited

Returns: a block consisting of a range of columns of *this.

Template Parameters

N	the number of columns in the block as specified at compile-time

Parameters

startCol	the index of the first column in the block
n	the number of columns in the block as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
int main(void)
{
    int const N = 5;
    MatrixXi A(N,N);
    A.setRandom();
    cout << "A =\n" << A << '\n' << endl;
    cout << "A(:,1..3) =\n" << A.middleCols<3>(1) << endl;
    return 0;
}

Output:

A =
  7  -6   0   9 -10
 -2  -3   3   3  -5
  6   6  -3   5  -8
  6  -5   0  -8   6
  9   1   9   2  -7

A(:,1..3) =
-6  0  9
-3  3  3
 6 -3  5
-5  0 -8
 1  9  2

See Also: class Block, block(Index,Index,Index,Index)

ConstNColsBlockXpr<N>::Type middleCols	(	Index	startCol,
		Index	n = `N`
	)		const

inlineinherited

This is the const version of middleCols<int>().

RowsBlockXpr middleRows	(	Index	startRow,
		Index	n
	)

inlineinherited

Returns: a block consisting of a range of rows of *this.

Parameters

startRow	the index of the first row in the block
n	the number of rows in the block

Example:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
int main(void)
{
    int const N = 5;
    MatrixXi A(N,N);
    A.setRandom();
    cout << "A =\n" << A << '\n' << endl;
    cout << "A(2..3,:) =\n" << A.middleRows(2,2) << endl;
    return 0;
}

Output:

A =
  7  -6   0   9 -10
 -2  -3   3   3  -5
  6   6  -3   5  -8
  6  -5   0  -8   6
  9   1   9   2  -7

A(2..3,:) =
 6  6 -3  5 -8
 6 -5  0 -8  6

See Also: class Block, block(Index,Index,Index,Index)

ConstRowsBlockXpr middleRows	(	Index	startRow,
		Index	n
	)		const

inlineinherited

This is the const version of middleRows(Index,Index).

NRowsBlockXpr<N>::Type middleRows	(	Index	startRow,
		Index	n = `N`
	)

inlineinherited

Returns: a block consisting of a range of rows of *this.

Template Parameters

N	the number of rows in the block as specified at compile-time

Parameters

startRow	the index of the first row in the block
n	the number of rows in the block as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
int main(void)
{
    int const N = 5;
    MatrixXi A(N,N);
    A.setRandom();
    cout << "A =\n" << A << '\n' << endl;
    cout << "A(1..3,:) =\n" << A.middleRows<3>(1) << endl;
    return 0;
}

Output:

A =
  7  -6   0   9 -10
 -2  -3   3   3  -5
  6   6  -3   5  -8
  6  -5   0  -8   6
  9   1   9   2  -7

A(1..3,:) =
-2 -3  3  3 -5
 6  6 -3  5 -8
 6 -5  0 -8  6

See Also: class Block, block(Index,Index,Index,Index)

ConstNRowsBlockXpr<N>::Type middleRows	(	Index	startRow,
		Index	n = `N`
	)		const

inlineinherited

This is the const version of middleRows<int>().

const CwiseBinaryOp< internal::scalar_min_op <Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> min ( const Eigen::ArrayBase< OtherDerived > & other ) const

inherited

Returns: an expression of the coefficient-wise min of *this and other

Example:

Array3d v(2,3,4), w(4,2,3);

cout << v.min(w) << endl;

Output:

2
2
3

See Also: max()

const CwiseBinaryOp<internal::scalar_min_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const CwiseNullaryOp<internal::scalar_constant_op<Scalar>, PlainObject> > min ( const Scalar & other ) const

inlineinherited

Returns: an expression of the coefficient-wise min of *this and scalar other

See Also: max()

internal::traits< Derived >::Scalar minCoeff ( ) const

inlineinherited

Returns: the minimum of all coefficients of *this.

Warning: the result is undefined if *this contains NaN.

internal::traits< Derived >::Scalar minCoeff	(	IndexType *	rowId,
		IndexType *	colId
	)		const

inherited

Returns: the minimum of all coefficients of *this and puts in *row and *col its location.

Warning: the result is undefined if *this contains NaN.

See Also: DenseBase::minCoeff(Index*), DenseBase::maxCoeff(Index*,Index*), DenseBase::visitor(), DenseBase::minCoeff()

internal::traits< Derived >::Scalar minCoeff ( IndexType * index ) const

inherited

Returns: the minimum of all coefficients of *this and puts in *index its location.

Warning: the result is undefined if *this contains NaN.

See Also: DenseBase::minCoeff(IndexType*,IndexType*), DenseBase::maxCoeff(IndexType*,IndexType*), DenseBase::visitor(), DenseBase::minCoeff()

const NestByValue< Derived > nestByValue ( ) const

inlineinherited

Returns: an expression of the temporary version of *this.

Index nonZeros ( ) const

inlineinherited

Returns: the number of nonzero coefficients which is in practice the number of stored coefficients.

const CwiseNullaryOp< CustomNullaryOp, Derived > NullaryExpr	(	Index	rows,
		Index	cols,
		const CustomNullaryOp &	func
	)

inlinestaticinherited

Returns: an expression of a matrix defined by a custom functor func

The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.

This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.

The template parameter CustomNullaryOp is the type of the functor.

See Also: class CwiseNullaryOp

Referenced by DenseBase< Derived >::Constant(), MatrixBase< Derived >::Identity(), and DenseBase< Derived >::LinSpaced().

const CwiseNullaryOp< CustomNullaryOp, Derived > NullaryExpr	(	Index	size,
		const CustomNullaryOp &	func
	)

inlinestaticinherited

Returns: an expression of a matrix defined by a custom functor func

The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.

The template parameter CustomNullaryOp is the type of the functor.

See Also: class CwiseNullaryOp

const CwiseNullaryOp< CustomNullaryOp, Derived > NullaryExpr ( const CustomNullaryOp & func )

inlinestaticinherited

Returns: an expression of a matrix defined by a custom functor func

This variant is only for fixed-size DenseBase types. For dynamic-size types, you need to use the variants taking size arguments.

The template parameter CustomNullaryOp is the type of the functor.

See Also: class CwiseNullaryOp

const DenseBase< Derived >::ConstantReturnType Ones	(	Index	nbRows,
		Index	nbCols
	)

inlinestaticinherited

Returns: an expression of a matrix where all coefficients equal one.

The parameters nbRows and nbCols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.

This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Ones() should be used instead.

Example:

cout << MatrixXi::Ones(2,3) << endl;

Output:

1 1 1
1 1 1

See Also: Ones(), Ones(Index), isOnes(), class Ones

const DenseBase< Derived >::ConstantReturnType Ones ( Index newSize )

inlinestaticinherited

Returns: an expression of a vector where all coefficients equal one.

The parameter newSize is the size of the returned vector. Must be compatible with this MatrixBase type.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Ones() should be used instead.

Example:

cout << 6 * RowVectorXi::Ones(4) << endl;

cout << VectorXf::Ones(2) << endl;

Output:

6 6 6 6
1
1

See Also: Ones(), Ones(Index,Index), isOnes(), class Ones

const DenseBase< Derived >::ConstantReturnType Ones ( )

inlinestaticinherited

Returns: an expression of a fixed-size matrix or vector where all coefficients equal one.

This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.

Example:

cout << Matrix2d::Ones() << endl;

cout << 6 * RowVector4i::Ones() << endl;

Output:

1 1
1 1
6 6 6 6

See Also: Ones(Index), Ones(Index,Index), isOnes(), class Ones

const CwiseBinaryOp<internal::scalar_boolean_and_op, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> operator&& ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient-wise && operator of *this and other

Warning: this operator is for expression of bool only.

Example:

Array3d v(-1,2,1), w(-3,2,3);

cout << ((v<w) && (v<0)) << endl;

Output:

0
0
0

See Also: operator||(), select()

const CwiseBinaryOp<internal::scalar_product_op<typename Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > ::Scalar, typename OtherDerived ::Scalar >, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived > operator* ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient wise product of *this and other

See Also: MatrixBase::cwiseProduct

const ScalarMultipleReturnType operator* ( const Scalar & scalar ) const

inlineinherited

Returns: an expression of *this scaled by the scalar factor scalar

const CwiseUnaryOp<internal::scalar_multiple2_op<Scalar,std::complex<Scalar> >, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > operator* ( const std::complex< Scalar > & scalar ) const

inlineinherited

Overloaded for efficient real matrix times complex scalar value

const CwiseBinaryOp< internal::scalar_sum_op <Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> operator+ ( const Eigen::ArrayBase< OtherDerived > & other ) const

inherited

Returns: an expression of the sum of *this and other

Note: If you want to add a given scalar to all coefficients, see Cwise::operator+().

See Also: class CwiseBinaryOp, operator+=()

const CwiseUnaryOp<internal::scalar_add_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > operator+ ( const Scalar & scalar ) const

inlineinherited

Returns: an expression of the coefficient-wise < operator of *this and other

Example:

Array3d v(1,2,3), w(3,2,1);

cout << (v<w) << endl;

Output:

1
0
0

See Also: all(), any(), operator>(), operator<=()

Returns: an expression of the coefficient-wise <= operator of *this and other

Example:

Array3d v(1,2,3), w(3,2,1);

cout << (v<=w) << endl;

Output:

1
1
0

See Also: all(), any(), operator>=(), operator<()

Returns: an expression of the coefficient-wise > operator of *this and other

Example:

Array3d v(1,2,3), w(3,2,1);

cout << (v>w) << endl;

Output:

0
0
1

See Also: all(), any(), operator>=(), operator<()

Returns: an expression of the coefficient-wise >= operator of *this and other

Example:

Array3d v(1,2,3), w(3,2,1);

cout << (v>=w) << endl;

Output:

0
1
1

See Also: all(), any(), operator>(), operator<=()

Returns: an expression of the coefficient-wise == operator of *this and other

Warning: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

Example:

Array3d v(1,2,3), w(3,2,1);

cout << (v==w) << endl;

Output:

0
1
0

See Also: all(), any(), isApprox(), isMuchSmallerThan()

Returns: an expression of the coefficient-wise != operator of *this and other

Warning: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

Example:

Array3d v(1,2,3), w(3,2,1);

cout << (v!=w) << endl;

Output:

1
0
1

See Also: all(), any(), isApprox(), isMuchSmallerThan()

Returns: an expression of *this with each coeff incremented by the constant scalar

Example:

Array3d v(1,2,3);

cout << v+5 << endl;

Output:

6
7
8

See Also: operator+=(), operator-()

const CwiseBinaryOp< internal::scalar_difference_op <Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> operator- ( const Eigen::ArrayBase< OtherDerived > & other ) const

inherited

Returns: an expression of the difference of *this and other

Note: If you want to substract a given scalar from all coefficients, see Cwise::operator-().

See Also: class CwiseBinaryOp, operator-=()

const CwiseUnaryOp<internal::scalar_opposite_op<typename internal::traits<Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > operator- ( ) const

inlineinherited

Returns: an expression of the opposite of *this

const CwiseUnaryOp<internal::scalar_add_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > operator- ( const Scalar & scalar ) const

inlineinherited

Returns: an expression of *this with each coeff decremented by the constant scalar

Example:

Array3d v(1,2,3);

cout << v-5 << endl;

Output:

-4
-3
-2

See Also: operator+(), operator-=()

const CwiseBinaryOp<internal::scalar_quotient_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> operator/ ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient wise quotient of *this and other

See Also: MatrixBase::cwiseQuotient

const CwiseUnaryOp<internal::scalar_quotient1_op<typename internal::traits<Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > operator/ ( const Scalar & scalar ) const

inlineinherited

Returns: an expression of *this divided by the scalar value scalar

CommaInitializer< Derived > operator<< ( const Scalar & s )

inlineinherited

Convenient operator to set the coefficients of a matrix.

The coefficients must be provided in a row major order and exactly match the size of the matrix. Otherwise an assertion is raised.

Example:

Matrix3i m1;
m1 << 1, 2, 3,
      4, 5, 6,
      7, 8, 9;
cout << m1 << endl << endl;
Matrix3i m2 = Matrix3i::Identity();
m2.block(0,0, 2,2) << 10, 11, 12, 13;
cout << m2 << endl << endl;
Vector2i v1;
v1 << 14, 15;
m2 << v1.transpose(), 16,
      v1, m1.block(1,1,2,2);
cout << m2 << endl;

Output:

Note: According the c++ standard, the argument expressions of this comma initializer are evaluated in arbitrary order.

See Also: CommaInitializer::finished(), class CommaInitializer

CommaInitializer< Derived > operator<< ( const DenseBase< OtherDerived > & other )

inlineinherited

See Also: operator<<(const Scalar&)

Array& operator= ( const EigenBase< OtherDerived > & other )

inline

The usage of using Base::operator=; fails on MSVC. Since the code below is working with GCC and MSVC, we skipped the usage of 'using'. This should be done only for operator=.

Array& operator= ( const ArrayBase< OtherDerived > & other )

inline

Copies the value of the expression other into *this with automatic resizing.

*this might be resized to match the dimensions of other. If *this was a null matrix (not already initialized), it will be initialized.

Note that copying a row-vector into a vector (and conversely) is allowed. The resizing, if any, is then done in the appropriate way so that row-vectors remain row-vectors and vectors remain vectors.

Array& operator= ( const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > & other )

inline

This is a special case of the templated operator=. Its purpose is to prevent a default operator= from hiding the templated operator=.

const CwiseBinaryOp<internal::scalar_boolean_or_op, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > , const OtherDerived> operator|| ( const Eigen::ArrayBase< OtherDerived > & other ) const

inlineinherited

Returns: an expression of the coefficient-wise || operator of *this and other

Warning: this operator is for expression of bool only.

Example:

Array3d v(-1,2,1), w(-3,2,3);

cout << ((v<w) || (v<0)) << endl;

Output:

1
0
1

See Also: operator&&(), select()

Index outerSize ( ) const

inlineinherited

Returns: the outer size.

Note: For a vector, this returns just 1. For a matrix (non-vector), this is the major dimension with respect to the storage order, i.e., the number of columns for a column-major matrix, and the number of rows for a row-major matrix.

References DenseBase< Derived >::IsRowMajor, and DenseBase< Derived >::IsVectorAtCompileTime.

const CwiseUnaryOp<internal::scalar_pow_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > pow ( const Scalar & exponent ) const

inlineinherited

Returns: an expression of the coefficient-wise power of *this to the given exponent.

Example:

Array3d v(8,27,64);

cout << v.pow(0.333333) << endl;

Output:

2
3
4

See Also: exp(), log()

internal::traits< Derived >::Scalar prod ( ) const

inlineinherited

Returns: the product of all coefficients of *this

Example:

Matrix3d m = Matrix3d::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the product of all the coefficients:" << endl << m.prod() << endl;

Output:

Here is the matrix m:
  0.68  0.597  -0.33
-0.211  0.823  0.536
 0.566 -0.605 -0.444
Here is the product of all the coefficients:
0.0019

See Also: sum(), mean(), trace()

References Eigen::Dynamic.

const CwiseNullaryOp< internal::scalar_random_op< typename internal::traits< Derived >::Scalar >, Derived > Random	(	Index	rows,
		Index	cols
	)

inlinestaticinherited

Returns: a random matrix expression

The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.

This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Random() should be used instead.

Example:

cout << MatrixXi::Random(2,3) << endl;

Output:

 7  6  9
-2  6 -6

This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary matrix whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.

See Also: MatrixBase::setRandom(), MatrixBase::Random(Index), MatrixBase::Random()

const CwiseNullaryOp< internal::scalar_random_op< typename internal::traits< Derived >::Scalar >, Derived > Random ( Index size )

inlinestaticinherited

Returns: a random vector expression

The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Random() should be used instead.

Example:

cout << VectorXi::Random(2) << endl;

Output:

 7
-2

This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary vector whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.

See Also: MatrixBase::setRandom(), MatrixBase::Random(Index,Index), MatrixBase::Random()

const CwiseNullaryOp< internal::scalar_random_op< typename internal::traits< Derived >::Scalar >, Derived > Random ( )

inlinestaticinherited

Returns: a fixed-size random matrix or vector expression

This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.

Example:

cout << 100 * Matrix2i::Random() << endl;

Output:

 700  600
-200  600

This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary matrix whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.

See Also: MatrixBase::setRandom(), MatrixBase::Random(Index,Index), MatrixBase::Random(Index)

RealReturnType real ( ) const

inlineinherited

Returns: a read-only expression of the real part of *this.

See Also: imag()

NonConstRealReturnType real ( )

inlineinherited

Returns: a non const expression of the real part of *this.

See Also: imag()

internal::result_of<Func(typename internal::traits<Derived>::Scalar)>::type redux ( const Func & func ) const

inlineinherited

Returns: the result of a full redux operation on the whole matrix or vector using func

The template parameter BinaryOp is the type of the functor func which must be an associative operator. Both current STL and TR1 functor styles are handled.

See Also: DenseBase::sum(), DenseBase::minCoeff(), DenseBase::maxCoeff(), MatrixBase::colwise(), MatrixBase::rowwise()

const Replicate< Derived, RowFactor, ColFactor > replicate ( ) const

inlineinherited

Returns: an expression of the replication of *this

Example:

MatrixXi m = MatrixXi::Random(2,3);
cout << "Here is the matrix m:" << endl << m << endl;
cout << "m.replicate<3,2>() = ..." << endl;
cout << m.replicate<3,2>() << endl;

Output:

Here is the matrix m:
 7  6  9
-2  6 -6
m.replicate<3,2>() = ...
 7  6  9  7  6  9
-2  6 -6 -2  6 -6
 7  6  9  7  6  9
-2  6 -6 -2  6 -6
 7  6  9  7  6  9
-2  6 -6 -2  6 -6

See Also: VectorwiseOp::replicate(), DenseBase::replicate(Index,Index), class Replicate

const DenseBase< Derived >::ReplicateReturnType replicate	(	Index	rowFactor,
		Index	colFactor
	)		const

inlineinherited

Returns: an expression of the replication of *this

Example:

Vector3i v = Vector3i::Random();
cout << "Here is the vector v:" << endl << v << endl;
cout << "v.replicate(2,5) = ..." << endl;
cout << v.replicate(2,5) << endl;

Output:

Here is the vector v:
 7
-2
 6
v.replicate(2,5) = ...
 7  7  7  7  7
-2 -2 -2 -2 -2
 6  6  6  6  6
 7  7  7  7  7
-2 -2 -2 -2 -2
 6  6  6  6  6

See Also: VectorwiseOp::replicate(), DenseBase::replicate<int,int>(), class Replicate

void resize	(	Index	nbRows,
		Index	nbCols
	)

inlineinherited

Resizes *this to a rows x cols matrix.

This method is intended for dynamic-size matrices, although it is legal to call it on any matrix as long as fixed dimensions are left unchanged. If you only want to change the number of rows and/or of columns, you can use resize(NoChange_t, Index), resize(Index, NoChange_t).

If the current number of coefficients of *this exactly matches the product rows * cols, then no memory allocation is performed and the current values are left unchanged. In all other cases, including shrinking, the data is reallocated and all previous values are lost.

Example:

MatrixXd m(2,3);
m << 1,2,3,4,5,6;
cout << "here's the 2x3 matrix m:" << endl << m << endl;
cout << "let's resize m to 3x2. This is a conservative resizing because 2*3==3*2." << endl;
m.resize(3,2);
cout << "here's the 3x2 matrix m:" << endl << m << endl;
cout << "now let's resize m to size 2x2. This is NOT a conservative resizing, so it becomes uninitialized:" << endl;
m.resize(2,2);
cout << m << endl;

Output:

here's the 2x3 matrix m:
1 2 3
4 5 6
let's resize m to 3x2. This is a conservative resizing because 2*3==3*2.
here's the 3x2 matrix m:
1 5
4 3
2 6
now let's resize m to size 2x2. This is NOT a conservative resizing, so it becomes uninitialized:
6.91e-310 2.12e-314
4.94e-324 4.94e-323

See Also: resize(Index) for vectors, resize(NoChange_t, Index), resize(Index, NoChange_t)

void resize ( Index size )

inlineinherited

Resizes *this to a vector of length size

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.. This method does not work for partially dynamic matrices when the static dimension is anything other than 1. For example it will not work with Matrix<double, 2, Dynamic>.

Example:

VectorXd v(10);
v.resize(3);
RowVector3d w;
w.resize(3); // this is legal, but has no effect
cout << "v: " << v.rows() << " rows, " << v.cols() << " cols" << endl;
cout << "w: " << w.rows() << " rows, " << w.cols() << " cols" << endl;

Output:

v: 3 rows, 1 cols
w: 1 rows, 3 cols

See Also: resize(Index,Index), resize(NoChange_t, Index), resize(Index, NoChange_t)

void resize	(	NoChange_t	,
		Index	nbCols
	)

inlineinherited

Resizes the matrix, changing only the number of columns. For the parameter of type NoChange_t, just pass the special value NoChange as in the example below.

Example:

MatrixXd m(3,4);
m.resize(NoChange, 5);
cout << "m: " << m.rows() << " rows, " << m.cols() << " cols" << endl;

Output:

m: 3 rows, 5 cols

See Also: resize(Index,Index)

void resize	(	Index	nbRows,
		NoChange_t
	)

inlineinherited

Resizes the matrix, changing only the number of rows. For the parameter of type NoChange_t, just pass the special value NoChange as in the example below.

Example:

MatrixXd m(3,4);
m.resize(5, NoChange);
cout << "m: " << m.rows() << " rows, " << m.cols() << " cols" << endl;

Output:

m: 5 rows, 4 cols

See Also: resize(Index,Index)

void resizeLike ( const EigenBase< OtherDerived > & _other )

inlineinherited

Resizes *this to have the same dimensions as other. Takes care of doing all the checking that's needed.

Note that copying a row-vector into a vector (and conversely) is allowed. The resizing, if any, is then done in the appropriate way so that row-vectors remain row-vectors and vectors remain vectors.

DenseBase< Derived >::ReverseReturnType reverse ( )

inlineinherited

Returns: an expression of the reverse of *this.

Example:

MatrixXi m = MatrixXi::Random(3,4);
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the reverse of m:" << endl << m.reverse() << endl;
cout << "Here is the coefficient (1,0) in the reverse of m:" << endl
     << m.reverse()(1,0) << endl;
cout << "Let us overwrite this coefficient with the value 4." << endl;
m.reverse()(1,0) = 4;
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  6 -3  1
-2  9  6  0
 6 -6 -5  3
Here is the reverse of m:
 3 -5 -6  6
 0  6  9 -2
 1 -3  6  7
Here is the coefficient (1,0) in the reverse of m:
0
Let us overwrite this coefficient with the value 4.
Now the matrix m is:
 7  6 -3  1
-2  9  6  4
 6 -6 -5  3

const DenseBase< Derived >::ConstReverseReturnType reverse ( ) const

inlineinherited

This is the const version of reverse().

void reverseInPlace ( )

inlineinherited

This is the "in place" version of reverse: it reverses *this.

In most cases it is probably better to simply use the reversed expression of a matrix. However, when reversing the matrix data itself is really needed, then this "in-place" version is probably the right choice because it provides the following additional features:

less error prone: doing the same operation with .reverse() requires special care:
m = m.reverse().eval();
this API allows to avoid creating a temporary (the current implementation creates a temporary, but that could be avoided using swap)
it allows future optimizations (cache friendliness, etc.)

See Also: reverse()

ColsBlockXpr rightCols ( Index n )

inlineinherited

Returns: a block consisting of the right columns of *this.

Parameters

n	the number of columns in the block

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.rightCols(2):" << endl;
cout << a.rightCols(2) << endl;
a.rightCols(2).setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.rightCols(2):
-5 -3
 1  0
 0  9
 3  9
Now the array a is:
 7  9  0  0
-2 -6  0  0
 6 -3  0  0
 6  6  0  0

See Also: class Block, block(Index,Index,Index,Index)

ConstColsBlockXpr rightCols ( Index n ) const

inlineinherited

This is the const version of rightCols(Index).

NColsBlockXpr<N>::Type rightCols ( Index n = N )

inlineinherited

Returns: a block consisting of the right columns of *this.

Template Parameters

N	the number of columns in the block as specified at compile-time

Parameters

n	the number of columns in the block as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.rightCols<2>():" << endl;
cout << a.rightCols<2>() << endl;
a.rightCols<2>().setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.rightCols<2>():
-5 -3
 1  0
 0  9
 3  9
Now the array a is:
 7  9  0  0
-2 -6  0  0
 6 -3  0  0
 6  6  0  0

See Also: class Block, block(Index,Index,Index,Index)

ConstNColsBlockXpr<N>::Type rightCols ( Index n = N ) const

inlineinherited

This is the const version of rightCols<int>().

RowXpr row ( Index i )

inlineinherited

Returns: an expression of the i-th row of *this. Note that the numbering starts at 0.

Example:

Matrix3d m = Matrix3d::Identity();
m.row(1) = Vector3d(4,5,6);
cout << m << endl;

Output:

1 0 0
4 5 6
0 0 1

See Also: col(), class Block

Referenced by VectorwiseOp< ExpressionType, Direction >::cross(), and Transform< Scalar, Dim, Mode, _Options >::pretranslate().

ConstRowXpr row ( Index i ) const

inlineinherited

This is the const version of row().

const DenseBase< Derived >::ConstRowwiseReturnType rowwise ( ) const

inlineinherited

Returns: a VectorwiseOp wrapper of *this providing additional partial reduction operations

Example:

Matrix3d m = Matrix3d::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the sum of each row:" << endl << m.rowwise().sum() << endl;
cout << "Here is the maximum absolute value of each row:"
     << endl << m.cwiseAbs().rowwise().maxCoeff() << endl;

Output:

Here is the matrix m:
  0.68  0.597  -0.33
-0.211  0.823  0.536
 0.566 -0.605 -0.444
Here is the sum of each row:
 0.948
  1.15
-0.483
Here is the maximum absolute value of each row:
 0.68
0.823
0.605

See Also: colwise(), class VectorwiseOp, Reductions, visitors and broadcasting

Referenced by Eigen::umeyama().

DenseBase< Derived >::RowwiseReturnType rowwise ( )

inlineinherited

Returns: a writable VectorwiseOp wrapper of *this providing additional partial reduction operations

See Also: colwise(), class VectorwiseOp, Reductions, visitors and broadcasting

SegmentReturnType segment	(	Index	start,
		Index	n
	)

inlineinherited

Returns: a dynamic-size expression of a segment (i.e. a vector block) in *this.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Parameters

start	the first coefficient in the segment
n	the number of coefficients in the segment

Example:

RowVector4i v = RowVector4i::Random();
cout << "Here is the vector v:" << endl << v << endl;
cout << "Here is v.segment(1, 2):" << endl << v.segment(1, 2) << endl;
v.segment(1, 2).setZero();
cout << "Now the vector v is:" << endl << v << endl;

Output:

Here is the vector v:
 7 -2  6  6
Here is v.segment(1, 2):
-2  6
Now the vector v is:
7 0 0 6

Note: Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size vector, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.

See Also: class Block, segment(Index)

ConstSegmentReturnType segment	(	Index	start,
		Index	n
	)		const

inlineinherited

This is the const version of segment(Index,Index).

FixedSegmentReturnType<N>::Type segment	(	Index	start,
		Index	n = `N`
	)

inlineinherited

Returns: a fixed-size expression of a segment (i.e. a vector block) in *this

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Template Parameters

N	the number of coefficients in the segment as specified at compile-time

Parameters

start	the index of the first element in the segment
n	the number of coefficients in the segment as specified at compile-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

RowVector4i v = RowVector4i::Random();
cout << "Here is the vector v:" << endl << v << endl;
cout << "Here is v.segment<2>(1):" << endl << v.segment<2>(1) << endl;
v.segment<2>(2).setZero();
cout << "Now the vector v is:" << endl << v << endl;

Output:

Here is the vector v:
 7 -2  6  6
Here is v.segment<2>(1):
-2  6
Now the vector v is:
 7 -2  0  0

See Also: class Block

ConstFixedSegmentReturnType<N>::Type segment	(	Index	start,
		Index	n = `N`
	)		const

inlineinherited

This is the const version of segment<int>(Index).

const Select< Derived, ThenDerived, ElseDerived > select	(	const DenseBase< ThenDerived > &	thenMatrix,
		const DenseBase< ElseDerived > &	elseMatrix
	)		const

inlineinherited

Returns: a matrix where each coefficient (i,j) is equal to thenMatrix(i,j) if *this(i,j), and elseMatrix(i,j) otherwise.

Example:

MatrixXi m(3, 3);
m << 1, 2, 3,
     4, 5, 6,
     7, 8, 9;
m = (m.array() >= 5).select(-m, m);
cout << m << endl;

Output:

 1  2  3
 4 -5 -6
-7 -8 -9

See Also: class Select

const Select< Derived, ThenDerived, typename ThenDerived::ConstantReturnType > select	(	const DenseBase< ThenDerived > &	thenMatrix,
		const typename ThenDerived::Scalar &	elseScalar
	)		const

inlineinherited

Version of DenseBase::select(const DenseBase&, const DenseBase&) with the else expression being a scalar value.

See Also: DenseBase::select(const DenseBase<ThenDerived>&, const DenseBase<ElseDerived>&) const, class Select

const Select< Derived, typename ElseDerived::ConstantReturnType, ElseDerived > select	(	const typename ElseDerived::Scalar &	thenScalar,
		const DenseBase< ElseDerived > &	elseMatrix
	)		const

inlineinherited

Version of DenseBase::select(const DenseBase&, const DenseBase&) with the then expression being a scalar value.

See Also: DenseBase::select(const DenseBase<ThenDerived>&, const DenseBase<ElseDerived>&) const, class Select

Derived & setConstant ( const Scalar & val )

inlineinherited

Sets all coefficients in this expression to value.

See Also: fill(), setConstant(Index,const Scalar&), setConstant(Index,Index,const Scalar&), setZero(), setOnes(), Constant(), class CwiseNullaryOp, setZero(), setOnes()

Derived & setLinSpaced	(	Index	newSize,
		const Scalar &	low,
		const Scalar &	high
	)

inlineinherited

Sets a linearly space vector.

The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Example:

VectorXf v;
v.setLinSpaced(5,0.5f,1.5f);
cout << v << endl;

Output:

See Also: CwiseNullaryOp

Derived & setLinSpaced	(	const Scalar &	low,
		const Scalar &	high
	)

inlineinherited

Sets a linearly space vector.

The function fill *this with equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

See Also: setLinSpaced(Index, const Scalar&, const Scalar&), CwiseNullaryOp

Derived & setOnes ( )

inlineinherited

Sets all coefficients in this expression to one.

Example:

Matrix4i m = Matrix4i::Random();
m.row(1).setOnes();
cout << m << endl;

Output:

See Also: class CwiseNullaryOp, Ones()

Derived & setRandom ( )

inlineinherited

Sets all coefficients in this expression to random values.

Example:

Matrix4i m = Matrix4i::Zero();
m.col(1).setRandom();
cout << m << endl;

Output:

See Also: class CwiseNullaryOp, setRandom(Index), setRandom(Index,Index)

Derived & setZero ( )

inlineinherited

Sets all coefficients in this expression to zero.

Example:

Matrix4i m = Matrix4i::Random();
m.row(1).setZero();
cout << m << endl;

Output:

See Also: class CwiseNullaryOp, Zero()

const CwiseUnaryOp<internal::scalar_sin_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > sin ( ) const

inlineinherited

Returns: an expression of the coefficient-wise sine of *this.

Example:

Array3d v(M_PI, M_PI/2, M_PI/3);

cout << v.sin() << endl;

Output:

1.22e-16
       1
   0.866

See Also: cos(), asin()

const CwiseUnaryOp<internal::scalar_sqrt_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > sqrt ( ) const

inlineinherited

Returns: an expression of the coefficient-wise square root of *this.

Example:

Array3d v(1,2,4);

cout << v.sqrt() << endl;

Output:

   1
1.41
   2

See Also: pow(), square()

const CwiseUnaryOp<internal::scalar_square_op<Scalar>, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > square ( ) const

inlineinherited

Returns: an expression of the coefficient-wise square of *this.

Example:

Array3d v(2,3,4);

cout << v.square() << endl;

Output:

 4
 9
16

See Also: operator/(), operator*(), abs2()

internal::traits< Derived >::Scalar sum ( ) const

inlineinherited

Returns: the sum of all coefficients of *this

See Also: trace(), prod(), mean()

References Eigen::Dynamic.

void swap ( ArrayBase< OtherDerived > const & other )

inline

Override MatrixBase::swap() since for dynamic-sized matrices of same type it is enough to swap the data pointers.

void swap	(	const DenseBase< OtherDerived > &	other,
		int	= `OtherDerived::ThisConstantIsPrivateInPlainObjectBase`
	)

inlineinherited

swaps *this with the expression other.

void swap ( PlainObjectBase< OtherDerived > & other )

inlineinherited

swaps *this with the matrix or array other.

SegmentReturnType tail ( Index n )

inlineinherited

Returns: a dynamic-size expression of the last coefficients of *this.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Parameters

n	the number of coefficients in the segment

Example:

RowVector4i v = RowVector4i::Random();
cout << "Here is the vector v:" << endl << v << endl;
cout << "Here is v.tail(2):" << endl << v.tail(2) << endl;
v.tail(2).setZero();
cout << "Now the vector v is:" << endl << v << endl;

Output:

Here is the vector v:
 7 -2  6  6
Here is v.tail(2):
6 6
Now the vector v is:
 7 -2  0  0

Note: Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size vector, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.

See Also: class Block, block(Index,Index)

ConstSegmentReturnType tail ( Index n ) const

inlineinherited

This is the const version of tail(Index).

FixedSegmentReturnType<N>::Type tail ( Index n = N )

inlineinherited

Returns: a fixed-size expression of the last coefficients of *this.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

Template Parameters

N	the number of coefficients in the segment as specified at compile-time

Parameters

n	the number of coefficients in the segment as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

RowVector4i v = RowVector4i::Random();
cout << "Here is the vector v:" << endl << v << endl;
cout << "Here is v.tail(2):" << endl << v.tail<2>() << endl;
v.tail<2>().setZero();
cout << "Now the vector v is:" << endl << v << endl;

Output:

Here is the vector v:
 7 -2  6  6
Here is v.tail(2):
6 6
Now the vector v is:
 7 -2  0  0

See Also: class Block

ConstFixedSegmentReturnType<N>::Type tail ( Index n = N ) const

inlineinherited

This is the const version of tail<int>.

const CwiseUnaryOp<internal::scalar_tan_op<Scalar>, Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > tan ( ) const

inlineinherited

Returns: an expression of the coefficient-wise tan of *this.

Example:

Array3d v(M_PI, M_PI/2, M_PI/3);

cout << v.tan() << endl;

Output:

-1.22e-16
 1.63e+16
     1.73

See Also: cos(), sin()

Block<Derived> topLeftCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: a dynamic-size expression of a top-left corner of *this.

Parameters

cRows	the number of rows in the corner
cCols	the number of columns in the corner

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.topLeftCorner(2, 2):" << endl;
cout << m.topLeftCorner(2, 2) << endl;
m.topLeftCorner(2, 2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.topLeftCorner(2, 2):
 7  9
-2 -6
Now the matrix m is:
 0  0 -5 -3
 0  0  1  0
 6 -3  0  9
 6  6  3  9

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived> topLeftCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of topLeftCorner(Index, Index).

Block<Derived, CRows, CCols> topLeftCorner ( )

inlineinherited

Returns: an expression of a fixed-size top-left corner of *this.

The template parameters CRows and CCols are the number of rows and columns in the corner.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.topLeftCorner<2,2>():" << endl;
cout << m.topLeftCorner<2,2>() << endl;
m.topLeftCorner<2,2>().setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.topLeftCorner<2,2>():
 7  9
-2 -6
Now the matrix m is:
 0  0 -5 -3
 0  0  1  0
 6 -3  0  9
 6  6  3  9

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived, CRows, CCols> topLeftCorner ( ) const

inlineinherited

This is the const version of topLeftCorner<int, int>().

Block<Derived, CRows, CCols> topLeftCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: an expression of a top-left corner of *this.

Template Parameters

CRows	number of rows in corner as specified at compile-time
CCols	number of columns in corner as specified at compile-time

Parameters

cRows	number of rows in corner as specified at run-time
cCols	number of columns in corner as specified at run-time

This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.topLeftCorner<2,Dynamic>(2,2):" << endl;
cout << m.topLeftCorner<2,Dynamic>(2,2) << endl;
m.topLeftCorner<2,Dynamic>(2,2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.topLeftCorner<2,Dynamic>(2,2):
 7  9
-2 -6
Now the matrix m is:
 0  0 -5 -3
 0  0  1  0
 6 -3  0  9
 6  6  3  9

See Also: class Block

const Block<const Derived, CRows, CCols> topLeftCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of topLeftCorner<int, int>(Index, Index).

Block<Derived> topRightCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: a dynamic-size expression of a top-right corner of *this.

Parameters

cRows	the number of rows in the corner
cCols	the number of columns in the corner

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.topRightCorner(2, 2):" << endl;
cout << m.topRightCorner(2, 2) << endl;
m.topRightCorner(2, 2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.topRightCorner(2, 2):
-5 -3
 1  0
Now the matrix m is:
 7  9  0  0
-2 -6  0  0
 6 -3  0  9
 6  6  3  9

See Also: class Block, block(Index,Index,Index,Index)

const Block<const Derived> topRightCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of topRightCorner(Index, Index).

Block<Derived, CRows, CCols> topRightCorner ( )

inlineinherited

Returns: an expression of a fixed-size top-right corner of *this.

Template Parameters

CRows	the number of rows in the corner
CCols	the number of columns in the corner

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.topRightCorner<2,2>():" << endl;
cout << m.topRightCorner<2,2>() << endl;
m.topRightCorner<2,2>().setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.topRightCorner<2,2>():
-5 -3
 1  0
Now the matrix m is:
 7  9  0  0
-2 -6  0  0
 6 -3  0  9
 6  6  3  9

See Also: class Block, block<int,int>(Index,Index)

const Block<const Derived, CRows, CCols> topRightCorner ( ) const

inlineinherited

This is the const version of topRightCorner<int, int>().

Block<Derived, CRows, CCols> topRightCorner	(	Index	cRows,
		Index	cCols
	)

inlineinherited

Returns: an expression of a top-right corner of *this.

Template Parameters

CRows	number of rows in corner as specified at compile-time
CCols	number of columns in corner as specified at compile-time

Parameters

cRows	number of rows in corner as specified at run-time
cCols	number of columns in corner as specified at run-time

This function is mainly useful for corners where the number of rows is specified at compile-time and the number of columns is specified at run-time, or vice versa. The compile-time and run-time information should not contradict. In other words, cRows should equal CRows unless CRows is Dynamic, and the same for the number of columns.

Example:

Matrix4i m = Matrix4i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is m.topRightCorner<2,Dynamic>(2,2):" << endl;
cout << m.topRightCorner<2,Dynamic>(2,2) << endl;
m.topRightCorner<2,Dynamic>(2,2).setZero();
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is m.topRightCorner<2,Dynamic>(2,2):
-5 -3
 1  0
Now the matrix m is:
 7  9  0  0
-2 -6  0  0
 6 -3  0  9
 6  6  3  9

See Also: class Block

const Block<const Derived, CRows, CCols> topRightCorner	(	Index	cRows,
		Index	cCols
	)		const

inlineinherited

This is the const version of topRightCorner<int, int>(Index, Index).

RowsBlockXpr topRows ( Index n )

inlineinherited

Returns: a block consisting of the top rows of *this.

Parameters

n	the number of rows in the block

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.topRows(2):" << endl;
cout << a.topRows(2) << endl;
a.topRows(2).setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.topRows(2):
 7  9 -5 -3
-2 -6  1  0
Now the array a is:
 0  0  0  0
 0  0  0  0
 6 -3  0  9
 6  6  3  9

See Also: class Block, block(Index,Index,Index,Index)

ConstRowsBlockXpr topRows ( Index n ) const

inlineinherited

This is the const version of topRows(Index).

NRowsBlockXpr<N>::Type topRows ( Index n = N )

inlineinherited

Returns: a block consisting of the top rows of *this.

Template Parameters

N	the number of rows in the block as specified at compile-time

Parameters

n	the number of rows in the block as specified at run-time

The compile-time and run-time information should not contradict. In other words, n should equal N unless N is Dynamic.

Example:

Array44i a = Array44i::Random();
cout << "Here is the array a:" << endl << a << endl;
cout << "Here is a.topRows<2>():" << endl;
cout << a.topRows<2>() << endl;
a.topRows<2>().setZero();
cout << "Now the array a is:" << endl << a << endl;

Output:

Here is the array a:
 7  9 -5 -3
-2 -6  1  0
 6 -3  0  9
 6  6  3  9
Here is a.topRows<2>():
 7  9 -5 -3
-2 -6  1  0
Now the array a is:
 0  0  0  0
 0  0  0  0
 6 -3  0  9
 6  6  3  9

See Also: class Block, block(Index,Index,Index,Index)

ConstNRowsBlockXpr<N>::Type topRows ( Index n = N ) const

inlineinherited

This is the const version of topRows<int>().

Transpose< Derived > transpose ( )

inlineinherited

Returns: an expression of the transpose of *this.

Example:

Matrix2i m = Matrix2i::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the transpose of m:" << endl << m.transpose() << endl;
cout << "Here is the coefficient (1,0) in the transpose of m:" << endl
     << m.transpose()(1,0) << endl;
cout << "Let us overwrite this coefficient with the value 0." << endl;
m.transpose()(1,0) = 0;
cout << "Now the matrix m is:" << endl << m << endl;

Output:

Here is the matrix m:
 7  6
-2  6
Here is the transpose of m:
 7 -2
 6  6
Here is the coefficient (1,0) in the transpose of m:
6
Let us overwrite this coefficient with the value 0.
Now the matrix m is:
 7  0
-2  6

Warning: If you want to replace a matrix by its own transpose, do NOT do this:
* m = m.transpose(); // bug!!! caused by aliasing effect

*

Instead, use the transposeInPlace() method:
* m.transposeInPlace();

*

which gives Eigen good opportunities for optimization, or alternatively you can also do:
* m = m.transpose().eval();

*

See Also: transposeInPlace(), adjoint()

Referenced by Hyperplane< _Scalar, _AmbientDim, Options >::Through().

DenseBase< Derived >::ConstTransposeReturnType transpose ( ) const

inlineinherited

This is the const version of transpose().

Make sure you read the warning for transpose() !

See Also: transposeInPlace(), adjoint()

void transposeInPlace ( )

inlineinherited

This is the "in place" version of transpose(): it replaces *this by its own transpose. Thus, doing

* m.transposeInPlace();

*

has the same effect on m as doing

* m = m.transpose().eval();

*

and is faster and also safer because in the latter line of code, forgetting the eval() results in a bug caused by aliasing.

Notice however that this method is only useful if you want to replace a matrix by its own transpose. If you just need the transpose of a matrix, use transpose().

Note: if the matrix is not square, then *this must be a resizable matrix. This excludes (non-square) fixed-size matrices, block-expressions and maps.

See Also: transpose(), adjoint(), adjointInPlace()

References Eigen::Dynamic.

const CwiseUnaryOp<CustomUnaryOp, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > unaryExpr ( const CustomUnaryOp & func = CustomUnaryOp() ) const

inlineinherited

Apply a unary operator coefficient-wise.

Parameters

[in] func Functor implementing the unary operator

Template Parameters

CustomUnaryOp Type of func

Returns: An expression of a custom coefficient-wise unary operator func of *this

The function ptr_fun() from the C++ standard library can be used to make functors out of normal functions.

Example:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
// define function to be applied coefficient-wise
double ramp(double x)
{
  if (x > 0)
    return x;
  else 
    return 0;
}
int main(int, char**)
{
  Matrix4d m1 = Matrix4d::Random();
  cout << m1 << endl << "becomes: " << endl << m1.unaryExpr(ptr_fun(ramp)) << endl;
  return 0;
}

Output:

   0.68   0.823  -0.444   -0.27
 -0.211  -0.605   0.108  0.0268
  0.566   -0.33 -0.0452   0.904
  0.597   0.536   0.258   0.832
becomes: 
  0.68  0.823      0      0
     0      0  0.108 0.0268
 0.566      0      0  0.904
 0.597  0.536  0.258  0.832

Genuine functors allow for more possibilities, for instance it may contain a state.

Example:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
// define a custom template unary functor
template<typename Scalar>
struct CwiseClampOp {
  CwiseClampOp(const Scalar& inf, const Scalar& sup) : m_inf(inf), m_sup(sup) {}
  const Scalar operator()(const Scalar& x) const { return x<m_inf ? m_inf : (x>m_sup ? m_sup : x); }
  Scalar m_inf, m_sup;
};
int main(int, char**)
{
  Matrix4d m1 = Matrix4d::Random();
  cout << m1 << endl << "becomes: " << endl << m1.unaryExpr(CwiseClampOp<double>(-0.5,0.5)) << endl;
  return 0;
}

Output:

   0.68   0.823  -0.444   -0.27
 -0.211  -0.605   0.108  0.0268
  0.566   -0.33 -0.0452   0.904
  0.597   0.536   0.258   0.832
becomes: 
    0.5     0.5  -0.444   -0.27
 -0.211    -0.5   0.108  0.0268
    0.5   -0.33 -0.0452     0.5
    0.5     0.5   0.258     0.5

See Also: class CwiseUnaryOp, class CwiseBinaryOp

const CwiseUnaryView<CustomViewOp, const Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > > unaryViewExpr ( const CustomViewOp & func = CustomViewOp() ) const

inlineinherited

Returns: an expression of a custom coefficient-wise unary operator func of *this

The template parameter CustomUnaryOp is the type of the functor of the custom unary operator.

Example:

#include <Eigen/Core>
#include <iostream>
using namespace Eigen;
using namespace std;
// define a custom template unary functor
template<typename Scalar>
struct CwiseClampOp {
  CwiseClampOp(const Scalar& inf, const Scalar& sup) : m_inf(inf), m_sup(sup) {}
  const Scalar operator()(const Scalar& x) const { return x<m_inf ? m_inf : (x>m_sup ? m_sup : x); }
  Scalar m_inf, m_sup;
};
int main(int, char**)
{
  Matrix4d m1 = Matrix4d::Random();
  cout << m1 << endl << "becomes: " << endl << m1.unaryExpr(CwiseClampOp<double>(-0.5,0.5)) << endl;
  return 0;
}

Output:

   0.68   0.823  -0.444   -0.27
 -0.211  -0.605   0.108  0.0268
  0.566   -0.33 -0.0452   0.904
  0.597   0.536   0.258   0.832
becomes: 
    0.5     0.5  -0.444   -0.27
 -0.211    -0.5   0.108  0.0268
    0.5   -0.33 -0.0452     0.5
    0.5     0.5   0.258     0.5

See Also: class CwiseUnaryOp, class CwiseBinaryOp

CoeffReturnType value ( ) const

inlineinherited

Returns: the unique coefficient of a 1x1 expression

void visit ( Visitor & visitor ) const

inherited

Applies the visitor visitor to the whole coefficients of the matrix or vector.

The template parameter Visitor is the type of the visitor and provides the following interface:

* struct MyVisitor {
*   // called for the first coefficient
*   void init(const Scalar& value, Index i, Index j);
*   // called for all other coefficients
*   void operator() (const Scalar& value, Index i, Index j);
* };
* 

Note: compared to one or two for loops, visitors offer automatic unrolling for small fixed size matrix.

See Also: minCoeff(Index*,Index*), maxCoeff(Index*,Index*), DenseBase::redux()

References Eigen::Dynamic.

const DenseBase< Derived >::ConstantReturnType Zero	(	Index	nbRows,
		Index	nbCols
	)

inlinestaticinherited

Returns: an expression of a zero matrix.

The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.

This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.

Example:

cout << MatrixXi::Zero(2,3) << endl;

Output:

0 0 0
0 0 0

See Also: Zero(), Zero(Index)

const DenseBase< Derived >::ConstantReturnType Zero ( Index size )

inlinestaticinherited

Returns: an expression of a zero vector.

The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.

This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.

This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.

Example:

cout << RowVectorXi::Zero(4) << endl;

cout << VectorXf::Zero(2) << endl;

Output:

0 0 0 0
0
0

See Also: Zero(), Zero(Index,Index)

const DenseBase< Derived >::ConstantReturnType Zero ( )

inlinestaticinherited

Returns: an expression of a fixed-size zero matrix or vector.

This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.

Example:

cout << Matrix2d::Zero() << endl;

cout << RowVector4i::Zero() << endl;

Output:

0 0
0 0
0 0 0 0

See Also: Zero(Index), Zero(Index,Index)

Friends And Related Function Documentation

std::ostream & operator<<	(	std::ostream &	s,
		const DenseBase< Derived > &	m
	)

If you wish to print the matrix with a format different than the default, use DenseBase::format().

It is also possible to change the default format by defining EIGEN_DEFAULT_IO_FORMAT before including Eigen headers. If not defined, this will automatically be defined to Eigen::IOFormat(), that is the Eigen::IOFormat with default parameters.

See Also: DenseBase::format()

The documentation for this class was generated from the following files:

Detailed Description

template<typename _Scalar, int _Rows, int _Cols, int _Options, int _MaxRows, int _MaxCols> class Eigen::Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Related Functions

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

template<typename _Scalar, int _Rows, int _Cols, int _Options, int _MaxRows, int _MaxCols>
class Eigen::Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >