Detailed Description

template<typename Scalar, int Dim, int Mode, int _Options = AutoAlign>
class Eigen::Transform< Scalar, Dim, Mode, _Options >

Represents an homogeneous transformation in a N dimensional space.

This is defined in the Geometry module.

#include <Eigen/Geometry>

Template Parameters

_Scalar	the scalar type, i.e., the type of the coefficients
_Dim	the dimension of the space
_Mode	the type of the transformation. Can be: Affine: the transformation is stored as a (Dim+1)^2 matrix, where the last row is assumed to be [0 ... 0 1]. AffineCompact: the transformation is stored as a (Dim)x(Dim+1) matrix. Projective: the transformation is stored as a (Dim+1)^2 matrix without any assumption.
_Options	has the same meaning as in class Matrix. It allows to specify DontAlign and/or RowMajor. These Options are passed directly to the underlying matrix type.

The homography is internally represented and stored by a matrix which is available through the matrix() method. To understand the behavior of this class you have to think a Transform object as its internal matrix representation. The chosen convention is right multiply:

v' = T * v

Therefore, an affine transformation matrix M is shaped like this:

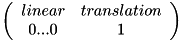
$\left( \begin{array}{cc} linear & translation\\ 0 ... 0 & 1 \end{array} \right)$

Note that for a projective transformation the last row can be anything, and then the interpretation of different parts might be sightly different.

However, unlike a plain matrix, the Transform class provides many features simplifying both its assembly and usage. In particular, it can be composed with any other transformations (Transform,Translation,RotationBase,DiagonalMatrix) and can be directly used to transform implicit homogeneous vectors. All these operations are handled via the operator*. For the composition of transformations, its principle consists to first convert the right/left hand sides of the product to a compatible (Dim+1)^2 matrix and then perform a pure matrix product. Of course, internally, operator* tries to perform the minimal number of operations according to the nature of each terms. Likewise, when applying the transform to points, the latters are automatically promoted to homogeneous vectors before doing the matrix product. The conventions to homogeneous representations are performed as follow:

Translation t (Dim)x(1): 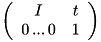$\left( \begin{array}{cc} I & t \\ 0\,...\,0 & 1 \end{array} \right)$

Rotation R (Dim)x(Dim): 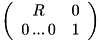$\left( \begin{array}{cc} R & 0\\ 0\,...\,0 & 1 \end{array} \right)$

Scaling DiagonalMatrix S (Dim)x(Dim): 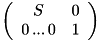$\left( \begin{array}{cc} S & 0\\ 0\,...\,0 & 1 \end{array} \right)$

Column point v (Dim)x(1): 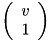$\left( \begin{array}{c} v\\ 1 \end{array} \right)$

Set of column points V1...Vn (Dim)x(n): $\left( \begin{array}{ccc} v_1 & ... & v_n\\ 1 & ... & 1 \end{array} \right)$

The concatenation of a Transform object with any kind of other transformation always returns a Transform object.

A little exception to the "as pure matrix product" rule is the case of the transformation of non homogeneous vectors by an affine transformation. In that case the last matrix row can be ignored, and the product returns non homogeneous vectors.

Since, for instance, a Dim x Dim matrix is interpreted as a linear transformation, it is not possible to directly transform Dim vectors stored in a Dim x Dim matrix. The solution is either to use a Dim x Dynamic matrix or explicitly request a vector transformation by making the vector homogeneous:

* m' = T * m.colwise().homogeneous();

*

Note that there is zero overhead.

Conversion methods from/to Qt's QMatrix and QTransform are available if the preprocessor token EIGEN_QT_SUPPORT is defined.

This class can be extended with the help of the plugin mechanism described on the page Customizing/Extending Eigen by defining the preprocessor symbol EIGEN_TRANSFORM_PLUGIN.

See Also: class Matrix, class Quaternion

Public Types
typedef internal::conditional < int(Mode)==int(AffineCompact), MatrixType &, Block < MatrixType, Dim, HDim > >::type	AffinePart

typedef internal::conditional < int(Mode)==int(AffineCompact), const MatrixType &, const Block< const MatrixType, Dim, HDim > >::type	ConstAffinePart

typedef const Block < ConstMatrixType, Dim, Dim, int(Mode)==(AffineCompact)&&(Options &RowMajor)==0 >	ConstLinearPart

typedef const MatrixType	ConstMatrixType

typedef const Block < ConstMatrixType, Dim, 1, int(Mode)==(AffineCompact)>	ConstTranslationPart

typedef Matrix< Scalar, Dim, Dim, Options >	LinearMatrixType

typedef Block< MatrixType, Dim, Dim, int(Mode)==(AffineCompact)&&(Options &RowMajor)==0 >	LinearPart

typedef internal::make_proper_matrix_type < Scalar, Rows, HDim, Options > ::type	MatrixType

typedef _Scalar	Scalar

typedef Transform< Scalar, Dim, TransformTimeDiagonalMode >	TransformTimeDiagonalReturnType

typedef Block< MatrixType, Dim, 1, int(Mode)==(AffineCompact)>	TranslationPart

typedef Translation< Scalar, Dim >	TranslationType

typedef Matrix< Scalar, Dim, 1 >	VectorType

Public Member Functions
ConstAffinePart	affine () const

AffinePart	affine ()

template<typename NewScalarType >
internal::cast_return_type < Transform, Transform < NewScalarType, Dim, Mode, Options > >::type	cast () const

template<typename RotationMatrixType , typename ScalingMatrixType >
void	computeRotationScaling (RotationMatrixType rotation, ScalingMatrixType scaling) const

template<typename ScalingMatrixType , typename RotationMatrixType >
void	computeScalingRotation (ScalingMatrixType scaling, RotationMatrixType rotation) const

const Scalar *	data () const

Scalar *	data ()

	EIGEN_MAKE_ALIGNED_OPERATOR_NEW_IF_VECTORIZABLE_FIXED_SIZE (_Scalar, _Dim==Dynamic?Dynamic:(_Dim+1)*(_Dim+1)) enum

template<typename PositionDerived , typename OrientationType , typename ScaleDerived >
Transform< Scalar, Dim, Mode, Options > &	fromPositionOrientationScale (const MatrixBase< PositionDerived > &position, const OrientationType &orientation, const MatrixBase< ScaleDerived > &scale)

Transform	inverse (TransformTraits traits=(TransformTraits) Mode) const

bool	isApprox (const Transform &other, const typename NumTraits< Scalar >::Real &prec=NumTraits< Scalar >::dummy_precision()) const

ConstLinearPart	linear () const

LinearPart	linear ()

void	makeAffine ()

const MatrixType &	matrix () const

MatrixType &	matrix ()

Scalar	operator() (Index row, Index col) const

Scalar &	operator() (Index row, Index col)

template<typename OtherDerived >
const OtherDerived::PlainObject	operator* (const EigenBase< OtherDerived > &other) const

template<typename DiagonalDerived >
const TransformTimeDiagonalReturnType	operator* (const DiagonalBase< DiagonalDerived > &b) const

const Transform	operator* (const Transform &other) const

template<int OtherMode, int OtherOptions>
internal::transform_transform_product_impl < Transform, Transform< Scalar, Dim, OtherMode, OtherOptions > >::ResultType	operator* (const Transform< Scalar, Dim, OtherMode, OtherOptions > &other) const

template<typename OtherDerived >
Transform &	operator= (const EigenBase< OtherDerived > &other)

Transform &	operator= (const QMatrix &other)

Transform &	operator= (const QTransform &other)

template<typename RotationType >
Transform< Scalar, Dim, Mode, Options > &	prerotate (const RotationType &rotation)

Transform &	prescale (const Scalar &s)

template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > &	prescale (const MatrixBase< OtherDerived > &other)

Transform &	preshear (const Scalar &sx, const Scalar &sy)

template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > &	pretranslate (const MatrixBase< OtherDerived > &other)

template<typename RotationType >
Transform< Scalar, Dim, Mode, Options > &	rotate (const RotationType &rotation)

const LinearMatrixType	rotation () const

Transform &	scale (const Scalar &s)

template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > &	scale (const MatrixBase< OtherDerived > &other)

void	setIdentity ()

Transform &	shear (const Scalar &sx, const Scalar &sy)

QMatrix	toQMatrix (void) const

QTransform	toQTransform (void) const

	Transform ()

template<typename OtherDerived >
	Transform (const EigenBase< OtherDerived > &other)

	Transform (const QMatrix &other)

	Transform (const QTransform &other)

template<typename OtherScalarType >
	Transform (const Transform< OtherScalarType, Dim, Mode, Options > &other)

template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > &	translate (const MatrixBase< OtherDerived > &other)

ConstTranslationPart	translation () const

TranslationPart	translation ()

Static Public Member Functions
static const Transform	Identity ()
	Returns an identity transformation. More...

Friends
template<typename OtherDerived >
const internal::transform_left_product_impl < OtherDerived, Mode, Options, _Dim, _Dim+1 >::ResultType	operator* (const EigenBase< OtherDerived > &a, const Transform &b)

template<typename DiagonalDerived >
TransformTimeDiagonalReturnType	operator* (const DiagonalBase< DiagonalDerived > &a, const Transform &b)

Member Typedef Documentation

typedef internal::conditional<int(Mode)==int(AffineCompact), MatrixType&, Block<MatrixType,Dim,HDim> >::type AffinePart

type of read/write reference to the affine part of the transformation

typedef internal::conditional<int(Mode)==int(AffineCompact), const MatrixType&, const Block<const MatrixType,Dim,HDim> >::type ConstAffinePart

type of read reference to the affine part of the transformation

typedef const Block<ConstMatrixType,Dim,Dim,int(Mode)==(AffineCompact) && (Options&RowMajor)==0> ConstLinearPart

type of read reference to the linear part of the transformation

typedef const MatrixType ConstMatrixType

constified MatrixType

typedef const Block<ConstMatrixType,Dim,1,int(Mode)==(AffineCompact)> ConstTranslationPart

type of a read reference to the translation part of the rotation

typedef Matrix<Scalar,Dim,Dim,Options> LinearMatrixType

type of the matrix used to represent the linear part of the transformation

typedef Block<MatrixType,Dim,Dim,int(Mode)==(AffineCompact) && (Options&RowMajor)==0> LinearPart

type of read/write reference to the linear part of the transformation

typedef internal::make_proper_matrix_type<Scalar,Rows,HDim,Options>::type MatrixType

type of the matrix used to represent the transformation

typedef _Scalar Scalar

the scalar type of the coefficients

typedef Transform<Scalar,Dim,TransformTimeDiagonalMode> TransformTimeDiagonalReturnType

The return type of the product between a diagonal matrix and a transform

typedef Block<MatrixType,Dim,1,int(Mode)==(AffineCompact)> TranslationPart

type of a read/write reference to the translation part of the rotation

typedef Translation<Scalar,Dim> TranslationType

corresponding translation type

typedef Matrix<Scalar,Dim,1> VectorType

type of a vector

Constructor & Destructor Documentation

Transform ( )

inline

Default constructor without initialization of the meaningful coefficients. If Mode==Affine, then the last row is set to [0 ... 0 1]

Transform ( const EigenBase< OtherDerived > & other )

inlineexplicit

Constructs and initializes a transformation from a Dim^2 or a (Dim+1)^2 matrix.

References EigenBase< Derived >::derived().

Transform ( const QMatrix & other )

inline

Initializes *this from a QMatrix assuming the dimension is 2.

This function is available only if the token EIGEN_QT_SUPPORT is defined.

Transform ( const QTransform< Scalar, Dim, Mode, _Options > & other )

inline

Initializes *this from a QTransform assuming the dimension is 2.

This function is available only if the token EIGEN_QT_SUPPORT is defined.

Transform ( const Transform< OtherScalarType, Dim, Mode, Options > & other )

inlineexplicit

Copy constructor with scalar type conversion

Member Function Documentation

ConstAffinePart affine ( ) const

inline

Returns: a read-only expression of the Dim x HDim affine part of the transformation

AffinePart affine ( )

inline

Returns: a writable expression of the Dim x HDim affine part of the transformation

internal::cast_return_type<Transform,Transform<NewScalarType,Dim,Mode,Options> >::type cast ( ) const

inline

Returns: *this with scalar type casted to NewScalarType

Note that if NewScalarType is equal to the current scalar type of *this then this function smartly returns a const reference to *this.

void computeRotationScaling	(	RotationMatrixType *	rotation,
		ScalingMatrixType *	scaling
	)		const

decomposes the linear part of the transformation as a product rotation x scaling, the scaling being not necessarily positive.

If either pointer is zero, the corresponding computation is skipped.

This is defined in the SVD module.

#include <Eigen/SVD>

See Also: computeScalingRotation(), rotation(), class SVD

References Eigen::ComputeFullU, Eigen::ComputeFullV, JacobiSVD< MatrixType, QRPreconditioner >::matrixU(), JacobiSVD< MatrixType, QRPreconditioner >::matrixV(), and JacobiSVD< MatrixType, QRPreconditioner >::singularValues().

void computeScalingRotation	(	ScalingMatrixType *	scaling,
		RotationMatrixType *	rotation
	)		const

decomposes the linear part of the transformation as a product rotation x scaling, the scaling being not necessarily positive.

If either pointer is zero, the corresponding computation is skipped.

This is defined in the SVD module.

#include <Eigen/SVD>

See Also: computeRotationScaling(), rotation(), class SVD

References Eigen::ComputeFullU, Eigen::ComputeFullV, JacobiSVD< MatrixType, QRPreconditioner >::matrixU(), JacobiSVD< MatrixType, QRPreconditioner >::matrixV(), and JacobiSVD< MatrixType, QRPreconditioner >::singularValues().

const Scalar* data ( ) const

inline

Returns: a const pointer to the column major internal matrix

References PlainObjectBase< Derived >::data().

Scalar* data ( )

inline

Returns: a non-const pointer to the column major internal matrix

References PlainObjectBase< Derived >::data().

EIGEN_MAKE_ALIGNED_OPERATOR_NEW_IF_VECTORIZABLE_FIXED_SIZE	(	_Scalar	,
		_Dim	= `=Dynamic ? Dynamic : (_Dim+1)*(_Dim+1)`
	)

inline

< space dimension in which the transformation holds

< size of a respective homogeneous vector

References Eigen::AffineCompact.

Transform<Scalar,Dim,Mode,Options>& fromPositionOrientationScale	(	const MatrixBase< PositionDerived > &	position,
		const OrientationType &	orientation,
		const MatrixBase< ScaleDerived > &	scale
	)

Convenient method to set *this from a position, orientation and scale of a 3D object.

References MatrixBase< Derived >::asDiagonal().

static const Transform Identity ( )

inlinestatic

Returns an identity transformation.

Transform< Scalar, Dim, Mode, Options > inverse ( TransformTraits hint = (TransformTraits)Mode ) const

inline

Returns: the inverse transformation according to some given knowledge on *this.

Parameters

hint

allows to optimize the inversion process when the transformation is known to be not a general transformation (optional). The possible values are:

Projective if the transformation is not necessarily affine, i.e., if the last row is not guaranteed to be [0 ... 0 1]
Affine if the last row can be assumed to be [0 ... 0 1]
Isometry if the transformation is only a concatenations of translations and rotations. The default is the template class parameter Mode.

Warning: unless traits is always set to NoShear or NoScaling, this function requires the generic inverse method of MatrixBase defined in the LU module. If you forget to include this module, then you will get hard to debug linking errors.

See Also: MatrixBase::inverse()

References Eigen::Affine, Eigen::Isometry, and Eigen::Projective.

bool isApprox	(	const Transform< Scalar, Dim, Mode, _Options > &	other,
		const typename NumTraits< Scalar >::Real &	prec = `NumTraits<Scalar>::dummy_precision()`
	)		const

inline

Returns: true if *this is approximately equal to other, within the precision determined by prec.

See Also: MatrixBase::isApprox()

References DenseBase< Derived >::isApprox().

ConstLinearPart linear ( ) const

inline

Returns: a read-only expression of the linear part of the transformation

Referenced by Translation< Scalar, Dim >::operator*(), Transform< Scalar, Dim, Mode, _Options >::operator*(), and Hyperplane< _Scalar, _AmbientDim, Options >::transform().

LinearPart linear ( )

inline

Returns: a writable expression of the linear part of the transformation

void makeAffine ( )

inline

Sets the last row to [0 ... 0 1]

const MatrixType& matrix ( ) const

inline

Returns: a read-only expression of the transformation matrix

Referenced by Translation< Scalar, Dim >::operator*().

MatrixType& matrix ( )

inline

Returns: a writable expression of the transformation matrix

Scalar operator()	(	Index	row,
		Index	col
	)		const

inline

shortcut for m_matrix(row,col);

See Also: MatrixBase::operator(Index,Index) const

Scalar& operator()	(	Index	row,
		Index	col
	)

inline

shortcut for m_matrix(row,col);

See Also: MatrixBase::operator(Index,Index)

const OtherDerived::PlainObject operator* ( const EigenBase< OtherDerived > & other ) const

inline

Returns: an expression of the product between the transform *this and a matrix expression other.

The right-hand-side other can be either:

an homogeneous vector of size Dim+1,
a set of homogeneous vectors of size Dim+1 x N,
a transformation matrix of size Dim+1 x Dim+1.

Moreover, if *this represents an affine transformation (i.e., Mode!=Projective), then other can also be:

a point of size Dim (computes:
this->linear() * other + this->translation()

),
a set of N points as a Dim x N matrix (computes:
(this->linear() * other).colwise() + this->translation()

),

In all cases, the return type is a matrix or vector of same sizes as the right-hand-side other.

If you want to interpret other as a linear or affine transformation, then first convert it to a Transform<> type, or do your own cooking.

Finally, if you want to apply Affine transformations to vectors, then explicitly apply the linear part only:

* Affine3f A;
* Vector3f v1, v2;
* v2 = A.linear() * v1;
* 

References EigenBase< Derived >::derived().

const TransformTimeDiagonalReturnType operator* ( const DiagonalBase< DiagonalDerived > & b ) const

inline

Returns: The product expression of a transform a times a diagonal matrix b

The rhs diagonal matrix is interpreted as an affine scaling transformation. The product results in a Transform of the same type (mode) as the lhs only if the lhs mode is no isometry. In that case, the returned transform is an affinity.

References Transform< Scalar, Dim, Mode, _Options >::linear().

const Transform operator* ( const Transform< Scalar, Dim, Mode, _Options > & other ) const

inline

Concatenates two transformations

internal::transform_transform_product_impl<Transform,Transform<Scalar,Dim,OtherMode,OtherOptions> >::ResultType operator* ( const Transform< Scalar, Dim, OtherMode, OtherOptions > & other ) const

inline

Concatenates two different transformations

Transform& operator= ( const EigenBase< OtherDerived > & other )

inline

Set *this from a Dim^2 or (Dim+1)^2 matrix.

References EigenBase< Derived >::derived().

Transform< Scalar, Dim, Mode, Options > & operator= ( const QMatrix & other )

inline

Set *this from a QMatrix assuming the dimension is 2.

This function is available only if the token EIGEN_QT_SUPPORT is defined.

Transform< Scalar, Dim, Mode, Options > & operator= ( const QTransform< Scalar, Dim, Mode, _Options > & other )

inline

Set *this from a QTransform assuming the dimension is 2.

This function is available only if the token EIGEN_QT_SUPPORT is defined.

References Eigen::AffineCompact.

Transform<Scalar,Dim,Mode,Options>& prerotate ( const RotationType & rotation )

Applies on the left the rotation represented by the rotation rotation to *this and returns a reference to *this.

See rotate() for further details.

See Also: rotate()

Transform< Scalar, Dim, Mode, Options > & prescale ( const Scalar & s )

inline

Applies on the left a uniform scale of a factor c to *this and returns a reference to *this.

See Also: scale(Scalar)

References Eigen::Isometry.

Transform<Scalar,Dim,Mode,Options>& prescale ( const MatrixBase< OtherDerived > & other )

Applies on the left the non uniform scale transformation represented by the vector other to *this and returns a reference to *this.

See Also: scale()

References MatrixBase< Derived >::asDiagonal(), and Eigen::Isometry.

Transform< Scalar, Dim, Mode, Options > & preshear	(	const Scalar &	sx,
		const Scalar &	sy
	)

Applies on the left the shear transformation represented by the vector other to *this and returns a reference to *this.

Warning: 2D only.

See Also: shear()

References Eigen::Isometry.

Transform<Scalar,Dim,Mode,Options>& pretranslate ( const MatrixBase< OtherDerived > & other )

Applies on the left the translation matrix represented by the vector other to *this and returns a reference to *this.

See Also: translate()

References Eigen::Projective, and DenseBase< Derived >::row().

Transform<Scalar,Dim,Mode,Options>& rotate ( const RotationType & rotation )

Applies on the right the rotation represented by the rotation rotation to *this and returns a reference to *this.

The template parameter RotationType is the type of the rotation which must be known by internal::toRotationMatrix<>.

Natively supported types includes:

any scalar (2D),
a Dim x Dim matrix expression,
a Quaternion (3D),
a AngleAxis (3D)

This mechanism is easily extendable to support user types such as Euler angles, or a pair of Quaternion for 4D rotations.

See Also: rotate(Scalar), class Quaternion, class AngleAxis, prerotate(RotationType)

const Transform< Scalar, Dim, Mode, Options >::LinearMatrixType rotation ( ) const

Returns: the rotation part of the transformation

This is defined in the SVD module.

#include <Eigen/SVD>

See Also: computeRotationScaling(), computeScalingRotation(), class SVD

Transform< Scalar, Dim, Mode, Options > & scale ( const Scalar & s )

inline

Applies on the right a uniform scale of a factor c to *this and returns a reference to *this.

See Also: prescale(Scalar)

References Eigen::Isometry.

Transform<Scalar,Dim,Mode,Options>& scale ( const MatrixBase< OtherDerived > & other )

Applies on the right the non uniform scale transformation represented by the vector other to *this and returns a reference to *this.

See Also: prescale()

References MatrixBase< Derived >::asDiagonal(), and Eigen::Isometry.

void setIdentity ( )

inline

See Also: MatrixBase::setIdentity()

References MatrixBase< Derived >::setIdentity().

Transform< Scalar, Dim, Mode, Options > & shear	(	const Scalar &	sx,
		const Scalar &	sy
	)

Applies on the right the shear transformation represented by the vector other to *this and returns a reference to *this.

Warning: 2D only.

See Also: preshear()

References Eigen::Isometry.

QMatrix toQMatrix ( void ) const

inline

Returns: a QMatrix from *this assuming the dimension is 2.

Warning: this conversion might loss data if *this is not affine

This function is available only if the token EIGEN_QT_SUPPORT is defined.

QTransform toQTransform ( void ) const

inline

Returns: a QTransform from *this assuming the dimension is 2.

This function is available only if the token EIGEN_QT_SUPPORT is defined.

References Eigen::AffineCompact.

Transform<Scalar,Dim,Mode,Options>& translate ( const MatrixBase< OtherDerived > & other )

Applies on the right the translation matrix represented by the vector other to *this and returns a reference to *this.

See Also: pretranslate()

ConstTranslationPart translation ( ) const

inline

Returns: a read-only expression of the translation vector of the transformation

Referenced by Translation< Scalar, Dim >::operator*(), and Hyperplane< _Scalar, _AmbientDim, Options >::transform().

TranslationPart translation ( )

inline

Returns: a writable expression of the translation vector of the transformation

Friends And Related Function Documentation

const internal::transform_left_product_impl<OtherDerived,Mode,Options,_Dim,_Dim+1>::ResultType operator*	(	const EigenBase< OtherDerived > &	a,
		const Transform< Scalar, Dim, Mode, _Options > &	b
	)

friend

Returns: the product expression of a transformation matrix a times a transform b

The left hand side other can be either:

a linear transformation matrix of size Dim x Dim,
an affine transformation matrix of size Dim x Dim+1,
a general transformation matrix of size Dim+1 x Dim+1.

TransformTimeDiagonalReturnType operator*	(	const DiagonalBase< DiagonalDerived > &	a,
		const Transform< Scalar, Dim, Mode, _Options > &	b
	)

friend

Returns: The product expression of a diagonal matrix a times a transform b

The lhs diagonal matrix is interpreted as an affine scaling transformation. The product results in a Transform of the same type (mode) as the lhs only if the lhs mode is no isometry. In that case, the returned transform is an affinity.

The documentation for this class was generated from the following files:

Detailed Description

template<typename Scalar, int Dim, int Mode, int _Options = AutoAlign> class Eigen::Transform< Scalar, Dim, Mode, _Options >

Public Types

Public Member Functions

Static Public Member Functions

Friends

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

template<typename Scalar, int Dim, int Mode, int _Options = AutoAlign>
class Eigen::Transform< Scalar, Dim, Mode, _Options >