Eigen  3.2.7
 All Classes Namespaces Functions Variables Typedefs Enumerations Enumerator Friends Groups Pages
List of all members | Public Member Functions
ColPivHouseholderQR< MatrixType > Class Template Reference
QR module

Detailed Description

template<typename MatrixType>
class Eigen::ColPivHouseholderQR< MatrixType >

Householder rank-revealing QR decomposition of a matrix with column-pivoting.

Parameters
MatrixTypethe type of the matrix of which we are computing the QR decomposition

This class performs a rank-revealing QR decomposition of a matrix A into matrices P, Q and R such that

\[ \mathbf{A} \, \mathbf{P} = \mathbf{Q} \, \mathbf{R} \]

by using Householder transformations. Here, P is a permutation matrix, Q a unitary matrix and R an upper triangular matrix.

This decomposition performs column pivoting in order to be rank-revealing and improve numerical stability. It is slower than HouseholderQR, and faster than FullPivHouseholderQR.

See Also
MatrixBase::colPivHouseholderQr()

Public Member Functions

MatrixType::RealScalar absDeterminant () const
 
 ColPivHouseholderQR ()
 Default Constructor. More...
 
 ColPivHouseholderQR (Index rows, Index cols)
 Default Constructor with memory preallocation. More...
 
 ColPivHouseholderQR (const MatrixType &matrix)
 Constructs a QR factorization from a given matrix. More...
 
const PermutationType & colsPermutation () const
 
ColPivHouseholderQR & compute (const MatrixType &matrix)
 
Index dimensionOfKernel () const
 
const HCoeffsType & hCoeffs () const
 
HouseholderSequenceType householderQ (void) const
 
ComputationInfo info () const
 Reports whether the QR factorization was succesful. More...
 
const internal::solve_retval
< ColPivHouseholderQR,
typename
MatrixType::IdentityReturnType > 		inverse () const
 
bool isInjective () const
 
bool isInvertible () const
 
bool isSurjective () const
 
MatrixType::RealScalar logAbsDeterminant () const
 
const MatrixType & matrixQR () const
 
const MatrixType & matrixR () const
 
RealScalar maxPivot () const
 
Index nonzeroPivots () const
 
Index rank () const
 
ColPivHouseholderQR & setThreshold (const RealScalar &threshold)
 
ColPivHouseholderQR & setThreshold (Default_t)
 
template<typename Rhs >
const internal::solve_retval
< ColPivHouseholderQR, Rhs > 		solve (const MatrixBase< Rhs > &b) const
 
RealScalar threshold () const
 

Constructor & Destructor Documentation

ColPivHouseholderQR ( )
inline

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via ColPivHouseholderQR::compute(const MatrixType&).

ColPivHouseholderQR ( Index  rows,
Index  cols 
)
inline

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See Also
ColPivHouseholderQR()
ColPivHouseholderQR ( const MatrixType &  matrix)
inline

Constructs a QR factorization from a given matrix.

This constructor computes the QR factorization of the matrix matrix by calling the method compute(). It is a short cut for:

* ColPivHouseholderQR<MatrixType> qr(matrix.rows(), matrix.cols());
* qr.compute(matrix);
*
See Also
compute()

References ColPivHouseholderQR< MatrixType >::compute().

Member Function Documentation

MatrixType::RealScalar absDeterminant ( ) const
Returns
the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.
Note
This is only for square matrices.
Warning
a determinant can be very big or small, so for matrices of large enough dimension, there is a risk of overflow/underflow. One way to work around that is to use logAbsDeterminant() instead.
See Also
logAbsDeterminant(), MatrixBase::determinant()
const PermutationType& colsPermutation ( ) const
inline
Returns
a const reference to the column permutation matrix
ColPivHouseholderQR< MatrixType > & compute ( const MatrixType &  matrix)

Performs the QR factorization of the given matrix matrix. The result of the factorization is stored into *this, and a reference to *this is returned.

See Also
class ColPivHouseholderQR, ColPivHouseholderQR(const MatrixType&)

Referenced by ColPivHouseholderQR< MatrixType >::ColPivHouseholderQR().

Index dimensionOfKernel ( ) const
inline
Returns
the dimension of the kernel of the matrix of which *this is the QR decomposition.
Note
This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

References ColPivHouseholderQR< MatrixType >::rank().

const HCoeffsType& hCoeffs ( ) const
inline
Returns
a const reference to the vector of Householder coefficients used to represent the factor Q.

For advanced uses only.

ColPivHouseholderQR< MatrixType >::HouseholderSequenceType householderQ ( void  ) const
Returns
the matrix Q as a sequence of householder transformations. You can extract the meaningful part only by using:
qr.householderQ().setLength(qr.nonzeroPivots())
ComputationInfo info ( ) const
inline

Reports whether the QR factorization was succesful.

Note
This function always returns Success. It is provided for compatibility with other factorization routines.
Returns
Success

References Eigen::Success.

const internal::solve_retval<ColPivHouseholderQR, typename MatrixType::IdentityReturnType> inverse ( ) const
inline
Returns
the inverse of the matrix of which *this is the QR decomposition.
Note
If this matrix is not invertible, the returned matrix has undefined coefficients. Use isInvertible() to first determine whether this matrix is invertible.
bool isInjective ( ) const
inline
Returns
true if the matrix of which *this is the QR decomposition represents an injective linear map, i.e. has trivial kernel; false otherwise.
Note
This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

References ColPivHouseholderQR< MatrixType >::rank().

Referenced by ColPivHouseholderQR< MatrixType >::isInvertible().

bool isInvertible ( ) const
inline
Returns
true if the matrix of which *this is the QR decomposition is invertible.
Note
This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

References ColPivHouseholderQR< MatrixType >::isInjective(), and ColPivHouseholderQR< MatrixType >::isSurjective().

bool isSurjective ( ) const
inline
Returns
true if the matrix of which *this is the QR decomposition represents a surjective linear map; false otherwise.
Note
This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

References ColPivHouseholderQR< MatrixType >::rank().

Referenced by ColPivHouseholderQR< MatrixType >::isInvertible().

MatrixType::RealScalar logAbsDeterminant ( ) const
Returns
the natural log of the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.
Note
This is only for square matrices.
This method is useful to work around the risk of overflow/underflow that's inherent to determinant computation.
See Also
absDeterminant(), MatrixBase::determinant()
const MatrixType& matrixQR ( ) const
inline
Returns
a reference to the matrix where the Householder QR decomposition is stored
const MatrixType& matrixR ( ) const
inline
Returns
a reference to the matrix where the result Householder QR is stored
Warning
The strict lower part of this matrix contains internal values. Only the upper triangular part should be referenced. To get it, use
matrixR().template triangularView<Upper>()
For rank-deficient matrices, use
* matrixR().topLeftCorner(rank(), rank()).template triangularView<Upper>()
*
RealScalar maxPivot ( ) const
inline
Returns
the absolute value of the biggest pivot, i.e. the biggest diagonal coefficient of R.
Index nonzeroPivots ( ) const
inline
Returns
the number of nonzero pivots in the QR decomposition. Here nonzero is meant in the exact sense, not in a fuzzy sense. So that notion isn't really intrinsically interesting, but it is still useful when implementing algorithms.
See Also
rank()
Index rank ( ) const
inline
Returns
the rank of the matrix of which *this is the QR decomposition.
Note
This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

References ColPivHouseholderQR< MatrixType >::threshold().

Referenced by ColPivHouseholderQR< MatrixType >::dimensionOfKernel(), ColPivHouseholderQR< MatrixType >::isInjective(), and ColPivHouseholderQR< MatrixType >::isSurjective().

ColPivHouseholderQR& setThreshold ( const RealScalar &  threshold)
inline

Allows to prescribe a threshold to be used by certain methods, such as rank(), who need to determine when pivots are to be considered nonzero. This is not used for the QR decomposition itself.

When it needs to get the threshold value, Eigen calls threshold(). By default, this uses a formula to automatically determine a reasonable threshold. Once you have called the present method setThreshold(const RealScalar&), your value is used instead.

Parameters
thresholdThe new value to use as the threshold.

A pivot will be considered nonzero if its absolute value is strictly greater than 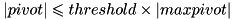$ \vert pivot \vert \leqslant threshold \times \vert maxpivot \vert $ where maxpivot is the biggest pivot.

If you want to come back to the default behavior, call setThreshold(Default_t)

References ColPivHouseholderQR< MatrixType >::threshold().

ColPivHouseholderQR& setThreshold ( Default_t  )
inline

Allows to come back to the default behavior, letting Eigen use its default formula for determining the threshold.

You should pass the special object Eigen::Default as parameter here.

qr.setThreshold(Eigen::Default);

See the documentation of setThreshold(const RealScalar&).

const internal::solve_retval<ColPivHouseholderQR, Rhs> solve ( const MatrixBase< Rhs > &  b) const
inline

This method finds a solution x to the equation Ax=b, where A is the matrix of which *this is the QR decomposition, if any exists.

Parameters
bthe right-hand-side of the equation to solve.
Returns
a solution.
Note
The case where b is a matrix is not yet implemented. Also, this code is space inefficient.

This method just tries to find as good a solution as possible. If you want to check whether a solution exists or if it is accurate, just call this function to get a result and then compute the error of this result, or use MatrixBase::isApprox() directly, for instance like this:

bool a_solution_exists = (A*result).isApprox(b, precision);

This method avoids dividing by zero, so that the non-existence of a solution doesn't by itself mean that you'll get inf or nan values.

If there exists more than one solution, this method will arbitrarily choose one.

Example:

Matrix3f m = Matrix3f::Random();
Matrix3f y = Matrix3f::Random();
cout << "Here is the matrix m:" << endl << m << endl;
cout << "Here is the matrix y:" << endl << y << endl;
Matrix3f x;
x = m.colPivHouseholderQr().solve(y);
assert(y.isApprox(m*x));
cout << "Here is a solution x to the equation mx=y:" << endl << x << endl;

Output: 

Here is the matrix m:
  0.68  0.597  -0.33
-0.211  0.823  0.536
 0.566 -0.605 -0.444
Here is the matrix y:
  0.108   -0.27   0.832
-0.0452  0.0268   0.271
  0.258   0.904   0.435
Here is a solution x to the equation mx=y:
 0.609   2.68   1.67
-0.231  -1.57 0.0713
  0.51   3.51   1.05
RealScalar threshold ( ) const
inline

Returns the threshold that will be used by certain methods such as rank().

See the documentation of setThreshold(const RealScalar&).

Referenced by ColPivHouseholderQR< MatrixType >::rank(), and ColPivHouseholderQR< MatrixType >::setThreshold().

The documentation for this class was generated from the following files: