Detailed Description

template<typename Scalar>
class Eigen::JacobiRotation< Scalar >

Rotation given by a cosine-sine pair.

This is defined in the Jacobi module.

#include <Eigen/Jacobi>

This class represents a Jacobi or Givens rotation. This is a 2D rotation in the plane J of angle 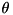$\theta$ defined by its cosine c and sine s as follow: 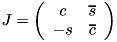$J = \left ( \begin{array}{cc} c & \overline s \\ -s & \overline c \end{array} \right )$

You can apply the respective counter-clockwise rotation to a column vector v by applying its adjoint on the left: 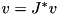$ v = J^* v $ that translates to the following Eigen code:

* v.applyOnTheLeft(J.adjoint());

*

See Also: MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight()

Public Member Functions
JacobiRotation	adjoint () const

	JacobiRotation ()

	JacobiRotation (const Scalar &c, const Scalar &s)

void	makeGivens (const Scalar &p, const Scalar &q, Scalar *z=0)

template<typename Derived >
bool	makeJacobi (const MatrixBase< Derived > &, typename Derived::Index p, typename Derived::Index q)

bool	makeJacobi (const RealScalar &x, const Scalar &y, const RealScalar &z)

JacobiRotation	operator* (const JacobiRotation &other)

JacobiRotation	transpose () const

Constructor & Destructor Documentation

JacobiRotation ( )

inline

Default constructor without any initialization.

Referenced by JacobiRotation< Scalar >::adjoint(), JacobiRotation< Scalar >::operator*(), and JacobiRotation< Scalar >::transpose().

JacobiRotation	(	const Scalar &	c,
		const Scalar &	s
	)

inline

Construct a planar rotation from a cosine-sine pair (c, s).

Member Function Documentation

JacobiRotation adjoint ( ) const

inline

Returns the adjoint transformation

References JacobiRotation< Scalar >::JacobiRotation().

void makeGivens	(	const Scalar &	p,
		const Scalar &	q,
		Scalar *	z = `0`
	)

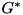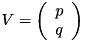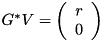Makes *this as a Givens rotation G such that applying $ G^* $ to the left of the vector $V = \left ( \begin{array}{c} p \\ q \end{array} \right )$ yields: $G^* V = \left ( \begin{array}{c} r \\ 0 \end{array} \right )$ .

The value of z is returned if z is not null (the default is null). Also note that G is built such that the cosine is always real.

Example:

Vector2f v = Vector2f::Random();
JacobiRotation<float> G;
G.makeGivens(v.x(), v.y());
cout << "Here is the vector v:" << endl << v << endl;
v.applyOnTheLeft(0, 1, G.adjoint());
cout << "Here is the vector J' * v:" << endl << v << endl;

Output:

Here is the vector v:
  0.68
-0.211
Here is the vector J' * v:
0.712
    0

This function implements the continuous Givens rotation generation algorithm found in Anderson (2000), Discontinuous Plane Rotations and the Symmetric Eigenvalue Problem. LAPACK Working Note 150, University of Tennessee, UT-CS-00-454, December 4, 2000.

See Also: MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight()

bool makeJacobi	(	const MatrixBase< Derived > &	m,
		typename Derived::Index	p,
		typename Derived::Index	q
	)

inline

Makes *this as a Jacobi rotation J such that applying J on both the right and left sides of the 2x2 selfadjoint matrix 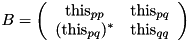$B = \left ( \begin{array}{cc} \text{this}_{pp} & \text{this}_{pq} \\ (\text{this}_{pq})^* & \text{this}_{qq} \end{array} \right )$ yields a diagonal matrix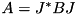 $ A = J^* B J $

Example:

Matrix2f m = Matrix2f::Random();
m = (m + m.adjoint()).eval();
JacobiRotation<float> J;
J.makeJacobi(m, 0, 1);
cout << "Here is the matrix m:" << endl << m << endl;
m.applyOnTheLeft(0, 1, J.adjoint());
m.applyOnTheRight(0, 1, J);
cout << "Here is the matrix J' * m * J:" << endl << m << endl;

Output:

Here is the matrix m:
 1.36 0.355
0.355  1.19
Here is the matrix J' * m * J:
 1.64     0
    0 0.913

See Also: JacobiRotation::makeJacobi(RealScalar, Scalar, RealScalar), MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight()

bool makeJacobi	(	const RealScalar &	x,
		const Scalar &	y,
		const RealScalar &	z
	)

Makes *this as a Jacobi rotation J such that applying J on both the right and left sides of the selfadjoint 2x2 matrix 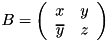$B = \left ( \begin{array}{cc} x & y \\ \overline y & z \end{array} \right )$ yields a diagonal matrix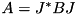 $ A = J^* B J $

See Also: MatrixBase::makeJacobi(const MatrixBase<Derived>&, Index, Index), MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight()

JacobiRotation operator* ( const JacobiRotation< Scalar > & other )

inline

Concatenates two planar rotation

References JacobiRotation< Scalar >::JacobiRotation().

JacobiRotation transpose ( ) const

inline

Returns the transposed transformation

References JacobiRotation< Scalar >::JacobiRotation().

Referenced by JacobiSVD< MatrixType, QRPreconditioner >::compute().

The documentation for this class was generated from the following files:

Detailed Description

template<typename Scalar> class Eigen::JacobiRotation< Scalar >

Public Member Functions

Constructor & Destructor Documentation

Member Function Documentation

template<typename Scalar>
class Eigen::JacobiRotation< Scalar >