 |
Eigen
3.2.7
|
 |
Eigen
3.2.7
|
A sparse direct Cholesky (LLT) factorization and solver based on the PARDISO library.
This class allows to solve for A.X = B sparse linear problems via a LL^T Cholesky factorization using the Intel MKL PARDISO library. The sparse matrix A must be selfajoint and positive definite. The vectors or matrices X and B can be either dense or sparse.
| MatrixType | the type of the sparse matrix A, it must be a SparseMatrix<> |
| UpLo | can be any bitwise combination of Upper, Lower. The default is Upper, meaning only the upper triangular part has to be used. Upper|Lower can be used to tell both triangular parts can be used as input. |
Inherits PardisoImpl< Derived >.
Public Member Functions | |
| Derived & | analyzePattern (const MatrixType &matrix) |
| Derived & | factorize (const MatrixType &matrix) |
| ComputationInfo | info () const |
| Reports whether previous computation was successful. More... | |
| ParameterType & | pardisoParameterArray () |
| template<typename Rhs > | |
| const internal::solve_retval < PardisoImpl, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| template<typename Rhs > | |
| const internal::sparse_solve_retval < PardisoImpl, Rhs > | solve (const SparseMatrixBase< Rhs > &b) const |
|
inherited |
Performs a symbolic decomposition on the sparcity of matrix.
This function is particularly useful when solving for several problems having the same structure.
|
inherited |
Performs a numeric decomposition of matrix
The given matrix must has the same sparcity than the matrix on which the symbolic decomposition has been performed.
|
inlineinherited |
Reports whether previous computation was successful.
Success if computation was succesful, NumericalIssue if the matrix appears to be negative.
|
inlineinherited |
|
inlineinherited |
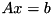 using the current decomposition of A.
using the current decomposition of A.
|
inlineinherited |
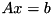 using the current decomposition of A.
using the current decomposition of A.