SPQR< MatrixType > Class Template Reference

Detailed Description

template<typename MatrixType>
class Eigen::SPQR< MatrixType >

Sparse QR factorization based on SuiteSparseQR library.

This class is used to perform a multithreaded and multifrontal rank-revealing QR decomposition of sparse matrices. The result is then used to solve linear leasts_square systems. Clearly, a QR factorization is returned such that A*P = Q*R where :

P is the column permutation. Use colsPermutation() to get it.

Q is the orthogonal matrix represented as Householder reflectors. Use matrixQ() to get an expression and matrixQ().transpose() to get the transpose. You can then apply it to a vector.

R is the sparse triangular factor. Use matrixQR() to get it as SparseMatrix. NOTE : The Index type of R is always SuiteSparse_long. You can get it with SPQR::Index

Template Parameters

_MatrixType

The type of the sparse matrix A, must be a column-major SparseMatrix<> NOTE

Public Member Functions
cholmod_common *	cholmodCommon () const
Index	cols () const
PermutationType	colsPermutation () const
	Get the permutation that was applied to columns of A.
ComputationInfo	info () const
	Reports whether previous computation was successful. More...
SPQRMatrixQReturnType< SPQR >	matrixQ () const
	Get an expression of the matrix Q.
const MatrixType	matrixR () const
Index	rank () const
Index	rows () const
void	setPivotThreshold (const RealScalar &tol)
	Set the tolerance tol to treat columns with 2-norm < =tol as zero.
void	setSPQROrdering (int ord)
	Set the fill-reducing ordering method to be used.
template<typename Rhs >
const internal::solve_retval < SPQR, Rhs >	solve (const MatrixBase< Rhs > &B) const

Member Function Documentation

cholmod_common* cholmodCommon ( ) const

inline

Returns

a pointer to the SPQR workspace

Index cols ( void  ) const

inline

Get the number of columns of the input matrix.

ComputationInfo info ( ) const

inline

Reports whether previous computation was successful.

Returns

Success if computation was succesful, NumericalIssue if the sparse QR can not be computed

const MatrixType matrixR ( ) const

inline

Returns

the sparse triangular factor R. It is a sparse matrix

Index rank ( ) const

inline

Gets the rank of the matrix. It should be equal to matrixQR().cols if the matrix is full-rank

Index rows ( void  ) const

inline

Get the number of rows of the input matrix and the Q matrix

Referenced by SPQR< MatrixType >::solve().

const internal::solve_retval<SPQR, Rhs> solve ( const MatrixBase< Rhs > &  B ) const

inline

Returns

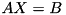the solution X of using the current decomposition of A.

See Also

compute()

References SPQR< MatrixType >::rows().

---

The documentation for this class was generated from the following file:

• SuiteSparseQRSupport.h