Functions
template<typename Index >
Index	colamd_recommended (Index nnz, Index n_row, Index n_col)
	Returns the recommended value of Alen. More...

template<typename MatrixType , typename IndexVector >
int	coletree (const MatrixType &mat, IndexVector &parent, IndexVector &firstRowElt, typename MatrixType::Index *perm=0)

template<typename LhsScalar , typename RhsScalar , int KcFactor, typename SizeType >
void	computeProductBlockingSizes (SizeType &k, SizeType &m, SizeType &n)
	Computes the blocking parameters for a m x k times k x n matrix product. More...

template<typename Index , typename IndexVector >
Index	etree_find (Index i, IndexVector &pp)

template<typename Scalar , int Flags, typename Index >
MappedSparseMatrix< Scalar, Flags, Index >	map_superlu (SluMatrix &sluMat)

template<typename Index , typename IndexVector >
void	nr_etdfs (Index n, IndexVector &parent, IndexVector &first_kid, IndexVector &next_kid, IndexVector &post, Index postnum)

template<typename Index , typename IndexVector >
void	treePostorder (Index n, IndexVector &parent, IndexVector &post)
	Post order a tree. More...

template<typename MatrixType , typename DiagonalType , typename SubDiagonalType >
void	tridiagonalization_inplace (MatrixType &mat, DiagonalType &diag, SubDiagonalType &subdiag, bool extractQ)
	Performs a full tridiagonalization in place. More...

Detailed Description

This is defined in the Jacobi module.

#include <Eigen/Jacobi>

Applies the clock wise 2D rotation j to the set of 2D vectors of cordinates x and y: 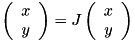$\left ( \begin{array}{cc} x \\ y \end{array} \right ) = J \left ( \begin{array}{cc} x \\ y \end{array} \right )$

See Also: MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight()

Function Documentation

Index Eigen::internal::colamd_recommended	(	Index	nnz,
		Index	n_row,
		Index	n_col
	)

inline

Returns the recommended value of Alen.

Returns recommended value of Alen for use by colamd. Returns -1 if any input argument is negative. The use of this routine or macro is optional. Note that the macro uses its arguments more than once, so be careful for side effects, if you pass expressions as arguments to COLAMD_RECOMMENDED.

Parameters

nnz	nonzeros in A
n_row	number of rows in A
n_col	number of columns in A

Returns: recommended value of Alen for use by colamd

Referenced by COLAMDOrdering< Index >::operator()().

int Eigen::internal::coletree	(	const MatrixType &	mat,
		IndexVector &	parent,
		IndexVector &	firstRowElt,
		typename MatrixType::Index *	perm = `0`
	)

Compute the column elimination tree of a sparse matrix

Parameters

mat	The matrix in column-major format.
parent	The elimination tree
firstRowElt	The column index of the first element in each row
perm	The permutation to apply to the column of mat

References etree_find().

Referenced by SparseQR< MatrixType, OrderingType >::analyzePattern(), SparseLU< _MatrixType, _OrderingType >::analyzePattern(), and SparseQR< MatrixType, OrderingType >::factorize().

void Eigen::internal::computeProductBlockingSizes	(	SizeType &	k,
		SizeType &	m,
		SizeType &	n
	)

Computes the blocking parameters for a m x k times k x n matrix product.

Parameters

[in,out]	k	Input: the third dimension of the product. Output: the blocking size along the same dimension.
[in,out]	m	Input: the number of rows of the left hand side. Output: the blocking size along the same dimension.
[in,out]	n	Input: the number of columns of the right hand side. Output: the blocking size along the same dimension.

Given a m x k times k x n matrix product of scalar types LhsScalar and RhsScalar, this function computes the blocking size parameters along the respective dimensions for matrix products and related algorithms. The blocking sizes depends on various parameters:

the L1 and L2 cache sizes,
the register level blocking sizes defined by gebp_traits,
the number of scalars that fit into a packet (when vectorization is enabled).

See Also: setCpuCacheSizes

Index Eigen::internal::etree_find	(	Index	i,
		IndexVector &	pp
	)

Find the root of the tree/set containing the vertex i : Use Path halving

Referenced by coletree().

MappedSparseMatrix<Scalar,Flags,Index> Eigen::internal::map_superlu ( SluMatrix & sluMat )

View a Super LU matrix as an Eigen expression

References Eigen::ColMajor, and Eigen::RowMajor.

void Eigen::internal::nr_etdfs	(	Index	n,
		IndexVector &	parent,
		IndexVector &	first_kid,
		IndexVector &	next_kid,
		IndexVector &	post,
		Index	postnum
	)

Depth-first search from vertex n. No recursion. This routine was contributed by Cédric Doucet, CEDRAT Group, Meylan, France.

Referenced by treePostorder().

void Eigen::internal::treePostorder	(	Index	n,
		IndexVector &	parent,
		IndexVector &	post
	)

Post order a tree.

Parameters

n	the number of nodes
parent	Input tree
post	postordered tree

References nr_etdfs().

Referenced by SparseLU< _MatrixType, _OrderingType >::analyzePattern().

void Eigen::internal::tridiagonalization_inplace	(	MatrixType &	mat,
		DiagonalType &	diag,
		SubDiagonalType &	subdiag,
		bool	extractQ
	)

Performs a full tridiagonalization in place.

Parameters

[in,out]	mat	On input, the selfadjoint matrix whose tridiagonal decomposition is to be computed. Only the lower triangular part referenced. The rest is left unchanged. On output, the orthogonal matrix Q in the decomposition if `extractQ` is true.
[out]	diag	The diagonal of the tridiagonal matrix T in the decomposition.
[out]	subdiag	The subdiagonal of the tridiagonal matrix T in the decomposition.
[in]	extractQ	If true, the orthogonal matrix Q in the decomposition is computed and stored in `mat`.

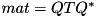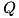Computes the tridiagonal decomposition of the selfadjoint matrix mat in place such that $ mat = Q T Q^* $ where $ Q $ is unitary and 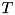$ T $ a real symmetric tridiagonal matrix.

The tridiagonal matrix T is passed to the output parameters diag and subdiag. If extractQ is true, then the orthogonal matrix Q is passed to mat. Otherwise the lower part of the matrix mat is destroyed.

The vectors diag and subdiag are not resized. The function assumes that they are already of the correct size. The length of the vector diag should equal the number of rows in mat, and the length of the vector subdiag should be one left.

This implementation contains an optimized path for 3-by-3 matrices which is especially useful for plane fitting.

Note: Currently, it requires two temporary vectors to hold the intermediate Householder coefficients, and to reconstruct the matrix Q from the Householder reflectors.

Example (this uses the same matrix as the example in Tridiagonalization::Tridiagonalization(const MatrixType&)):

MatrixXd X = MatrixXd::Random(5,5);
MatrixXd A = X + X.transpose();
cout << "Here is a random symmetric 5x5 matrix:" << endl << A << endl << endl;
VectorXd diag(5);
VectorXd subdiag(4);
internal::tridiagonalization_inplace(A, diag, subdiag, true);
cout << "The orthogonal matrix Q is:" << endl << A << endl;
cout << "The diagonal of the tridiagonal matrix T is:" << endl << diag << endl;
cout << "The subdiagonal of the tridiagonal matrix T is:" << endl << subdiag << endl;

Output:

Here is a random symmetric 5x5 matrix:
  1.36 -0.816  0.521   1.43 -0.144
-0.816 -0.659  0.794 -0.173 -0.406
 0.521  0.794 -0.541  0.461  0.179
  1.43 -0.173  0.461  -1.43  0.822
-0.144 -0.406  0.179  0.822  -1.37

The orthogonal matrix Q is:
       1        0        0        0        0
       0   -0.471    0.127   -0.671   -0.558
       0    0.301   -0.195    0.437   -0.825
       0    0.825   0.0459   -0.563 -0.00872
       0  -0.0832   -0.971   -0.202   0.0922
The diagonal of the tridiagonal matrix T is:
 1.36
 -1.2
-1.28
-1.69
0.164
The subdiagonal of the tridiagonal matrix T is:
  1.73
-0.966
 0.214
 0.345

See Also: class Tridiagonalization

Functions

Detailed Description

Function Documentation