| Description: Show that "there
exists" with an implication is always true if there
exists a situation where the antecedent is false.
Those inexperienced with formal notations of classical logic may use
expressions combining "there exists" with implication. This
is usually
a mistake, because that combination does not mean what an inexperienced
person might think it means. For example, if there is some object that
does not meet the precondition  , then the expression , then the expression
       as a whole is always true,
no matter what as a whole is always true,
no matter what  is (
is ( could
even be false, could
even be false, 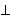 ).
New users of formal notation
who use "there exists" with an implication should consider if
they meant
"and" instead of "implies". See eximp-surprise 42530, which shows what
implication really expands to. See also empty-surprise 42528.
(Contributed by David A. Wheeler,
18-Oct-2018.) ).
New users of formal notation
who use "there exists" with an implication should consider if
they meant
"and" instead of "implies". See eximp-surprise 42530, which shows what
implication really expands to. See also empty-surprise 42528.
(Contributed by David A. Wheeler,
18-Oct-2018.) |