| Description: Demonstrate that when
using restricted "for all" over a class the
expression can be both always true and always false if the class is
empty.
Those inexperienced with formal notations of classical logic can be
surprised with what restricted "for all" does over an empty
set. It is
important to note that 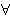 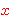 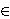   is simply an abbreviation for
  
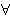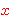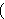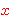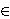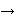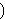(per df-ral 2917). Thus, if is the empty
set, this expression is always true regardless of the value of
(see alimp-surprise 42526).
If you want the expression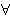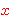
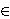to not be vacuously true,
you need to ensure that set is inhabited (e.g.,  ).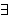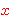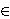
(Technical note: You can also assert that  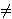 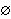; this is an
equivalent claim in classical logic as proven in n0 3931, but
in
intuitionistic logic the statement 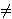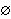is a weaker claim than
.)
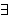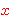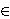Some materials on logic (particularly those that discuss
"syllogisms")
are based on the much older work by Aristotle, but Aristotle expressly
excluded empty sets from his system. Aristotle had a specific goal; he
was trying to develop a "companion-logic" for science. He
relegates
fictions like fairy godmothers and mermaids and unicorns to the realms
of poetry and literature... This is why he leaves no room for such
non-existent entities in his logic." (Groarke, "Aristotle:
Logic",
section 7. (Existential Assumptions), Internet Encyclopedia of
Philosophy, http://www.iep.utm.edu/aris-log/).
While this made
sense for his purposes, it is less flexible than modern (classical)
logic which does permit empty sets. If you wish to make claims
that
require a nonempty set, you must expressly include that requirement,
e.g., by stating 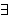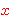. Examples of proofs
that do this include
barbari 2567, celaront 2568, and cesaro 2573.
For another "surprise" for new users of classical logic, see
alimp-surprise 42526 and eximp-surprise 42530. (Contributed by David A.
Wheeler, 20-Oct-2018.) |
![/\](wedge.gif "/\"){kind=small}
