Proof of Theorem dp15lemf
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | lea 160 |
. . . . 5
 b0 b0   a0 a0  p0 p0  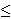 b0 b0 |
| 2 | 1 | leror 152 |
. . . 4
  b0 b0
  a0 a0  p0 p0   b2 b2 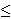  b0 b0  b2 b2 |
| 3 | 2 | lelan 167 |
. . 3
  a0 a0
 a2 a2 
  b0 b0
  a0 a0  p0 p0   b2 b2  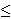   a0 a0
 a2 a2 
 b0 b0  b2 b2  |
| 4 | | leao1 162 |
. . . . . 6
 b1 b1   a0 a0  a1 a1  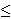  b1 b1  b2 b2 |
| 5 | 4 | mldual2i 1125 |
. . . . 5
  b1 b1
 b2 b2 
  a1 a1
 a2 a2 
 b1 b1   a0 a0  a1 a1    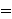    b1 b1
 b2 b2 
 a1 a1  a2 a2    b1 b1   a0 a0  a1 a1   |
| 6 | | ancom 74 |
. . . . 5
  b1 b1
 b2 b2 
  a1 a1
 a2 a2 
 b1 b1   a0 a0  a1 a1    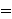    a1 a1
 a2 a2 
 b1 b1   a0 a0  a1 a1     b1 b1  b2 b2  |
| 7 | | ancom 74 |
. . . . . 6
  b1 b1
 b2 b2 
 a1 a1  a2 a2  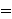   a1 a1  a2 a2   b1 b1  b2 b2  |
| 8 | 7 | ror 71 |
. . . . 5
   b1 b1  b2 b2 
 a1 a1  a2 a2    b1 b1   a0 a0  a1 a1   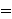    a1 a1  a2 a2   b1 b1  b2 b2    b1 b1
  a0 a0  a1 a1   |
| 9 | 5, 6, 8 | 3tr2 64 |
. . . 4
   a1 a1  a2 a2 
 b1 b1   a0 a0  a1 a1     b1 b1  b2 b2  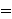    a1 a1  a2 a2   b1 b1  b2 b2    b1 b1
  a0 a0  a1 a1   |
| 10 | 9 | bile 142 |
. . 3
   a1 a1  a2 a2 
 b1 b1   a0 a0  a1 a1     b1 b1  b2 b2  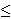    a1 a1  a2 a2   b1 b1  b2 b2    b1 b1
  a0 a0  a1 a1   |
| 11 | 3, 10 | le2or 168 |
. 2
   a0 a0  a2 a2 
  b0 b0
  a0 a0  p0 p0   b2 b2      a1 a1  a2 a2 
 b1 b1   a0 a0  a1 a1     b1 b1  b2 b2   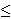    a0 a0  a2 a2   b0 b0  b2 b2      a1 a1  a2 a2   b1 b1  b2 b2    b1 b1
  a0 a0  a1 a1    |
| 12 | | or12 80 |
. 2
   a0 a0  a2 a2 
 b0 b0  b2 b2      a1 a1
 a2 a2 
 b1 b1  b2 b2    b1 b1   a0 a0  a1 a1    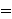    a1 a1
 a2 a2 
 b1 b1  b2 b2      a0 a0
 a2 a2 
 b0 b0  b2 b2    b1 b1   a0 a0  a1 a1    |
| 13 | 11, 12 | lbtr 139 |
1
   a0 a0  a2 a2 
  b0 b0
  a0 a0  p0 p0   b2 b2      a1 a1  a2 a2 
 b1 b1   a0 a0  a1 a1     b1 b1  b2 b2   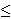    a1 a1  a2 a2   b1 b1  b2 b2      a0 a0  a2 a2   b0 b0  b2 b2    b1 b1
  a0 a0  a1 a1    |