Detailed Description

template<typename _MatrixType>
class Eigen::GeneralizedSelfAdjointEigenSolver< _MatrixType >

Computes eigenvalues and eigenvectors of the generalized selfadjoint eigen problem.

This is defined in the Eigenvalues module.

#include <Eigen/Eigenvalues>

Template Parameters

_MatrixType the type of the matrix of which we are computing the eigendecomposition; this is expected to be an instantiation of the Matrix class template.

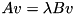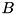This class solves the generalized eigenvalue problem $Av = \lambda Bv$ . In this case, the matrix $ A $ should be selfadjoint and the matrix $ B $ should be positive definite.

Only the lower triangular part of the input matrix is referenced.

Call the function compute() to compute the eigenvalues and eigenvectors of a given matrix. Alternatively, you can use the GeneralizedSelfAdjointEigenSolver(const MatrixType&, const MatrixType&, int) constructor which computes the eigenvalues and eigenvectors at construction time. Once the eigenvalue and eigenvectors are computed, they can be retrieved with the eigenvalues() and eigenvectors() functions.

The documentation for GeneralizedSelfAdjointEigenSolver(const MatrixType&, const MatrixType&, int) contains an example of the typical use of this class.

See Also: class SelfAdjointEigenSolver, class EigenSolver, class ComplexEigenSolver

Inheritance diagram for GeneralizedSelfAdjointEigenSolver< _MatrixType >:

Public Types
typedef NumTraits< Scalar >::Real	RealScalar
	Real scalar type for `_MatrixType`. More...

typedef internal::plain_col_type < MatrixType, RealScalar > ::type	RealVectorType
	Type for vector of eigenvalues as returned by eigenvalues(). More...

typedef MatrixType::Scalar	Scalar
	Scalar type for matrices of type `_MatrixType`.

Public Member Functions
GeneralizedSelfAdjointEigenSolver &	compute (const MatrixType &matA, const MatrixType &matB, int options=ComputeEigenvectors\|Ax_lBx)
	Computes generalized eigendecomposition of given matrix pencil. More...

SelfAdjointEigenSolver &	compute (const MatrixType &matrix, int options=ComputeEigenvectors)
	Computes eigendecomposition of given matrix. More...

SelfAdjointEigenSolver &	computeDirect (const MatrixType &matrix, int options=ComputeEigenvectors)
	Computes eigendecomposition of given matrix using a direct algorithm. More...

const RealVectorType &	eigenvalues () const
	Returns the eigenvalues of given matrix. More...

const EigenvectorsType &	eigenvectors () const
	Returns the eigenvectors of given matrix. More...

	GeneralizedSelfAdjointEigenSolver ()
	Default constructor for fixed-size matrices. More...

	GeneralizedSelfAdjointEigenSolver (Index size)
	Constructor, pre-allocates memory for dynamic-size matrices. More...

	GeneralizedSelfAdjointEigenSolver (const MatrixType &matA, const MatrixType &matB, int options=ComputeEigenvectors\|Ax_lBx)
	Constructor; computes generalized eigendecomposition of given matrix pencil. More...

ComputationInfo	info () const
	Reports whether previous computation was successful. More...

MatrixType	operatorInverseSqrt () const
	Computes the inverse square root of the matrix. More...

MatrixType	operatorSqrt () const
	Computes the positive-definite square root of the matrix. More...

Static Public Attributes
static const int	m_maxIterations
	Maximum number of iterations. More...

Member Typedef Documentation

typedef NumTraits<Scalar>::Real RealScalar

inherited

Real scalar type for _MatrixType.

This is just Scalar if Scalar is real (e.g., float or double), and the type of the real part of Scalar if Scalar is complex.

typedef internal::plain_col_type<MatrixType, RealScalar>::type RealVectorType

inherited

Type for vector of eigenvalues as returned by eigenvalues().

This is a column vector with entries of type RealScalar. The length of the vector is the size of _MatrixType.

Constructor & Destructor Documentation

GeneralizedSelfAdjointEigenSolver ( )

inline

Default constructor for fixed-size matrices.

The default constructor is useful in cases in which the user intends to perform decompositions via compute(). This constructor can only be used if _MatrixType is a fixed-size matrix; use GeneralizedSelfAdjointEigenSolver(Index) for dynamic-size matrices.

GeneralizedSelfAdjointEigenSolver ( Index size )

inline

Constructor, pre-allocates memory for dynamic-size matrices.

Parameters

[in] size Positive integer, size of the matrix whose eigenvalues and eigenvectors will be computed.

This constructor is useful for dynamic-size matrices, when the user intends to perform decompositions via compute(). The size parameter is only used as a hint. It is not an error to give a wrong size, but it may impair performance.

See Also: compute() for an example

GeneralizedSelfAdjointEigenSolver	(	const MatrixType &	matA,
		const MatrixType &	matB,
		int	options = `ComputeEigenvectors\|Ax_lBx`
	)

inline

Constructor; computes generalized eigendecomposition of given matrix pencil.

Parameters

[in]	matA	Selfadjoint matrix in matrix pencil. Only the lower triangular part of the matrix is referenced.
[in]	matB	Positive-definite matrix in matrix pencil. Only the lower triangular part of the matrix is referenced.
[in]	options	A or-ed set of flags {ComputeEigenvectors,EigenvaluesOnly} \| {Ax_lBx,ABx_lx,BAx_lx}. Default is ComputeEigenvectors\|Ax_lBx.

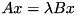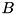This constructor calls compute(const MatrixType&, const MatrixType&, int) to compute the eigenvalues and (if requested) the eigenvectors of the generalized eigenproblem $Ax = \lambda B x$ with matA the selfadjoint matrix $ A $ and matB the positive definite matrix $ B $ . Each eigenvector 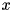$ x $ satisfies the property 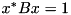$ x^* B x = 1 $ . The eigenvectors are computed if options contains ComputeEigenvectors.

In addition, the two following variants can be solved via options:

ABx_lx: 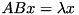$ABx = \lambda x$
BAx_lx: 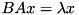$BAx = \lambda x$

Example:

MatrixXd X = MatrixXd::Random(5,5);
MatrixXd A = X + X.transpose();
cout << "Here is a random symmetric matrix, A:" << endl << A << endl;
X = MatrixXd::Random(5,5);
MatrixXd B = X * X.transpose();
cout << "and a random postive-definite matrix, B:" << endl << B << endl << endl;
GeneralizedSelfAdjointEigenSolver<MatrixXd> es(A,B);
cout << "The eigenvalues of the pencil (A,B) are:" << endl << es.eigenvalues() << endl;
cout << "The matrix of eigenvectors, V, is:" << endl << es.eigenvectors() << endl << endl;
double lambda = es.eigenvalues()[0];
cout << "Consider the first eigenvalue, lambda = " << lambda << endl;
VectorXd v = es.eigenvectors().col(0);
cout << "If v is the corresponding eigenvector, then A * v = " << endl << A * v << endl;
cout << "... and lambda * B * v = " << endl << lambda * B * v << endl << endl;

Output:

Here is a random symmetric matrix, A:
  1.36 -0.816  0.521   1.43 -0.144
-0.816 -0.659  0.794 -0.173 -0.406
 0.521  0.794 -0.541  0.461  0.179
  1.43 -0.173  0.461  -1.43  0.822
-0.144 -0.406  0.179  0.822  -1.37
and a random postive-definite matrix, B:
  0.132  0.0109 -0.0512  0.0674  -0.143
 0.0109    1.68    1.13   -1.12   0.916
-0.0512    1.13     2.3   -2.14    1.86
 0.0674   -1.12   -2.14    2.69   -2.01
 -0.143   0.916    1.86   -2.01    1.68

The eigenvalues of the pencil (A,B) are:
  -227
  -3.9
-0.837
 0.101
  54.2
The matrix of eigenvectors, V, is:
  -14.2    1.03 -0.0766  0.0273   -8.36
-0.0546   0.115  -0.729  -0.478   0.374
   9.23  -0.624  0.0165  -0.499    3.01
  -7.88    -1.3  -0.225  -0.109   -3.85
  -20.8  -0.805   0.567  0.0828   -8.73

Consider the first eigenvalue, lambda = -227
If v is the corresponding eigenvector, then A * v = 
-22.8
 28.8
-19.8
-21.9
 25.9
... and lambda * B * v = 
-22.8
 28.8
-19.8
-21.9
 25.9

See Also: compute(const MatrixType&, const MatrixType&, int)

References GeneralizedSelfAdjointEigenSolver< _MatrixType >::compute().

Member Function Documentation

GeneralizedSelfAdjointEigenSolver< MatrixType > & compute	(	const MatrixType &	matA,
		const MatrixType &	matB,
		int	options = `ComputeEigenvectors\|Ax_lBx`
	)

Computes generalized eigendecomposition of given matrix pencil.

Parameters

[in]	matA	Selfadjoint matrix in matrix pencil. Only the lower triangular part of the matrix is referenced.
[in]	matB	Positive-definite matrix in matrix pencil. Only the lower triangular part of the matrix is referenced.
[in]	options	A or-ed set of flags {ComputeEigenvectors,EigenvaluesOnly} \| {Ax_lBx,ABx_lx,BAx_lx}. Default is ComputeEigenvectors\|Ax_lBx.

Returns: Reference to *this

Accoring to options, this function computes eigenvalues and (if requested) the eigenvectors of one of the following three generalized eigenproblems:

Ax_lBx: 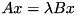$Ax = \lambda B x$
ABx_lx: 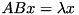$ABx = \lambda x$
BAx_lx: 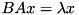$BAx = \lambda x$ with matA the selfadjoint matrix and matB the positive definite matrix 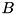. In addition, each eigenvector 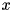satisfies the property .

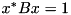The eigenvalues() function can be used to retrieve the eigenvalues. If options contains ComputeEigenvectors, then the eigenvectors are also computed and can be retrieved by calling eigenvectors().

The implementation uses LLT to compute the Cholesky decomposition 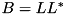$ B = LL^* $ and computes the classical eigendecomposition of the selfadjoint matrix 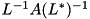$L^{-1} A (L^*)^{-1}$ if options contains Ax_lBx and of 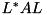$L^{*} A L$ otherwise. This solves the generalized eigenproblem, because any solution of the generalized eigenproblem 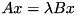$Ax = \lambda B x$ corresponds to a solution 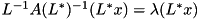$L^{-1} A (L^*)^{-1} (L^* x) = \lambda (L^* x)$ of the eigenproblem for 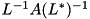$L^{-1} A (L^*)^{-1}$ . Similar statements can be made for the two other variants.

Example:

MatrixXd X = MatrixXd::Random(5,5);
MatrixXd A = X * X.transpose();
X = MatrixXd::Random(5,5);
MatrixXd B = X * X.transpose();
GeneralizedSelfAdjointEigenSolver<MatrixXd> es(A,B,EigenvaluesOnly);
cout << "The eigenvalues of the pencil (A,B) are:" << endl << es.eigenvalues() << endl;
es.compute(B,A,false);
cout << "The eigenvalues of the pencil (B,A) are:" << endl << es.eigenvalues() << endl;

Output:

The eigenvalues of the pencil (A,B) are:
  0.0289
   0.299
    2.11
    8.64
2.08e+03
The eigenvalues of the pencil (B,A) are:
0.000481
   0.116
   0.473
    3.34
    34.6

See Also: GeneralizedSelfAdjointEigenSolver(const MatrixType&, const MatrixType&, int)

References Eigen::ABx_lx, Eigen::Ax_lBx, Eigen::BAx_lx, Eigen::ComputeEigenvectors, Eigen::EigenvaluesOnly, LLT< _MatrixType, _UpLo >::matrixL(), and LLT< _MatrixType, _UpLo >::matrixU().

Referenced by GeneralizedSelfAdjointEigenSolver< _MatrixType >::GeneralizedSelfAdjointEigenSolver().

SelfAdjointEigenSolver< MatrixType > & compute	(	const MatrixType &	matrix,
		int	options = `ComputeEigenvectors`
	)

inherited

Computes eigendecomposition of given matrix.

Parameters

[in]	matrix	Selfadjoint matrix whose eigendecomposition is to be computed. Only the lower triangular part of the matrix is referenced.
[in]	options	Can be ComputeEigenvectors (default) or EigenvaluesOnly.

Returns: Reference to *this

This function computes the eigenvalues of matrix. The eigenvalues() function can be used to retrieve them. If options equals ComputeEigenvectors, then the eigenvectors are also computed and can be retrieved by calling eigenvectors().

This implementation uses a symmetric QR algorithm. The matrix is first reduced to tridiagonal form using the Tridiagonalization class. The tridiagonal matrix is then brought to diagonal form with implicit symmetric QR steps with Wilkinson shift. Details can be found in Section 8.3 of Golub & Van Loan, Matrix Computations.

The cost of the computation is about 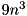$ 9n^3 $ if the eigenvectors are required and 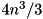$ 4n^3/3 $ if they are not required.

This method reuses the memory in the SelfAdjointEigenSolver object that was allocated when the object was constructed, if the size of the matrix does not change.

Example:

SelfAdjointEigenSolver<MatrixXf> es(4);
MatrixXf X = MatrixXf::Random(4,4);
MatrixXf A = X + X.transpose();
es.compute(A);
cout << "The eigenvalues of A are: " << es.eigenvalues().transpose() << endl;
es.compute(A + MatrixXf::Identity(4,4)); // re-use es to compute eigenvalues of A+I
cout << "The eigenvalues of A+I are: " << es.eigenvalues().transpose() << endl;

Output:

The eigenvalues of A are:  -1.58 -0.473   1.32   2.46
The eigenvalues of A+I are: -0.581  0.527   2.32   3.46

See Also: SelfAdjointEigenSolver(const MatrixType&, int)

References Eigen::ComputeEigenvectors, Eigen::NoConvergence, PlainObjectBase< Derived >::resize(), and Eigen::Success.

Referenced by SelfAdjointEigenSolver< _MatrixType >::SelfAdjointEigenSolver().

SelfAdjointEigenSolver< MatrixType > & computeDirect	(	const MatrixType &	matrix,
		int	options = `ComputeEigenvectors`
	)

inherited

Computes eigendecomposition of given matrix using a direct algorithm.

This is a variant of compute(const MatrixType&, int options) which directly solves the underlying polynomial equation.

Currently only 3x3 matrices for which the sizes are known at compile time are supported (e.g., Matrix3d).

This method is usually significantly faster than the QR algorithm but it might also be less accurate. It is also worth noting that for 3x3 matrices it involves trigonometric operations which are not necessarily available for all scalar types.

See Also: compute(const MatrixType&, int options)

const RealVectorType& eigenvalues ( ) const

inlineinherited

Returns the eigenvalues of given matrix.

Returns: A const reference to the column vector containing the eigenvalues.

Precondition: The eigenvalues have been computed before.

The eigenvalues are repeated according to their algebraic multiplicity, so there are as many eigenvalues as rows in the matrix. The eigenvalues are sorted in increasing order.

Example:

MatrixXd ones = MatrixXd::Ones(3,3);
SelfAdjointEigenSolver<MatrixXd> es(ones);
cout << "The eigenvalues of the 3x3 matrix of ones are:" 
     << endl << es.eigenvalues() << endl;

Output:

The eigenvalues of the 3x3 matrix of ones are:
-3.09e-16
        0
        3

See Also: eigenvectors(), MatrixBase::eigenvalues()

const EigenvectorsType& eigenvectors ( ) const

inlineinherited

Returns the eigenvectors of given matrix.

Returns: A const reference to the matrix whose columns are the eigenvectors.

Precondition: The eigenvectors have been computed before.

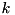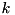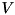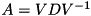Column $ k $ of the returned matrix is an eigenvector corresponding to eigenvalue number $ k $ as returned by eigenvalues(). The eigenvectors are normalized to have (Euclidean) norm equal to one. If this object was used to solve the eigenproblem for the selfadjoint matrix $ A $ , then the matrix returned by this function is the matrix $ V $ in the eigendecomposition $A = V D V^{-1}$ .

Example:

MatrixXd ones = MatrixXd::Ones(3,3);
SelfAdjointEigenSolver<MatrixXd> es(ones);
cout << "The first eigenvector of the 3x3 matrix of ones is:" 
     << endl << es.eigenvectors().col(1) << endl;

Output:

The first eigenvector of the 3x3 matrix of ones is:
     0
-0.707
 0.707

See Also: eigenvalues()

ComputationInfo info ( ) const

inlineinherited

Reports whether previous computation was successful.

Returns: Success if computation was succesful, NoConvergence otherwise.

MatrixType operatorInverseSqrt ( ) const

inlineinherited

Computes the inverse square root of the matrix.

Returns: the inverse positive-definite square root of the matrix

Precondition: The eigenvalues and eigenvectors of a positive-definite matrix have been computed before.

This function uses the eigendecomposition 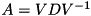$A = V D V^{-1}$ to compute the inverse square root as 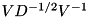$V D^{-1/2} V^{-1}$ . This is cheaper than first computing the square root with operatorSqrt() and then its inverse with MatrixBase::inverse().

Example:

MatrixXd X = MatrixXd::Random(4,4);
MatrixXd A = X * X.transpose();
cout << "Here is a random positive-definite matrix, A:" << endl << A << endl << endl;
SelfAdjointEigenSolver<MatrixXd> es(A);
cout << "The inverse square root of A is: " << endl;
cout << es.operatorInverseSqrt() << endl;
cout << "We can also compute it with operatorSqrt() and inverse(). That yields: " << endl;
cout << es.operatorSqrt().inverse() << endl;

Output:

Here is a random positive-definite matrix, A:
  1.41 -0.697 -0.111  0.508
-0.697  0.423 0.0991   -0.4
-0.111 0.0991   1.25  0.902
 0.508   -0.4  0.902    1.4

The inverse square root of A is: 
  1.88   2.78 -0.546  0.605
  2.78   8.61   -2.3   2.74
-0.546   -2.3   1.92  -1.36
 0.605   2.74  -1.36   2.18
We can also compute it with operatorSqrt() and inverse(). That yields: 
  1.88   2.78 -0.546  0.605
  2.78   8.61   -2.3   2.74
-0.546   -2.3   1.92  -1.36
 0.605   2.74  -1.36   2.18

See Also: operatorSqrt(), MatrixBase::inverse(), MatrixFunctions Module

MatrixType operatorSqrt ( ) const

inlineinherited

Computes the positive-definite square root of the matrix.

Returns: the positive-definite square root of the matrix

Precondition: The eigenvalues and eigenvectors of a positive-definite matrix have been computed before.

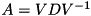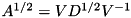The square root of a positive-definite matrix $ A $ is the positive-definite matrix whose square equals $ A $ . This function uses the eigendecomposition $A = V D V^{-1}$ to compute the square root as $A^{1/2} = V D^{1/2} V^{-1}$ .

Example:

MatrixXd X = MatrixXd::Random(4,4);
MatrixXd A = X * X.transpose();
cout << "Here is a random positive-definite matrix, A:" << endl << A << endl << endl;
SelfAdjointEigenSolver<MatrixXd> es(A);
MatrixXd sqrtA = es.operatorSqrt();
cout << "The square root of A is: " << endl << sqrtA << endl;
cout << "If we square this, we get: " << endl << sqrtA*sqrtA << endl;

Output:

Here is a random positive-definite matrix, A:
  1.41 -0.697 -0.111  0.508
-0.697  0.423 0.0991   -0.4
-0.111 0.0991   1.25  0.902
 0.508   -0.4  0.902    1.4

The square root of A is: 
   1.09  -0.432 -0.0685     0.2
 -0.432   0.379   0.141  -0.269
-0.0685   0.141       1   0.468
    0.2  -0.269   0.468    1.04
If we square this, we get: 
  1.41 -0.697 -0.111  0.508
-0.697  0.423 0.0991   -0.4
-0.111 0.0991   1.25  0.902
 0.508   -0.4  0.902    1.4

See Also: operatorInverseSqrt(), MatrixFunctions Module

Member Data Documentation

const int m_maxIterations

staticinherited

Maximum number of iterations.

The algorithm terminates if it does not converge within m_maxIterations * n iterations, where n denotes the size of the matrix. This value is currently set to 30 (copied from LAPACK).

The documentation for this class was generated from the following file:

GeneralizedSelfAdjointEigenSolver.h

Detailed Description

template<typename _MatrixType> class Eigen::GeneralizedSelfAdjointEigenSolver< _MatrixType >

Public Types

Public Member Functions

Static Public Attributes

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename _MatrixType>
class Eigen::GeneralizedSelfAdjointEigenSolver< _MatrixType >