template<typename _MatrixType, int _UpLo = Lower, typename _Ordering = AMDOrdering<typename _MatrixType::Index>>
class Eigen::SimplicialCholesky< _MatrixType, _UpLo, _Ordering >
- Deprecated:
- use SimplicialLDLT or class SimplicialLLT
- See Also
- class SimplicialLDLT, class SimplicialLLT
| void analyzePattern |
( |
const MatrixType & |
a | ) |
|
|
inline |
Performs a symbolic decomposition on the sparcity of matrix.
This function is particularly useful when solving for several problems having the same structure.
- See Also
- factorize()
Computes the sparse Cholesky decomposition of matrix
| void factorize |
( |
const MatrixType & |
a | ) |
|
|
inline |
Performs a numeric decomposition of matrix
The given matrix must has the same sparcity than the matrix on which the symbolic decomposition has been performed.
- See Also
- analyzePattern()
Reports whether previous computation was successful.
- Returns
Success if computation was succesful, NumericalIssue if the matrix.appears to be negative.
| SimplicialCholesky< _MatrixType, _UpLo, _Ordering > & setShift |
( |
const RealScalar & |
offset, |
|
|
const RealScalar & |
scale = 1 |
|
) |
| |
|
inlineinherited |
Sets the shift parameters that will be used to adjust the diagonal coefficients during the numerical factorization.
During the numerical factorization, the diagonal coefficients are transformed by the following linear model:
d_ii = offset + scale * d_ii
The default is the identity transformation with offset=0, and scale=1.
- Returns
- a reference to
*this.
- Returns
- the solution x of
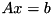 using the current decomposition of A.
using the current decomposition of A.
- See Also
- compute()
- Returns
- the solution x of
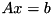 using the current decomposition of A.
using the current decomposition of A.
- See Also
- compute()
The documentation for this class was generated from the following file:


 Inheritance diagram for SimplicialCholesky< _MatrixType, _UpLo, _Ordering >:
Inheritance diagram for SimplicialCholesky< _MatrixType, _UpLo, _Ordering >: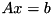 using the current decomposition of A.
using the current decomposition of A.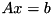 using the current decomposition of A.
using the current decomposition of A.