 |
Eigen
3.2.7
|
 |
Eigen
3.2.7
|
A direct sparse LDLT Cholesky factorizations without square root.
This class provides a LDL^T Cholesky factorizations without square root of sparse matrices that are selfadjoint and positive definite. The factorization allows for solving A.X = B where X and B can be either dense or sparse.
In order to reduce the fill-in, a symmetric permutation P is applied prior to the factorization such that the factorized matrix is P A P^-1.
| _MatrixType | the type of the sparse matrix A, it must be a SparseMatrix<> |
| _UpLo | the triangular part that will be used for the computations. It can be Lower or Upper. Default is Lower. |
| _Ordering | The ordering method to use, either AMDOrdering<> or NaturalOrdering<>. Default is AMDOrdering<> |
 Inheritance diagram for SimplicialLDLT< _MatrixType, _UpLo, _Ordering >:
Inheritance diagram for SimplicialLDLT< _MatrixType, _UpLo, _Ordering >:Public Member Functions | |
| void | analyzePattern (const MatrixType &a) |
| SimplicialLDLT & | compute (const MatrixType &matrix) |
| Scalar | determinant () const |
| void | factorize (const MatrixType &a) |
| ComputationInfo | info () const |
| Reports whether previous computation was successful. More... | |
| const MatrixL | matrixL () const |
| const MatrixU | matrixU () const |
| const PermutationMatrix < Dynamic, Dynamic, Index > & | permutationP () const |
| const PermutationMatrix < Dynamic, Dynamic, Index > & | permutationPinv () const |
| SimplicialLDLT< _MatrixType, _UpLo, _Ordering > & | setShift (const RealScalar &offset, const RealScalar &scale=1) |
| SimplicialLDLT () | |
| SimplicialLDLT (const MatrixType &matrix) | |
| const internal::solve_retval < SimplicialCholeskyBase, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| const internal::sparse_solve_retval < SimplicialCholeskyBase, Rhs > | solve (const SparseMatrixBase< Rhs > &b) const |
| const VectorType | vectorD () const |
|
inline |
Default constructor
|
inline |
Constructs and performs the LLT factorization of matrix
|
inline |
Performs a symbolic decomposition on the sparcity of matrix.
This function is particularly useful when solving for several problems having the same structure.
|
inline |
Computes the sparse Cholesky decomposition of matrix
|
inline |
|
inline |
Performs a numeric decomposition of matrix
The given matrix must has the same sparcity than the matrix on which the symbolic decomposition has been performed.
|
inlineinherited |
Reports whether previous computation was successful.
Success if computation was succesful, NumericalIssue if the matrix.appears to be negative.
|
inline |
|
inline |
|
inlineinherited |
|
inlineinherited |
|
inlineinherited |
Sets the shift parameters that will be used to adjust the diagonal coefficients during the numerical factorization.
During the numerical factorization, the diagonal coefficients are transformed by the following linear model:
d_ii = offset + scale * d_ii
The default is the identity transformation with offset=0, and scale=1.
*this.
|
inlineinherited |
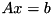 using the current decomposition of A.
using the current decomposition of A.
|
inlineinherited |
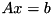 using the current decomposition of A.
using the current decomposition of A.References EigenBase< Derived >::derived(), and SparseMatrixBase< Derived >::rows().
|
inline |