5 Structured Programming in Python
5.1 Introduction
In Part I you had an intensive introduction to Python (Chapter 1) followed by chapters on words, tags, and chunks (Chapters 2-6). These chapters contain many examples and exercises that should have helped you consolidate your Python skills and apply them to simple NLP tasks. So far our programs — and the data we have been processing — have been relatively unstructured. In Part II we will focus on structure: i.e. structured programming with structured data.
In this chapter we will review key programming concepts and explain many of the minor points that could easily trip you up. More fundamentally, we will introduce important concepts in structured programming that help you write readable, well-organized programs that you and others will be able to re-use. Each section is independent, so you can easily select what you most need to learn and concentrate on that. As before, this chapter contains many examples and exercises (and as before, some exercises introduce new material). Readers new to programming should work through them carefully and consult other introductions to programming if necessary; experienced programmers can quickly skim this chapter.
Note
Remember that our program samples assume you begin your interactive session or your program with: import nltk, re, pprint
5.2 Back to the Basics
Let's begin by revisiting some of the fundamental operations and data structures required for natural language processing in Python. It is important to appreciate several finer points in order to write Python programs that are not only correct but also idiomatic — by this, we mean using the features of the Python language in a natural and concise way. To illustrate, here is a technique for iterating over the members of a list by initializing an index i and then incrementing the index each time we pass through the loop:
|
Although this does the job, it is not idiomatic Python. By contrast, Python's for statement allows us to achieve the same effect much more succinctly:
|
We'll start with the most innocuous operation of all: assignment. Then we will look at sequence types in detail.
5.2.1 Assignment
Python's assignment statement operates on values. But what is a value? Consider the following code fragment:
This code shows that when we write word2 = word1 in line ![[1]](callouts/callout1.gif) ,
the value of word1 (the string 'Monty') is assigned to word2.
That is, word2 is a copy of word1, so when we overwrite
word1 with a new string 'Python' in line
,
the value of word1 (the string 'Monty') is assigned to word2.
That is, word2 is a copy of word1, so when we overwrite
word1 with a new string 'Python' in line ![[2]](callouts/callout2.gif) , the value
of word2 is not affected.
, the value
of word2 is not affected.
However, assignment statements do not always involve making copies in this way.
An important subtlety of Python is that the "value" of a structured object
(such as a list) is actually a reference to the object. In the
following example, line ![[1]](callouts/callout1.gif) assigns the reference of list1 to the new variable list2.
When we modify something inside list1 on line
assigns the reference of list1 to the new variable list2.
When we modify something inside list1 on line ![[2]](callouts/callout2.gif) , we can see
that the contents of list2 have also been changed.
, we can see
that the contents of list2 have also been changed.
|
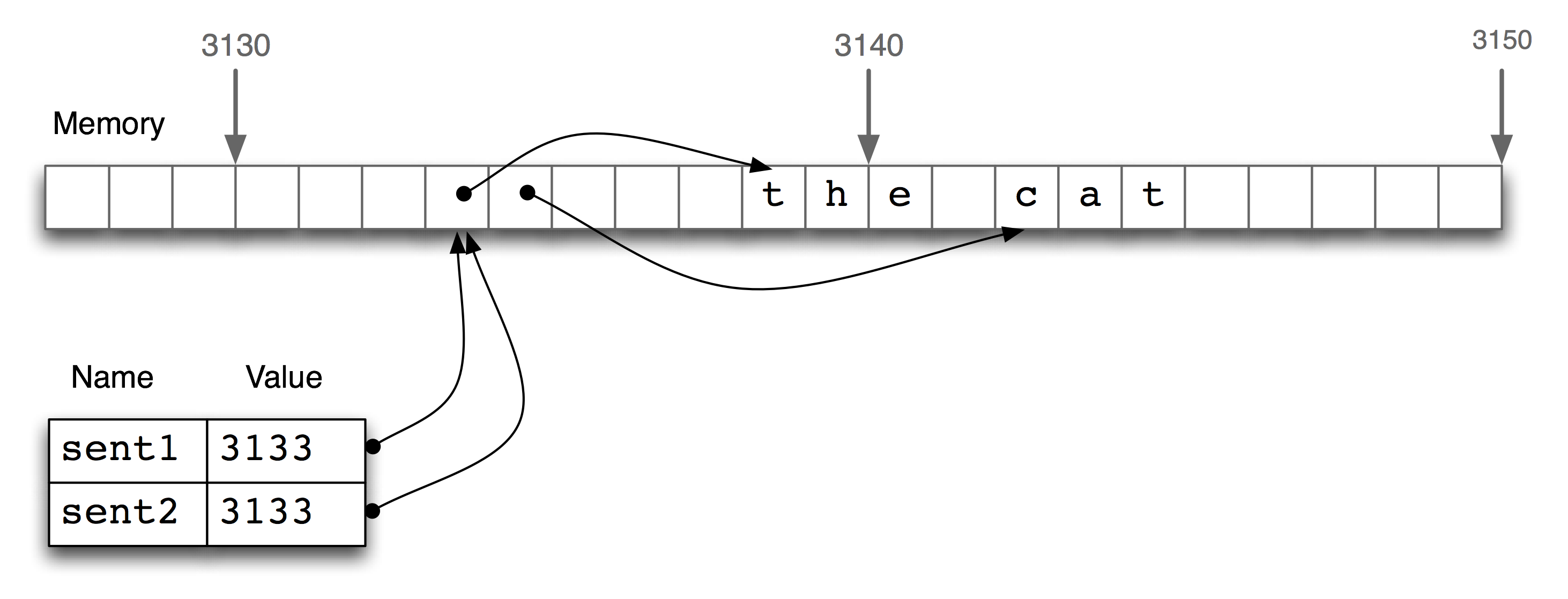
Figure 5.1: List Assignment and Computer Memory
Thus line ![[1]](callouts/callout1.gif) does not copy the contents of the
variable, only its "object reference".
To understand what is going on here, we need to
know how lists are stored in the computer's memory.
In Figure 5.1, we see that a list sent1 is
a reference to an object stored at location 3133 (which is
itself a series of pointers to other locations holding strings).
When we assign sent2 = sent1, it is just the object reference
3133 that gets copied.
does not copy the contents of the
variable, only its "object reference".
To understand what is going on here, we need to
know how lists are stored in the computer's memory.
In Figure 5.1, we see that a list sent1 is
a reference to an object stored at location 3133 (which is
itself a series of pointers to other locations holding strings).
When we assign sent2 = sent1, it is just the object reference
3133 that gets copied.
5.2.2 Sequences: Strings, Lists and Tuples
We have seen three kinds of sequence object: strings, lists, and tuples. As sequences, they have some common properties: they can be indexed and they have a length:
|
We can iterate over the items in a sequence s in a variety of useful ways, as shown in Table 5.1.
| Python Expression | Comment |
|---|---|
| for item in s | iterate over the items of s |
| for item in sorted(s) | iterate over the items of s in order |
| for item in set(s) | iterate over unique elements of s |
| for item in reversed(s) | iterate over elements of s in reverse |
| for item in set(s).difference(t) | iterate over elements of s not in t |
| for item in random.shuffle(s) | iterate over elements of s in random order |
The sequence functions illustrated in Table 5.1 can be combined in various ways; for example, to get unique elements of s sorted in reverse, use reversed(sorted(set(s))).
We can convert between these sequence types. For example, tuple(s) converts any kind of sequence into a tuple, and list(s) converts any kind of sequence into a list. We can convert a list of strings to a single string using the join() function, e.g. ':'.join(words).
Notice in the above code sample that we computed multiple values on a single line, separated by commas. These comma-separated expressions are actually just tuples — Python allows us to omit the parentheses around tuples if there is no ambiguity. When we print a tuple, the parentheses are always displayed. By using tuples in this way, we are implicitly aggregating items together.
In the next example, we use tuples to re-arrange the contents of our list. (We can omit the parentheses because the comma has higher precedence than assignment.)
|
This is an idiomatic and readable way to move items inside a list. It is equivalent to the following traditional way of doing such tasks that does not use tuples (notice that this method needs a temporary variable tmp).
|
As we have seen, Python has sequence functions such as sorted() and reversed() that rearrange the items of a sequence. There are also functions that modify the structure of a sequence and which can be handy for language processing. Thus, zip() takes the items of two sequences and "zips" them together into a single list of pairs. Given a sequence s, enumerate(s) returns an iterator that produces a pair of an index and the item at that index.
|
5.2.3 Combining Different Sequence Types
Let's combine our knowledge of these three sequence types, together with list comprehensions, to perform the task of sorting the words in a string by their length.
Each of the above lines of code contains a significant feature.
Line ![[1]](callouts/callout1.gif) demonstrates that a simple string is actually
an object with methods defined on it, such as split().
Line
demonstrates that a simple string is actually
an object with methods defined on it, such as split().
Line ![[2]](callouts/callout2.gif) shows the construction of a list of tuples,
where each tuple consists of a number (the word length) and the
word, e.g. (3, 'the'). Line
shows the construction of a list of tuples,
where each tuple consists of a number (the word length) and the
word, e.g. (3, 'the'). Line ![[3]](callouts/callout3.gif) sorts the list,
modifying the list in-place. Finally, line
sorts the list,
modifying the list in-place. Finally, line ![[4]](callouts/callout4.gif) discards
the length information then joins the words back into a single string.
discards
the length information then joins the words back into a single string.
We began by talking about the commonalities in these sequence types, but the above code illustrates important differences in their roles. First, strings appear at the beginning and the end: this is typical in the context where our program is reading in some text and producing output for us to read. Lists and tuples are used in the middle, but for different purposes. A list is typically a sequence of objects all having the same type, of arbitrary length. We often use lists to hold sequences of words. In contrast, a tuple is typically a collection of objects of different types, of fixed length. We often use a tuple to hold a record, a collection of different fields relating to some entity. This distinction between the use of lists and tuples takes some getting used to, so here is another example:
|
Here, a lexicon is represented as a list because it is a collection of objects of a single type — lexical entries — of no predetermined length. An individual entry is represented as a tuple because it is a collection of objects with different interpretations, such as the orthographic form, the part of speech, and the pronunciations represented in the SAMPA computer readable phonetic alphabet. Note that these pronunciations are stored using a list. (Why?)
The distinction between lists and tuples has been described in terms of usage. However, there is a more fundamental difference: in Python, lists are mutable, while tuples are immutable. In other words, lists can be modified, while tuples cannot. Here are some of the operations on lists that do in-place modification of the list. None of these operations is permitted on a tuple, a fact you should confirm for yourself.
|
5.2.4 Stacks and Queues
Lists are a particularly versatile data type. We can use lists to implement higher-level data types such as stacks and queues. A stack is a container that has a last-in-first-out policy for adding and removing items (see Figure 5.2).
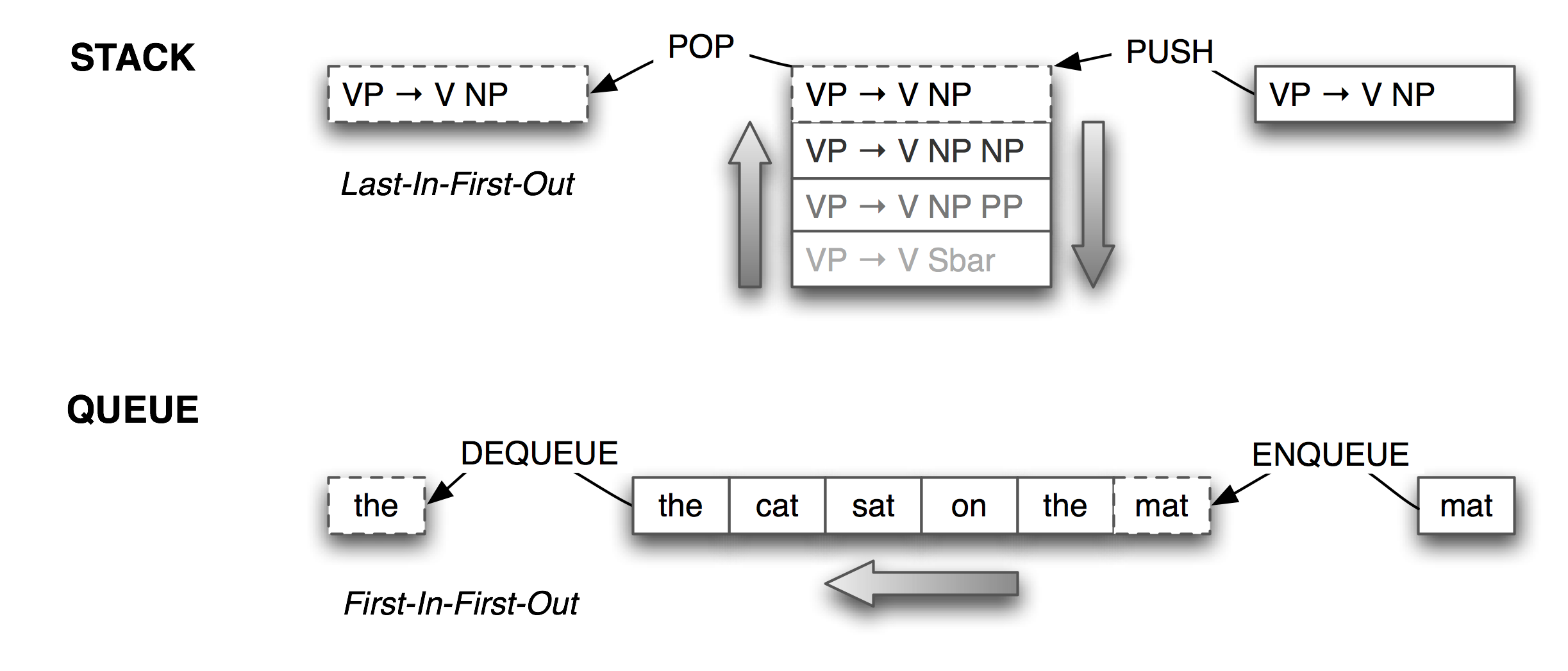
Figure 5.2: Stacks and Queues
Stacks are used to keep track of the current context in computer processing of natural languages (and programming languages too). We will seldom have to deal with stacks explicitly, as the implementation of NLTK parsers, treebank corpus readers, (and even Python functions), all use stacks behind the scenes. However, it is important to understand what stacks are and how they work.
| ||
| ||
Listing 5.1 (check_parens.py): Check parentheses are balanced |
In Python, we can treat a list as a stack by limiting ourselves to the three operations defined on stacks: append(item) (to push item onto the stack), pop() to pop the item off the top of the stack, and [-1] to access the item on the top of the stack. Listing 5.1 processes a sentence with phrase markers, and checks that the parentheses are balanced. The loop pushes material onto the stack when it gets an open parenthesis, and pops the stack when it gets a close parenthesis. We see that two are left on the stack at the end; i.e. the parentheses are not balanced.
Although Listing 5.1 is a useful illustration of stacks, it is overkill because we could have done a direct count: phrase.count('(') == phrase.count(')'). However, we can use stacks for more sophisticated processing of strings containing nested structure, as shown in Listing 5.2. Here we build a (potentially deeply-nested) list of lists. Whenever a token other than a parenthesis is encountered, we add it to a list at the appropriate level of nesting. The stack cleverly keeps track of this level of nesting, exploiting the fact that the item at the top of the stack is actually shared with a more deeply nested item. (Hint: add diagnostic print statements to the function to help you see what it is doing.)
| ||
| ||
Listing 5.2 (convert_parens.py): Convert a nested phrase into a nested list using a stack |
Lists can be used to represent another important data structure. A queue is a container that has a first-in-first-out policy for adding and removing items (see Figure 5.2). Queues are used for scheduling activities or resources. As with stacks, we will seldom have to deal with queues explicitly, as the implementation of NLTK n-gram taggers (Section 3.5.5) and chart parsers (Section 8.2) use queues behind the scenes. However, we will take a brief look at how queues are implemented using lists.
|
5.2.5 More List Comprehensions
You may recall that in Chapter 2, we introduced list comprehensions, with examples like the following:
|
List comprehensions are a convenient and readable way to express list operations in Python, and they have a wide range of uses in natural language processing. In this section we will see some more examples. The first of these takes successive overlapping slices of size n (a sliding window) from a list (pay particular attention to the range of the variable i).
|
You can also use list comprehensions for a kind of multiplication (or cartesian product). Here we generate all combinations of two determiners, two adjectives, and two nouns. The list comprehension is split across three lines for readability.
|
The above example contains three independent for loops. These loops have no variables in common, and we could have put them in any order. We can also have nested loops with shared variables. The next example iterates over all sentences in a section of the Brown Corpus, and for each sentence, iterates over each word.
|
As you will see, the list comprehension in this example contains a final if clause that allows us to filter out any words that fail to meet the specified condition.
Another way to use loop variables is to ignore them! This is
the standard method for building multidimensional structures.
For example, to build an array with m rows and n columns,
where each cell is a set, we would use a nested list comprehension,
as shown in line ![[1]](callouts/callout1.gif) below. Observe that the loop variables
i and j are not used anywhere in the expressions preceding the
for clauses.
below. Observe that the loop variables
i and j are not used anywhere in the expressions preceding the
for clauses.
|
Sometimes we use a list comprehension as part of a larger aggregation task. In the following example we calculate the average length of words in part of the Brown Corpus. Notice that we don't bother storing the list comprehension in a temporary variable, but use it directly as an argument to the average() function.
|
Now that we have reviewed the sequence types, we have one more fundamental data type to revisit.
5.2.6 Dictionaries
As you have already seen, the dictionary data type can be used in a variety of language processing tasks (e.g. Section 1.7). However, we have only scratched the surface. Dictionaries have many more applications than you might have imagined.
Note
The dictionary data type is often known by the name associative array. A normal array maps from integers (the keys) to arbitrary data types (the values), while an associative array places no such constraint on keys. Keys can be strings, tuples, or other more deeply nested structure. Python places the constraint that keys must be immutable.
Let's begin by comparing dictionaries with tuples. Tuples allow access by position; to access the part-of-speech of the following lexical entry we just have to know it is found at index position 1. However, dictionaries allow access by name:
|
In this case, dictionaries are little more than a convenience. We can even simulate access by name using well-chosen constants, e.g.:
|
This method works when there is a closed set of keys and the keys are known in advance. Dictionaries come into their own when we are mapping from an open set of keys, which happens when the keys are drawn from an unrestricted vocabulary or where they are generated by some procedure. Listing 5.3 illustrates the first of these. The function mystery() begins by initializing a dictionary called groups, then populates it with words. We leave it as an exercise for the reader to work out what this function computes. For now, it's enough to note that the keys of this dictionary are an open set, and it would not be feasible to use a integer keys, as would be required if we used lists or tuples for the representation.
| ||
| ||
Listing 5.3 (mystery.py): Mystery program |
Listing 5.3 illustrates two important idioms, which we already
touched on in Chapter 1. First, dictionary keys
are unique; in order to store multiple items in a single entry we
define the value to be a list or a set, and simply update the value each
time we want to store another item (line ![[3]](callouts/callout3.gif) ). Second, if a key does
not yet exist in a dictionary (line
). Second, if a key does
not yet exist in a dictionary (line ![[1]](callouts/callout1.gif) ) we must explicitly add it
and give it an initial value (line
) we must explicitly add it
and give it an initial value (line ![[2]](callouts/callout2.gif) ).
).
The second important use of dictionaries is for mappings that involve compound keys. Suppose we want to categorize a series of linguistic observations according to two or more properties. We can combine the properties using a tuple and build up a dictionary in the usual way, as exemplified in Listing 5.4.
| ||
Listing 5.4 (compound_keys.py): Illustration of compound keys |
5.2.7 Exercises
☼ Find out more about sequence objects using Python's help facility. In the interpreter, type help(str), help(list), and help(tuple). This will give you a full list of the functions supported by each type. Some functions have special names flanked with underscore; as the help documentation shows, each such function corresponds to something more familiar. For example x.__getitem__(y) is just a long-winded way of saying x[y].
☼ Identify three operations that can be performed on both tuples and lists. Identify three list operations that cannot be performed on tuples. Name a context where using a list instead of a tuple generates a Python error.
☼ Find out how to create a tuple consisting of a single item. There are at least two ways to do this.
☼ Create a list words = ['is', 'NLP', 'fun', '?']. Use a series of assignment statements (e.g. words[1] = words[2]) and a temporary variable tmp to transform this list into the list ['NLP', 'is', 'fun', '!']. Now do the same transformation using tuple assignment.
☼ Does the method for creating a sliding window of n-grams behave correctly for the two limiting cases: n = 1, and n = len(sent)?
◑ Create a list of words and store it in a variable sent1. Now assign sent2 = sent1. Modify one of the items in sent1 and verify that sent2 has changed.
- Now try the same exercise but instead assign sent2 = sent1[:]. Modify sent1 again and see what happens to sent2. Explain.
- Now define text1 to be a list of lists of strings (e.g. to represent a text consisting of multiple sentences. Now assign text2 = text1[:], assign a new value to one of the words, e.g. text1[1][1] = 'Monty'. Check what this did to text2. Explain.
- Load Python's deepcopy() function (i.e. from copy import deepcopy), consult its documentation, and test that it makes a fresh copy of any object.
◑ Write code that starts with a string of words and results in a new string consisting of the same words, but where the first word swaps places with the second, and so on. For example, 'the cat sat on the mat' will be converted into 'cat the on sat mat the'.
◑ Initialize an n-by-m list of lists of empty strings using list multiplication, e.g. word_table = [[''] * n] * m. What happens when you set one of its values, e.g. word_table[1][2] = "hello"? Explain why this happens. Now write an expression using range() to construct a list of lists, and show that it does not have this problem.
◑ Write code to initialize a two-dimensional array of sets called word_vowels and process a list of words, adding each word to word_vowels[l][v] where l is the length of the word and v is the number of vowels it contains.
◑ Write code that builds a dictionary of dictionaries of sets.
◑ Use sorted() and set() to get a sorted list of tags used in the Brown corpus, removing duplicates.
◑ Read up on Gematria, a method for assigning numbers to words, and for mapping between words having the same number to discover the hidden meaning of texts (http://en.wikipedia.org/wiki/Gematria, http://essenes.net/gemcal.htm).
Write a function gematria() that sums the numerical values of the letters of a word, according to the letter values in letter_vals:
- letter_vals = {'a':1, 'b':2, 'c':3, 'd':4, 'e':5, 'f':80, 'g':3, 'h':8,
'i':10, 'j':10, 'k':20, 'l':30, 'm':40, 'n':50, 'o':70, 'p':80, 'q':100, 'r':200, 's':300, 't':400, 'u':6, 'v':6, 'w':800, 'x':60, 'y':10, 'z':7}
Use the method from Listing 5.3 to index English words according to their values.
Process a corpus (e.g. nltk.corpus.state_union) and for each document, count how many of its words have the number 666.
Write a function decode() to process a text, randomly replacing words with their Gematria equivalents, in order to discover the "hidden meaning" of the text.
★ Extend the example in Listing 5.4 in the following ways:
- Define two sets verbs and preps, and add each verb and preposition as they are encountered. (Note that you can add an item to a set without bothering to check whether it is already present.)
- Create nested loops to display the results, iterating over verbs and prepositions in sorted order. Generate one line of output per verb, listing prepositions and attachment ratios as follows: raised: about 0:3, at 1:0, by 9:0, for 3:6, from 5:0, in 5:5...
- We used a tuple to represent a compound key consisting of two strings. However, we could have simply concatenated the strings, e.g. key = verb + ":" + prep, resulting in a simple string key. Why is it better to use tuples for compound keys?
5.3 Presenting Results
Often we write a program to report a single datum, such as a particular element in a corpus that meets some complicated criterion, or a single summary statistic such as a word-count or the performance of a tagger. More often, we write a program to produce a structured result, such as a tabulation of numbers or linguistic forms, or a reformatting of the original data. When the results to be presented are linguistic, textual output is usually the most natural choice. However, when the results are numerical, it may be preferable to produce graphical output. In this section you will learn about a variety of ways to present program output.
5.3.1 Strings and Formats
We have seen that there are two ways to display the contents of an object:
|
The print command yields Python's attempt to produce the most human-readable form of an object. The second method — naming the variable at a prompt — shows us a string that can be used to recreate this object. It is important to keep in mind that both of these are just strings, displayed for the benefit of you, the user. They do not give us any clue as to the actual internal representation of the object.
There are many other useful ways to display an object as a string of characters. This may be for the benefit of a human reader, or because we want to export our data to a particular file format for use in an external program.
Formatted output typically contains a combination of variables and pre-specified strings, e.g. given a dictionary wordcount consisting of words and their frequencies we could do:
|
Apart from the problem of unwanted whitespace, print statements that contain alternating variables and constants can be difficult to read and maintain. A better solution is to use formatting strings:
|
5.3.2 Lining Things Up
So far our formatting strings have contained specifications of fixed width, such as %6s, a string that is padded to width 6 and right-justified. We can include a minus sign to make it left-justified. In case we don't know in advance how wide a displayed value should be, the width value can be replaced with a star in the formatting string, then specified using a variable:
|
Other control characters are used for decimal integers and floating point numbers. Since the percent character % has a special interpretation in formatting strings, we have to precede it with another % to get it in the output:
|
An important use of formatting strings is for tabulating data.
The program in Listing 5.5 iterates over five genres of the Brown Corpus.
For each token having the md tag we increment a count. To do this we
have used ConditionalFreqDist(), where the condition is the current genre
and the event is the modal, i.e. this constructs a frequency distribution of
the modal verbs in each genre.
Line ![[1]](callouts/callout1.gif) identifies a small set of modals of interest, and calls
the function tabulate() that
processes the data structure to output the required counts.
Note that we have been careful to separate the language processing
from the tabulation of results.
identifies a small set of modals of interest, and calls
the function tabulate() that
processes the data structure to output the required counts.
Note that we have been careful to separate the language processing
from the tabulation of results.
| ||
| ||
Listing 5.5 (modal_tabulate.py): Frequency of Modals in Different Sections of the Brown Corpus |
There are some interesting patterns in the table produced by Listing 5.5. For instance, compare row d (government literature) with row n (adventure literature); the former is dominated by the use of can, may, must, will while the latter is characterized by the use of could and might. With some further work it might be possible to guess the genre of a new text automatically, simply using information about the distribution of modal verbs.
Our next example, in Listing 5.6, generates a concordance display. We use the left/right justification of strings and the variable width to get vertical alignment of a variable-width window.
[TODO: explain ValueError exception]
| ||
| ||
Listing 5.6 (concordance.py): Simple Concordance Display |
5.3.3 Writing Results to a File
We have seen how to read text from files (Section 2.2.1). It is often useful to write output to files as well. The following code opens a file output.txt for writing, and saves the program output to the file.
|
When we write non-text data to a file we must convert it to a string first. We can do this conversion using formatting strings, as we saw above. We can also do it using Python's backquote notation, which converts any object into a string. Let's write the total number of words to our file, before closing it.
|
5.3.4 Graphical Presentation
So far we have focused on textual presentation and the use of formatted print statements to get output lined up in columns. It is often very useful to display numerical data in graphical form, since this often makes it easier to detect patterns. For example, in Listing 5.5 we saw a table of numbers showing the frequency of particular modal verbs in the Brown Corpus, classified by genre. In Listing 5.7 we present the same information in graphical format. The output is shown in Figure 5.3 (a color figure in the online version).
Note
Listing 5.7 uses the PyLab package which supports sophisticated plotting functions with a MATLAB-style interface. For more information about this package please see http://matplotlib.sourceforge.net/.
| ||
| ||
Listing 5.7 (modal_plot.py): Frequency of Modals in Different Sections of the Brown Corpus |
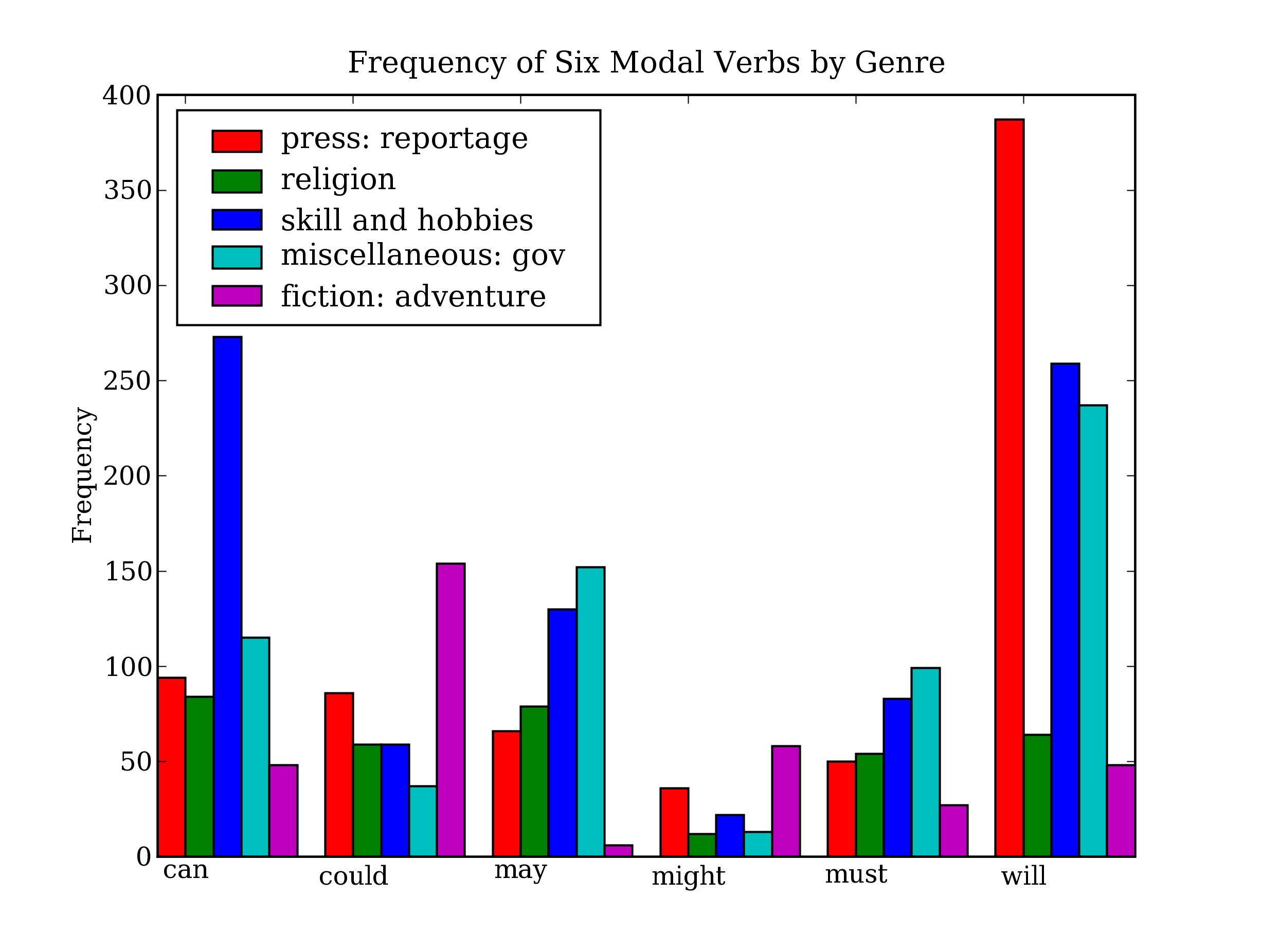
Figure 5.3: Bar Chart Showing Frequency of Modals in Different Sections of Brown Corpus
From the bar chart it is immediately obvious that may and must have almost identical relative frequencies. The same goes for could and might.
5.3.5 Exercises
- ☼ Write code that removes whitespace at the beginning and end of a
string, and normalizes whitespace between words to be a single
space character.
- do this task using split() and join()
- do this task using regular expression substitutions
- ☼ What happens when the formatting strings %6s and %-6s are used to display strings that are longer than six characters?
- ☼ We can use a dictionary to specify the values to be substituted into a formatting string. Read Python's library documentation for formatting strings (http://docs.python.org/lib/typesseq-strings.html), and use this method to display today's date in two different formats.
- ◑ Listing 3.3 in Chapter 3 plotted a curve showing change in the performance of a lookup tagger as the model size was increased. Plot the performance curve for a unigram tagger, as the amount of training data is varied.
5.4 Functions
Once you have been programming for a while, you will find that you need to perform a task that you have done in the past. In fact, over time, the number of completely novel things you have to do in creating a program decreases significantly. Half of the work may involve simple tasks that you have done before. Thus it is important for your code to be re-usable. One effective way to do this is to abstract commonly used sequences of steps into a function, as we briefly saw in Chapter 1.
For example, suppose we find that we often want to read text from an HTML file. This involves several steps: opening the file, reading it in, normalizing whitespace, and stripping HTML markup. We can collect these steps into a function, and give it a name such as get_text():
| ||
Listing 5.8 (get_text.py): Read text from a file |
Now, any time we want to get cleaned-up text from an HTML file, we can just call get_text() with the name of the file as its only argument. It will return a string, and we can assign this to a variable, e.g.: contents = get_text("test.html"). Each time we want to use this series of steps we only have to call the function.
Notice that a function definition consists of the keyword def (short for "define"), followed by the function name, followed by a sequence of parameters enclosed in parentheses, then a colon. The following lines contain an indented block of code, the function body.
Using functions has the benefit of saving space in our program. More importantly, our choice of name for the function helps make the program readable. In the case of the above example, whenever our program needs to read cleaned-up text from a file we don't have to clutter the program with four lines of code, we simply need to call get_text(). This naming helps to provide some "semantic interpretation" — it helps a reader of our program to see what the program "means".
Notice that the above function definition contains a string. The first string inside a function definition is called a docstring. Not only does it document the purpose of the function to someone reading the code, it is accessible to a programmer who has loaded the code from a file:
- get_text(file)
- Read text from a file, normalizing whitespace and stripping HTML markup.
We have seen that functions help to make our work reusable and readable. They also help make it reliable. When we re-use code that has already been developed and tested, we can be more confident that it handles a variety of cases correctly. We also remove the risk that we forget some important step, or introduce a bug. The program that calls our function also has increased reliability. The author of that program is dealing with a shorter program, and its components behave transparently.
- [More: overview of section]
5.4.1 Function Arguments
- multiple arguments
- named arguments
- default values
Python is a dynamically typed language. It does not force us to declare the type of a variable when we write a program. This feature is often useful, as it permits us to define functions that are flexible about the type of their arguments. For example, a tagger might expect a sequence of words, but it wouldn't care whether this sequence is expressed as a list, a tuple, or an iterator.
However, often we want to write programs for later use by others, and want to program in a defensive style, providing useful warnings when functions have not been invoked correctly. Observe that the tag() function in Listing 5.9 behaves sensibly for string arguments, but that it does not complain when it is passed a dictionary.
| ||
| ||
Listing 5.9 (tag1.py): A tagger that tags anything |
It would be helpful if the author of this function took some extra steps to ensure that the word parameter of the tag() function is a string. A naive approach would be to check the type of the argument and return a diagnostic value, such as Python's special empty value, None, as shown in Listing 5.10.
| ||
Listing 5.10 (tag2.py): A tagger that only tags strings |
However, this approach is dangerous because the calling program may not detect the error, and the diagnostic return value may be propagated to later parts of the program with unpredictable consequences. A better solution is shown in Listing 5.11.
| ||
Listing 5.11 (tag3.py): A tagger that generates an error message when not passed a string |
This produces an error that cannot be ignored, since it halts program execution. Additionally, the error message is easy to interpret. (We will see an even better approach, known as "duck typing" in Chapter 9.)
Another aspect of defensive programming concerns the return statement of a function. In order to be confident that all execution paths through a function lead to a return statement, it is best to have a single return statement at the end of the function definition. This approach has a further benefit: it makes it more likely that the function will only return a single type. Thus, the following version of our tag() function is safer:
|
A return statement can be used to pass multiple values back to the calling program, by packing them into a tuple. Here we define a function that returns a tuple consisting of the average word length of a sentence, and the inventory of letters used in the sentence. It would have been clearer to write two separate functions.
|
Functions do not need to have a return statement at all. Some functions do their work as a side effect, printing a result, modifying a file, or updating the contents of a parameter to the function. Consider the following three sort functions; the last approach is dangerous because a programmer could use it without realizing that it had modified its input.
|
5.4.2 An Important Subtlety
Back in Section 5.2.1 you saw that in Python, assignment works on values, but that the value of a structured object is a reference to that object. The same is true for functions. Python interprets function parameters as values (this is known as call-by-value). Consider Listing 5.12. Function set_up() has two parameters, both of which are modified inside the function. We begin by assigning an empty string to w and an empty dictionary to p. After calling the function, w is unchanged, while p is changed:
| ||
| ||
To understand why w was not changed, it is necessary to understand call-by-value. When we called set_up(w, p), the value of w (an empty string) was assigned to a new variable word. Inside the function, the value of word was modified. However, that had no effect on the external value of w. This parameter passing is identical to the following sequence of assignments:
|
In the case of the structured object, matters are quite different. When we called set_up(w, p), the value of p (an empty dictionary) was assigned to a new local variable properties. Since the value of p is an object reference, both variables now reference the same memory location. Modifying something inside properties will also change p, just as if we had done the following sequence of assignments:
|
Thus, to understand Python's call-by-value parameter passing, it is enough to understand Python's assignment operation. We will address some closely related issues in our later discussion of variable scope (Section 9).
5.4.3 Functional Decomposition
Well-structured programs usually make extensive use of functions. When a block of program code grows longer than 10-20 lines, it is a great help to readability if the code is broken up into one or more functions, each one having a clear purpose. This is analogous to the way a good essay is divided into paragraphs, each expressing one main idea.
Functions provide an important kind of abstraction. They allow us to group multiple actions into a single, complex action, and associate a name with it. (Compare this with the way we combine the actions of go and bring back into a single more complex action fetch.) When we use functions, the main program can be written at a higher level of abstraction, making its structure transparent, e.g.
|
Appropriate use of functions makes programs more readable and maintainable. Additionally, it becomes possible to reimplement a function — replacing the function's body with more efficient code — without having to be concerned with the rest of the program.
Consider the freq_words function in Listing 5.13. It updates the contents of a frequency distribution that is passed in as a parameter, and it also prints a list of the n most frequent words.
| ||
| ||
This function has a number of problems. The function has two side-effects: it modifies the contents of its second parameter, and it prints a selection of the results it has computed. The function would be easier to understand and to reuse elsewhere if we initialize the FreqDist() object inside the function (in the same place it is populated), and if we moved the selection and display of results to the calling program. In Listing 5.14 we refactor this function, and simplify its interface by providing a single url parameter.
| ||
| ||
Note that we have now simplified the work of freq_words to the point that we can do its work with three lines of code:
|
5.4.4 Documentation (notes)
- some guidelines for literate programming (e.g. variable and function naming)
- documenting functions (user-level and developer-level documentation)
5.4.5 Functions as Arguments
So far the arguments we have passed into functions have been simple objects like strings, or structured objects like lists. These arguments allow us to parameterize the behavior of a function. As a result, functions are very flexible and powerful abstractions, permitting us to repeatedly apply the same operation on different data. Python also lets us pass a function as an argument to another function. Now we can abstract out the operation, and apply a different operation on the same data. As the following examples show, we can pass the built-in function len() or a user-defined function last_letter() as parameters to another function:
|
Surprisingly, len and last_letter are objects that can be passed around like lists and dictionaries. Notice that parentheses are only used after a function name if we are invoking the function; when we are simply passing the function around as an object these are not used.
Python provides us with one more way to define functions as arguments to other functions, so-called lambda expressions. Supposing there was no need to use the above last_letter() function in multiple places, and thus no need to give it a name. We can equivalently write the following:
|
Our next example illustrates passing a function to the sorted() function. When we call the latter with a single argument (the list to be sorted), it uses the built-in lexicographic comparison function cmp(). However, we can supply our own sort function, e.g. to sort by decreasing length.
|
In 5.2.5 we saw an example of filtering out some items in a list comprehension, using an if test. Similarly, we can restrict a list to just the lexical words, using [word for word in sent if is_lexical(word)]. This is a little cumbersome as it mentions the word variable three times. A more compact way to express the same thing is as follows.
|
The function is_lexical(word) returns True just in case word, when normalized to lowercase, is not in the given list. This function is itself used as an argument to filter(). The filter() function applies its first argument (a function) to each item of its second (a sequence), only passing it through if the function returns true for that item. Thus filter(f, seq) is equivalent to [item for item in seq if apply(f,item) == True].
Another helpful function, which like filter() applies a function to a sequence, is map(). Here is a simple way to find the average length of a sentence in a section of the Brown Corpus:
|
Instead of len(), we could have passed in any other function we liked:
|
Instead of using filter() to call a named function is_vowel, we can define a lambda expression as follows:
|
5.4.6 Exercises
- ☼ Review the answers that you gave for the exercises in 5.2, and rewrite the code as one or more functions.
- ◑ In this section we saw examples of some special functions such as filter() and map(). Other functions in this family are zip() and reduce(). Find out what these do, and write some code to try them out. What uses might they have in language processing?
- ◑ Write a function that takes a list of words (containing duplicates) and returns a list of words (with no duplicates) sorted by decreasing frequency. E.g. if the input list contained 10 instances of the word table and 9 instances of the word chair, then table would appear before chair in the output list.
- ◑ Write a function that takes a text and a vocabulary as its arguments and returns the set of words that appear in the text but not in the vocabulary. Both arguments can be represented as lists of strings. Can you do this in a single line, using set.difference()?
- ◑ As you saw, zip() combines two lists into a single list of pairs. What happens when the lists are of unequal lengths? Define a function myzip() that does something different with unequal lists.
- ◑ Import the itemgetter() function from the operator module in Python's standard library (i.e. from operator import itemgetter). Create a list words containing several words. Now try calling: sorted(words, key=itemgetter(1)), and sorted(words, key=itemgetter(-1)). Explain what itemgetter() is doing.
5.5 Algorithm Design Strategies
A major part of algorithmic problem solving is selecting or adapting an appropriate algorithm for the problem at hand. Whole books are written on this topic (e.g. [Levitin, 2004]) and we only have space to introduce some key concepts and elaborate on the approaches that are most prevalent in natural language processing.
The best known strategy is known as divide-and-conquer. We attack a problem of size n by dividing it into two problems of size n/2, solve these problems, and combine their results into a solution of the original problem. Figure 5.4 illustrates this approach for sorting a list of words.
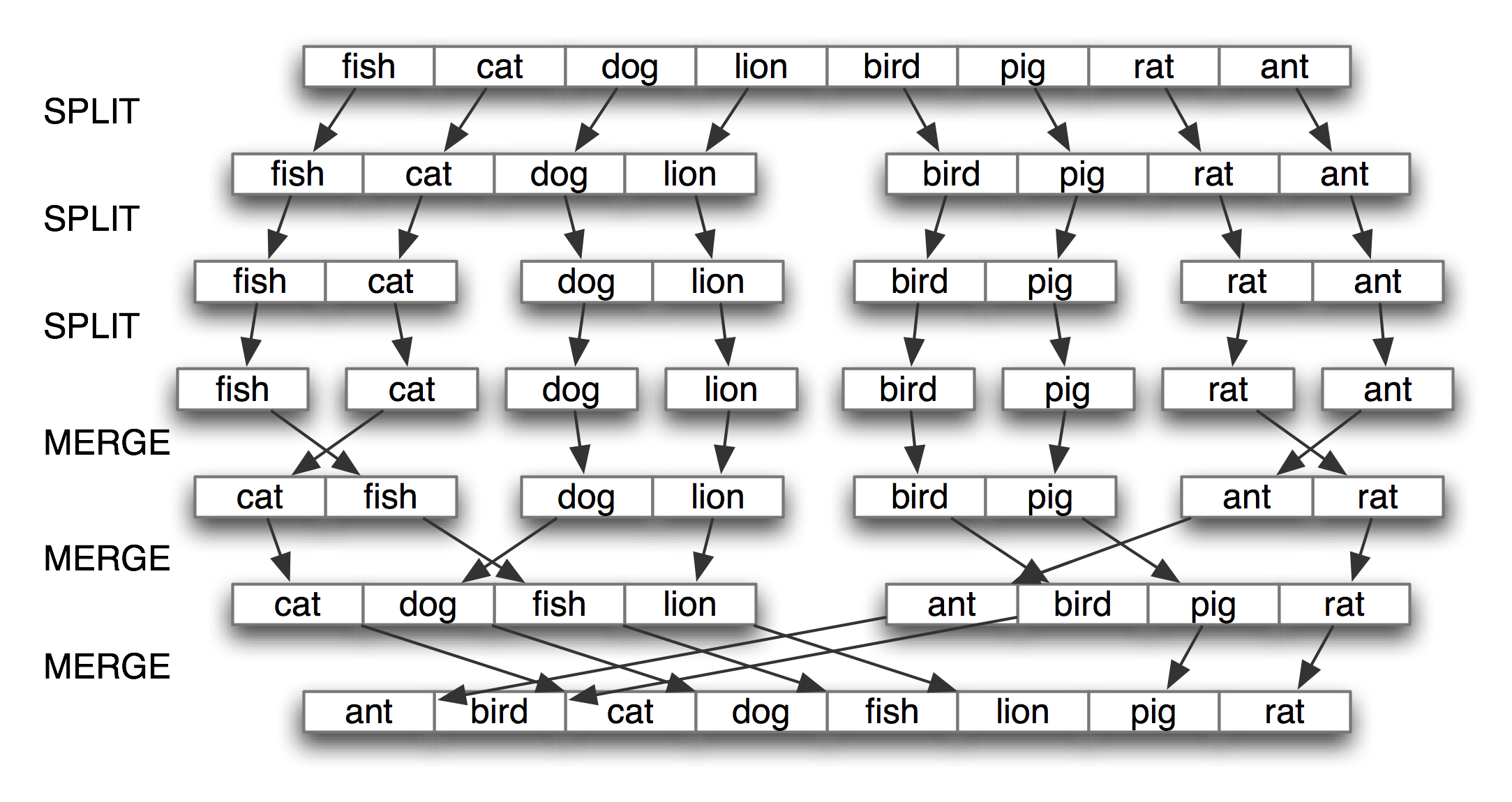
Figure 5.4: Sorting by Divide-and-Conquer (Mergesort)
Another strategy is decrease-and-conquer. In this approach, a small amount of work on a problem of size n permits us to reduce it to a problem of size n/2. Figure 5.5 illustrates this approach for the problem of finding the index of an item in a sorted list.
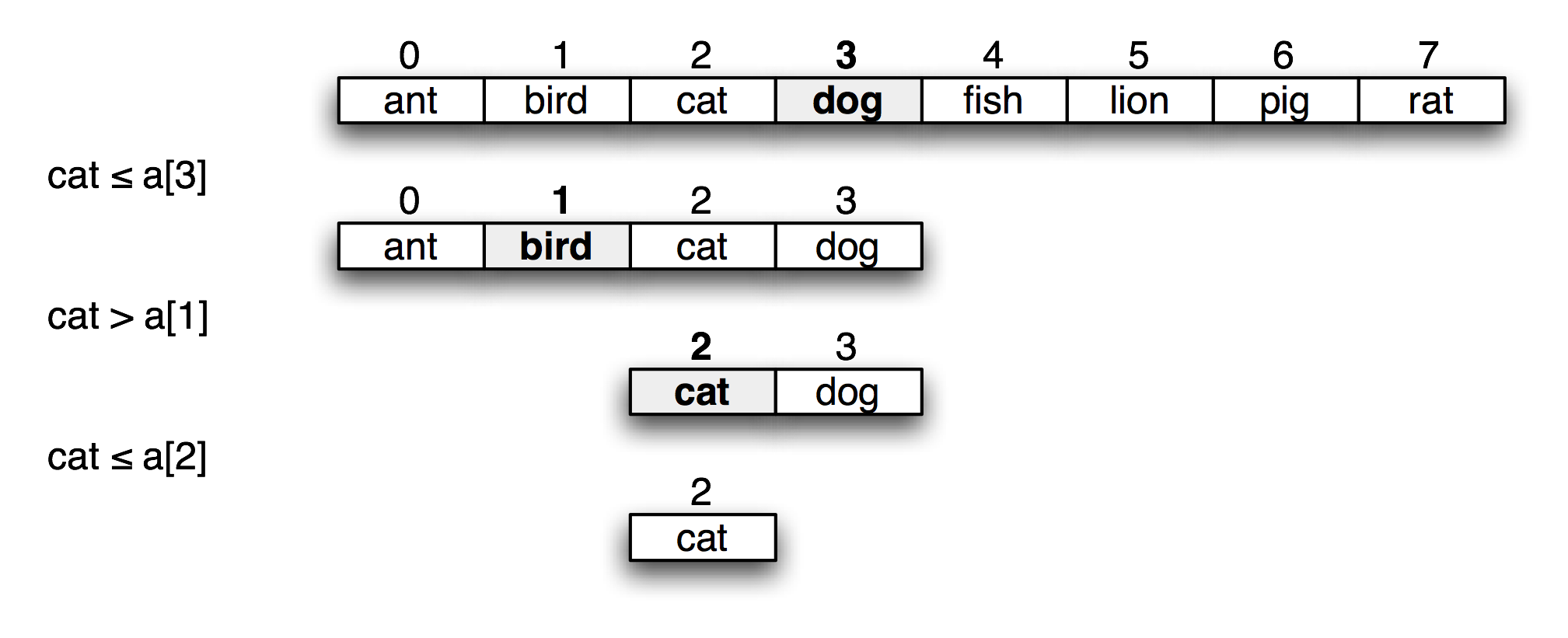
Figure 5.5: Searching by Decrease-and-Conquer (Binary Search)
A third well-known strategy is transform-and-conquer. We attack a problem by transforming it into an instance of a problem we already know how to solve. For example, in order to detect duplicates entries in a list, we can pre-sort the list, then look for adjacent identical items, as shown in Listing 5.15. Our approach to n-gram chunking in Section 6.5 is another case of transform and conquer (why?).
| ||
| ||
Listing 5.15 (presorting.py): Presorting a list for duplicate detection |
5.5.1 Recursion (notes)
We first saw recursion in Chapter 2, in a function that navigated the hypernym hierarchy of WordNet...
Iterative solution:
|
Recursive solution (base case, induction step)
|
[Simple example of recursion on strings.]
Generating all permutations of words, to check which ones are grammatical:
|
5.5.2 Deeply Nested Objects (notes)
We can use recursive functions to build deeply-nested objects. Building a letter trie, Listing 5.16.
| ||
| ||
Listing 5.16 (trie.py): Building a Letter Trie |
5.5.3 Dynamic Programming
Dynamic programming is a general technique for designing algorithms which is widely used in natural language processing. The term 'programming' is used in a different sense to what you might expect, to mean planning or scheduling. Dynamic programming is used when a problem contains overlapping sub-problems. Instead of computing solutions to these sub-problems repeatedly, we simply store them in a lookup table. In the remainder of this section we will introduce dynamic programming, but in a rather different context to syntactic parsing.
Pingala was an Indian author who lived around the 5th century B.C., and wrote a treatise on Sanskrit prosody called the Chandas Shastra. Virahanka extended this work around the 6th century A.D., studying the number of ways of combining short and long syllables to create a meter of length n. He found, for example, that there are five ways to construct a meter of length 4: V4 = {LL, SSL, SLS, LSS, SSSS}. Observe that we can split V4 into two subsets, those starting with L and those starting with S, as shown in (1).
| (1) |
V4 =
LL, LSS
i.e. L prefixed to each item of V2 = {L, SS}
SSL, SLS, SSSS
i.e. S prefixed to each item of V3 = {SL, LS, SSS}
|
| ||
| ||
Listing 5.17 (virahanka.py): Three Ways to Compute Sanskrit Meter |
With this observation, we can write a little recursive function called virahanka1() to compute these meters, shown in Listing 5.17. Notice that, in order to compute V4 we first compute V3 and V2. But to compute V3, we need to first compute V2 and V1. This call structure is depicted in (2).
| (2) | 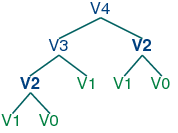 |
As you can see, V2 is computed twice. This might not seem like a significant problem, but it turns out to be rather wasteful as n gets large: to compute V20 using this recursive technique, we would compute V2 4,181 times; and for V40 we would compute V2 63,245,986 times! A much better alternative is to store the value of V2 in a table and look it up whenever we need it. The same goes for other values, such as V3 and so on. Function virahanka2() implements a dynamic programming approach to the problem. It works by filling up a table (called lookup) with solutions to all smaller instances of the problem, stopping as soon as we reach the value we're interested in. At this point we read off the value and return it. Crucially, each sub-problem is only ever solved once.
Notice that the approach taken in virahanka2() is to solve smaller problems on the way to solving larger problems. Accordingly, this is known as the bottom-up approach to dynamic programming. Unfortunately it turns out to be quite wasteful for some applications, since it may compute solutions to sub-problems that are never required for solving the main problem. This wasted computation can be avoided using the top-down approach to dynamic programming, which is illustrated in the function virahanka3() in Listing 5.17. Unlike the bottom-up approach, this approach is recursive. It avoids the huge wastage of virahanka1() by checking whether it has previously stored the result. If not, it computes the result recursively and stores it in the table. The last step is to return the stored result. The final method is to use a Python decorator called memoize, which takes care of the housekeeping work done by virahanka3() without cluttering up the program.
This concludes our brief introduction to dynamic programming. We will encounter it again in Chapter 8.
5.5.4 Timing (notes)
We can easily test the efficiency gains made by the use of dynamic programming, or any other putative performance enhancement, using the timeit module:
|
[MORE]
5.5.5 Exercises
◑ Write a recursive function lookup(trie, key) that looks up a key in a trie, and returns the value it finds. Extend the function to return a word when it is uniquely determined by its prefix (e.g. vanguard is the only word that starts with vang-, so lookup(trie, 'vang') should return the same thing as lookup(trie, 'vanguard')).
◑ Read about string edit distance and the Levenshtein Algorithm. Try the implementation provided in nltk.edit_dist(). How is this using dynamic programming? Does it use the bottom-up or top-down approach? [See also http://norvig.com/spell-correct.html]
◑ The Catalan numbers arise in many applications of combinatorial mathematics, including the counting of parse trees (Chapter 8). The series can be defined as follows: C0 = 1, and Cn+1 = Σ0..n (CiCn-i).
- Write a recursive function to compute nth Catalan number Cn
- Now write another function that does this computation using dynamic programming
- Use the timeit module to compare the performance of these functions as n increases.
★ Write a recursive function that pretty prints a trie in alphabetically sorted order, as follows
chat: 'cat' --ien: 'dog' -???: ???
★ Write a recursive function that processes text, locating the uniqueness point in each word, and discarding the remainder of each word. How much compression does this give? How readable is the resulting text?
5.6 Conclusion
[TO DO]
5.7 Further Reading
http://docs.python.org/lib/typesseq-strings.html
About this document...
This chapter is a draft from Natural Language Processing [http://nltk.org/book.html], by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2008 the authors. It is distributed with the Natural Language Toolkit [http://nltk.org/], Version 0.9.5, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document is