Theorem bj-denotes 32858

Description: This would be the justification for the definition of the unary predicate "E!" by |- ( E! A <-> E. x x = A ) which could be interpreted as " A exists" or " A denotes". It is interesting that this justification can be proved without ax-ext 2602 nor df-cleq 2615 (but of course using df-clab 2609 and df-clel 2618). Once extensionality is postulated, then isset 3207 will prove that "existing" (as a set) is equivalent to being a member of a class.

Note that there is no dv condition on x , y but the theorem does not depend on ax-13 2246. Actually, the proof depends only on ax-1--7 and sp 2053.

The symbol "E!" was chosen to be reminiscent of the analogous predicate in (inclusive or non-inclusive) free logic, which deals with the possibility of non-existent objects. This analogy should not be taken too far, since here there are no equality axioms for classes: they are derived from ax-ext 2602 (e.g., eqid 2622). In particular, one cannot even prove |- E. x x = A => |- A = A.

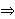With ax-ext 2602, the present theorem is obvious from cbvexv 2275 and eqeq1 2626 (in free logic, the same proof holds since one has equality axioms for terms). (Contributed by BJ, 29-Apr-2019.) (Proof modification is discouraged.)

Assertion

Ref	Expression
bj-denotes	|- ( E. x x = A <-> E. y y = A )

Distinct variable groups:   x, A   y, A

Proof of Theorem bj-denotes

Dummy variable z is distinct from all other variables.

Step	Hyp	Ref	Expression
1		id 22	. . . . . 6 |- ( z = z -> z = z )
2	1	bj-vexwv 32857	. . . . 5 |- x e. { z | ( z = z -> z = z ) }
3	2	biantru 526	. . . 4 |- ( x = A <-> ( x = A /\ x e. { z | ( z = z -> z = z ) } ) )
4	3	exbii 1774	. . 3 |- ( E. x x = A <-> E. x ( x = A /\ x e. { z | ( z = z -> z = z ) } ) )
5		df-clel 2618	. . 3 |- ( A e. { z | ( z = z -> z = z ) } <-> E. x ( x = A /\ x e. { z | ( z = z -> z = z ) } ) )
6		df-clel 2618	. . 3 |- ( A e. { z | ( z = z -> z = z ) } <-> E. y ( y = A /\ y e. { z | ( z = z -> z = z ) } ) )
7	4, 5, 6	3bitr2i 288	. 2 |- ( E. x x = A <-> E. y ( y = A /\ y e. { z | ( z = z -> z = z ) } ) )
8	1	bj-vexwv 32857	. . . . 5 |- y e. { z | ( z = z -> z = z ) }
9	8	biantru 526	. . . 4 |- ( y = A <-> ( y = A /\ y e. { z | ( z = z -> z = z ) } ) )
10	9	bicomi 214	. . 3 |- ( ( y = A /\ y e. { z | ( z = z -> z = z ) } ) <-> y = A )
11	10	exbii 1774	. 2 |- ( E. y ( y = A /\ y e. { z | ( z = z -> z = z ) } ) <-> E. y y = A )
12	7, 11	bitri 264	1 |- ( E. x x = A <-> E. y y = A )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   E.wex 1704   e. wcel 1990   {cab 2608

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-12 2047

This theorem depends on definitions:  df-bi 197  df-an 386  df-ex 1705  df-sb 1881  df-clab 2609  df-clel 2618

This theorem is referenced by:  bj-issetwt  32859  bj-elisset  32862  bj-vtoclg1f1  32910